Introducción
En los últimos años, los cursos de Ingeniería vienen ganando más espacio en el escenario académico brasileño referentes a la formación de recursos humanos para el desarrollo profesional para el mercado de trabajo. Este interés ocurre por diversos factores, entre ellos la perspectiva de ascenso en la carrera y el status social proporcional al público discente (Vargas, 2010). Además de esto, el aumento de la elección de las carreras y las dificultades en el proceso de enseñanza y aprendizaje también crecen.
Estas dificultades, generalmente ocurren en mayor escala durante los primeros años de la carrera, una vez que hay una carga grande de asignaturas relacionadas al núcleo común del área de Física, Química y Matemáticas (Vitelli, 2012). En las matemáticas, hay diferentes componentes curriculares que integran la matriz de los cursos – Álgebra, Cálculo Diferencial e Integral, Ecuaciones Diferenciales, Geometría Analítica, entre otras. De este modo, este trabajo tendrá una discusión especial el aprendizaje de Cálculo Diferencial e Integral I, ya que es una de las asignaturas que tiene los mayores índices de reprobación y deserción en las carreras de ingenierías en los primeros años (Santos, 2014).
El aprendizaje del estudiante en la asignatura de Cálculo Diferencial e Integral I es una de las preocupaciones en el área de Educación Matemática en la Enseñanza Superior, porque sirve de conocimiento elemental para asignaturas más avanzadas en algunas carreras de Ciencias Sociales y Aplicadas, Ciencias Exactas e Ingenierías, como por ejemplo Ecuaciones Diferenciales, Electromagnetismo, Investigación Operacional, entre otras (Barufi, 1999; Gonçalves, 2012).
En el área de Ciencias Sociales y Aplicadas, destaca la carrera de Administración y Economía, en el campo de las Ciencias Exactas, destaca la carrera de Física, Matemática, Química, Ciencia de la Computación, entre otras. Finalmente, en los cursos de Ingeniería, destaca las especialidades de Ambiental, Civil, Computación Producción, Química, Telecomunicaciones – estas son ofrecidas en el lócus de investigación. Es importante mencionar que para que este conocimiento se fortalezca en el aula requiere que el estudiante retome aprendizajes previos de Matemática Elemental aprendidos en la universidad y/o en la Educación Básica, tales como, álgebra, trigonometría, aritmética y geometría (Barufi, 1999; Mosca, León y Rubio, 2012).
Santos (2014) argumenta que los estudiantes que estudian en el periodo nocturno (trabajadores o no), en general, no tienen la habito de estudiar fuera de la clase; es decir; que algunos de ellos no buscan otras formas de estudio y si lo hacen dedican poco tiempo al estudio de la asignaturas de Cálculo I.
Es importante mencionar que situaciones como las que se mencionan con antelación, son una de las principales causas del bajo rendimiento académico de los chavos en Cálculo I, así como la falta de base elementar del conocimiento matemático, como lo argumentan otros autores (Barufi, 1999; Pereira, 2009). Por ello, las problemáticas en el aprendizaje discente en Cálculo Diferencial e Integral I van más allá del espacio universitario, siendo reflejado por una cuestión formativa de la Educación Básica y de los aspectos sociales, como el trabajo, por ejemplo (Cavasotto, 2010). En este artículo se presentarán de una manera breve, la metodología del estudio, el análisis de datos y las discusiones de los resultados, así como las consideraciones finales y referencias.
Metodología
Las reflexiones presentadas son producto de una investigación cuantitativa con enfoque de Estudio de Caso, cuyo objetivo fue analizar el rendimiento académico de los estudiantes en la asignatura de Cálculo Diferencial e Integral I (CDI I), ofrecida en el segundo semestre lectivo de 2013, en los cursos de Ingeniería – Ambiental, Civil, Computación, Producción, Química y Telecomunicaciones – curso impartido en una Institución de Enseñanza Superior Comunitaria situada en la Región Metropolitana de Porto Alegre (Rio Grande do Sul/Brasil).
May (2004), afirma que el estudio de caso es un procedimiento técnico que consiste en analizar solamente un sujeto, grupo, institución, ciudad, entre otros, que correspondan a las mismas características que se define como centrales para la investigación.
El contexto de la investigación fue una Institución de Enseñanza Superior (IES) privada comunitaria brasileña situada en una ciudad cercana a la capital Porto Alegre del Estado del Rio Grande do Sul, región sur de Brasil. La elección de esta IES ocurrió por conveniencia para los investigadores, por la facilidad para la obtención de los datos y realización del trabajo de campo donde se va a desarrollar la investigación (Marconi y Lakatos, 2009).
Los sujetos de investigación fueron 35 estudiantes de un grupo de licenciatura mixto de carreras de Ingeniería – ya mencionadas arriba –, siendo ocho del sexo femenino y 27 del sexo masculino, situados, en general, las edades fluctúan entre los 18 a los 24 años de edad, todos estudiantes de una IES privada y comunitaria.
La recopilación de datos fue realizada a través de una encuesta para la caracterización de los estudiantes y del análisis del rendimiento de los alumnos, en términos de calificaciones obtenidas, contenidas en los registros académicos, teniendo como referencia analítica la estadística descriptiva.
Según Gil (2012), la encuesta es un instrumento de investigación muy práctica y eficiente para el área científico, una vez que por medio de ella se puede recopilar los datos de forma rápida y así analizar las informaciones de modo más profundo.
De acuerdo con Creswell (2010), el uso del abordaje cuantitativo se refiere a la utilización de métodos matemáticos y estadísticos para representar los datos y hacer comprensiones y significaciones sobre los factos y fenómenos analizados, en este caso el desempeño en CDI I, en cuanto al objetivo descriptivo, Both, Colomb y Williams (2010) sustentan que debe centralizase en hacer descripciones sobre el objeto de estudio, que para esta investigación es el rendimiento académico alo largo del segundo semestre de 2013.
Para la recopilación de datos se utilizó las información socio demográfica de los estudiantes (sexo, edad, periodo académico, carrera) y la lista de calificaciones proporcionada por los académicos al final del curso. La información proporcionada por los estudiantes está inserta en las respuestas de las encuestas aplicadas in loco (Santos, 2014) y las calificaciones corresponden a los exámenes del primer y según grados del semestre. Posteriormente, se analizó el desempeño del cuerpo discente en los trabajos y evaluaciones enfatizando que los estudiantes serán denominados por AX siendo A referente a alumnos y X correspondiendo al orden de la respuesta.
Los exámenes de primer grado, denominado G1, consisten en un trabajo en equipo y una prueba individual sin consultar referentes a los contenidos de la primera parte del semestre, es decir, asuntos relacionados a las derivadas en funciones reales de una variable, técnicas de derivación y sus aplicaciones en situaciones-problema. Ya los exámenes de segundo grado, llamado de G2, se refieren a un trabajo en equipo y una evaluación individual, así como el G1, referentes a los contenidos de la mitad del semestre hasta el fin, correspondiendo a integración de funciones reales de una variable, técnicas de integración y aplicaciones de integrales en ejercicios en forma de problemas.
En la primera parte del semestre, hay como contenidos asuntos referentes a derivación de funciones de una variable – algébricas, racionales, exponenciales, logarítmicas, trigonométricas y sus inversas –, temas presentados a los estudiantes de cálculo de una derivada originada por límites, bien como la obtención de la ecuación de la recta tangente. También se estudiaron las técnicas de derivación – suma, diferencia, producto, división, regla de la cadena –; derivación implícita y de orden mayores que uno; regla de L’Hôpital; análisis de funciones – puntos críticos y de inflexión, concavidad, extremos relativos y absolutos.
En la segunda parte del período lectivo, los contenidos estudiados se refieren a la integración de funciones de una variable, lo mismo que en la primera mitad de la asignatura. De este modo, se estudiaron las técnicas integrales definidas (que tienen como resultado un número real) e indefinidas – substitución y por partes; o bien como el Teorema Fundamental del Cálculo.
Como técnica de análisis de datos se hizo uso de la estadística descriptiva por medio del cálculo de promedio y porcentajes, vía representación de cuadros para exposición de los resultados. Se enfatizó que para el cálculo de porcentaje se utilizaría como total el 100%, como se fundamenta con antelación.
A continuación, se presenta el análisis de datos con la discusión de los resultados, las consideraciones finales y las referencias utilizadas en este estudio.
Rendimiento académico en las ingenierías: análisis emergentes
Analizar el rendimiento de los estudiantes de las carreras de ingeniería a lo largo de un semestre en la asignatura de CDI I puede traer percepciones acerca del aprendizaje en un determinado contexto educativo, las recomendaciones para hacer futuras intervenciones docentes se realizaran a partir de los resultados presentados en este apartado realizando el respectivo análisis y la respectiva discusión.
Por lo tanto, se inicia con el análisis del cuadro 1 en que se muestra la situación de los académicos de la carrera de Ingeniería Ambiental.
|
|
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería Ambiental. |
Como se puede observar en el cuadro 1, en la asignatura de Cálculo I cursaron tres alumnos de la especialidad Ambiental de estos tres, solamente uno fue aprobado, con promedio 6,0, o sea, A42 quedó con el mínimo para aprobar la materia. Los otros dos, no obtuvieron una calificación aprobatoria por lo que son considerados reprobados, teniendo el alumno A30 promedio 4,3 y A21 con 4,5.
Notase, que A42 tenía en la época del análisis 18 años de edad, estaba en el 4º semestre del curso y no trabajaba. Ya A30 poseía 25 años, estaba en el 6º semestre y trabajaba y A21 tenía 26 años, cursaba el 2º período y no ejercía actividad remunerada. En cuanto a los exámenes percibe que la mayor dificultad de los estudiantes que reprobaran fue en el G2, que abordaba los contenidos de integrales y que en la prueba de substitución su calificación fue más baja que antes.
Eso parece mostrar que ellos no estudiaron para el examen, que mantuvieron las mismas dificultades, según Pace (1984), Harper y Quaye (2009) y Perreaudeau (2009), los alumnos no invirtieron tiempo para el estudio de la asignatura, es decir, que los estudiantes no se prepararon, sabiendo que necesitaban retomar la materia o no encontrarían una estrategia para lograr mejorar el aprendizaje.
A continuación, se presenta el cuadro 2, con datos correspondientes a la carrera de Ingeniería Civil.
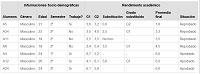 |
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería Civil. |
En el cuadro 2, se percibe que hubo siete alumnos en la especialidad Civil. De estos siete, tres aprobaron y cuatro reprobaron, o sea, hubo más estudiantes con bajo rendimiento académico que el opuesto, analizando el cuadro 2 podemos notar que aún los estudiantes que obtuvieran aprobación en la asignatura, quedaran con el promedio mínimo de 6.0, solo uno hizo el examen de substitución de grado, tal vez por ello, los otros dos no tuvieron un rendimiento mayor.
En relación a la edad, según los datos presentados, existen alumnos cuyas edades fluctúan entre los 18 y 24 años. En cuanto al aspecto “trabajo”, todos los aprobados trabajaban en la época de la recopilación de datos y el 75% de los reprobados no ejercían actividades laborares, es decir, que se presupone que tenían más tiempo para dedicarse a los estudios de la materia en comparación con los trabajadores.
De acuerdo con Guzmán (2004), la situación de estudiantes trabajadores es muy común en diversos países, sea por cuestión familiar, económica y política, entre otras. Allá de eso, la autora también afirma que esta característica de una parte de académicos, puede influenciar directamente en su desempeño en las diferentes asignaturas, principalmente en las que necesitan de mayor inversión de tiempo para su aprendizaje.
Ya en cuanto a los exámenes, se observa que la mayor dificultad de los estudiantes que reprobaran fue en el G1, contrastándose con la carrera anterior. En este caso, se puede deducir que el alumno que tuvo éxito en la asignatura fue el que podría dedicar más tiempo al estudio y que tenía una base matemática elemental más fuerte en relación a los demás, pues según Pace (1984), un estudiante que tiene un mejor desempeño, se prepara antes, durante y después del aula.
Cavasotto (2010) menciona que la dificultad en derivadas puede ocurrir por falta de conocimiento matemático básico, cosa que los alumnos aprobados aparentan tener. Así, los otros alumnos más grandes no consiguieron lograr, posiblemente por no comprender los conceptos de derivación y sus técnicas, que necesitan conocimientos en funciones, trigonometría, ecuaciones polinominales, entre otras
A continuación, se presentan los resultados del cuadro 3 correspondiente a la carrera de Ingeniería de la Computación.
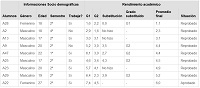 |
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería de la Computación. |
Analizando el cuadro número 3, se observa que en la asignatura de Cálculo I tenían nueve estudiantes, dos de sexo femenino y los otros siete de sexo masculino. De los hombres, no hubo ninguna aprobación; es decir, que todo el universo masculino de la carrera de Ingeniería de la Computación que estaba cursando la materia en el semestre analizado obtuvo calificaciones con promedio abajo de 6,0. Entre el universo femenino, hubo la mitad de aprobaciones y reprobaciones, o sea, una alumna aprobó y la otra no, es interesante resaltar que de esta carrera, siete personas ejercían actividad remunerada y dos no, siendo un alumno y una alumna.
Se puede observar que la edad promedio del grupo fue entre de 18 a 24 años y que el grupo tuvo bajo rendimiento en el G1 y G2. Sin embargo, en las integrales los estudiantes tuvieron bajo resultados en relación a los contenidos de derivación.
De esta manera se puede concluir que en esta carrera las dificultades en las matemáticas son evidentes y se vuelve importante pensar sobre el aprendizaje de estos alumnos (Cavasotto, 2010; Pereira, 2009), de manera que se pudiese hacer otra investigación para revisar cómo están estés estudiantes en el curso o como fue el rendimiento en las asignaturas de matemáticas cursadas hasta hoy.
En el cuadro 4 que se presentan los resultados del rendimiento de los Estudiantes de Ingeniería de Producción.
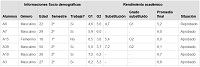 |
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería de Producción |
Analizando el cuadro 4, se puede observar que había seis estudiantes, cinco hombres, todos en el segundo semestre del curso y que ejercían actividad remunerada; y una mujer con dieciocho años de edad que en su primer periodo no trabajaba en la época de la recopilación de datos. Se puede observar que de los seis alumnos, solamente uno reprobó ya que realizó el examen de substitución de G1. Los demás tuvieran éxito en esta asignatura, algunos con dificultades en el G2 abordando los contenidos de integrales y de funciones de una variable.
En ese sentido, se aprecia que prácticamente los estudiantes de Producción tuvieron un bajo rendimiento en el G2 en relación al G1, así como las especialidades de Ambiental y Computación, por lo que podemos constatar hasta ahora que, en general, los alumnos tuvieron dificultades de aprendizaje en las integrales. Según Rezende (2003), las dificultades en integrales son de origen epistemológicas, de modo que el alumno tiene problemas para construir el concepto de integral a lo largo de su aprendizaje, debido al proceso de reversibilidad, que se vuele más complejo que la operación directa, que en este caso, sería las derivadas. Eso podría ser una de las razones para la dificultad de este grupo de Ingeniería Ambiental y de Computación.
Por ello, hay que analizar otros grupos para verificar si es un problema específico de este contexto o si es un problema generalizado, para ir pensando en intervenciones docentes para mejorar el aprendizaje del cuerpo discente.
El cuadro 5 presenta los datos de la carrera de Ingeniería Química.
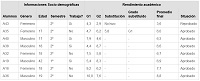 |
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería Química |
De acuerdo con el cuadro 5, la carrera de Ingeniería Química tiene ocho estudiantes, siendo cuatro alumnas y cuatro alumnos, todos con edades que fluctúan entre los 18 y 24 años de edad en el segundo periodo del curso, excepto el A19 que tenía 42 años y estaba en su primer semestre de la carrera, en cuanto al rendimiento de los estudiantes, se constata que ellos tuvieron un desempeño variable, es decir, que tres estudiantes (A19, A35 e A38) salieron mejor en el G2 y los otros cinco en el G1, por lo que se puede afirmar que este grupo tuvo un mejor aprendizaje en los contenidos de derivación y sus técnicas, comparadas con las ya analizadas, a no ser la de especialidad Civil. Sin embargo, se resalta que en el mismo rango del G1, los alumnos A19, A35 e A38 mejoraron en el G2 el promedio de la segunda mitad del semestre, eso significa que ellos, quedaran con rango abajo de 6,0 en las derivadas.
En relación al éxito o fracaso de la asignatura, podemos observar que hubo apenas una reprobación en esta carrera que demuestra que al parecer los estudiantes se comprometieron con su aprendizaje, o sea, se prepararon a lo largo del semestre en el Cálculo, obteniendo éxito en Cálculo Diferencial e Integral I.
Se presenta el cuadro 6, referente a la última carrera analizada en este artículo – Ingeniería de Telecomunicaciones.
|
|
Promedio de las evaluaciones G1, G2 y calificación final de los alumnos de Ingeniería de Telecomunicaciones |
En el cuadro 6, se observa que hay solamente dos alumnos en la especialidad de Telecomunicaciones, siendo ambos del segundo semestre del curso, A46 siendo del sexo femenino, con 32 años y trabajando y A26 del género masculino, con 18 años y no ejerciendo actividad laboral. Se destaca que los dos tuvieron promedio positivo, o sea, los estudiantes aprobaron en la asignatura y no necesitaron hacer examen de substitución.
Observando los datos, se verifica que la alumna tuvo un rendimiento mejor en las derivadas y el alumno en las integrales, o que no se puede generalizar un supuesto para este curso, pues no se sabe el histórico académico anterior de ellos y sus backgrounds en matemáticas, es decir, su conocimiento previo de la materia (Cavasotto, 2012). Finalmente, se presenta en la tabla 1 el número de aprobaciones y reprobaciones por carrera y género a lo largo del segundo semestre de 2013 en las especialidades de Ingeniería.
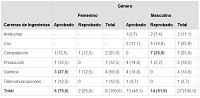 |
Situación final de los alumnos de ingeniería en la asignatura de Cálculo I en 2013/02 |
En relación a los géneros, se puede percibir que en el sexo femenino hubo 6 (75,0%) logros en la asignatura, teniendo a la carrera de Ingeniería Química como el curso con mayor porcentaje de alumnos aprobados, con 3 (37,5%) alumnas. En cuanto a la reprobación de las alumnas, se tuvieron dos casos, 1 (12,5%) en Ingeniería de la Computación y 1 (12,5%) en Química.
En el sexo masculino, nótese que el número de aprobados fue un poco menor que los reprobados, correspondiendo a 13 (48,1%) e 14 (51,9%), en esta orden. En cuanto al éxito, el mayor número ocurrió en las especialidades de Producción y Química, las dos con 4 (14,8%) éxitos. La reprobación de los alumnos, tuvo una concentración preponderante en la carrera de Ingeniería de la Computación, con 7 (25,9%) alumnos, seguido de la carrera de Ingeniería Civil, con 4 (14,8%).
Una de las conclusiones es que las mujeres siendo minoría en las carreras de Ingeniería (Vargas, 2010; Leta, 2003), tuvieron más éxito (porcentual) que los hombres en cuestión de las especialidades, se percibe que la carrera de Producción y Química fueron más exitosas que las demás y que Computación fue la que más necesita de atención en este grupo.
A continuación se presentan las consideraciones finales de este trabajo y sus respectivas referencias.
Consideraciones finales
El texto presenta reflexiones originadas en una investigación de un Estudio de Caso, cuyo objetivo fue analizar el rendimiento académico de los estudiantes en la asignatura de Cálculo Diferencial e Integral I (CDI I).
El rendimiento académico en Cálculo Diferencial e Integral I es el reflejo del que hacer del estudiante a lo largo del período lectivo, es decir, que su promedio, está influenciado por diversos factores, entre ellos su dedicación y compromiso para con el estudio de la asignatura, estudiando los contenidos enseñados y los anteriores que son necesarios para fortalecer su aprendizaje y avance del conocimiento matemático; el proceso de enseñanza desarrollado por el profesor; las aplicaciones de la materia para significar el aprendizaje, entre otros (Barbosa, 1994; Rezende, 2003)
Es importante mencionar que la formación en matemáticas del estudiante de Ingeniería no se da solamente en la Enseñanza Superior, pero si en toda su trayectoria escolar y académica, es decir que su contacto con esta área ocurre desde la Educación Básica y que seguramente las probables dificultades que tienen en alguna asignatura en la universidad la cual necesita de los conocimientos matemáticos producto de su formación – Cálculo, por ejemplo – el reflejo de un histórico muy anterior al semestre lectivo en cuestión (Rezende, 2003). Basado en Laros, Marciano y Andrade (2010) se puede tener una idea de que los alumnos que salen de la Educación Básica no tienen el conocimiento esperado en Matemáticas, pues de acuerdo con su investigación en que analizaran el desempeño discente en el Sistema de Evaluación de la Educación Básica de Brasil, los alumnos de la preparatoria no consolidan los niveles deseados para esta etapa y que hay factores que influyen en esto – nivel socioeconómico, apoyo familiar, formación docente, entre otros. Eso nos hace pensar que muchos de estos estudiantes son los que están en la universidad y una parte en las carreras de Ingeniería, además de las dificultades que se presentan en la universidad además forma parte de un conjunto previo ya existente desde los niveles educativos anteriores.
Desde esta perspectiva se puede también complementar que el desempeño académico de los estudiantes, también está relacionado con el abordaje metodológico desarrollado por el maestro desde en la Educación Básica esto significa que el alumno tiene responsabilidad con su formación, sin embargo el profesor está involucrado en este contexto, una vez que él debe mediar el proceso de enseñanza y aprendizaje de modo que se pueda proporcionar al discente una visión más clara del contenido por medio de distintas estrategias de enseñanza para que se pueda contemplar los estilos de aprendizaje de los estudiantes (Gauthier et al, 2006; Perreaudeau, 2009).
Conclusiones
El objetivo de la presente investigación fue analizar el rendimiento académico de los estudiantes de las carreras de ingeniería en la asignatura de Cálculo Diferencial e Integral I al largo del segundo semestre lectivo de 2013, obteniendo como conclusiones finales, de acuerdo con los datos expuestos con anterioridad:
- Hay diferencias en el aprendizajes de los alumnos de las carreras de Ingeniería Química, Telecomunicaciones y Producción obteniendo el mejor desempeño en la asignatura de Cálculo I, y las demás con mayor fracaso de los alumnos de las demás especialidades;
- Se puede pensar en ofertar la asignatura por curso y no de modo mixto, pues con rendimientos muy distintos y necesidades diferentes en cada carrera, el profesor podrá preparar los contenidos de forma más direccionada para los estudiantes y no de modo general, que muchas veces, parece a ellos sin interlocución con su formación académica (Barufi, 1999; Ferrão, 2012);
- No se puede establecer una predicción de rendimiento académico entre los estudiantes que trabajan y no ejercen actividades remuneradas, porque los datos muestran una variabilidad entre los resultados de aprobación y reprobación. Lo que se puede concluir en este caso, es que el suceso relacionase con la intensidad en el tiempo de estudio de los estudiantes y no con su condición profesional;
- Continua la baja elección de las carreras de Ingeniería entre el cuerpo discente femenino (Leta, 2008; Vargas, 2010), no habiendo ninguna en las áreas de Ambiental y Civil, pero las mayoría de las alumnas que cursaran las demás especialidades obtuvieron un rendimiento en el Cálculo I 60% del total fueron aprobadas y 40% reprobadas en la asignatura de Química y Producción;
- En general, la mayor dificultad de los estudiantes de este equipo fue en los conceptos de integración de funciones de una variable, que también es conocida como anti derivada, o sea, es la inversa de la derivada, con excepción de la Ingeniería Civil;
Esta investigación apunta en la necesidad de intervención teórica y práctica con mayores estudios en el área de la enseñanza y aprendizaje de Cálculo Diferencial e Integral I, pues se vuelve importante buscar soluciones para disminuir el fracaso en la asignatura, no solamente en el contexto analizado, sino en todo el escenario internacional (Vitelli, 2012; Mosca, León y Rubio, 2012; Gonçalves, 2012).
Surgieron también, algunas preguntas que podrán ser desarrolladas en futuros estudios: a) ¿Qué intervenciones docentes serían efectivas para con los alumnos de Cálculo Diferencial e Integral I objetivando mejorar su aprendizaje?; b) ¿Cuáles son los impactos a lo largo de la formación académica y profesional de los estudiantes con bajos rangos en las asignaturas de Cálculo Diferencial e Integral?; c)¿Cuáles son las diferencias en el aprendizaje de Cálculo I entre hombres y mujeres y sus influencias en su acción profesional?.
Se espera que las reflexiones presentadas puedan contribuir para el avance de las investigaciones en el área de la Educación Matemáticas y más específicamente para la asignatura de CDI I en lo que se refiere a los procesos de enseñanza y aprendizaje en este componente curricular.