LAS TRANSFORMADAS DE FOURIER, HARTLEY, WALSH, HAAR, Y MAXIMA ENTROPIA : COMPARACION, .JSO EIMPLEMENTACION EN COMUNICACIONES Y ELECTRONICA
E. Gómez Ramlrez
Universidad La Salle Laboratorio del Centro de Investigación
RESUMEN
Durante mucho tiempo una de las técnicás más utilizadas para el análisis de espectro, ha sido la transformada de Fourier desde que su autor Jean
Baptista Joseph Fourier la definiera . A partir de ese momento, las áreas en las cuales era útil, fue aumentando, al mismo tiempo que la cantidad de
datos y operaciones que se requerian para su obtención. Debido a esto. hubo un gran desarrollo en nuevos algoritmos que hicieran este análisis.
Actualmente, existen otros algoritmos para el análisis de espectro de una función, como son: Transformada de Hartley, Walsh. Haar y Máxima Entropla.
Cada uno de estos algontmos tiene diferentes ventajas y aplicaciones dependiendo de la naturaleza de los datos.
En este trabajo se presenta la implementación en software de las transformadas antes mencionadas y su comparación en el análisis de espectro de
diferentes funciones.
INTRODUCCION
El análisis de espectro es una herramienta importante en una gran cantidad de áreas. por lo que se han desarrollado diferentes algoritmos para su
aplicación. Uno de los primeros algoritmos fue el de la Transformada de Fourier, pero debido a que en su tiempo no se tenía un desarrollo óptimo de
cálculo para la gran cantidad de datos y número de operaciones que se necesitaban. se buscaron nuevos algoritmos para su implementación; uno de ellos
fue elaborado en 1965, por James W. Cooley y John W. Tukey. El trabajo de ambos dió lugar a un programa conocido por Transformada Rápida de Fourier
(FFD. Este algoritmo realiza la transformación en menor tiempo que la Transformada Discreta de Fourier. reduciendo el número de multiplícaciones
necesarias.
Otro de los algoritmos utilizados para la transformació n del dominio del tiempo al dominio de la frecuencia de una función. es el de la Transformada
de Hartley, cuyo algoritmo no utiliza números complejos y del cual se puede extraer la misma información de amplitud y de fase que la obtenida por la
FFT.
La Transformada Rápida de Hartley (FHD (Bracewell,1986) utiliza menos recursos computacionales, debido a que utiliza el mismo algoritmo para la
transformada . como para la antitransformada y los resultados se obtienen en menos tiempo que la FFT.
TRANSFORMADA DE FOURIER
La Transformada de Fourier F(t) se define como:
F(f)
= L:V(t)e-ri nndt (1)
donde: t es tiempo
f es frecuencia
V(t) es la función en tiempo
e
-
Q.itft
= cos(2 nft)- isen(2nft)
Considerando las propiedades de simetría la Transformada de Fourier se puede separar en 2 funciones : una función par E(t) (f(t)=f(-t)) y una función
impar O(t) (f(t)=-f(-t)) expresada como:
E(f}
= r..V(t)cos(2nft}dt (1.1)
O
(f)
= J:V(t}sen(2nft)dt (1.2)
De esta manera se puede definir la f (f) como:
F(f)=E(f)-iO(f)
F(f)
= r..V(tX cos(2 nft) - isen(2 nft)]dt (2)
De donde .el espectro se puede definir como:
P
(f)
= IF(f = E(fJ + O(tf (3)
TRANSFORMADA DE HARTLEY
La transformada de Hartley H(t) se define como:
H(f)
= r_ V(t)cas{2 rtft} (1')
donde:cas (2rrft) = cos(2rcft) + sen(2nft)

Expresando H(f) en función de E(f) y O(f) (funciones par y non) se tiene que:
H(f) = E(f) + O(f) ( 2')
H(f):
A su vez , E(f) y O(f) pueden ser expresados en función de la Transformada de Hartley
E(f) = H(f)+ H(- f)
2
O(f)= H(f)- H(-f)
2
(2.1 ')
(2.2')
Para obtener el espectro, en función de H(f).
 P(f)
= E(tf + O(f)2
P(f)
= E(tf + O(f)2
 P(f)
=
J(H(f)+ H(-f)r +(H(f) - H(-f))'
P(f)
=
J(H(f)+ H(-f)r +(H(f) - H(-f))'
2
2
P(f)
= H(tf +
H(-fj
2
(3')
De las ecuaciones 3 y 3' se puede observar que se obtienen los mismos resultados para obtener el espectro por las dos transformadas (se puede hacer un
análisis similar para la fase).
En las figuras 1,2,3 se puede observar una función muestreada y su espectro obtenido por FFT y FHT.
TRANSf!ORMADA DE WALSH
Una función de Walsh consiste en un conjunto ordenado de sei'lales rectangulares cuyas amplitudes sólo tienen dos valores. +1 y -1.
Se definen sobre un intervalo de tiempo, T, conocido como base de tiempo, que es necesario conocer para asignarle un valor a cada función . Al igual
que las funciones seno y coseno, las funciones de Walsh se definen con dos argumentos: un tiempo t (comúnmente normalizado con la base de tiempo, tJT) y un orden, n, relativo a la "frecuencia" (número de cruces por cero). La función de Walsh se denota:
WALSH{n ,t).
Una serie de funciones de Walsh se representa sobre un intervalo abierto (O,1) como:
X(t)
=
a
0
+ a,
WALSH(1,
t)+
a2 WALSH(2, t)....
donde cada coeficiente ªk se puede expresar como:
ak
= Jf(t)WALSH{k, t)dt
(4.2)
con lo que se define el siguiente par de transformadas:
f(t)
=
2.F{k)WALSH{k,
t)
K>-.0
(4.3)
F{k)
= j f(t)WALSH(k, t)dt (4.4)
La Transformada Discreta de Walsh se define como:
1 N-1
X,, =
-¿_ x,WALSH(n,í) N 'i=O
(4.5)
y su antitransformada como:
N-1
x
i
=
¿
x
,,
WALSH(n,i)
n=O
(4.6)
donde: n es el número de función de Walsh.
La Transformada rápida de Walsh es más rápida que las Transformadas de Fourier y Hartley, debido a que las multiplicaciones realizadas al momento de
obtener la transformación , son con valores de 1 y -1 y no funciones trigonométricas.
TRANSFORMADA DE HAAR
Una función de Haar es un conjunto de señales rectangulares con amplitudes que asumen tres valores: O, +A y -A. El valor de ±A está en función de _2. A
diferencia de las funciones de Walsh. estas amplitudes también dependen de su lugar en el intervalo de tiempo T.
La función se denota:
HAR(n ,t)
donde :
n indica el número de función de Haar.
Al tomar una función continua f(t) periódica en el intervalo O_t_1, con período 1 (este valor está normalizado para la ventana utilizada), f(t) se
puede expresar como una serie de funciones de Haar tal que:
f(t)
=
L,C,,HAR{n, t)
n-so
(5.1)
e,, = Jt(t)HAR(n, t}dt (5.2)
de estas últimas ecuaciones se establece la Transformada discreta de Haar como:
1 N-1
X
,,
=
-I,xtfAR(n, i/ N)
N
.1=0
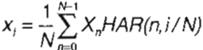
i,n = O, 1, . . . N-1
(5.3)
(5.4)
Esta transformada es similar a WT pero el tiempo de cálculo es menor, debido a que se presentan modificaciones en el desarrollo del algoritmo.
y el número de operaciones que se efectúan es menor, por lo que es más rápida con respecto a FWT y FFT. En las figuras 4,5,6 se presenta una función y
su espectro por FWT y FHAT.
ESPECTRO POR EL METODO DE MAJCIMA ENTROP A (MEM)
El espectro de Potencia puede ser expresado como (Press,1986):
 P
(
f
)
= .,....-- ª-º=--
P
(
f
)
= .,....-- ª-º=--
m
1+L,akr
k..1
(6.1)
donde: m = es el número de polos z = ei21tf
ªO···ªk son valores constantes.
A su vez, del teorema de Wiene r-Khinchim,que puede ser enunciado como sigue :
"La Transformada de Fourier de la autocorrelación de una función es igual al espectro de potencia".
el espectro de potencia, también puede ser expresado como:
P(f} =
_
m
8
;
m
= L<P¡z'
(6.2)
1+ L,aki' J=-m
k=.1
donde:
0j es la autocorrelación de la función muestreada.
Para obtener Jos coeficientes ao. a 1,....ak se tiene que cumplen con la siguiente relación:




|
<Po
|
$1
|
<ll2
|
$m
|
|
$1
<P2
|
<l>o
<P1
|
<P1
<Po
|
<Pm-1
<l>m-2
|
|
<l>m
|
<Pm-1
|
<Pm-2
|
<Po
|
|
|
1
ªº
ª1
ª2 o (6.3)
am
o
de donde por el método de Burg y Andersen (Press, 1986) pueden ser obtenidos los valores de estos coeficientes.
Los resultados obtenidos con este método muestran que con un valor de polos específico (diferente para cada función) es especialmente útil para
funciones que tienen cierto nivel de ruido, por ejemplo , los datos obtenidos en un experimento o alguna señal como puede ser la de voz. A diferencia
de las otras transformadas , por no tratarse de una transformada rápida.la cantidad de datos no tiene que ser potencia de dos. pero el tiempo de
cálculo es mayor y se incrementa con la cantidad de datos y polos seleccionados.

CONCLUSIONES
La cantidad de áreas y aplicaciones del Análisis de Espectro ha ido creciendo, por lo que es necesario el conocimiento de nuevos algoritmos (Loza,1990)
(Plascencia,1990) aplicables a diferentes casos y situaciones (nivel de ruido, mayor rapidez y capacidad de cálculo).
El utilizar este tipo de herramientas como alternativa a las que existen en el mercado de análisis de señales (DSP) (que por lo general utiliza el
algoritmo de FFT) permite manipular de forma directa y más rápida parámetros del espectro que se requieran en el desarrollo de investigación en el área
de análisis de señales.
BIBLIOGRAFIA
Beuachamp, K. G. (1975)." Walsh Function and their applications". University of Lancaster.
Academic Press, Great Britain.
Bracewell,R. (1989) "La Transformación de Fourier". Scientific American. p.56-64,Agosto. Bracewell,R. (1965) "The Fourier Transform and its
aplications" McGraw-Hill,USA. Bracewell,R. (1986) "The Hartley Transform", Oxford University Press,New York.
Brigham, E. (1974) "The Fast Fourier Transform". Prentice Hall, USA.
Del Vivar Plascencia, Rayón Villela, P.. Figueroa Nazuno, J .. (1990). Implementación de un programa de estimación de máxima entropía bidimensional, XXXIII Congreso Nacional de Física, 22 al 26 de ocJubre. Ensenada, Baja California, México.
Loza Garay,E., Carrera Abarca, M., Franco Gutierrez, L.,& Figueroa Nazuno, J. (1990) • Implementación de la Transformada de Fourier para grandes
volúmenes de datos. XXXIII Congreso Nacional de Físíca. 22 al 26 de octubre, Ensenada, Baja California, México
Montaño,J.C.,Florida,M.C.,Castilla. M.. López. A.. Gutiérrez. J. (1986). Realización de la FFT en PC. Mundo Electrónico, 73-80. Diciembre.
O'Neill,M. (1988) "Faster than Fast Fourier", BYTE,p. 293-300,Abril.
Press, William H., Brian. Flannery P.. Teukolsky, Saul A.. Vetterling, William T. (1986) "Numerical Recipes", Cambridge University Press, USA.
Thrane,N. (1979) "The Discrete Fourier Transform and FFT Analysers", BrÜel & KJ.tER. Technical Review, no.1.

J. \.
 ,,,_ Un' La ale ----.---------r-- - ----------,
,,,_ Un' La ale ----.---------r-- - ----------,
 1
1
1
F (t) = SIH2.T PUNTOS = &4 Y MAX = 1 MIH = -1
FIGUR
ll
SEÑAL SENOIDAL

 TRANSF DE f(t) = SIH2 .T H = 64 Y MAX = .5 MIN = -6.922913E-09
TRANSF DE f(t) = SIH2 .T H = 64 Y MAX = .5 MIN = -6.922913E-09
FIGURA
2
T
RANSFORMADA DE FOURIER

 VALOR MAYOR = .5
VALOR MAYOR = .5
VALOR MENOR = 1.50B228E-09
FIGURA 3 TRANSFORMADA DE HARTLEY








1 1 tfíl
n n n
n r1 -n 1 \
n 1 11 11 11

t+.._.. H-'-t H· 4-+ t-H-H-+- .......J,. -+it- ·!-+ H-'-+ +++-+++ ++t+-H+4i +++4- : ---1

 F(t) = U31.T PUNTOS = ó4 Y MAX = 1 "IN = -1
F(t) = U31.T PUNTOS = ó4 Y MAX = 1 "IN = -1
FIGURA . CION 31 DE WALSH
 ,---·--·-·--·-·
,---·--·-·--·-·
·
-·
1
1
!

 ··-· -· -._._
··-· -· -._._
---+-+-+-·...:.;-+---' ----,-----¡
TRAHSF DE FCt) = W31.U H = ó4 Y MAX = 1 MIM = 0


 FIGURA 5 TRANSFOR ADA DE WALSH
FIGURA 5 TRANSFOR ADA DE WALSH


 1
1
1
1
1 1

 Ll ....... i '_' _¡ :_: _: ·_'_' '_' '_¡ J 1_1 : '_' ,_. _· :_, _._' !._:_· '_' ' i . ' 1 . 1 . i 1 1 ¡ 1 1 ¡
Ll ....... i '_' _¡ :_: _: ·_'_' '_' '_¡ J 1_1 : '_' ,_. _· :_, _._' !._:_· '_' ' i . ' 1 . 1 . i 1 1 ¡ 1 1 ¡




TRAHSF DE F(t)= W31.HA H = 64 Y MAX = .0625 "IH = 0
FIGURA 6 TRANSFORMADA DE AAR
![]()
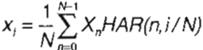
 ,,,_ Un' La ale ----.---------r-- - ----------,
,,,_ Un' La ale ----.---------r-- - ----------,




 F(t) = U31.T PUNTOS = ó4 Y MAX = 1 "IN = -1
F(t) = U31.T PUNTOS = ó4 Y MAX = 1 "IN = -1
 ,---·--·-·--·-·
,---·--·-·--·-·
