ANÁLISIS ELECTRÓNICO Y COMPUTACIONAL DEL FENÓMENO DE SINCRONIZACIÓN DE SISTEMAS CAÓTICOS .

Hugo Gustavo González Hernández y José Carios Ángeles Femández Laboratorio del Centro de Investigación .

UNIVERSIDAD LA SALLE

RESUMEN

En este trabajo se presenta y analiza, tanto electrónica como computacionalmente. una forma de sincronizar un subsistema de un sistema caótico con una señal de un sistema caótico similar de tal manera que las señales correspondientes de los dos sistemas sean idénticas. Este análisis puede ser trivial para el caso de sistemas lineales pero no para el de sistemas no lineales y menos aún para sistemas caóticos. Para este trabajo se construyó un generador de caos en forma sencilla, usando un oscilador inestable de segundo orden y un elemento de histéresis para realizar el sistema sincronizador, y se utilizó un subsistema de éste como sistema a sincronizar. Se

presentan los resultados del análísis electrónico y de la simulación en computadora .

I NTRODUCCIÓN

El fenómeno de sincronización ha sido ampliamente usado en electrónica (televisores, radares, osciloscopios, relojes electrónicos). En general una pequeña señal periódica de sincronización con un período dado es usada para manejar un sistema que puede producir una señal más grande con período de un valor cercano al de la pequeña señal de tal forma que la señal controlada se ajuste al período de la pequeña señal ( o a algún múltiplo o submúltiplo de ésta).

Existen muchos mecanismos posibles para ésto, pero el más común en Teoría de Circuitos Eléctricos es el mecanismo de umbral,en el cual, el sistema controlado produce una salida que depende de que se alcance o no un cierto nivel llamado de umbral. En este caso la sel'lal de sincronización actúa causando que el nivel de umbral se alcance en un tiempo controlado.

Una sincronización exitosa depende de las relaciones apropiadas entre los niveles de la señal y de otros parámetros y del sistema a sincronizar. Cuando los parámetros están fuera de cierto rango, el sistema no está sincronizado y la salida no es periódica.

Para una amplia clase de sistemas que podemos analizar en detalle, la salida muestra características que son normalmente descritas como caos. Es decir que las soluciones son no­ periódicas, inestables bajo cierto rango, la señal exhibe un amplio espectro, caso continuo, y el sistema es hipersensible a cambios pequel'tos en las condiciones iniciales; ésto es que dos estados iniciales, muy cercanos uno del otro, presentan trayectorias de solución que divergen a largo plazo hasta llegar a no tener correlación alguna. En este trabajo, se presenta y analiza, tanto electrónica como computacionalmente un sistema caótico sincronizado por una señal de otro. Aunque estos sistemas son independientes entre sí y sus comportamientos no se correlacionan, es posible, bajo ciertas condiciones, sincronizar un subsistema de un sistema caótico con otro sistema caótico independiente, enviando una señal del sistema caótico al subsistema. La sincronización se lleva a cabo utilizando un generador de caos con un oscilador inestable de segundo orden y un elemento de histéresis.

DESCRIPCIÓN DEL PROBLEMA

Caos se ha descrito como una situación en la que un sistema pierde sincronización consigo mismo [1]. resultando en un complejo movimiento aperiódico. Si dos sistemas caóticos independientes tienen las mismas condiciones iniciales, cualquier pequeña diferencia en estas condiciones crecerá hasta que las soluciones sean totalmente diferentes. Sin embargo es posible sincronizar dos sistemas no lineales, a pesar de su comportamiento caótico si son sincronizadas con una señal apropiada. En este trabajo se muestra una forma de sincronizar un subsistema de un sistema caótico, con una señal de éste último, de tal manera que las señales correspondientes de los dos sistemas sean idénticas. Se construyó un generador de caos sencillo basado en un circuito desarrollado por Newcomb y 'sathian (2).

DESCRIPCIÓN DEL CIRCUITO

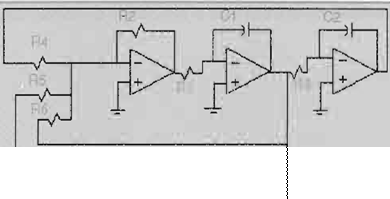El circuito electrónico se muestra en la siguiente figura:

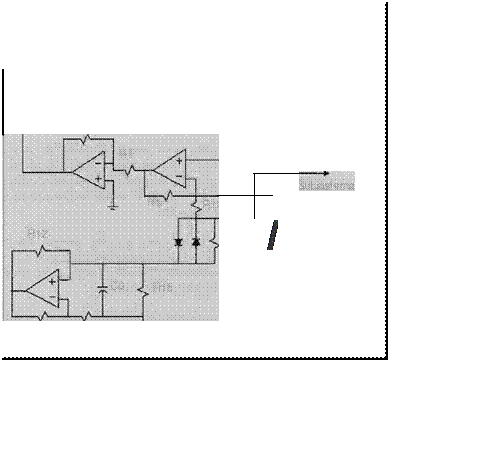
FIG. 1

Este circuito contiene un oscilador inestable de segundo orden que oscila a menos de 1KHz. El oscilador se conecta a un elemento de histéresis. La salida del elemento de histéresis provee la polarización que mueve el origen de un valor positivo a negativo para tener oscilaciones inestables. La amplitud de estas oscilaciones crecerá hasta que el voltaje X1 alcance la región de cambio del elemento de histéresis. Esto cambia el signo de la salida del elemento de histéresis moviendo el centro de la oscilación a un nuevo punto y manteniendo acotado el voltaje X1. Una vez que este punto central ha sido movido, el valor del voltaje X1 empieza a aumentar repitiendo el proceso. La histéresis añade el tercer grado de libertad.

El circuito se puede modelar mediante el siguiente sistema de ecuaciones diferenciales no lineales:

donde:

X 1 = X2 + ')'X1 +CX3

X2 = <.oX1 -S2X2

x3 = (1-x3 )(Sx1 - O + x3 ) -ó3x3

'Y = R2/R6 , C = R2/R5 , w = R1C1/R2C3

o2 y 83 son parámetros de amortiguamiento que modelan las pérdidas en el sistema.

Las ecuaciones para X1 y X2 modelan el oscilador inestable de segundo orden de la parte superior del circuito mostrado en la figura anterior. La ecuación para X3 está basada en una función usada por Rossler para modelar histéresis [3]. El voltaje X3 presenta histéresis dependiendo del voltaje X1. La constante es un valor pequeño lo cual ocasiona que la histéresis alcance rápidamente el valor de saturación mientras el voltaje X1 llega al punto de disparo. Las variables S y D se obtienen a partir de los voltajes de disparo superior e inferior (Vs y Vi).

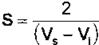D = SV¡ + 1

Para el régimen caótico se tiene 0.2, c=2.2, 02=0.001, o3=0.001, w=1O, S=1.667 y D=O.O.

SINCRONIZACIÓN

En el circuito a sincronizar se usa una resistencia variable para R(r). Esto nos pennite hacer un circuito-respuesta idéntico o no a la parte correspondiente del circuito sincronizador. La figura 2 muestra

un oscilograma de X2'(X2) donde X2' es el voltaje X2 del circuito a sincronizar para una R(r) = 20K.Q =

R. En este caso los dos circuitos están sincronizados ya que fonnan una recta a 45º y las señales X2' y

X2 son iguales.

En la figura 3 se muestra el oscilograma de X2'(X2) para una R(r)=22K.Q. Los circuitos no están sincronizados y las dos señales son diferentes.

./

o o

FIG.2 FIG.3

1 ,...\,

Para un aumento en R(r) la diferencia entre las seflales X2' y X2 aumenta y por lo tanto los sístemas no están sincronizados.

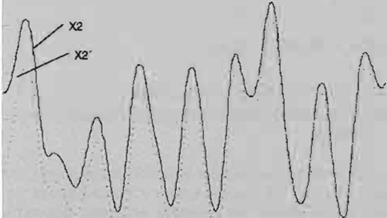
FIG. 4

Cuando los dos sistemas están sincronizados, las señales correspondientes en los dos sistemas son idénticas, si los dos sistemas tienen diferentes condiciones iniciales. la trayectoria del subsistema sincronizado converge a la trayectoria del sistema sincronizado< exponencialmente en tiempo. En la figura 4 se muestran las dos señales X2' y X2 en tiempo con diferentes condiciones iniciales. Esta simulación se realizó en una computadora personal utilizando un simulador de sistemas no lineales desarrollado en nuestro grupo [4].

CONCLUSIONES

En nuestro grupo hemos desarrollado trabajos en los que se realizan estudios paramétricos del fenómeno caótico [5-8]. Este tipo de realizaciones nos permiten visualizar de una manera más sencilla el comportamiento de estos sistemas tanto en el osciloscopio como en la pantalla de la computadora, así como manipular directamente los parámetros del sistema para poder analizar experimentalmente las condiciones bajo las cuales estos sístemas acoplados se sincronizan.

REFERENCIAS

[1] Oesoer, C. A. Notes for a second course on linear systems . New York, N. Y . van Nostrand Reinhold, 1970.

[2] Newcomb, R.W. & Sathian S. "An RC op amp Chaos Generator" . IEEE Transaction s on Circuits and Systems. vol. CAS-30, 1983.

[3] Rssler, O. E. "The chaotic hierarchy". Z. Naturforsch, vol. 38a, 1983.

[4] Angeles-Femández , J. C., González-Hemández. H., (1993). "SlMCAOS: A Non Linear Dynamics Slmulator". First lntemational Conference on Dynamic Systems and Applications, Atlanta GA U.S.A May, 1993.

[5] González-Hemández, H., Gómez-Ramírez, E., lbarra-Ramfrez, E. "Simulador elctrónico de Sistemas caóticos". León, Gto. XXXII Congreso Nacional de Física, León, Gto., del 23 al 27 de octubre de 1989.

[6] González-Hemández, H. "Análisis por técnicas computacionales y electrónicas del comportamiento caótico". México, UNAM Seventh lntemational Conference, Computers in lnstitutions of Education and of Research. October 23-25 . 1991.

[7] González-Hemández. H., Gómez-Ramírez, E. & Figueroa-Nazuno , J. "Análisis paramétríco del comportamiento caótico. implementación electrónica y computacional". Aguascalientes, Ags. 11 Congreso de la Asociación Nacional de Instituciones en Educación e Informática, 23 al 25 de octubre de 1991.

(8] González-Hemández, H., (1992). "El desarrollo y estudio de sistemas caóticos". Cholula Pue. Tercer Congreso Internacional de Electrónica y Comunicaciones CONIELECOM '91. UDLA, del 17 al 20 de febrero de 1992.