PREDICCION DE SERIES CAOTICAS UTILIZANDO REDES NEURONALES Y SU CORRELACIÓN CON EL EXPONENTE DE YAPUNOV

Eduardo Gómez Ramírez,Yesika Baeza Morales & Yudith Gornez Rubio LABORATORIO DEL CENTRO DE INVESTIGACIÓN

UNIVERSIDAD LA SALLE

RESUMEN

Existen hasta el momento diferentes aproximaciones para predicción de series de tiempo, por ejemplo algunas de ellas son: técnicas estadísticas, técnicas por filtro de Kalman, y en los últimos años se han reportado resultados de predicción con redes neuronales. Pero el problema sigue siendo saber si la serie es predecible "independientemente" de la técnica que se esté utilizando. En este trabajo se presenta la relación que existe entre el exponente de Lyapunov y el error de predicción para series caóticas por medio de redes neuronales, como instrumento de decisión en el área de predicción. Se presentan predicciones para mapeos discretos a partir de valores anteriores.

INTRODUCCIÓN

Se ha encontrado comportamiento caótico en una gran cantidad de disciplinas, por ejemplo: astronomía, biología, biofísica. química, ingeniería, geología, matemáticas, medicina, meteorología, ciencias sociales, etc. Esto ha permitido que se distinga entre sistemas que se pueden denominar ruidosos y sistemas que tienen un comportamiento en "Estado Estable" (1)(2)(3). Esta división es importante porque la aproximación define las herramientas o formalismos que se requieren para su análisis.

En el área de predicción de series de tiempo existen una gran cantidad de herramientas: modelos ARMAX (4), filtro de Kalman (5), y en los úl·timos años se han reportado resultados favorables utilizando redes neuronales (6)(7). Pero en ciertos casos los errores en la predicción dependen de la naturaleza de los datos. Por eso es que ecuaciones que tienen comportamiento caótico son utilizados como estándar ("Benchmark") de prueba para algoritmos de aprendizaje (8). Una de ellas es la seri e de Makey-Glass (9), pero existen una gran cantidad de mapeos discretos que también tiene este comportamiento (10)(11)(12).

Uno de los indicadores que se tienen para saber si una serie de datos es caótica es el exponente de Lyapunov. Si el exponente es positivo la serie es caótica y si el exponente es negativo la señal es periódica o converge asintóticamente a un valor.

En este trabajo se presenta la relación que existe entre el exponente de Lyapunov y el error de predicción de una red neuronal para mapeos discretos.

DESCRIPCIÓN

Mapeos Discretos, Mapa de Bifurcaciones y Exponente de Lyapunov.

Se escogió un mapeo discreto de la forma

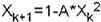Ec. 1

donde: k= 1, 2, 3 .....

La serie de tiempo generada depende de la condición inicial Xo y del valor de A En las figuras 1 y 2 se pueden obseNar el comportamiento de Xk, cuando A=0.4 y A=1.85

MAPE O DISCRETO A=0. 4 Xo=0.5

Xk 0.9

0,8

0.7

0.6

0 5

04

0.3

0.2

0.1

o .........¡-. + - K

·1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 1 22 23 24 25 26 27 28 29 30

FIGURA 1

MAPEO DISCRETO A=1.85 Xo=0.5

K

- l -

FIGURA 2

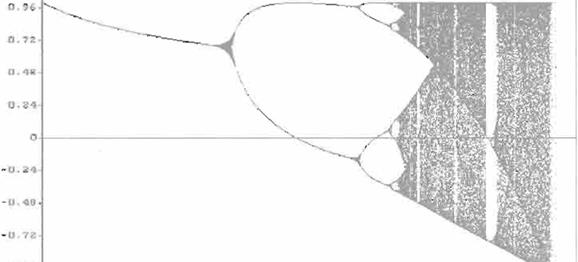
Si se eliminaran los transitorios y se graficaran los puntos contra el parámetro A. se obtendría una gráfica que se denomína mapa de bifurcaciones (fig. 3). En este mapa se puede obseNar para que valores de A el sistema presenta comportamiento caótico. Este mapa fue obtenido por medio del programa SIMCAOS (13)(14).

- (1 9 .

r/,- 11'1 .- -"..'... ---;:' Cll O o N ' • ..;

l .Z-· -,--, --.· -----· .. .....,.--.

o

ó o

CI ) ., ..

...

"'

..,

FIGURA 3

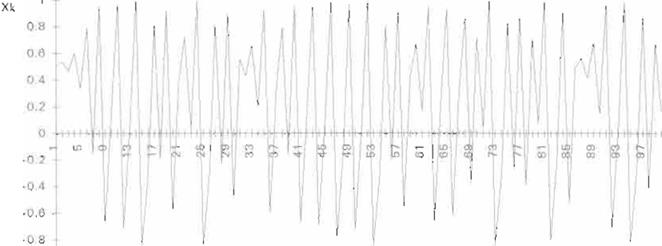
Otra forma de analizar el comportamiento caótico de la Ec. 1 es obteniendo el exponente de Lyapunov para distintos valores de A (fig. 4}. (15).

EXPONENTE DE LYAPUNOV

o . ....... ... ..

0.5

- ....-

-v.', o

- ,

• ·1 "

' ) •

::> f, •

.3 ..

., e

• J

.. 1 .... W" l. 8 • 2 A

D ••••••

•

D •

FIGURA 4

Como se puede obseNar en la figs. 3 y 4, el exponente de Lyapunov negativo corresponde a estados periódicos o que convergen asintóticamente a algún valor. y el exponente de Lyapunov positivo corresponde a régimen caótico.

REDES NEURONALES

Las redes neuronales han demostrado gran capacidad de predicción en distintas áreas, principalmente donde no se conoce el modelo matemático del sistema. Para cada una de estas aplicaciones existen diferentes formas tanto para la arquitectura de la red como para las etapas de procesamiento de los datos de entrada, dependiendo de la aplicación y de la naturaleza de los datos.

Para nuestro caso se va utilizar una red neuronal del tipo multicapa con función de activación sigmoide y como regla de aprendizaje la regla delta generalizada (16). Para los archivos de entrenamiento se van a utilizar los valores de -Z· -1, . como entradas y ..1

como salida para diferentes valores de A, generados de la Ec. 1. Los archivos de entrenamiento

no se procesaron para no afectar la dinámica delsistema.

DESARROLLO DEL EXPERIMENTO.

Primero se generaron series con k=1... 200 para una A determinada. Los primeros 50 datos no se utilizaron para eliminar los transitorios. Con los siguientes 100 datos se generaron los archivos de entrenamiento y los últimos 50 datos se utilizaron como entrada para probar la etapa de predicción de la red neuronal.

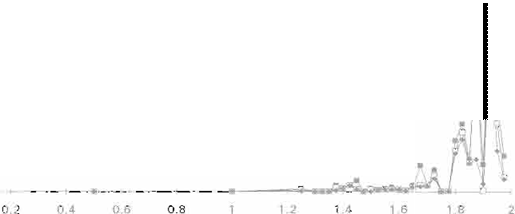
En la Fig. S se muestran los errores de predicción para distintos valores de A. Considerando el error de predicción como la diferencia entre la salida que da la red neuronal y la salida real de la serie.

ERROR DE LA REO NEURONAL

7 <:J OE-04

6.0CJf .()4

1o1:

ffi

ó.OOt·Oll 4.00E-04 DOE-04

l OOE·fl4

1.0íJE·04

0.00[+00

o

¡ - -

A

50()0 -':!- - lQOOO • • 1500(1 \te1aciom

FIGURA 5

RESULTADOS Y CONCLUSIONES

Como se puede observar en las figuras 4 y 5 los errores de predicción más altos corresponden a series donde el exponente de Lyapunov es positivo y mayor a 0.4 . Es importante hacer notar que el valor numérico de los errores puede ser distinto dependiendo de la condición

inicial utilizada tanto para los pesos de la red como para la Ec. 1. pero en todos los casos cumple con la condición que se mencionó anteriormente.

La red neuronal puede predecir el comportamiento del mapeo discreto en régimen caótico pero hasta cierto valor del exponente de yapunov.

El exponente de Lyapunov es una herramienta importante corno indicador de la predictibilidad de una serie de tiempo, donde no se tiene el modelo matemático que la caracteriza .

AGRADECI MIENTOS.

Se agradece la colaboración del lng. Hugo González Hemández, M.C. Esther Vargas y al grupo de Redes Neuronales del Laboratorio del Centro de Investigación para el desarrollo de este proyecto.

REFERENCIAS

1.- Bal< P. & Chen K. ''Self Organized Criticability". Scíentific American. {U.S.A.]. January. (1991) 2.- Dubois M., Aften P. & Bergé P. "El orden Caótico". Mundo Científico. Vol. 7 No. 68. (1986)

3.- Peters. E. Chaos and Order i n the Capital Markets. John Wíley & Sons, lnc. ¡U.S.A.]. (1991).

4.- Box G. & Jenkins G. Time Series Analysis Forecasting and Control. Holden-Oay Series in Time Series Analysis. (1970).

5.- Gardner W. lntroduction to Random Processes with Apolications to Signals and Systerns. (U.S.A .]. MacGraw Hill. (1990).

6.- Kean, J. ."Chaos Theory and Neural Network Analysis". Technical Analysis of Stocks & Comrnodities, (U.S.A.]. June. (1992).

7.- Fishrnan, M ; Barr, D. & Loick, W."Using Neural Ne1s in Market Analysis". Technical Analysis of Stocks & Commodities. [U.S.A.J. April. (1991)

8.- Chakraborty K., Mehrotra K, Mohan K & Ranka s. "Forecasting the Behavior of Multivariate Time Series Using neural Networks". Neural N etworks, Vol. 5 pp. 961-970. (1992).

9.- Mead W., Jones R., ee Y ., Bames c. Flake G.. Lee L., & O'Rourke M. "Using CNLS-Net to Predict the Makey-Glass Chaotic Time Series . CNLS News!etter. Center for Nonlinear Studies Los Alarnos Na1i onal Lab., [U.S.A.J. No. 69 August (1991).

1O.- Farmer J . & Sidorowich J. "Predicting Chaotic Time Series . Physical Review Letters. Vol.

59 No. 8. (1987)