CONTROL DE UN SISTEMA NO LINEAL DE SEGUNDO ORDEN EN RÉGIMEN CAÓTICO
Julio.
E. Lago-Canosa; Pedro C. Estrada-Gutiérrez
y
Hugo G. González Hemández
RESU
MEN
En la actualidad, el estudio de sistemas no lineales ha ido aumentando a partir del descubrimiento del fenómeno de caos. Recientes trabajos demuestran
la presencia de este fenómeno en sistemas muy sencillos. En algunos casos, se requiere que el comportamiento caótico de un sistema sea
regulable,convergiendo a un punto fijo o que se comporte como otro sistema siguiendo una trayectoria específica . En el presente trabajo se muestra el
control para un sistema no lineal de segundo orden en régimen caótico, regulando la salida alrededor de un punto fijo con acciones pequeñas de control
sobre un conjunto de parámetros accesibles. El sistema caótico a controlar es el mapeo de Hénon y la técnica de control empleada es una
retroalimentación no lineal de estado. Se presenta una comparación entre retroalimentación lineal y retroalimentación no lineal del estado. También se
presentan resultados computacionales y una implementación electrónica del sistema y el control.
INTRODUCCIÓN
Un sistema caótico es un sistema determinista que exhibe un comportamiento aparentemente aleatorio. El fenómeno caótico se ha reportado en diferentes
disciplinas como astronomía, biología, ingeniería y varias otras. Una de las principales características de un sistema caótico es que puede describir
una dinámica compleja con pocas ecuaciones no lineales determinísticas. Estas ecuaciones, que pueden tener una estructura simple, pueden ser usadas
como modelos para predecir comportamientos complícados.
En algunas áreas de la ingenieria, la dinámica caótica debe ser evitada en et diseño. De aquí que: sea importante el estudio de procedimientos para
controlar sistemas caóticos (ya sea para producirlo o para eliminarlo). Por ejemplo, Vincent & Yu en 1991 [1) han aplicado diferentes leyes de
control a las ecuaciones de Lorenz. [2). El objetivo es convertir el comportamiento en estado estable de un movimiento caótico a un punto de
equilibrio. La dinámica de las ecuaciones de Hénon es muy compleja y ha sido estudiada desde hace ya varios años: sin embargo sus propiedades de
control no han sido analizadas del todo. En la última década. el diseño de leyes de control por retroalimentación para sistemas no lineales ha
experimentado un mayor desarrollo. Debido a la aplicación de conceptos matemáticos de la Geometría Diferencial, ha sido posible diseñar leyes de
control que transforman un sistema no lineal en uno lineal. ES1as técnicas han sido desarrolladas para sistemas continuos. En el presente trabajo se
exponen dos técnicas. una lineal y otra no lineal. para el control de las ecuaciones de Hénon. Se presentan los resultados de la simulación en
computadora y una implementación electrónica del sistema y el control.
DESARROLLO
La planta analizada es descrita por las siguientes ecuaciones [3):
xn 1 = Ao - X + Byn + p
y0· 1 = x,, (1)
Para el régimen caótico se tienen A0 = 1.4 , B = 0.3.


,...
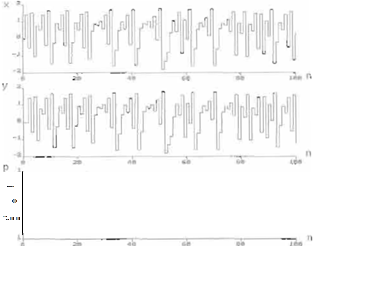
FIG 1 Sistema sin control

Para este caso el sistema se línealiza alrededor de un punto fijo del sistema. Los puntos fijos del mapeo de Hénon se obtiene resolviendo las
siguientes ecuaciones:
X = A 0 - x
Y = X
+ By
(2)
lo que da como resultado:
0.8839
XF = YF :::: {-1.5839 (3)
linealizando el sistema se tiene:
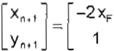
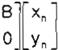 (4)
(4)
el cual, se evalúa en los puntos fijos obtenidos (3) y se calculan sus valores propios:
!..u = (-1.9237, -4.3926}
As = ( 0.1599, 0.0920)
y
vectores propios:
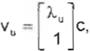
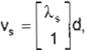
 con c,d e 9t-{O}. En este caso se aplica un método de Geometría Diferencial desarrollado por A. lsidori (4]. A partir de los vectores propios se
calculan vectores unitarios:
con c,d e 9t-{O}. En este caso se aplica un método de Geometría Diferencial desarrollado por A. lsidori (4]. A partir de los vectores propios se
calculan vectores unitarios:
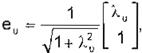
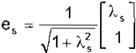
dados x0=(1, O)T, y0=(0,1)T. entonces:
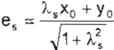
A..,Xo + Yo .
-
-
-·--
u v1+ J.. ·
Posteriorment e se definen fs y fu que son vectores de la base dual. es decir:
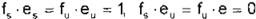
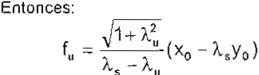
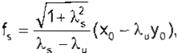
donde:
El control queda [5]:
un = e n
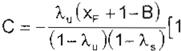
y Sn = [;:]-[ :]
es decir:
e=(1.2405 -0.1983]
Caso No Lineal:
En el caso de que se pueda emplear una retroalimentación no lineal se tiene el control:
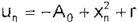
el cual línealíza el sistema de la siguiente forma:
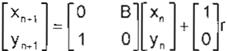
Este sistema se puede regular hacia un punto de equilibrio arbitrario solo moviendo la referencia r constante. Para seguimiento de modelo no se puede
emplear este método ni algún otro.
RESULTADOS


} \,,
Caso L
ineal
En la siguiente figura se muestra el sistema con control:

"
:·:¡
.: l
 y ;:>.';1 -
y ;:>.';1 -
.,.......
o •
"·
... 2" n
a - n
 IJ i r- lit
IJ i r- lit
" U> ..._ n
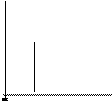
FIG. 2 Sistema con control lineal
Como se observa de la figura 2 el sistema se regula alrededor del punto de equilibrio llegando aproximadamente en 8 unidades de tiempo. A fin de
analizar los transitorios simulamos el sistema para una señal de control acotada. En la Fig. 3 se muestra el sistema con un control PE[-0.01. 0.01).
X
,.
 : íillílr iíl {{
: íillílr iíl {{
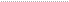 -:¡.,,
-:¡.,,
.;,iJ---,,----.;i, ---"".-- j n
.E-3
 1
1
'"...,...,,.l.Ll.U'=c...u2.¡.u
..L. ll"-'-"-r-''-- r.1. ---.," ---11.1., n
FIG 3 Sistema con control acotado P e [-O Oí 0.01]
Se puede observar de esta última gráfica que existen transitorios caóticos cuando la señal de control es acotada. En algunos casos es
necesario acotar el control ya que puede ser demasiado violento o muy grande en magnitud.
Caso No L
ineal


Para el caso No Lineal los resultados se muestran a continuación. Para er caso no lineal se tiene una convergencia ligeramente más lenta para el
sistema sin acotar la señal de control (Fig. 4). En la figura 5 se muestra la respuesta del sistema ante una señal acotada P E (-0.01. 0.01).

 V
V
"é.·ª6 '
.....
Cl..Z
1 · -· ---11
"
' "'
:: _I
8.G
-c."i=- ----------- --- n
ó •
FIG 4 Sistema con control no lineal
Se puede apreciar que cuando se acota la señal de control es considerablemente más lenta la convergencia hacia el punto fijo.
X i!IM "
y
_:Ii tr 1-
·_:;:::" lml
111" lll
2 lílll
it 4".1;1 "
FIG.5 Sistema con con1rol No Lineal acotado PE l-0.01 , O 01j
Implementación Electrónica
Para la implementación electrónica del sistema y del control se empleó un circuito basado en un multiplicador analógico AD533 [6] para elevar la señal
al cuadrado conectado a Amplificadores Operacionales para dar las ganancias respectivas [7).
En la figura 6 se muestra el sistema en régimen caótico. La figura 7 podemos observar un comportamiento periódico de periodo 3 asegurando que el
sistema implementado es caótico (8). Finalmente se muestra el sistema controlado por una señal acotada (Fig. 8)


1.-·- . _ .:_ _.. -....:. . :..... ..:... ...:... .. : _i
 1
.....::_ ..........::·-····:--···-:......:........:.......:: ....:..__1I
1
.....::_ ..........::·-····:--···-:......:........:.......:: ....:..__1I
F!G.6 Sistemz en ré;:, me . caótico

...... . .. ..., ··""' '. ....'
... ' . - -
- . . · ··· ..... .... ,. . ...... . . ..
... .... . .,........... "..""""'"
... ....... ... ......,,..... -
FIG. 7 Sistema en régimen periódico de período-3

. _ J
 ' .
' .
• .. ... p.. . ••
...................!

FIG 8 ;:,itr- r 1a controlado con lirrntes de acotamiento
CONCLUSIONES
El control de sistemas caóticos es necesario en algunos casos. En este trabajo se mostraron dos formas sencillas de controlar un sistema no lineal
discreto, en general, no es sencillo controlar un sistema caótico, específicamente si se puede añadir una entrada de control al sistema . en este caso
es muy probable que se puede implementar un control para regular hacia una referencia o al punto de equilibrio. A partir de los resultados obtenidos se
puede notar que con un control lineal sólo se puede regular alrededor del punto de equilibrio del sistema linealizado, mientras que utilizando un
control no


lineal es posible regular alrededor de una referencia deseada. En las referencias consultadas no aparece el control de un sistema caótico alrededor de una
trayectoria, éste aún es. al parecer, un problema abierto.
REFERENCIAS
(1] Vincent, T.L. & Yu, J. (1991). "Control of a chaotic system." Dynamics and Control, vol. 1, nv. 1, pp.
35-52.
[2] Hartley, T.T. & Mossayebi, F. (1992). "Classical control of a chaotic system." First IEEE Conference on Control Applícatíons, Dayton, Ohío, USA pp.
522-526.
[3] Hénon. M. (1982}. On the numerical computatí on of Poincaré Maps. Physica 50, 412.
[4] lsidori A. (1987). Lectures on Non-Linear Control, Notes prepared f or a Course at the Cart Cranz Gessellschaft (3-6
August , 1987).
 [5J Alvarez Gallegos J. (1993). Introducción a Sistemas Caóticos. Apuntes del curso. Publicación interna . CONVESTAV-IPN .
[5J Alvarez Gallegos J. (1993). Introducción a Sistemas Caóticos. Apuntes del curso. Publicación interna . CONVESTAV-IPN .
[6] González-Hernández , H. (1992). El desarrollo y estudio de sistemas caóticos. 111 Congreso Internacional de Electrónica y Comunicaciones CONIELECOM
'92. Universidad de las Américas, Puebla . 17-20 de Febrero.
[7] Estrada Gutiérrez P. & Lago Canosa J. E. (1993). control de un sistema no lineal discreto". Jornadas de Investigación ULSA. Universidad La Salle.
Noviembre de 1993.
[8] li, T. Y. & Yofke, J. A. (1975). "Period three implies chaos." Am. Math. Monthly 82, 985.
![]()
![]()

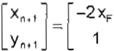
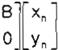 (4)
(4)
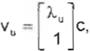
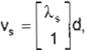
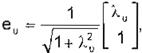
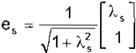
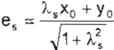
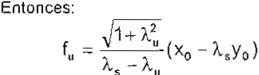
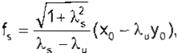
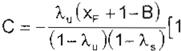
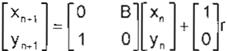
 y ;:>.';1 -
y ;:>.';1 -



 ' .
' .
