ANÁLISIS ELECTRÓNICO Y COMPUTACIONAL DE LA DINÁMICA DE UNA REO NEURONAL

ARTIFICIAL.

Hugo G.González-Hernández;Pedro c.Estrada Gutiérrez y Julio E.Lago Canosa

RESUMEN

El fenómeno caótico ha sido reportado en gran variedad de ciencias y disciplinas. Se ha definido como una situación en la que un sistema pierde sincronización consigo mismo o como un comportamiento determinista pero aparentemente aleatorio [1]. Es posible modelar una red neuronal artificial como un sistema dinámico ya sea continuo o discreto [2), para este tipo de modelos es posible simular el comportamiento de la red mediante un sistema electrónico o bien en una computadora con el programa adecuado. El poder efectuar simulaciones nos permite analizar de una manera más sencilla dicho comportamiento. En este trabajo se presenta un modelo de red neuronal de tres neuronas interconectadas. el cual fue implementado electrónicamente y simulado en una computadora personal.

INTROOUCClÓN

La actividad de una red neuronal puede ser vista como una trayectoria en un espacio de estado de dimensión 9tn. Cada punto en el espacio define una posible configuración de la red neuronal. Los valores sinápticos gradualmente cambian para aprender nuevos patrones de información por lo que la salida de la red varía con respecto al tiempo en el período de aprendizaje. La trayectoria termina cuando el sistema alcanza el equilibrio, es decir, cuando la red converge. En el caso más simple y a la vez menos frecuente, el atractor de equilibrio es un punto fijo del sistema dinámico. Las configuraciones más conocidas de redes neuronales artificiales convergen a un punto fijo. En casos más complicados el atractor de equilibrio es un ciclo límite o toroide. En general, y en la mayoría de los sistemas dinámicos, el atractor de equilibrio es aperiódico o caótico. Una vez que la red neuronal ha entrado a esta región del espacio de estado, su comportamiento parece errático sin una estructura aparente de orden. Yao y Freeman [3) en 1991 usaron modelos dinámicos neuronales y series de tiempo para argumentar que los bulbos olfatorios en los conejos procesan los olores usando atractores caóticos.

DESCRIPCIÓN

Matemáticamente se puede describir un Sistema Dinámico Neuronal mediante un sistema de ecuaciones diferenciales o en diferencias de primer orden que gobiernan la evolución en tiempo de las activaciones neuronales o potenciales de membrana. En este caso se analiza el siguiente sistema de ecuaciones en diferencias no lineales con retardo parcial:

x,(n+ 1) ;; f,[ w 21x,(n}+w 31x 3 (n)j

x2 (n+1) = f2 [x,(n)J

x 3 (n+1) = qx,(n))

(1)

donde: Xk representa biológicamente la diferencia de potencial a través de la membrana en el tiempo discreto n.

f(-) es el vector de campo que contiene las funciones no lineales de activación de cada neurona

y es de la forma:

. --

1

f' (x) =-1+ e-.(x-Q,) (2)

es un parámetro proporcional a la pendien1e de la función de activación y e denota el umbral de activación de la neurona, éstos son parámetros variables de la función de activación y se ajustan en la etapa de aprendizaje para dar la respuesta deseada.

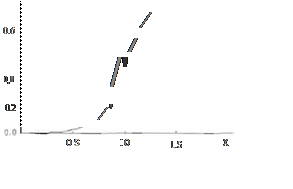
FIG. 1 Función de activación

La figura 1 muestra esta función de activación. La red neuronal está formada por un conjunto de procesadores sencillos altamente interconectados. la figura 2 muestra un procesador básico de una red neuronal. Cada neurona tiene una salida. la cual está relacionada con el estado de la neurona.

l-!il._.-OI .H­"

o••

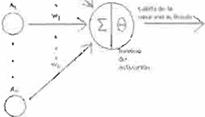
FIG.2 Procesador (Neurona)

Esta salida puede estar conectada a muchas otras neuronas, cada neurona recibe varias entradas por medio de conexiones denominadas pesos (sinapsis). Las entradas a la neurona son las activaciones de las salidas de otras neuronas multiplicadas por un peso. La activación de la neurona se calcula aplicando la función de activación fO a la sumatoria de los productos.

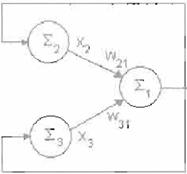
La red neurona l utilizada se muestra en la figura 3. En el trabajo que se presenta se analizó el comportamiento de esta red simple con retroalimentación de salida, encontrándose diferentes comportamientos en estado estable como puntos fijos, atractores periódicos y atractores caóticos.

Se presentan análisis de estabilldad así como resultados en simulación y también una implementación en un circuito electrónico utilizando diferentes funciones de activación.

x,

FlG. 3 Red Neuronal utilizada

RESULTADOS

Simulación en computadora

Se simuló la ecuación {1) para diferentes valores de los parámetros de la red usando el programa SIMCAOS [4]. desarrollado en el Laboratorio del Centro de Investigación de la Universidad La Salle. En la figura 4 se muestra la evolución del sistema para la neurona de salida en el régimen

caótico.

x,

...

·f 1 : l

í

r

i1

' J J

j

r- - '/

.r

r .J

,1

"

.. * n

FIG.4 Simulación de X 1 contra n

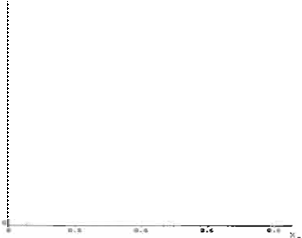
La figura 5 muestra el mapa logístico del sistema x".1( x" ).

"'"..'..

--·-""-.

/

/

/

....

...

(

..' ..

! \

/

Í

/

FIG S. Mapa Logístico Xn+1(Xn)

o .

0.2

0 ,, .. º_" J-,.-- o. -=

---e=-'

1

FIG. 6 Diagrama de bifurcaciones para la variable tt1.

En la figura 6 observamos el diagrama de bifurcaciones del sistema para el parámetro e1. Se pueden observar claramente diferentes regiones de estabilidad: puntos fijos, regiones de

comportamiento periódico, comportam iento de periodo-2. periodo-4, periodo-8,periodos nones y caos.

El exponente de Lyapunov es una medida de la sensibilidad a condiciones iniciales del sistema, si es mayor a cero en una dimensión, entonces el sistema es caótico. Para este sistema se obtuvo un

exponente de Lyapunov A.= 0.547247 para los parámetros 1=7, 2=7, 3= 13, e1=o .s, 62=0.3, 83=0.7,

w21 =1, w31 =-0.8. Estos mismos valores fueron tomados para las figuras 3 a 5.

1 mplementación Electrónica.

Con el fin de probar otro tipo de funciones de activación y de corroborar los resultados obtenidos en la simulación. se implementó físicamente un sistema electrónico que modelara la red neuronal. Para modelar la función de activación se utilizaron Ampl ificadores Operacionales. las sumas también fueron modeladas con amplificadores operacionales.

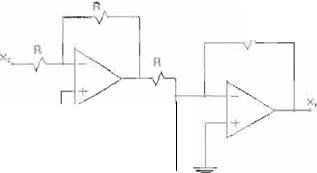
Los pesos sinápticos fueron realizados mediante resistencias (Fig. 7). Con objeto de suavizar la curva obtenida con los amplificadores operacionales se emplearon díodos y potenciómetros. La implementación de la función sigmoide se muestra en la figura 8.

R

x ,

F,tt, ---·

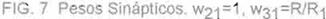
Empleando el módulo de la figura 8 se probó una función de activación truncada para observar si el comportamiento en estado estable permanecía caótico.

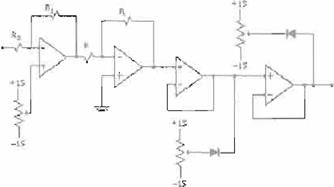
FIG, 8 Implementación de la función de activación.

Esta función de activación es mixta, es decir, tiene una parte exponencial y otra parte de función signo. Este tipo de función de activación se puede implementar fácilmente utilizando Amplificadores Operacionales , con los diodos y potenciómetros mostrados en la figura 8 se regula la suavidad de la curva. La función de activación mixta se muestra en la figura 9.

f(x)

0.8

0.6

C,'i I

0.2 /

tl.O

o.s l.G 1.s X

FIG. 9 Función de Activación truncada o mixta

El mapa logístico del sistema utilizando esta función de transferencia es como se muestra en la figura 10. Como se puede observar es una función unimodal en un intervalo. Este Mapa Logístico es equivalente al Mapeo de Tienda, el cual, se ha demostrado que es caótico [5]. Li & York en 1975 (61. demostraron que un sistema que exhiba una respuesta de período-3 es caótico para algún otro valor del

parámetro que se varía . En este caso, el parámetro que se varía es w31. Para un valor de este parámetro de aproximadamente -0.82,

FIG. 1O Mapa Logístico Función de Activación

el sistema presenta una señal de período-3 como la que se muestra en la figura 11.