SUAVIZACION DE TRAYECTORIAS PARA VEHICULOS AUTOGUIADOS
Hugo G. González-Hernández
y
M. Farias-Elínos.
Centro de Investigación, Universidad La Salle
RESUMEN
Existen varías aproximaciones para la planeación de vehículos autogutados. uno de ellos es la aproximación del mapa de carreteras. Este método consiste
en encontrar todos los caminos posibles evitando los obstáculos del lugar. La selección del camino no tiene continuidad en la primera derivada , esto
significa que hay puntos en el camir:io donde la primera derivada no existe. Para evitar este problema nosotros aproximamos el camino utilizando 8-splines. La trayectoria resultante tiene la primera derivada continua en todos los puntos del camino.
ABSTRACT
There are many approaches to path planning for autoguided vehicles, one of them is the Roadmap approach. This method consists on finding all possíble
paths avo1díng obstacles in a room. The chosen path often has not continuous first derivatíve, this means that there are points in the path where the
first derivatíve does not exist. To avoid this problem we approximate the path using 8-sp/ines. The resulting trajectory has continuous first
derivatives in all points of 1he path.
INTRODUCCIÓN
Los 8-splines cúbicos son una clase de función de curvas definidas sobre intervalos discretos, donde cada coordenada de la primera y
segunda derivada son continuas sobre el segmento de la curva y sobre los nodos de control que son parte de la curva. El segmento de la curva es
calculado a partir del conjunto de puntos que son los vértices del polígono característico de la curva. Los puntos del polígono dependen de la
selección de los puntos. la localización de los vértices del pol gono característico pueden encontrarse por iteraciones del algoritmo de Yamagushi [1]
o por el algoritmo de solución matricial de Barsky y Greenberg (2).
Después de dar la curva como entrada, la primera estrategia es definir los puntos nodos sobre la curva. La distancia entre estos puntos no
necesariamente debe ser igual. Se han propuesto varios métodos para definir los puntos nodos y para la cunstrucción de la curva . Shirai (3) propone
calcular el ángulo entre las lineas P,.1P, y P,P,,.1 . Todos
los puntos P, para los cua les este ángulo es menor que algunos valores de umbral son eliminados . Este método puede guardar pocos
puntos para una parte recta de la línea, pero guarda muchos para una curvatura constante. El código de cadena utiliza la técnica de seguimiento de
puntos vecinos en una de las ocho direcciones discretas.
Ninguno de los métodos mencionados anteriormente da una selección de puntos suficientes para preservar la forma general y local de la curva a
reproducirse como se requiere en este problema. El algoritmo descrito en este trabajo fue concebido a partir de ideas de Brice y Fennema(4]. y
Guzman(S].
Teniendo los puntos nodo, pueden ser usadas varias clases de splínes y otras curvas. El 8-spline cúbico es usado a menudo para
representar curvas. en nuestro caso, aproximaremos un conjunto de puntos mediante una curva seccionalmente polinómica.


DETECCIÓN DE PUNTOS NODOS
Para poder suavizar la trayectoria es necesario llevar a cabo primero una detección de esquinas o nodos. Esto es esencial para la descripción de curvas
planas que será utilizado para representar la trayectoria. La definición de esquina es relativa pero podemos entenderla como una discontinuidad. Con
esta percepción en mente podemos identificar una gran cantidad de esquinas en la trayectoria a suavizar. Mientras una función polinomial a pedazos como
un 8-sp/ine es suficientemente flexible para tener una cúspide aguda, el comportamiento de la curva cerca de la cúspide es muy forzada, por
eso trataremos de no modelar esas esquinas con cúspides. Con la suposición de que las terminaciones de los curvas son esquinas. nuestro método es
tratar cada segmento de curva entre pares adyacentes de esquinas como una curva elemental a ser ajustada y representada por una función B-spline con la condición de que el punto terminal sea interpolado. Ésto asegura que las curvas reconstruidas sean continuas en las posiciones
de las esquinas.
Se ha adoptado un método convencional (6) para detectar esquinas de una curva para facilitar el proceso de la aproximación por 8-splines. este método
se describe a continuación:
Considere un segmento de curva con n+1 puntos digitalizados {(x,.y,)J;0 , como los
puntos terminales ( x 0 ,y 0 ) y ( x,,.yn ) se suponen esquinas ( la curvatura en estos puntos se fija en
cero), trataremos de encontrar otras esquinas a partir de los puntos (x, .y,) para i=1.2,...,n-1. En cada uno de
estos puntos. la curvatura digital es evaluada de la siguiente forma:
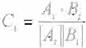
donde:
A1 -:: ( J: , ,j -J., .J': 1 - } , )
con i+j = n en caso de que i+j > n e i-j = o en caso de que í-j < O. En
este caso " · " denota el producto interno de los vectores y IXI denota la longitud o nomia euclidiana del vector X. Si C1, i =1,2,...,n-1. es
un máximo de Ck, para í-j2 k i+j2 con C1 >-C2, tomamos el punto ( x,.y,) como una esquina. Se
fijan experimentalmente las constantes j = 3, j2 == 4 y C2 = O.5.
I
NTERPOLACIÓN DE LA CURVA
Para realizar la interpolación de la curva con B-splines de los puntos nodo y entre los pares de esquinas detectadas en la sección pasada
utilizamos una aproximación tomada de Lozover y Preiss [7) la cual fue originalmente propuesta por Yamaguchi [8). Aquí un conjunto de vértices de
control se calcula a partir de un conjunto de nodos para definir la curva B-sptíne que pasa por los r.odos entre cada par de esquinas
adyacentes. Dado un conjunto de m+1 vértices de control V,, donde í=O, 1,...,m, una curva 8- splíne Q(u) es
definida seccionalmente como:
Q
(
11
)
= ¿r 1b,.( u). 11 '=- ¡O I J. i = 1....,m - 2 (2)

donde las funciones a-spline base b,{u) son:
1
-
.311 - ]11
?
-
JI
h
(11 )
=
-
-
-
--
-
' 6
-f.
-
611
'.!
+311
1
h
/)
(
u)
---
-
-
6
_ ¡ .... Ju+ Jt.1 - 3u'
b
'
(
l
)
-- ----
' 6
(3)
11
3
h,(11)
=
-
- 6
Denotamos todos los puntos nodo obtenidos en la sección anterior como P;, i=1.....m-1 para el B-spline cúbico. Para llevar a cabo Ja
interpolación de estos puntos los compararemos con los puntos terminales de los segmentos de curva Q¡{u). i=1,....m-2.
Q.( 0)
=
f:
.
Q,"
2 f
/
)
= P," .'
i
= l.. ..m-
2
dándonos un conjunto de ecuaciones lineales para los vértices de control B-splfnes:
v,
1
+ .¡ + r·:.1 =- 61 . 1 = l.. .. .. (6)
para completar el conjunto de ecuaciones se determinan las siguientes condiciones arbitrariamente para asegurar que la curvatura es cero en los
extremos de la curva:
y
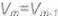
La matriz de ecuaciones resultante es diagonalmente dominante, y puede ser resuelta por métodos numéricos convencionales.
APROXIMACIÓN
DE LA CURVA
Para aproximar una curva utilizando B-splines es necesario solamente considerar que los puntos esquina encontrados en una de las secciones
anteriores son los vértices del polígono característico utilizados en la ecuación (2).
SUAVIZACIÓN DE TRAYECTORIAS
Una imagen aérea de un recinto al momento de ser digitalizada generalmente tiene ruido o irregularidades debido al proceso de digitalización, para ello
es necesario realizar varias operaciones de preprocesamiento, conocidas principalmente como filtros, los cuales se encargan de disminuir el ruido y
tener una imagen nítida y confiable sobre la cual se pueda trabajar. Una vez realizado dicho filtrado la imagen es binarizada, bajo un umbral. quedando
en negro los obstáculos que existen y en blanco el camino libre por donde se puede pasar el vehículo. para posteriormente obtener el mapa de carreteras
o caminos posibles por donde puede pasar el vehículo.
Para la obtención de dicho mapa de carreteras se recurre a las técnicas de engrosamiento de objetos , esqueletización. concatenación, podado y
obtención del mejor camino para llegar de un punto inicial a


un punto fina!. Antes de la obtención del mapa de carreteras es necesano dar un márgen de seguridad al paso del vehículo, para lo cual los obstáculos
son engrosados o dilatados utilizando el radio de un círculo que circunscribe al vehículo como parámetro.
 Para la obtención del mapa de carreteras se utiliza la esqueletización, por medio de la cualse tiene una representación de las áreas libres del
recinto, cuyo grosor no es mayor a la de un pixel. a esto se le conoce como el esqueleto, en el cual cada rama representa un posible camino por donde
puede pasar un vehículo. Posteriormente a este esqueleto se le unen los puntos de inicio y final de la trayectoria del vehículo. El siguiente paso a
realizar es el podado o borrado de las ramas que no son útiles dentro del recorrfdo del robot. La figura 1 muestra el mapa de carreteras para un caso
de prueba.
Para la obtención del mapa de carreteras se utiliza la esqueletización, por medio de la cualse tiene una representación de las áreas libres del
recinto, cuyo grosor no es mayor a la de un pixel. a esto se le conoce como el esqueleto, en el cual cada rama representa un posible camino por donde
puede pasar un vehículo. Posteriormente a este esqueleto se le unen los puntos de inicio y final de la trayectoria del vehículo. El siguiente paso a
realizar es el podado o borrado de las ramas que no son útiles dentro del recorrfdo del robot. La figura 1 muestra el mapa de carreteras para un caso
de prueba.
 FIG.1 Mapa de Carreteras.
FIG.1 Mapa de Carreteras.
Una vez obtenido el mapa de carreteras con los caminos posibles por donde puede pasar el vehículo desde su punto de inicio hasta su punto final, se
entra en una etapa de optimización de la trayectoria. la cual consiste en obtener la mejor ruta por donde puede ir el vehículo desde su punto de inicio
hasta el punto final de la trayectoria sin ningún problema; para dicha optimización se toma en cuenta el ancho mínimo del camino, la longitud mínima y
el ancho promedio (9). Por último se suaviza la trayectoria obtenida.

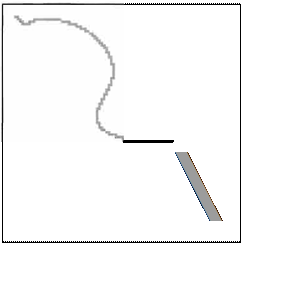
(a)
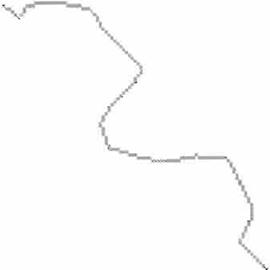 (b)
(b)

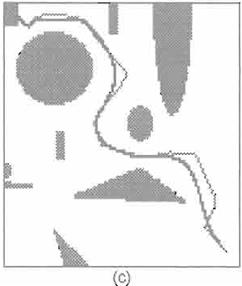
FIG. 2. {a) Trayectoria sin suavizar, (b) trayectoria suavizada,
(e) ambas trayectorias.
REFERENCIAS
1. Yamaguchi , F. "A new curve fitting method using a CRT computer display". Computatíonal Graphics and lmage Processing. Vol.
7, pp. 425-437 (1978).
2. Barski, 8.A. y Greenberg, D.P. Determining a set of B-spline control vertices to generate an interpolating surface. Computational Graphics and /mage Processing. Vol. 14, pp.203-226 (1980).
3. Shirai, J. "A hierarchical program for recognition of polyhedra. Bu//. Electrotechnic Laboratory of Japan. Vol. 36,
pp. 655-672 (1972).
4. 8rice, C.R. y Fennema, C.L. "Scene analysis using regions". Artificial lntel/igence. Vol. 1, pp. 205- 226. (1970).
5. Guzman, A. "Analysis of curved line drawings using context and global information". Machine lntelligence. Vol. 7, pp.325-375 (1972).
6. Sekita, l.; Toraichi, K.; Morí, R; Yamamoto, A. y Yamada, H. Feature extractíon of handwritten japenese characteres by spline functions for relaxation
matching". Pattem Recognition, Vol. 21, pp. 9-17 (1988).
7. Lozover, O y Preiss, K. •Automatic construction of a cubic B-spline representation for a general curve". Computational Graphics, Vol. 7(2),
pp.149-153. (1983).
8. Yarnaguchi , F. "Curves and surfaces in computer alded geometrlc design". Springer, Berlín. (1988).
9. lbarra-Zannatha, J.M.; Sossa-Azuela, J.H. y González-Hernández, H.G. " A new Roadmap approach to automatic path planning for mobile robot navigation . 1994 IEEE lntemational Conterence on Systems, Man and Cybemetics, San Antonio TX. Octubre, 2-5, 1994.
![]()

 Para la obtención del mapa de carreteras se utiliza la esqueletización, por medio de la cualse tiene una representación de las áreas libres del
recinto, cuyo grosor no es mayor a la de un pixel. a esto se le conoce como el esqueleto, en el cual cada rama representa un posible camino por donde
puede pasar un vehículo. Posteriormente a este esqueleto se le unen los puntos de inicio y final de la trayectoria del vehículo. El siguiente paso a
realizar es el podado o borrado de las ramas que no son útiles dentro del recorrfdo del robot. La figura 1 muestra el mapa de carreteras para un caso
de prueba.
Para la obtención del mapa de carreteras se utiliza la esqueletización, por medio de la cualse tiene una representación de las áreas libres del
recinto, cuyo grosor no es mayor a la de un pixel. a esto se le conoce como el esqueleto, en el cual cada rama representa un posible camino por donde
puede pasar un vehículo. Posteriormente a este esqueleto se le unen los puntos de inicio y final de la trayectoria del vehículo. El siguiente paso a
realizar es el podado o borrado de las ramas que no son útiles dentro del recorrfdo del robot. La figura 1 muestra el mapa de carreteras para un caso
de prueba.


 (b)
(b)
