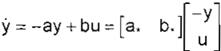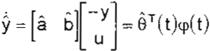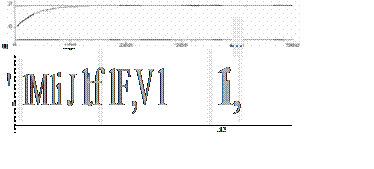IDENTIFICACIÓN DE LOS PARÁMETROS DE UN SISTEMA DINÁMICO UTILIZANDO UNA SEÑAL CAÓTICA EN EL REGRESOR.

Hugo G. González-Hernández, María del Carmen Lule Carplnteyro y Pedro Estrada Gutiérrez

Centro de Investigación, Universidad La Salle.

RESUMEN

Para aplicar métodos de gradiente y minimos cuadrados en la estimación de parámetros es necesario que las señales medibles o generables del regresor sean de excítación persistente, es decir. que tengan suficiente cantidad de frecuencias para excitar todos los modos de respuesta del sistema a identificar. Tanto el ruido blanco como la señal caótica son señales de excitación persistente. En este trabajo se presenta una comparación de estas dos señales usándolas como parte del regresor para la identificación de los parámetros de un sistema dinámico.

ABSTRACT

To apply least-square and gradíent algoríthms for parameter estímation, the input and meassurable signals in the parameterization are needed to be of persistent excitation; this means that these signals are capable to stimulate all system modes. This could be posible if signals have enough number of frequencíes . White noise and chaotic signals are of persistent excitation . The current studies, shows a comparison of both signals in the regresor (input and output signals) to identify system parameters.

INTRODUCCIÓN

El concepto de modelo matemático es fundamental en ingeniería y en otras disciplinas. Un modelo se puede obtener por razonamientos físicos o analizando datos experimentales del sistema. En este último caso, la habilidad para obtener un modelo preciso es limitada por la presencia de fluctuaciones aleatorias tales como perturbaciones no medidas y errores de medición. El propósito de estudio de la Identificación de parámetros es precisamente el de obtener modelos matemáticos a partir de observaciones ruidosas del sistema. Las técnicas desarrolladas para llevar a cabo esta identificación son muchas y muy variadas [1]. algoritmos de Minimos Cuadrados, algoritmos Gradiente. algoritmos de Máximo de Verosimilitud, etc. Todas ellas requieren de una parametrización previa del sistema, posterior a esta parametrización se puede aplicar cualquiera de estos métodos. Para excitar todos los modos del sistema se requiere que la entrada sea de excitación persistente, es decir, que contenga suficientes frecuencias para identificar los parámetros del sistema Una señal caótica es una señal de excitación persistente [2]. En este trabajo se muestra la identificación de los parámetros de un sistema eléctrico mediante un algoritmo Gradiente y empleando primero una señal de ruido blanco y posteriormente una señal caótica en el regresor. Se comparan resultados y se concluye a partir de éstos.

DESCRIPCIÓN DE LA PLANTA E IDENTIFICACIÓN

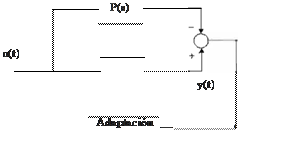
Considérese la planta mostrada en la figura 1:

y(c)

._ c(t)

FIG. 1 Planta para P(s) estable y u(t) seccionalrnente continua.

Sea:

y(t) "" q>T(t)9. (1)

la parametrización de la planta P(s) donde <pT(t) es el regresar y contiene la entrada y las funciones medibles necesarias par la identificación, e. es el vector de parámetros reales (desconocidos) de la

planta. Se tiene:

y(t) = q¡'( t )ó( t) (2)

donde y( t) es la variable a estimar, y el vector é(t) contiene los parámetros estimados. Considérese la ecuación ·de error:

e(t ) = y( t)- y(t) (3)

El objetivo es obtener una ecuación que nos permita describir la evolución de los parámetros estimados de tal forma que se minimice un cierto índice de desempeño dado:

J = J(e:( t)) (4)

un algoritmo gradiente se puede expresar como:

.:. oJ

9(t) = -y A­

OO (t)

'Y > o (5)

Existen varios índices de desempeño a minimizar,de los cuales emplearemos el siguiente:

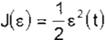(6)

Se tiene que:

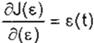
y como

s(t) = c.pT (t)B(t), é(t) = é(t) - e.

entonces:

é( t) == -re( t)cp(t) (7)

para y > O.

El algoritmo es estable. La prueba de estabilidad se encuentra en la referencia [3].

En forma recursiva:

é(t + ót) = S(t) T L\t(-y€ (t)cp( t) ) (8)

SIMULACIÓN

Para la simulación se empleó una planta de primer orden de la forma:

b

y(t) = - -u( t) t- d(t)

s+a

con a = 1. b = 2. d(t) = ruido blanco con media cero y dispersión 0.1. El ruido blanco modela errores de medición.

Parametrización:

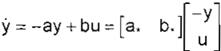
la variable a estimar está dada por:

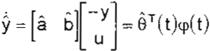
De esta forma. la aplicación del algoritmo f1) desarrollado es directa. Podemos observar que el regresor está formado por una señal generable u y una señal medible y.

A continuación se muestra la simulación usando diferentes señales para u. En la figura 2 se muestra la evolución de los parámetros para una entrada de ruido blanco con media cero y dispersión de 0.1.

4

b

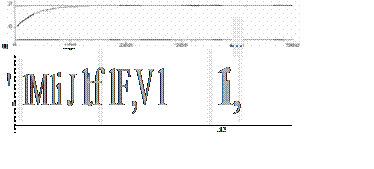
FIG. 2 Identificación de parámetros utilizando una señal de ruido blanco en el regresor.

:

·,. -... ---,,... -----;;¡.,

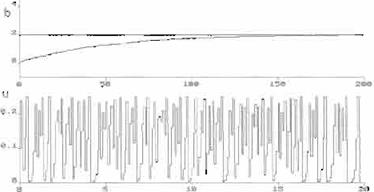
FIG. 3 Identificación de parámetros empleando una señal caótica en el regresor.

En la figura 3 se muestra una simulación para el mismo sistema, ahora empleando una señal caótica en el regresor. La señal caótica es producida por el Mapeo de May (4] descrito por:

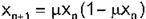(9)

Para el régimen caótico µ=4.

Comparando ambas simulaciones se puede observar claramente que la convergencia de los parámetros es considerablemente más rápida cuando se aplica una señal caótica en el regresor que cuando se aplica una señal aleatoria.