DISEÑO Y SlMULACJON DEUN CONTROLADOR 01FUSO
Gabriefa Cerezo Leal y Eduardo G6mez Ramirez
Universidad de Sheffield1 Reino Unido y Centro delnvestígación, Universida La Salle
RESUMEN
Desde que surgió, hace más de 20 aos, la Teoria de Conjuntos Difusos ha evolucionado notablemente, se ha desarrollado como una colección de conceptos y técnicas que permiten trabajar con fenómenos complejos que no permiten ser analizados por los métodos tradicionales como la Lógica Bivalente
o la Teoría de Probabilidades. Actualmente, ha trascendido más allá de lo que es el desarrollo de la teoría y se han encontrado un sinnúmero de
aplicaciones, utilizándose principalmente en el control de
procesos industriales. A pesar de ser una teoría nueva, la Lógica Difusa tiene aplicaciones actualmente en diversos campos como la inteligencia
artificial, computación, robótica, ingeniería de control, toma de decisiones, sistemas expertos, lógica, investigación de operaciones, sociología,
mercadotecnia, entre otras. Es en Japón donde más se ha aplicado la Teoría de la Lógica Difusa y se han explotado notablemente sus ventajas y
flexibilidad en los diversos campos.
Este trabajo, pretende mostrar la facilidad y versatilidad de la Lógica Difusa para implantar sistemas de control para procesos industriales. Se diseñó
un controlador para un sistema hidraúlico de segundo orden. ya que este proceso se encuentra, con distinto grado de complejidad, en la mayoría de las
plantas industriales.
ABSTRACT
When appeared, more than 20 years ago, the theory of fuzzy sets has remarkable evolutionated, this theory has develop as a collection of concepts and
techniques that allows to work with complex phenomena, that it's not easy to be analyzed by the traditional methodology as the binary logic or
probability theory. Now has a trascendental development more than the development of the theory and we found an unlimited number of applications with a
main use in the control of industrial process. Althought it's a new theory, the Fuzzy Logic (FL) has application in different fields, as artificial
lntelligence, computation, robotics, control engineering, take decisions, expert systems, logics, sociology, marketing, among others. Japan is the
country where FL has found remarkable advantages and flexibility in several fields. The current study shows the easyness and versatility of the FL to
implant a
control system for industrial process. We designed a controller for a 2nd order hidraulic
system because we could find this one in most of the industrial plants.
INTRODUCCIÓN
La Lógica Difusa se fundamenta en lo que se conoce como Teoría de Conjuntos Difusos [1J. que como su nombre lo indica se basa en conceptos en los que
todo tiene un grado de pertenencia. Los números sobre los cuales se apliquen estos conceptos. dejarán de pertenecer a la lógica clásica ó bivalente, y
tomarán valores que estarán en un rango de O a 1. Estos números pueden representar cualquier


concepto que se produzca en el razonamiento humano, desde un concepto bivalente como sí o no, hasta un concepto ambiguo como muy, mucho, no tanto, un
poco,etc.
En las plantas modernas, se ha utilizado el control por medio de computadoras [2,3), la planta se modela y se calculan Jos parámetros de control
necesarios para controlar dicho proceso. Los modelos de las plantas son en realidad aproximaciones del proceso real y en muchos casos el esfuerzo
requerido para desarrollar el modelo matemático se convierte una tarea muy difícil y por consiguiente consume mucho
tiempo de procesamiento.
Las estrategias de control han evolucionado notablemente a partir del controlador PID tradicional [4]. sin embargo, en algunos casos la estrategia
puede ser buena pero si el modelo del proceso no es el adecuado, el control del proceso no tendrá resultados óptimos. Gracias a las grandes ventajas y
flexibilidad con las que cuenta la Lógica Difusa para expresar conceptos y acciones ambiguas [5]. surge
el control Difuso (FLC)1 como una buena opción para fa solución de dichos problemas. (6-9]
En este trabajo se presenta la descripción deldiseño de un controlador difuso y su implementación para el control de una planta de segundo orden. El
artículo está estructurado de la siguiente forma: primero se analizan algunos conceptos básicos sobre lógica difusa (10-12]. luego se analizará cuál es
la metodología para diseñar un control difuso y su comparación con control clásico (PID2). por últímo se presentarán los resultados y las conclusiones
.
CONCEPTOS GENERALES DE LÓGICA DIFUSA
Número Difuso
se dice que un número N es difuso si N es un conjunto normalizado y convexo que pertenezca a los números reales, tal que:
a) Exista exactamente un elemento E rn con un grado de pertenencia µN(x0) = 1. Donde Xo se conoce como valor medio de N y,
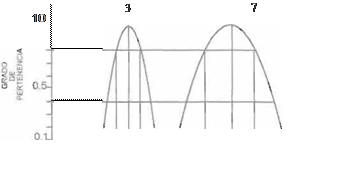
b) Que la función de pertenencia µN(x) sea continua por partes. En la figura 1 se muestran las funciones de pertenencia para los números difusos 3 y 7.
 o
o
1 2 3 4 5 6 7 8 9
Fig.1 Números Difusos 3 y 7

1Fuzzy Logic Control
 2 Proportional Integra l Derivative Controller
2 Proportional Integra l Derivative Controller
Variables Lingüisticas
Las variables lingüísticas son aquellas cuyos valores no son números sino palabras u oraciones en un lenguaje natural o cotidiano, por ejemplo un
adjetivo.
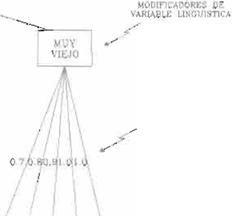
Si se considera la variable lingüística EDAD, se puede definir como se muestra en la figura 2
!EDAD
-,-......
- .:.------.-.···----·.- _.;,.
1 !llY J('tVH• Vl 1'"1()
\'A..
AvU
'
?
- 1.llicJ1s:1c

 -1,J t.\C:N --, _J
-1,J t.\C:N --, _J
!i·
\
t
I
\. w/;,/
IJ · ,
H• ·a r. t v
¡
/
O¡, l tlJ.I ";
(;RM>(JS or
r'ERTEJltNl'fA
(·
¿,
 ¿ fil L
¿ fil L
o 25 '10 '.') 40 ·11> 60 55 11
 1---1---;
1---1---;
o5 70 76 60 8 90

Fig.
2. Variable Lingüística EDAD
Fu
nciones
de Pertenencia
Las funciones de pertenencia µ(x) son funciones en x que definen el Conjunto Difuso que representa a la variable lingüística. Estas funciones
determinan el grado de pertenencia de un elemento al conjunto difuso, por lo que se representan:
µA(x) = f(x) y representa el grado en que x E A
Las funciones de pertenecía pueden estar definidas de distintas maneras, las más comunes y más sencillas de procesar son aquellas definidas con números
difusos del tipo triangular o bien trapezoidal. Las únicas condiciones que deben cumplir son:
a)
Que su rango esté normalizado de [O,1] y,
b)
Que entre más cumpla el elemento del conjunto las características que definen la variable lingülstica, más cercano sea su grado de pertenecia a 1.
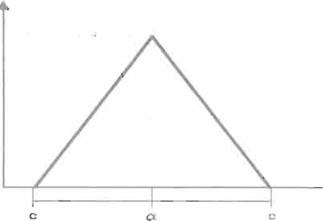
Un ejemplo de función de pertenencia es el que se muestra en la siguiente figura:

 µA. (x)
µA. (x)

o
 "A(a) _ l - 1 X a 1
"A(a) _ l - 1 X a 1
Fig. 3 Funciones de Pertenencia. definida por números difusos triangulares.
Reglas Si ... Entonces ...en Lógica Difusa
Antecedente : Consecuente : Conclusión :
Este jitomate está un poco rojo
Si un jitomate está rojo, entonces está maduro Este jitomate está un poco maduro.
Se considera el consecuente del ejemplo utilizado anteriormente; Consecuente : Si et jitomate está rojo ,está maduro
Los conceptos "jitomate está rojo'' y "está maduro", se pueden expresar como Conjuntos Difusos. sin embargo, como tales, representan conceptos
independientes. Es la claúsula Si... entonces... la que los relaciona en un solo concepto. Esta claúsula está determinada por la relación difusa que
dará como resultado el Conjunto Difuso deseado.
Con esto se puede decir, que todas las acciones que desempeña el ser humano en su vida cotidiana. se pueden expresar como un conjunto de reglas Si...
entonces .....
Fuzificación y Defuzificación
Se conoce como proceso de "fuzificación", al hecho de aplicar la Lógica Difusa al conjunto de reglas Si...entonces... que determinan una acción y
posteriormente relacionar todas estas reglas por medio de una suma lógica. Este proceso de tuzificación siempre, va de las premisas o condiciones a la
conclusión y, posteriormente pasa por la suma lógica. Hasta aquí se obtiene un resultado que será un número difuso. Para convertir este número difuso a
un número ordinario (que puede ser un valor normalizado).
:;egún la salida deseada del proceso, es necesario "defuzificarlo" del inglés "deffuzzify", que comúnmente se entendería como quitarle lo difuso al
resultado. (13]
En la figura 4, se muestra esquemáticamente un proceso de inferencia por medio de los procesos de fuzificación y defuzificación.
Como se puede ver tas reglas son independientes unas de otras y por lo tanto se pueden procesar de


manera paralela, hasta el momento en el que se relacionan por medio de la suma lógica.(14}
REGLA 1

ENTRADA(S) ANTECEDENTE CONSECUE::NTE

ENTRADA(S)

 DEFUZfFlCAClO:'.
DEFUZfFlCAClO:'.

..',/;$'
ru:GU n ..'b

ENTRADA(S) ANTECEDEN'l'E CONSECUENTE


" Y " lo¡¡Joo
Fig. 4 Proceso de Inferencia Difuso
CONTROL DIFUSO
Los controlador es Difusos son distintos a los controladores clásicos, ya que no necesitan de un modelo o algoritmo matemático que determine cómo las
salidas dependen de la entrada para alcanzar el punto de ajuste deseado.
Los Controladores Difusos, representan elcomportamiento ambiguo de un sistema o proceso mediante un conjunto de reglas Si... Entonces ... que llevarán a una conclusión Difusa la cual, se tendrá que defuzíficar .
El diagrama básico de un proceso controlado mediante Controlador Difuso es el que se muestra en la figura 5.
 -
+
-
+
cir.,:rpn¡ r11 n -=r.1
Fig. 5 Diagrama de Bloques Sistema de Control Difuso
La estrategia de control de un Controlador Difuso reside en el conjunto de reglas que determinarán el comportamiento tanto del controlador como del
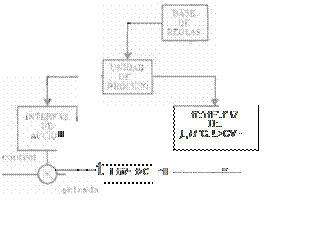
sistema , estas reglas están basadas en la base de conocimientos de un operador experto del proceso . En la siguiente figura se presenta el diagrama de

bloques de un Controlador Difuso .


DIF"USOS L{-==:J
OBSERVAC1Cl<'ES
{VAllll!:Bl.f.S) __ ,
GD\UWl
COliJll't1'0S
1 e.ASE: D RWUS
('1.-.z:FlC/ICIO )
'"--- ---
.\CC!ON
OEFUZ:flCACIO.N , - DE
CONTROL
!unc).o.ne.
de
p
_
.
.
..r-Let:IC.Oei.a
DlAGRAMA DE BLOQUES
CONLROWX>R Olf'USO
Fig. 6. Controlador Difuso
Del diagrama de bloques anterior, se tiene que el algoritmo de un controlador difuso puede expresarse como sigue:
1.
Definir las variables de entrada y de control, así como los estados intermedios que se deben observar y controlar.
2. Definir los conjuntos difusos que expresarán las observaciones y acciones del proceso, es decir, determinar las variables lingüísticas y funciones
de pertenencia .
3. Diseñar la base de reglas, que determinará cuáles reglas se activarán bajo qué condiciones
4.
Diseñar la unidad de procesamiento difuso, ésta proporcion.srá la salida difusa.
5.
Determinar el método para quitarle lo difuso a la salida , es decir, defuzificar la acción de control correspondiente.
El siguiente cuadro comparativo, muestra las principales diferencias entre el algoritmo para un Controlador Clásico y un Controlador Difuso.
En un controlador PID convencional, lo que se modela es el sistema o proceso a controlar, mientras que en un Controlador Difuso la parte esencial son
las acciones de control dadas por el operador experto .
En el primer caso, el sistema se modela por un conjunto de ecuaciones diferenciales, lo cual no siempre es fácil o incluso posible; y la solución de
las ecuaciones diferenciales indican al PID como ajustar sus parámetros para un comportamiento determinado. En un Controlador Difuso, estos parámetros
ya están dados en la base de reglas generada por el operador experto.



|
Algoritmo de Control PID Discreto
u(kT) = kpe(kT) + k¡e((k - 1)T]
+ kd e[(k- 2) T] +u((k - 1)T)
|
Base de reglas Construir Matriz Difusa
1:. R ROH
|
|
Operaciones Necesarias
Conocer los parámetros de sintonización, es decir las constan1es kp, kd y ki, lo cual se hace por métodos como el de
Ziegler-Nichols, es muy Importante sintonizar óptimamente el controlador, si no, los resultados no seran los deseados Para ello, es
necesario obtener la respuesta en lazo
abierto del sistema.
Calcula el error e, a partir del nivel en TQ2.
Aplica algoritmo de control PID discreto, para ello requiere las constantes de sintonización y conocer el tiempo de muestreo.
Determina la acción cie control
|
Operaciones Necesarias
No se requiere ningun cálculo previo, n1 modelo del sistema , ni parámetros, ni hacer nmguna modificación manual al sistema. Tampoco se
requiere conocer ninguna respuesta del sistema en lazo abierto o antes de controlarlo. En este caso se obtuvo la respuesta sin
controlador por fines comparat1vos.
Lee el nivel en TQ2 y calcula error e y e' a partir de la medición anterior.
Activa base de reglas. Calcula d1stribuc16n de la salida y obtiene su centroide difuso.
Defuzifica y obtiene acción de control.
|
¿Cuándo usar un Controlador Difuso?
A pesar de las ventajas. arriba mencíonadas, no siempre el diseñar un Controlador Difuso es la mejor solución al problema de control (15].
Se recomienda el uso de un Controlador Difuso, cuando las variables de control son contínuas, cuando no existe el modelo matemático del sistema o bien,
existe pero es difícíl de programar o es muy complejo para ser evaluado en tiempo real; cuando se trabaja en ambientes con ruido. o bien se requiere
implantar un procesador o sensor poco costoso. Pero, lo más importante. se recomienda cuando se cuenta con el conocimiento de un operador experto ,
quien pueda determinar tanto las reglas como los Conj untos Difusos que representen las características plenas de cada variable. [16]

J
,...\,
DISEÑO DEL CONTROLADOR POR MEDIO DE LÓGICA DIFUSA
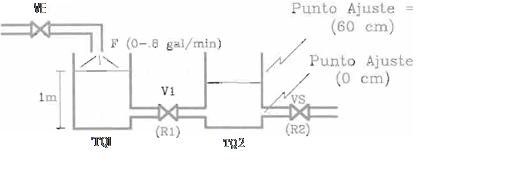
El Controlador Difuso que se diseí'lará en esta sección, es para controlar un sistema hidraúlico de segundo orden, como el que se muestra en la fig. 6.
[17,18)
Pl
anteamiento
del Problema
Se desea controlar el flujo de entrada F, para alcanzar y/o mantener el nivel de líquido deseado en el tanque TQ2.
Este nivel deseado se indicará como un Punto de Ajuste al controlador, el cual estará en un rango del 0% al 100%, dependiendo del nivel en el tanque
TQ2.
Q+q
100%
 o 3
o 3
Fig. 6
Sistema a Controlar
Definición
de los Conjuntos
Difusos
Variables Lingliistlcas
Se definen 5 variables lingüísticas para cada una de las variables del proceso. Las variables lingüísticas para el error (E) y el cambio en el error
(E') son las mismas, sólo que con rangos distintos y obviamente descripciones o representaciones distintas .
ERROR E
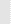 Variable Linguist1c..
Variable Linguist1c..
GN
Grande Negativo PN Pequeño Negativo Z Cero
PP
Pequeño Positivo
GP
Grande Positivo
Descripción
Na está muy por debajo de Nd Na está un poco abajo de Nd Na es igual o casi igual que Nd Na está un poco arriba de Nd Na está muy por arriba de Nd
CAMBIO DE ERROR E'
Varía
ble
Lmgüística
GN
Grande Negativo PN Pequeí'lo Negativo Z Cero
PP
Pequeño Positivo
GP
Grande Positivo
Descripción
El
tanque se vacla rápidamente Eltanque se vacía moderadamente El tanque no se llena ni se vacía
El tanque se llena moderadamente
El
tanque se llena rápidamente
FLUJO F (proporcional a la apertura de la valvula)
Variable Descripción
Lingüística
DM Disminuir Mucho DP Disminuir Poco M Mantener
AP Aumentar Poco AM Aumentar Mucho
Se requiere cerrar mucho la válvula Se requiere cerrar un poco la válvula Mantener apertura de válvula
Se requiere abrir un poco la válvula Se requiere abrir mucho la válvula
Funciones de Pertenencia
Se definen las Funciones de Pertenencia del tipo triangular, traslapadas con un traslape menor al 25%; cumplen el requisito de que entre más satisfaga
una entrada x, las condiciones que definen una función de pertenencia, su grado de pertenencia será más cercano a 1.
Son 5 los conjuntos difusos que se forman y cuentan con los rangos que se muestran en las figuras 7,8, y 9, las cuales presentan las funciones de
pertenencia para el ERROR, CAMBIO DEL ERROR y FLUJO, respectivamente.

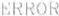
l ( \ :-; . l\ d ) ( ( 111 )
Fig. 7 Funciones de Pertenencia ERROR

 l.) \ l. (;p
l.) \ l. (;p
-·.. ·
l \ \lf3J O DCL J.:1,:LO H ( !'. )
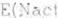 \ ' m)
\ ' m)
Fig. 8. Funciones de Pertenencia Cambio de Error

•--. .'.
3
....1.
?'
....
m.1 DP \.l . 11 .\ \
, ';-
;L.;_ --- .
-.:.:;
- .·
r.¡x JO
(
· .\ p E:' 1l1.1 i a v <L 1' u Ia )
Fig. 9 Funciones de Perter.encia FLUJO
Diseño
de
l
a
Base
de
Reglas
Por la forma en cómo se definieron las variables lingüísticas y las funciones que las definen, se cuenta con un total de 5 x 5 = 25
reglas, de las cuales no todas son igual de importantes.
Para este caso se ha considerado necesario el definir las 25 reglas ya que los rangos en los que se le permitirá responder al controlador, incluye los
casos más críticos en los que puede estar el sistema , como ya se ha mencionado, éstos son,cuando eltanque esté vacío y se requiera un punto de ajuste
del 100% o viceversa. Para poder responder bajo estas circustancias críticas, es necesario definir todas las reglas.
 D
D
(..' ¡;
\
¡ e
B l
T !<
º ºR
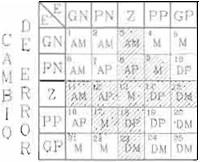
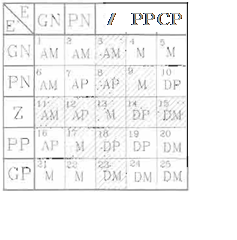
Fig. 1
o
.
Matriz Difusa para el control del Sistema hidraúlico
La matriz Difusa que se muestra en la figura 1O. incluye las 25 reglas que determinan totalmente la respuesta del controlador para cualquier
condición de entradas. Las reglas que están sombreadas, son aquellas más importantes, o bien, las que se utilizan con mayor frecuencia, dado que una
vez que el sistema ha respondido a los casos críticos (reglas de los extremos) su respuesta estará dentro de las 11 reglas consideradas más
importantes.

Procesamiento Difuso y Obtención de la Acción de Control
Como se muestra en la sección anterior, las premisas o condiciones de las reglas, están unidas por un "Y" lógico, es decir, para que una regla se
active, se tienen que cumplir ambas condiciones; a su vez, las 25 reglas se relacionan entre si por medio de un ''O" lógico, esto es, que se puede
activar una u otra regla o bien, otras reglas.
Recordando un poco, se calculan previamente los centroides de las funciones de pertenencia definidas para el Flujo, dado que las funciones consideradas
son simétricas, el cálculo del centrorde se reduce al producto punto entre el vector formado por los cinco centroides y el vector formado por los cinco
grados de pertenencia, entre este mismo vector, como se muestra a continuación :
Donde :
e = rc_DM C_DP C_M C_AP C_AMJ
e = vector de centroides
C_OM = centroide de la función de pertenencia DM
C_DP = centroide de la función de pertenencia DP C_M = centroide de la función de pertenencia M C_AP = centroide de la función de pertenencia AP
C_AM = centroide de la función de pertenencia AM
y el vector formado por los grados de pertenencia de los consecuentes activados por las reglas, GP = lGP_DM GP_DP GP_M GP_AP GP_AM J
donde:
GP = vector formado por los grados de pertenencia activados para cada una de las 5 funciones de salida
GP_DM = Grado de pertenencia de DM (Disminuye Mucho)
GP_::>P = Grado de pertenencia de DP (Disminuye Poco) GP_M = Grado de pertenencia de M (Mantener flujo)
GP_AP = Grado de pertenencia de AP (Aumentar Poco)
GP_AM = Grado de pertenencia de AM (Aumentar Mucho) de modo que el centroide difuso está dado por :
..el
=
C
-
IJM ..GP-
DM - ""
DP*<if' -
DI .:. (-
M <W -
.J ... C-
4 P *(11'-
.-.J> ,_
t AM "' Gf'
AA!
(i)'
_ lJM + GP_ J)P +Gi' _ lvl +úl' _ Al' + GP _ ,-L\/
donde cd = centroide difuso.
En la figura 11 se esquematiza este centroide difuso para una entrada determinada x.
lJi • .'lt- 1 it.1ll '
\I ,p

1 Rl:CLA 1 •>'_1<_1_,1__:... _'_' "_"r,c1.__<'_'_

 C'CN1J?r\1fl[ fllrl :':O
C'CN1J?r\1fl[ fllrl :':O
Fig. 11 Centroíde Difuso

l
,...\.
Como ya se explicó, este valor es único y considera toda la distribución de la salida F, el valor centroide difuso es un número no difuso y es el que
determina la acción de control u que será la variable manipulada que entra al sistema, produciendo una salida y la cual se retroalimentará y se tendrá
otra entrada x para el controlador; este proceso se debe repetir hasta que la salida y sea igual a la entrada deseada, en este caso, hasta que el
sistema se estabilice en el nivel determinado por el punto de ajuste deseado.
RESULTADOS
Tanto el modelo dinámico del sistema hidráulico como el controlador difuso fueron programados en Matlab [19.20). Se analizan 2 casos como ejemplo:
Caso 1: El nivel en el tanque TQ2 es de 60 cm y se requiere un punto de ajuste del 0%, es decir, vaciar el tanque por completo y mantenerlo así. La
figura 12 muestra estas respuestas: la 12.a. presenta la respuesta con Contcolador Difuso, se observa que las reglas que actúan en las primeras 4 o 5
iteraciones son las de los extremos de la Matriz Difusa y luego, las reglas centrales estabilizan al sistema logrando esto en 1O iteraciones.

 .J JA Coit eotrrJIOlftllOR DirUSO
.J JA Coit eotrrJIOlftllOR DirUSO
S• 15 Zll %5
nuafJIM
Fig. 12.a. Controlador Difuso (Punto de ajuste 0%, nivel actual 60 cm)

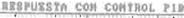
.•Q.
...
:>
s:
ftUUTllU
Fig. 12.b. Controlador PID
Fig. 12. Respuestas con punto de ajuste del 0% y nivel actual 60 cm
La gráfica 12.b muestra la respuesta del PID ante las mismas condiciones de entrada; se ve que responde bastante bien, pero un poco más lento que el
controlador Difuso. ya que éste alcanza el valor deseado por primera vez en 6 iteraciones y el PIO en 10. Al igual que en el caso anterior y
en todos los casos, esto sucedió para unas constantes específicas . También se observa. que el nivel no llega hasta
los o cm, sino que se queda un poco aniba (0.2 cm) y sigue bajando lentamente a lo largo del tiempo.
Si se cambia la constante proporcional , no llega a cero sino hasta después de un gran número de iteraciones.

 Caso 2: Para el caso en el cual los puntos de ajuste sean valores intermedios de puntos que desean aumentar el nivel en el tanque TQ2; como
primer resultado se presenta el obtenido para un punto de ajuste del 6% y un nivel actual de o cm.. éste con la finalidad de ver si los controladores
responden adecuadamente para cambios pequei'los; los resultados se presentan en las figuras 13a y 13b.
Caso 2: Para el caso en el cual los puntos de ajuste sean valores intermedios de puntos que desean aumentar el nivel en el tanque TQ2; como
primer resultado se presenta el obtenido para un punto de ajuste del 6% y un nivel actual de o cm.. éste con la finalidad de ver si los controladores
responden adecuadamente para cambios pequei'los; los resultados se presentan en las figuras 13a y 13b.
r-----.--=•=-&= a:=r,_u,,'=a' t. t cont t ,_oo.;;;....;::..•:'"'"=
us.o , ---
s... ll
::
l
ie
¡
..: . .. .
/
• ltl • 1 • " '" .. .. . -
-• ..
Fig. 13.a. Respuesta con Controlador Difuso
 "f COH ?ROL r r
"f COH ?ROL r r
3
-t :----5;------ 11--- --1S---28 - 2S 38
flUliTlll\S
Fig. 13.b. Respuesta con controlador PID
Fig.1J. Respuestas ante un punto de ajuste del 6% y un nivel actual de Ocm
Como se puede observar. el controlador Difuso se estabíliza en el valor deseado en aproximadamente 5 iteraciones , mientras que el controlador PID lo
logra en casi 1O iteraciones. esto indica que la respuesta del controlador Difuso para los cambios pequeí'los es mucho mejor que la del PID.
CONCLUSIONES
El presente trabajo ha tenido como objetivo el diseñar un controlador por medio de la Lóg1ca Difusa. se diseñó el Controlador Difuso para un sistema
hidraúlico porque se considera que éste es uno de los procesos que más comúnmente se encuentran en la industria. Se dió una introducción a Lógica
Difusa como un método alternativo de control.
Con este trabajo se ha intentado dar una visión general de los conceptos que comprenden a la Lógica Dif usa, desgraciadamente, no se cubre n en su
totalidad los alcances de esta teoría , los cuales van mucho más allá de los expueslos en este trabajo. La teoría,como se ha desarrollado a lo largo d e estas secciones ha sido en su forma más simple, con el objeto de conocer su funcionameinto y factibilidad de aplicación en el control de
procesos. (21-24)
El campo de aplicaciones de la Lógica Difusa es cada día más amplio, y si no se aplica para el control de procesos. se puede aplicar en cualquier
proceso en el que intervenga de manera directa acciones dadas por el pensamiento humano.

R
EFERENCI
AS
1. Zadeh. Lofti A.; Fuzzy Sets and Applications: Selected Papers, John Wiley and Sons lnc., USA, 1987.
2. Johnson, Curtís; Process Control lnstrumentation Technology, Regents/Prentice Hall. lnc.. USA, 1993.
3. Kinney, Thomas; Tuníng Process Controflers, Chemicaf Engineering Magazine. USA, Septiembre,
1983.
4 . Gordon, Lewis; Basic Concepts, Terminology and Techni ques for Process Control, Chemical Engineering Magazine. USA. Mayo, 1983.
5. Tanaka, Masato; Fuzzy Data Smoothíng, Individua! Paper Prepnnt from the ISA ' 92 lnternational Conference and Exhibition. USA, Octubre, 1992.
6. Zimmermann, H.J.; Fuzzy set Theory, Kluwer Academic Publ1shers, USA, 1991.
7. Hohfeld. Markus; Schurmann. Bemd; The Roles of Neural Network s and Fuzzy Logic in Pro cess Optimization, Siemens Review, Alemania , Septiembre, 1993.
8. Pedrycz,Witold; Fuzzy Cont rol and Fuzzy Systems, John W iley and Sons lnc.. USA, 1989.
9. Yamatake, Li-Zheng, Human Operation Emulation Tecflnique Using Fuzzy Contro
.Individual Paper Preprint from the ISA ' 92 lnternational Conference and E.xhib1tion, USA, Octubre 1992.
10. Self, Kevin; Designing wíth Fuzzy Logíc. IEEE Spectrum. USA. Noviembre, 1990.
11. .Terano, Toshiro; Asai, Kiyoji; Sugeno. Michio; Fuzzy Systerns Theory and lts Applications, Academic Press lnc., USA, 1992.
12. Viot. Greg; Fuzzy Loglc in C, Dr. Dobb's Joumal, USA, February , 1993.
13.Kosko, Bart; Neural Networks and Fuzzy Systems. Prentice Hall lnc., USA, 1992.
14.0mron Electronics . lnc; Fuzzy Logic a 21st Century Technology,
Technical lnformation,USA. 1991.
15.Schwarts, Daniel; Klir, George:Fuzzy Logic Flowers in Japan, IEEE Spectrum , USA, Julio, 1992. 16.Cox,
Earl; Fuzzy Fundamentals, IEEE Spectrum, USA, Octubre. 1992.
17. Aranda, Guillermo; Prácticas para el Laboratorio de Control, Manual . ULSA, México. 1993.
18. Rosciano. Antonio. Diseño e Implementación del Laboratorio de Control con un Sistema Hidraúlico, Tesis Profesional, ULSA. México, 1983.
19. Etter, D.M.; Engineering Problem Solving with Matlab. Prentice Hall lnc.. USA. 1993.
20. The Matlab Cuniculum Series; The Student Edition of Mallab for MS-DOS Personal Computers, The Math Works lnc., USA, 1992.
21. Spinrad, Mark;Self-Organizing Fuzzy Control, Individual Paper Preprínt from the ISA ' 92 lntemational Conference and
E.xhibition, USA, Octubre. 1992.
22. Yokogawa Electric Corporation, EF-302 Fuzzy Control Functíon Operation Manual. Japón,
Diciembre, 1992..
23. Yokogawa Electric Corporation. lntroduction to Fuzzy Control, Technical lnformation, Japón. Marzo, 1992.
24. .Youngblood,Rick; Fuzzy Logíc Control of Industrial Processes, Individual Paper Preprint
from the ISA
·91 lntemational Conference and Exhibition. USA. Octubre, 1991.
![]()


 1---1---;
1---1---;
 µA. (x)
µA. (x)
 DEFUZfFlCAClO:'.
DEFUZfFlCAClO:'.
 -
+
-
+



 o 3
o 3

 l.) \ l. (;p
l.) \ l. (;p
 D
D

 .J JA Coit eotrrJIOlftllOR DirUSO
.J JA Coit eotrrJIOlftllOR DirUSO

 Caso 2: Para el caso en el cual los puntos de ajuste sean valores intermedios de puntos que desean aumentar el nivel en el tanque TQ2; como
primer resultado se presenta el obtenido para un punto de ajuste del 6% y un nivel actual de o cm.. éste con la finalidad de ver si los controladores
responden adecuadamente para cambios pequei'los; los resultados se presentan en las figuras 13a y 13b.
Caso 2: Para el caso en el cual los puntos de ajuste sean valores intermedios de puntos que desean aumentar el nivel en el tanque TQ2; como
primer resultado se presenta el obtenido para un punto de ajuste del 6% y un nivel actual de o cm.. éste con la finalidad de ver si los controladores
responden adecuadamente para cambios pequei'los; los resultados se presentan en las figuras 13a y 13b.
 "f COH ?ROL r r
"f COH ?ROL r r