PREDICCIÓN UTILIZANDO REDES NEURONALES Y LÓGICA ABDUCTIVA
Eduardo Gómez Ramirez
y
Rafael Aguilar Agullera
Laboratorio del Centro de Investigación, Universidad la Salle
RESU
MEN
La predicción es una de las áreas en las cuales ha habido un gran desarrollo en los últimos af'ios, principalmente en la predicción de fenómenos de
tipo no línea!, en áreas como: economía, clima. dinámica social, tendencias políticas, etc. Este tipo de sistemas en algunos casos presentan
comportamiento de tipo caótico y su análisis por la cantidad de variables y complejidad de las mismas, requiere de una gran cantidad de herramientas
matemáticas y computacionales complicadas para su observación. En este trabajo se presenta la utilización de varios algoritmos desarrollados
recientemente para predicción: Redes Neuronales (Red Multlcapa y Red Holográfica) y Lógica Abductiva, para la predicción de niveles de contaminación de
la Ciudad de México. También se presentan predicciones para el Indice de precios (S&PSOO).
ASSTRACT
Forecastlng is one of the areas in whlch there has been a great development in the last years, mainly of non-Jlnear phenomenons in areas like: economy,
weather, social dynamic , polltical tendencies, etc. This type of systems in sorne cases have caotlc behavlor and their analysis for the number and
complexity of variables, requires a lot of mathematics and computational tools for their observation. In the current studies the implementation of
severa! algorithms developed recently are introduced for prediction: Neural nets (Multilayer Net and Holographic Net) and Abductive Logic, for the
prediction of pollution levels of Mexico City. Predictions for the stock index are also introduced (S&PSOO).
INTRODUCCIÓN
Hablar del tema de predicción es de gran interés, debido a que los resultados de esta acción son utilizados para tomar importantes decisiones en una
gran cantidad de áreas. Obviamente estas técnicas han tenido gran auge en áreas de tipo económico y político, pero también se han utilizado en el área
médica y biológica.
En el área de predicción de series de tiempo
existen una gran cantidad de herramientas: modelos ARMAX 1 (1), filtro de Kalman (2),y en
los últimos ª"'ºs se han reportado resultados favorables utilizando redes neuronales y lógica abductiva (3,4). Los modelos que se utilizan para la
predicción se pueden clasificar principalmente en dos tipos: los que utilizan los
valores anteriores de la serie (modelo estático) para predecir el siguiente valor y los que

Autoregressive
moving
averge
modef with auxiliary input
utilizan entradas externas que están relacionadas de alguna forma con la salida (modelo dinámico). Para el caso en que se utilizan los valores
anteriores los errores en la predicción dependen de la naturaleza de los datos, por ejemplo si la serie es caótica o no. Este tipo de comportamiento se
ha encontrado en gran cantidad de disciplinas. por ejemplo: astronomía, biología, blofísica, química,
ingeniería, geologia, matemáticas. medicina, meteorologia, economía, ciencias sociales, etc. Este nuevo estado ha pennitido que se distinga
entre sistemas que se pueden denominar ruidosos y sistemas que tienen un comportamiento en "Estado Estableª (5-7). Esta división es importante porque
la aproximación define las herramientas o formalismos que se requieren para su análisis (8-1O), debido a que las técnicas de un sistema ruidoso en
general no son aplicables a un sistema caótico, principalmente si se pretende predecir. Por esta razón, ecuaciones que tienen comportamiento caótico,
son utilizados como estándar ("Benchmark") de prueba para algoritmos de
 95
95
predicción (11). Una de ellas es la serie de Makey-Glass (12), pero existe una gran cantidad de mapeos discretos que también tiene este comportamiento
(13-15).
Para el caso en que se utilizan entradas externas para el modelo, se usan algunas técnicas como la correlación, es decir, si la entrada tiene cierta
correlación con la salida del modelo aunque sea por secciones.
A pesar de lo anterior no existen reglas específicas para obtener resultados favorables, pero sí existen algunas guias que se pueden utilizar. Algunas
de estas guias son que se
nervioso humano está formado aproximadamente por 1012 neuronas y cada neurona está interconectada con 103 neuronas.
La conexión entre cada una de estas neuronas se denomina sinápsis.
Las funciones de estos elementos desde un punto de vista muy simple, son las siguientes:

 o AXON-J
o AXON-J
procesen los datos de entrada (16-18), ya sea
muestreando algunos de ellos u obteniendo la primera diferencia. Esto depende de que es lo que se busca, si se busca el valor exacto o la tendencia de
la serie. También es importante la técnica que se va utilizar para predecir, porque
OENORllAS
_J,
CUERPO
en algunos casos la técnica define el tipo de preprocesamiento.
En este trabajo se hace una breve descripción de dos algoritmos de redes neuronales: red multicapa utilizando regla delta generalizada como algoritmo
de aprendizaje, red neuronal holográfica y por último una técnica no muy difundida: Lógica Abductiva. Se analizan dos ejemplos: en el primero se hace
una comparación en la predicción del nivel de ozono en la zona metropolitana y en el segundo, predicciones del indice S&PSOO (Standard & Poor's
500).
REDES NEURONALES MULTICAPA
Las Redes Neuronales Artificiales (RNA) son modelos matemáticos inspirados en algunas características del Sistema Nervioso. A las RNA también se les
denomina sistemas conexionistas, sistemas adaptables, redes adaptables, neurocomputadoras, procesadores paralelos distribuidos y sistemas neuromóñicos
(19-22).
En la Figura 1 se puede observar una representación muy sencilla de una Neurona Biológica. Esta neurona consiste de un cuerpo denominado soma, varias
ramificaciones del cuerpo conocidas como dendritas y una fibra nerviosa denominada axón. El sistema
Figura 1.Diagrama símplificado de
una neurona bial6g1ca.
las dendritas reciben información de otras neuronas, el soma colecta y combina la información recibida, y el axón envía la información a otras neuronas
(23). El modelo matemático simplificado de una neurona biológica se muestra en la Figura 2. Cada nodo o neurona suma todas las entradas
correspondientes, multiplicando cada una por un coeficiente denominado peso (equivalente a la sinápsis o fuerza sináptica). Esta suma es comparada con
un valor de umbral y si la sumatoria excede el umbral, entonces se produce una salida (equivalente a la
información que envía el axón a otras neuronas o dendritas}. Desde un punto de vista de teofia
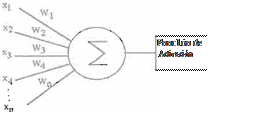
Figura 2. Modelo Matemático simpl ficado de
una neurona
 96
96
de control una neurona puede ser considerada como un sistema de múltiples entradas y una salida (MIS02
A la función que realiza la comparación con el valor de umbral, se le conoce como función de umbral, también se le conoce como
función
En una RNA, el aprendizaje se define como cualquier cambio de los valores de los pesos. Los métodos de Aprendizaje pueden ser clasificados como (20):
• Aprendizaje Supervisado
• Aprendizaje No Supervisado.
de Activación3
También se utilizan otras
funciones como: función sigmoide, tangente hiperbólica, función signo, etc. Estas funciones de activación dependiendo de la "forma"
tienen varias ventajas. Una de ellas es la de limitar la salida correspondiente a un rango definido para
que no sature a otras neuronas. asr como multiplicar por una ganancia a la entrada4 . Las funciones de activación hacen que la respuesta de! nodo sea
de tipo no lineal, y esto permite
configuraciones de varias capas de neuronas.
Una RNA es un conjunto de neuronas ordenadas en alguna estructura específica. A una configuración o estructura en particular se le conoce como
arquitectura . Esta estructura puede ser en forma de capas (Figura 3). Los arreglos en capas también se clasifican según su localización y función
dentro de la arquitectura. La clasificación más común es la siguiente:
• capa de entrada (Input Layer)
• capa de salida (Output Layer)
• capa oculta (Hidden layer)
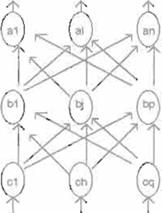
Figura 3. Red
Neuronal Multlcapa

2
MISO
,
multiple-input
-s
íngle-output
3
En la literatura también
se
le conoce como
"Squashing Functíonn o
"
Signa/
Function".
4
El concepto de
ganancia
que se
utiliza es el
mismo
que
en
una función de transferencia.
Las RNA con aprendizaje supervisado como la red de Hopfield o perceptrones son usadas como memoria asociativas o como clasificadores. En el momento del
entrenamiento estas redes "conocen" cuáles son los patrones o·superpatrones" a clasificar dentro de una clase o etiqueta definida. Las redes entrenadas
con aprendizaje no supervisado como el Mapa de Caracterlsticas de Kohonen, son usadas como cuantificadores vectoriales o para fomiar agrupamientos o
clases (clusters). Estas redes no "conocen" la clase correcta en el momento del aprendizaje.
Una de las principales aplicaciones que tienen las RNA son el aproximar funciones, por esta razón y su gran capacidad de representación se les denomina
aproximadores universales (24-29). Por tal razón son utilizadas para aplicaciones como predicción de series de tiempo (30-31), diagnóstico y evaluación
de créditos en bancos, detección de fallas (32-34), identificación de sistemas (35-36), control (37 40), análisis de futuros inventarios en industrias,
análisis de mercados (3,4,41),
planificación y evaluación de proyectos, etc.
Existen reportadas una gran cantidad de algoritmos de RNA aplicados a predicción, pero la arquitectura más utilizada es la multicapa con algoritmo de
aprendizaje retropropagación (backpropagation).
El algoritmo de aprendizaje supervisado que se utilizó en este trabajo, fue Regla Delta Generalizada, y puede ser representado como sigue (42):
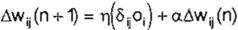 Ec. 1
Ec. 1
donde:
wij es el valor del peso de la i-ésima neurona a la j-ésima neurona.

 97
97

8¡1 corresponde al error de estimación
01 es la salida después de la función de
activación
n es la iteración correspondiente
los valores de et y r¡ son constantes pero pueden varia< dependiendo del error de la red. Normalmente se utilizan a=0.7 y r¡=0.9, pero
algunos trabajos presentan la implementación de redes utilizando lógica borrosa ("fuzzy logíc") para el control de estas constantes. En términos
generales el cambio en los valores de los pesos está relacionado por dos ténninos: el
primero corresponde .a minimizar el error entre
la salida de la red y la salida real, y el segundo término en función del valor del peso anterior. Como se puede observar este es un algoritmo de tipo
gradiente que en la mayoría de los casos converge a un mínimo que no necesariamente es el mfnimo global.
En la siguiente sección se describirá otro algoritmo que se ha utilizado recientemente también para predicción, con una estructura un poco distinta a
la propuesta anterionnente.
iterativo como el caso de la RDG. La respuesta genera un grado de libertad (magnitud del vector de respuesta) , asf como una componente asociada de
información analógica (ángulo de fase).
Otra característica importante del método holográfico es que no existe una limitación en el número de patrones como sucede por ejemplo con el Modelo de
Memoria Asociativa Bidireccional y en el Modelo de Hopfield.
Preprocesamiento
La RNH trabaja con números complejos (representación de magnitud y fase), por lo cual se requiere convertir números reales a una representación
interna. Esto se realiza por una operación de preparación o preprocesamiento de la información llamada "preprocesamiento sigmoidal" {43-45).
Este procedimiento es un mapeo de un escalar a un complejo tal que:
REDES NEURONALES HOLOGRAFICAS
(RNH)
El término "holográfico" es utilizado por la similitud de este esquema con las matemáticas desarrolladas en la teorfa del campo electromagnético y almacenamiento de
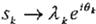 donde :
donde :
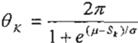 Ec. 2
Ec. 2
información observado en los hologramas ópticos.
El método holográfico tiene una característica distinta de otros paradigmas neuronales que se le asemejan en operación: este método tiene la habilidad
de sobreponer múltiples asociaciones (patrones) de estímulo respuesta (mapeo) en la misma cadena de correlación. Esto se obtiene, realizando la
diferencia de fase de cada punto con respecto a todos los demás puntos involucrados en el patrón (cada punto almacena el patrón desde su muy particular
punto de vista).
Las asociaciones individuales (patrones) son codificadas o aprendidas de una forma determinística durante un proceso que no es

5 Diferencia entre Ja salida real y salida de ta red

 98
98
sk es el k-ésimo término de la serie de tiempo
µ es la media sobre la distribución del vector de entrada
o es la desviación estándar sobre la distribución del vector de entrada
Codificación (Aprendizaje)
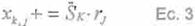 Para la etapa de codificación o aprendizaje el método genera una matriz de memoria. Este procedimiento es análogo a la Regla de Hebb utilizada para
obtener la matriz de memoria del modelo de Hofpield. La matriz puede ser obtenida como:
Para la etapa de codificación o aprendizaje el método genera una matriz de memoria. Este procedimiento es análogo a la Regla de Hebb utilizada para
obtener la matriz de memoria del modelo de Hofpield. La matriz puede ser obtenida como:

El proceso de codificación (aprendizaje) para múltiples patrones puede ser representado de por la siguiente fórmula:
[X] += [S]T [R] Ec. 4
donde :
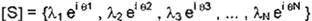
es el vector de entrada (o estímulo) del modelo holográfico
[R] - {11 et 1 , Y2 e192 , y3 el +J , ... . YN e1+N }
es el vector de salida (o respuesta) que se desea obtener utilizando el estimulo S. Evaluando la expresión obtendrfamos:

 p
p
razonamientos bajo ciertas Incertidumbres. La incertidumbre se presenta cuando existe insuficiente Información para obtener conclusiones con absoluta
certeza. Esto es causado por niveles de ruido en el sistema, posibles truncamientos numéricos, insuficientes
datos o variables, etc.. La estructura de LA es semejante a la de RNA, pero la estructura se clasifica principalmente en los siguientes tipos de nodos
(47}:
1.- Sencillo:
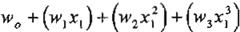
2.- Doble
w
0
+(w1x1)+(w2 x2 )+(w3x:) +(w4 x;)
'""'
A.
r
e'(;,-8,_,)
+(w
x x
)
+(w
x;)
+(w1x:)
.(_¡
l
,
l
1,1
l
[
X ]
=
"L'°.'.2 y e'<;,.-81,>
5 1 2
6
p
2,t 2,t Ec. 5
3.- Triple
w
+ (w x ) + (w
x ) + (w x ) + (w4 x?)
Decodificación
(Generación de Salida}
En esta parte la RNH genera una respuesta utilizando la nueva entrada . Los elementos de generación de salida son una vez más complejos. La decodifica
ción es la siguiente:
[R] =.!.[sr .[ x] Ec. s
e
donde [Sr es el nuevo estímulo. Este nuevo estímulo de entrada puede ser representado por:
[S]* = {/..* 1 e' a·1 A.•2 e' e'2 , A....3 e¡e-J , ... ,'Al *N e1
+{wxi)+(w6 x:)+ (w1x1x2 ) +(w8 x1x3)
+(w9X2 X3) +(w,0X1X2 X 3) +(w1,x;)
+(w12xi) +(w13x:)
4 .-
Elementos Blancos (Whlte Elements). Estos elementos son la combinación lineal de las variables de salida de la capa anterior
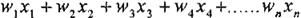
5.- Normalizadores: Este elemento modifica la media y varianza de la señal de entrada
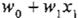
6.- Unificador: Este elemento es el mismo
LÓGICA ABOUCTIVA (LA)
e·N }
pero con la diferencia que es utilizado para ajustar la señal de salida al valor de la red.
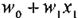 El término Abducción fue utilizado a finales de 1800 principalmente por el Filósofo Charles S. Peirce. Este término ha sido utilizado en varios
sentidos, pero el principal es el hacer
El término Abducción fue utilizado a finales de 1800 principalmente por el Filósofo Charles S. Peirce. Este término ha sido utilizado en varios
sentidos, pero el principal es el hacer
Como se puede observar esta red utiliza los últimos resultados que se tienen en preprocesamiento de los datos en RNA y los que se han encontrado para
la optimización de
 9
9
9
9

la arquitectura de redes neuronales en función del error de predicción. La red encuentra la arquitectura más optima en función de los nodos descritos
anteriormente (48).
PREDICCIÓN DE LOS NIVELES DE
CONTAMINACIÓN EN LA CIUDAD DE
MÉXICO
.
En esta sección se presenta la implementación de los algoritmos anteriormente mencionados, para la predicción del indice Metropolitano de Calidad del
Aire en la Cd. de México (IMECA).
Descripción Ejemplo.
En este caso se utilizarán CQmo entradas las siguientes variables climatológicas:
• Velocidad del viento
• Nivel de lluvia
• Visibilidad
• Presión
• Nubosidad
• Insolación
• Temperatura
Estos datos fueron tomados por día de los registros del Observatorio Nacional. Para la salida se tomó el índice promedio de Ozono (48-49) por día que
se encontraba en el aire de la zona correspondiente al Observatorio. Para el experimento se utilizaron los meses de
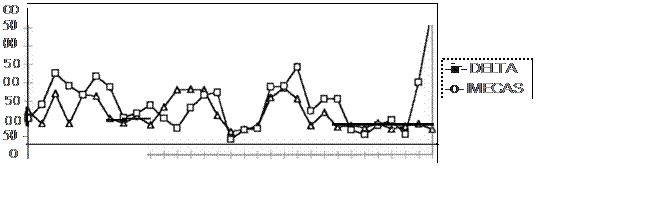
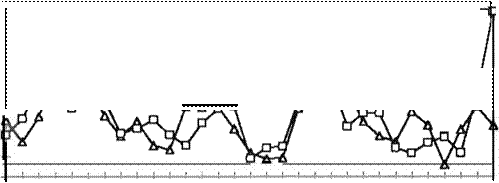
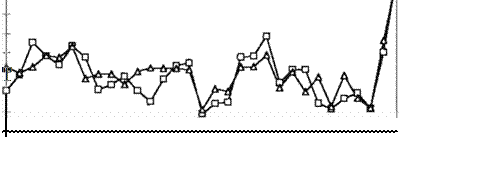
noviembre y diciembre de 1991 (50) CQmo archivos de aprendizaje y el mes de enero de 1992 se utilizó como prueba de la red. En la Figura 4 se pueden
observar las diferentes
predicciones utilizando las técnicas descritas en las secciones anteriores. En la Tabla 1 se presentan las correlaciones entre el valor real y las
distintas predicciones .
|
IMECAS/RDG
|
IMECAS/RNH
|
IMECAS/LA
|
|
0.5251
|
0.6192
|
|
0.858303
|
|
|
Tabla
1
.
Correlaciones de las predicciones
con el indice metropolitano de calidad
de!
aire
(IMECAS).
T
abla 2.Correlación de las Salidas
Estimadas
y
el S&PSOO
|

S&P500/LA
|
S&P500/RDG
|
S&PSOO/RNH
|
|
0.99257
|
|
0.8854
|
0.874143
|
|
|
|
|
|
PREDICCIÓN
S&P500
Para este ejemplo se utilizó un Indice de precios bastante utilizado: S&P500. Los datos se tomaron de un ejemplo de predicción de un capítulo de un
libro, que analizaba el comportamiento del algoritmo backpropagation (51). En este ejemplo se analizaron 200 semanas para el archivo de entrenamiento
del período de enero de 1980 a octubre de 1983. Se utilizaron 27 entradas tales como: el valor del índice más alto y más bajo de esa semana y otros
indices como NYSE (New Yorl< Stock Exchange). se utilizaron SO semanas posteriores para prueba de predicción. Los Resultados se pueden observar en
la Figura 5.
En la Tabla 2 se muestran las correlaciones de índice y sus estimados por medio de RDG, RNH y LA.
Como se puede observar para los dos ejemplos los mejores resultados se obtuvieron con lógica abductiva que utilizando técnicas de redes neuronales.
CONCL
USIONES
Los diferentes paradigmas de redes neuronales han demostrado su gran capacidad de representación de información, así como su capacidad de extraer
características que no pueden ser representadas por técnicas
estadísticas clásicas. En este trabajo se
presentó de forma muy breve la aplicación de modelos holográficos neuronales, modelos multicapa y lógica abductiva en el área de predicción. Es
Importante destacar que las redes neuronales sin importar qué paradigma se esté utilizando, no son la "panacea" a todos los problemas de predicción, en
muchos casos se obtienen mejores resultados cuando se combinan diferentes técnicas tanto para el
 100
100
procesamiento de los datos de entrada, como variaciones internas del modelo que son utilizadas en otros paradigmas. Una de las
ventajas que tiene LA es que su algoritmo utiliza varias de las aportaciones de los últimos resultados en predicción sobre el
PREDICCIÓN IMECAS ENERO 94
 4
4
3
3
00
2
u 2
- 1
1
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
 400
400
350
 V.l 300 250 200 150 - -
V.l 300 250 200 150 - -

100
50
o
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31

1so
100
50
o
 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
DIAS
Figura 4. Predicción delos niveles de contaminaciónonla ciudad de México
 101
101

preprocesamiento de los datos. Un trabajo futuro sería combinar todas estas técnicas con las ventajas y desventajas de cada una y hacer
una vez más las comparaciones anteriores.
AGRADECIMI ENTOS
Se agradece la colaboración del personal del Observatorio Nacional por las facilidades otorgadas para la adquisición de los datos meteorológicos. A la
maestra Esther Va rgas por sus comentarios y sugerencias en los experimentos y al grupo de Redes Neuronales del Laboratorio del Centro de Investigación
por su apoyo en el procesamiento de los datos y experimentos.
REF
E
ENCIAS
1. Box G. & Jenkins G. Time Series Ana/ysis Forecasting and Control. Holden-Day Series in Time Series
Analysis. 1970.
2. Gardner W. lntroduction to Random Processes with Applications to Signals a nd Sysfems. MacGraw Hill. 1990.
3. Kean, J. Chaos Theory and Neural Networl< Analysis. Technical Analysis of stocks & Commoditíes,
June. 1992.
4.
Fishman. M; Barr, D. & Loick, W. Using Neural Nets in Market Analysis. Technica/ Analysis of Stocks & Commodities. April. 1991.
S. Bak P. & Chen K. Se/f Organized Cliticabi/ity. Scientific American. January. 1991.
6. Dubois M., Aften P. & Bergé P. "El orden Caótico". Mundo Cientffico. Vol. 7 No. 68. 1986.
7. Peters, E. Chaos and Order in the Capital Markets. John Wiley & Sons. lnc. 1991.
8. Angeles, F; Sepulveda, D. & González, H. Simulador de Sistemas No lineales enfocado al fenómeno de caos. .XXXV Congreso Nacional de Flsíca. 26 al 30 de octubre, Tonantzintla, Puebla, México.
1992.
9. Angeles-Femández, J. C., González Hemández. H. SIMCAOS: A Nonlinear Dynamics simulator. Fírst Jntematíon al Conference on Dynamic System and Applications, Atlanta GA U.S.A. May, 1993.
10. Chua L. & Parker T.: Chaos: A tutorial for Engineers, Proceedings of the IEEE. Agosto Vol. 75 No. 8. 1987.
11. Chakraborty K., Mehrotra K, Mohan K & Ranka S. "Forecasting the Behavior of Multivariate Time Series Using neural Networks". Neural Networks. Vol. 5. 1992: 961-970.
12. Mead W., Jones R., Lee Y., Barnes C, Flake G., Lee L., & O'Rourke M. ªUsing CNLS-Net to Predict the Makey-Glass Chaotic Time Series".CNLS NewsJetter, Center for nonlinear Studies Los A/amos National Lab., No. 69 August 1991.
13. Farmer J. & Sidorowich J. "Predicting Chaotic Time Series". Physica/ Review Letters. Vol. 59 No.
8. 1987.
14. Stark J. "Recursive Prediction of Chaotic Time Series". Joumal of Nonlinear Science. Vol. 3.
1993:197-223.
15. May R. "Simple Mathematical models with very complicated dynamics•. Nature. Vol. 261. June. 1976.
16. Crooks T. "Care and Feeding of Neural Networks". AJ Expert. Julio 1992.
17. Lawrence J. "Data Preparation for a Neural Network". Al Expert. Noviembre 1991.
18. stein R. "Preprocessing Data for Neural Networks". Al Expert. March. 1993.
19. Simpson P. Artificial Neura/ Systems, Foundations, Paradigms, Applicafions , and lmplementations. Pergamon Press. 1990.
20. Lippman R., "An lntroduction to Computign with Neural Nets. IEEE ASSP Magazine. Abril 1987.
21. . Alexander. l. "lntroduction to neuraf nets".
Chapter 9 in "Applied Artificial lntellígence·,
 102
102
ed. K. Warwick, Peter Peregrinus Ud.,
1991.
22. Caudill M. & Butler Ch. Understanding Neuraf Networ1<s. Vofume 2: Advanced Networks. MIT Press, 1994.
23. Stevens F. "The Neuron". Scientific American . 1979.
24. Cotter N. "The Stone-Weierstrass Theorem and lts Application to Neural Networks". IEEE Transactions on Neural Networ1<s. Vol.
1, no. 4. Diciembre 1990:290-295.
25. Girosi F. & Poggio T. "Networks and the Best Approxlmation Property". Biologicaf Cyberneocs. 1990.
26. Homik K., Stinchcombe M. & White H. "Multilayer Feedforward Networks Are Universal Approximators". Neural Networks. 1989.
27. Cybenko G. "Approximationn by Superpositions of Sigmoidal Function". Mathematics of Control Signals and System. Vol. 2. 1989:303-314.
28. Rao D. & Gupta M. "Dynamic Neura! Units and Function Approximation". IEEE Conference on Neura/ Networ1<s. 28 de Marzo a 1de Abril de 1993.
29. Funahashi K. "On the Approximate Realization of Continuous Mappings by Neural Networks". Neuraf Networ1<s. vol. 2, 1989:283-192.
30. Werbos P. The Roots of Backpropagation, From order derivatives to Neural Networl<s and Political Forecastíng. Wíley lnterscience. 1994.
31. Rogers D. Weather Prediction using a Genetic Memory. Neural Networks. Concepts, Applications, and lmplementations. Volume IV. Paolo Antognetti
& Eljko Milutinovic Editors. Prentice Hall. 1991.
32. Hoskins J., Kaliyur K. & Himmelblau D. "Fault Diagnosis in Complex Chemical Plants Using Artificial Neural Networks". AIChE Joumal.
vol. 7 No. 1. Enero 1991.
33. Priddy K., Lothers M. & Saeks R. Neural Networks and Fault Diagnosis in Rotating Machinery. Proceedings of IEEE lntemationaf Conference on System Man and Cybernetics 1993.
34. Salchenberger M., Cinar E. & Lash N. Neural Nefworl<s: A new Tool for Predicting Thrift Failures. Decision Sciences, vol. 23. 1992.
35. Riedmiller M.·controlling an lnverted Pendulum by Neural Plant ldentiflcation•. Proceedings of IEEE fntematíonal Conterence on System Man and Cybernetics 1993.
36. Sadegh N. "A Perceptron Networ"K for Functional ldentiflcation and Control of Nonlinear Systerns". IEEE Transactíons on Neural Networl<s, Vol. 4 No. 6. November, 1993:982-988 .
37. Bhat N. & T. J . Mc-Avoy. "Use of Neural Nets for Dynamic Modeling and Control of Chemical Process Systerns". Computers Chem.Eng., No.14, 1990:573-583.
38. Buttazzo G., Allota B., & Fanizza F. Mousebuster. "A Robot for Real-Time Catching". Control Systems. Vol. 14 No. 1, February 1994.
39. Gupta M. & Rao D. "Neuro-Control Systems: A Tutorial". Neuro-Control Systems, Theory and Applications. IEEE Press.1994.
40. Narendra K. s. and K. Parthasarathy. "ldentífication and Control of Dynamical Systems Using Neural Networks". IEEE Trans. Neural Networ1<s, No.1. 1990:4-27.
41. Kimoto T. & Asakawa K. "Stock Market Prediction System with Modular Neural Networks". lnternational Conterence of Neural Networl<s. 1990.
42. Pao, Y. Adaptfve Pattem Recognffion and neural networ1<s. Addison Wesley Publishing Company, lnc. 1989.
43. Soucek, B. Fuzzy, Holographíc, and Para/le/ lnte//ígence. Wiley-lnterscience. 1992.
 ;====================================:======::::=::===· 103
;====================================:======::::=::===· 103
44. Sutherland, J. A Ho/ographic Model of Memory, Leaming and Expression. 1nternational Journal of Neural Systems.
1990.
45. suthertand, J. The Ho/ographíc Ce// -A
Quantum
M
odel.
AND Amenca Ud.
46. . AIM, The Abductive lnfomiation Modeler. User's Manual. AbTech Corporation . 1995.
47. Gómez E. & Poznyak A. How to Select a Numbers of Nodes in Artificial Neural Networl<s. CAM 94. Cancún México. Septiembre 26-30 . 1994.
48. Bravo, H.; Roy, G.; Sánchez, A. & Torres, J.·contaminación atmosférica por ozono en la zona metropolitana de la ciudad de
México: Evolución Histórica y Perspectivas". OMNIA. Año 7 número 23, junio, 1991.
49. Bolat'los, F. "Dimensiones del problema ambiental contemporáneo·. OMNIA. Año 7 número 23, junio, 1991.
50. Gómez E., Pérez G. & Polanco M. "Forecasting of the Pollution Levels in Me.xico City using a
Neural Network". IEEE Systems, Man and Cybemetics '93 Conference. Le
Touquet-France, October 17-20, 1993.
51. Welstead Stephem. Neural Network and fuzzy logic applications in C/C++. Wiley. 1994.
![]()
![]() 95
95

 o AXON-J
o AXON-J






 4
4
 400
400
 V.l 300 250 200 150 - -
V.l 300 250 200 150 - -

 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31

 ;====================================:======::::=::===· 103
;====================================:======::::=::===· 103