DESCRIPTORES DE SENALES CAÓTICAS
Ma. Carmen Lu
l
e-Carpinteyro, Pedro
c
.
Estrada Gutiérrez
y
H
ugo G. González Hemández
Laboratorio del Centro de Investigación, Universidad
La
Salle
RESUMEN
En el presente trabajo se muestra un programa especializado para la descripción de la caoticidad tanto de un sistema de ecuaciones diferenciales o en
diferencias como para una serie de tiempo. Uno de los problemas en el estudio de caos es la falta de herramientas accesibles para describir en forma analftica las características del sistema caótico. A estas herramientas las hemos llamado descriptores de la señal caótica. Los descriptores
que se presentan en este trabajo son fundamental mente dos: Exponentes de Lyapunov y Dimensión Fractal, ambos Implementados para los casos mencionados
al principio de este resumen. Se presentan diferentes ejemplos y se comparan contra mapas de bifurcaciones obtenidos en nuestro laboratorio. Para
series de tiempo se presentan estos descriptores aplicados a diferentes tipos de ruido.
ABSTRACT
This paper shows a speclalized program for chaotic level description of dynamic systems and time series. A problem with chaos study is the lack of
flexible tools to describe analytically the chaotic system properties. These tools have been called Chaotic Signa! Descriptors. Descriptors presented
in this paper are: Lyapunov exponents and Fractal dimension, both able to apply upon dynamic systems and time series. Severa! examples are presented
and compared with bifurcation maps obtained in our laboratory. For time series, descriptors are applied upon severa! kinds of noíse.
I
NTRODUCCIÓN
Una evidencia convincente para detectar y cuantificar el caos determinístico en sistemas no lineales puede encontrarse al emplear diferentes
herramientas. Nosotros nos hemos enfocado principalmente en dos de ellas: el espectro de los exponentes de Lyapunov y en la dimensión del sistema, para
lo cual nos hemos basado en programas existentes en nuestro laboratorio. Se abarcan tanto sistemas discretos no lineales, como series de tiempo, cuyos
problemas serán tratados a lo largo del articulo.
EXPONENTES
DE LYAPUNOV
Los exponentes de Lyapunov son el promedio de rangos exponenciales de divergencia o
convergencia de las órbitas adyacentes en el
corresponden a estados cercanos Idénticos , cuando órbitas exponenciales divergen significa que el sistema pierde rápidamente su habilidad o propiedad
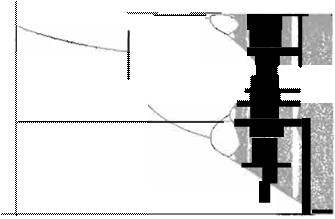
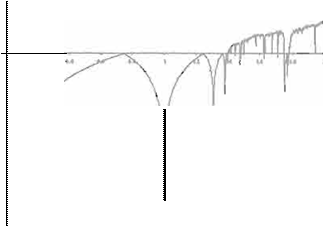
de predicción (Figura 1).
Un sistema dinámico disipativo con al menos un exponente negativo, hará que la suma sea negativa, indicando que el movimiento post-transitorio de
trayectorias ocurrirá sobre un volumen cero del conjunto límite, así mismo un sistema con al menos un
exponente de Lyapunov positivo es considerado como caótico2, siendo la magnitud
del exponente la que refleja la escala de tiempo en la que el sistema dinámico empieza a ser impredecible.
Para sistemas en los cuales se conocen sus ecuaciones de movimiento es posible calcular todo el espectro de los exponentes de
espacio de fase1
Estas órbitas adyacentes
2 Pues el exponente positivo refleja una "dirección" en la cual el sistema experimenta
1
Es
decir,
que Ja
suma de los exponentes es
el tiempo
promedio de divergencia
de
la
velocidad en
et espacio de
fase.
un proceso
repeütivo
de contracción
y
desdoblamiento
que decorrelacíonan estados
adyacentes en
el atractor.
'
1
09
...
..,.
.... ...
....
.....
......
......
....
...
Fi
gura 1. Mapa
de
bifurcación
y
Espectro de Lyapunov
Lyapunov, no siendo así para datos experimentales pues contienen ruido externo que provoca fluctuaciones y limitan 18 resolución experimental. Sabemos
que estos datos experimentales son observaciones derivadas del sistema. Existen técnicas de reconstrucción del espacio de fase con coordenadas
retrasadas que hacen posible obtener mediante una serie de tiempo un atractor cuyo espectro de Lyapunov es idéntico al del atractor original. El
exponente de Lyapunov se puede definir de la siguiente forma:
1
11
-
1
il
= lim-¿tnl f'( x(i)J I (1)
n
-+
<0
n
l
r=
O
donde A. es el exponente de Lyapunov y f'(x(i)) es la derivada de la trayectoria para el i-ésimo punto. La estimación de los exponentes de Lyapunov
para una serie de datos experimentales es un poco diferente a la determinación de éstos a partir del modelo matemático. Consideremos el caso más
simple: la determinación del exponente más grande. Comenzamos escogiendo una "trayectoria auxiliar" y una "trayectoria de prueba". Se desea evaluar la
razón local de divergencia entre las dos trayectorias promediadas a lo largo del atractor. Se escogen dos puntos iniciales lo más cercano posible uno
del otro, pero cuya separación temporal en la serie de tiempo es no menor que un periodo promedio de la órbita.
Cuando se trabaja con series de tiempo el número de datos experimentales es limitado y algunas veces se pueden tener errores, principalmente por que la
distancia mínima
disponible es demasiado larga . Para cualquier clase de atractor dado, la claridad depende de la calidad y la cantidad de los datos experimentales.
DIMENSIÓN
La dimensión es utilizada para poder caracterizar las propiedades de un atractor. Generalmente, la dimensión puede ser definida como la información
necesaria para especificar la posición de un punto sobre el atractor dentro de los límites de una ocurrencia dada, o también como el nivel más bajo del
número de variables esenciales necesarias para modelar la dinámica del sistema. Para atractores simples, definir y determinar la dimensión es fácil,
por ejemplo, usando cualquier definición razonable de dimensión, un tiempo de equilibrio independiente estacionario (punto fijo) tiene dimensión cero;
una oscilación periódica estable (ciclo límite) tiene dimensión uno y un atractor de doble periodo (toroide) tiene dimensión dos. Esto es, porque su
estructura es muy regular de tal manera que la dimensión de estos atractores tienen valores enteros .
Los atractores caóticos, sin embargo, la mayor parte de las veces tienen una estructura no tan simple (frecuentemente tiene estructura múltiple), por
lo que su dimensión tiene valores no enteros. Para entender las propiedades de un atractor caótico. se debe tomar en cuenta no solo el atractor en sf
mismo, sino también la "densidad" de los puntos sobre el atractor.
Como en el caso de los exponentes de Lyapunov, el cálculo analftico de la dimensión
fractal se restringe a un número pequeño de casos. La dimensión fractal es definida a
continuación. Sea s un conjunto de puntos en
un espacio euclidiano. Considere ciertos hipercubos de lado e y calcule el número mínimo de tales celdas N(s) necesarias para cubrir S. Es decir:
Para sistemas experimentales, sin embargo. cuando se dispone en la serie de tiempo de una sola o pocas varlables, la situación es más dificil. En la
práctica primero que nada se supone la dimensión del atractor del sistema que ha generado los datos experimentales. Entonces uno trata de acomodar la
serie de tiempo en esa dimensión y trata de reconstruir
ese atractor y estimar su dimensión de
D
= lim log(N(e))
c-+O
/og(l
/ E)
(2)
correlación. Este proceso es Iterativo para dimensiones mayores. En un principio, mientras la dimensión supuesta del atractor Ds
no puede ser calculada en una forma sencilla y no se garantiza la convergencia del limite. Grassberger y Procaccia (1983) sugieren una aproximación
diferente . La idea básica es la de reemplazar el clásico algoritmo de conteo de cajas con la medida de las distancias entre puntos que representen
posiciones del sistema a lo largo de una órbita del atractor. Suponga que se empieza a partir del sistema de ecuaciones diferenciales:
x
=
f
(x
),
x
E W
Por integración numérica obtenemos una trayectoria que consiste en N puntos discretos
{x, }:,= {x( t + i-z)} , , donde 't es un inteNalo de tiempo arbitrariamente fijo, y los puntos iniciales han sido
seleccionados para descartar los transitorios . Definimos la función de correlaclón
j
N
C(r)
=
lim
2
'L,
U(r
-
l
x
1
-
x
.
I
J
N -+oo J
l
,
j•/
es menor que la del atractor real D,. Ds continuará aumentando. Si el sistema es determinista, Ds converge a D,. En el caso opuesto de que el sistema
sea puramente aleatorio De tenderá a infinito.
CONCL
USI
ONES
En general es complicado analizar sistemas caóticos. Se complica más cuando se tiene un sistema experimental, esto es, una serie de datos de los cuales
se quiere averiguar su caoticidad ya sea para controlarlo, aprovecharlo o simplemente analizarlo. Este trabajo considera dos medidas de la caoticidad
de un sistema en general. ya sea en forma de serie de tiempo o en forma de ecuación dinámica. En nuestro laboratorio se tienen los programas que
obtienen estos dos descriptores. Se están desarrollando programas para obtener otros descriptores.
REFERENCIAS
(3)
para í;tj, donde U es la función de Heavyside o escalón unitario. Para r·s pequeñas, C(r) se comporta como una potencia de r. Entonces,
(3) se puede escribir como:
C
(r)
-;::.
rº'
(4)
donde De se llama la dimensión de correlación. En estimados numéricos, en donde el número de puntos es ilimitado y la precisión es finita, para r
demasiado pequeñas las estadísticas estimadas son pobres, ya que el número de obseNaciones es pequeño y los errores pueden ser grandes.
1. Parker, T. S., Chua, L. o. Chaos: A Tutorial Far Engineers. Proceedíngs of fhe IEEE. 1987.
2. Medio, A., Gallo, G. Chaotics Dynamics. Theory And Applications To Economics. Cambridge
University Press. 1992
3. Wolf, A., SWift, J., Swinney, B.. Vastano,
H. L. Determining Lyapunov exponents from a time series. Physica 160, 1985:285- 317.
4. Farmer, J. D., Edward, O., Yorke . J . A The Dimenslon Of Chaotic Attractors. Physica 70, 1983:153-180.