 SOLUCIÓN DEL PROBLEMA DE LA CINEMATICA INVERSA EN ROBÓTICA UTILIZANDO LÓGICA DIFUSA
SOLUCIÓN DEL PROBLEMA DE LA CINEMATICA INVERSA EN ROBÓTICA UTILIZANDO LÓGICA DIFUSA
Alejandro Eguiarte Salazar y Eduardo Gómez Ramírez Laboratorio delCentro deInvestigación, Universidad La Salle
RESUMEN
En algunos casos es de gran dificultad et encontrar una solución al problema de la cinemática Inversa en robótica debido a las no-linealidades de su
ecuación. Investigadores en todo el mundo han desarrollado diferentes alternativas para encontrar la solución óptima a este problema. Los últimos
resultados reportados muestran el uso de Redes Neuronales Artificiales, Algoritmo Genético y Lógica Difusa para la solución de este problema. En este
trabajo se presenta el diseno de un controlador utilizando lógica difusa para resolver el problema de la Cinemática Inversa, considerando únicamente la
manera en que, inconscientemente, usamos nuestro brazo, antebrazo y muneca para alcanzar algún objeto.
ABSTRACT
Flnding a solution to the lnverse Kinematics Problem (IKP) in Robotics Is, sometlmes a challenge difficult to race because of the inherent
nonlinearities of its equatlons. Researchers of ali the world have developed ways to find the optima! solution to this problem. Latest reports show the
use of neural networ1cs, genetic algorithms and fuzzy logic (to name a few). for the solution of this problem. In this paper we designed a Fuzzy Logic
Controller to solve the IKP, considering only the logical manner we unconsciously use to move our upper arms, forearms and wrists to reach things.
INTRODUCCIÓN
En la actualidad existe un creciente Interés en la investigación y desarrollo de controladores que utlllzan técnicas de inteligencia artlflclal para la
determinación de sus diferentes salidas de control. La razón principal es por la versatilidad y confiabilidad que estos controladores pueden
llegar a tener. Una de las técnicas utilizadas es la Lógica Difusa (LD). Algunas de las aplicaciones prácticas de la LD que existen en la actualidad
son (1): controladores para el mecanismo de
autoenfoque en cámaras de 8mm, frenos antibloqueo, sistemas de transmisión automática, controles de temperatura, humedad o nivel, etc.
Una de las razones principales del uso de la LD es que el algoritmo por naturaleza, permite procesar información de forma semejante al cerebro humano
(2). Esta característica, desde el punto de vista de teoría de control, tiene vanas ventajas: la primera y principal es que no se requiere del modelo
matemático del sistema
a controlar. La segunda es que el diseño del control es simple, es decir, se requiere de menores herramientas ·matemáticas para el diseño de un
controlador que por técnicas clásicas (3). Esta caracterfstlca es Importante debido a que diseñar un controlador que sea robusto y adaptable
puede llegar a ser muy complejo. Una ventaja más que tienen los controladores difusos consiste en que es posible conocer exactamente su
funcionamiento interno ya que la acción que ha de realizar el sistema difuso se encuentra descrita por un conjunto de reglas de inferencia, de manera
que puede determinarse el estado del sistema en cada instante.
Uno de los problemas en Robótica en los cuales se ha utilizado LD y otra técnica llamada Redes Neuronales Artificiales (RNA). es el de la cinemática
inversa de un manipulador. En este trabajo se presenta una alternativa a la solución de este problema utilizando LD, considerando la forma natural en
que un humano toma un objeto. El artículo está estructurado de la siguiente forma: En la
 2 17
2 17

primera parte se describe brevemente el problema de la cinemática directa e inversa utilizando técnicas tradicionales; en la segunda sección se definen
las variables y tune.iones que se van utilizar para el control del manipulador, as!como las reglas de inferencia. En la tercera sección se presentan
algunas simulaciones para un manipulador de tres grados de libertad, y por último presentamos
las conclusiones y perspectivas.
EL PROBLEMA OE LA CINEMÁTICA
DIRECTA
La poslción de un manipulador o brazo de robot puede expresarse de dos formas: utilizando coordenadas cartesianas o bien coordenadas articulares. Las
coordenadas cartesianas se
establecen con respecto a los ejes coordenados mientras que las coordenadas articulares consideran cada articulaclón como un eje coordenado . En la
práctica las consignas útiles
para los dispositivos actuadores suelen ser consignas de posición en el espacio de coordenadas articulares. Por lo tanto, se requiere encontrar una
transformación de un sistema de coordenadas a otro para relacionar
estos dos espacios. Sea la transformac ión:
X
=
f (q)
Ec.1 donde x es un vector que representa la posición
y orientación del órgano terminal en el espacio
de coordenadas cartesianas, y q es un vector de posiciones articulares . La ecuación 1 es la formulación del problema de Cinemática Directa en et cual dadas las posiciones
articulares q, se calcula la posición y orientación del órgano terminal del manipulador
x
en el espacio de coordenadas cartesianas. Es
decir, el objetivo de la Cinemática Directa consiste en determinar el efecto total acumulado dado por las variables de unión. en este caso los ángulos
de todos y cada uno de los eslabones. El problema de la Cinemática Directa tiene una solución simple. El procedimiento consiste en comenzar en
la base de soporte del manipulador y sucesivamente calcular la posición y orientación de cada eslabón para determinar la posición y orientación del
órgano terminal. En este procedimiento, a menudo se usan transformaciones homogéneas para especificar
la posición y orientación de cada eslabón con
respecto a un sistema de coordenadas de referencia.
EL PROBLEMA DE LA CINEMÁTICA
I
NVERSA
El problema inverso al de la Cinemática Directa podemos definirlo como la función Inversa de la ecuación 2 definida como:
q
= g(x) = f -l(x) Ec. 2
la cual es la formulación del problema de ta Cinemática Inversa, en el cual, dada la posición y orientación del órgano terminal o efector x,
en
el espacio de coordenadas cartesianas, se calculan las posiciones articulares q del manipulador.
El problema de la cinemática Inversa no es tan simple como el anterior, y como se sabe no existe una solución única para resolver este problema. Para
simplificar esta solución, en el diseño de la mayoña de los manipuladores se toman en cuenta ciertos criterios como que los ejes de movimiento
articular vecinos sean ortogonales o paralelos unos con otros, o bien que tas primeras tres articulaciones sean las encargadas del posicionamiento
espacial del órgano terminal, dejando que las tres últimas articulaciones formen una mui'\eca esférica, la cual será la encargada de la orientación del
órgano terminal.
La solución de la Cinemática Inversa para el manipulador de 3 eslabones (3) puede obtenerse realizando una aproximación geométrica al problema,
suponiendo un valor determinado para el ángulo j3 y calculando los otros dos de acuerdo a las siguientes ecuaciones que parten de la aplicación de la
Ley de los Cosenos y otras consideraciones geométricas:
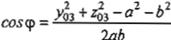 Ec. 3
Ec. 3
donde y03 y 1-03 son las coordenadas del origen del último sistema de coordenadas para el eslabón que contiene al efector.
Transformando la ecuación anterior para poder obtener las dos soluciones se tiene que:
 218
218

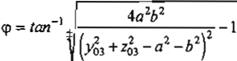
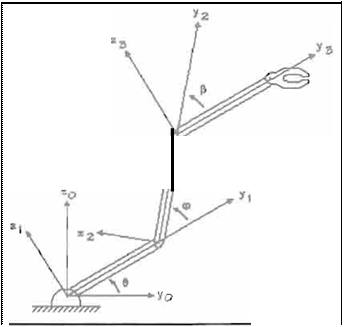 Ec. 4
Ec. 4
9 = tan-1(zo1)-1an-1( bsencp ) Ec. S
y
03
a +bcos<p
donde:
YoJ
= y
e
cas
.B"
z
03
= z -c sen W
Ec. 6
y el punto P de coordenadas (y, z) es el punto final en el cual se desea que esté el efector. Por ejemplo, si se desea que el efector del
manipulador llegue al punto P(10.66, 10.04), entonces haciendo p=30° y a=b=c=5 se tiene que:
Figura 1. Manipulador de tres grados de libertad
fP1
= 20.2191039°
0
1
= 39.6767976°
()3
= 20 .2191039°
(/)4
= 39.6767976°
'P2
=-20.2191039°
()z
= 60.095901°
()3
=-20 .2191039°
(/J4
= 60.095901°
simultáneamente. Para disei'lar el controlador difuso se dividió en dos partes: una de acercamiento y otra de aproximación fina. En la etapa de
acercamiento se busca que los 3 eslabones del manipulador (Figura 1), obtengan
Al acotar el problema de esta forma, se
pueden llegar a encontrar hasta cuatro orientaciones distintas para un mismo ángulo /3.
El Inconveniente de intentar obtener la Solución a la Cinemática Inversa de esta manera consiste en que puede llegar a no haber una solución al
problema para un valor determinado
de .B. debido a que para esa orientación
específica del eslabón 3 el manipulador no pueda alcanzar el punto deseado con su efector.
DISEÑO DEL CONTROLADOR OIFUSO
Para el diseño del controlador, primero es necesario definir de manera lógica y con palabras, la forma en que los seres humanos movemos nuestros
brazos, antebrazos y muñecas. Esto es para facilitar la codificación de un conjunto de reglas difusas para un manipulador de geometrfa similar al brazo
humano (5). Cuando un niño toma un objeto, primero, orienta su tronco, luego acerca su brazo, y por último mueve la muf'leca para tomar el objeto.
Estos movimientos debido a la "experiencia" que se va tomando , se realizan
una orientación que acerque al manipulador y que el efector pueda alcanzar un punto específico deseado en la etapa de aproximación fina.
Controlador de Acercamiento
El Controlador Difuso de Acercamiento define la orientación previa del manipulador con respecto al punto final deseado para el efector, de tal manera
que se proporcionen los valores de los ángulos para los 3 eslabones. En la
Tabla 1 se muestran las variables de entrada y
salida que se utilizan para el controlador difuso de acercamiento.
El segmento OP es la distancia que existe
del origen a P(x,y). El ángulo 'Peri es el ángulo que define la posición actual del eslabón n, mientras que tpp es el ángulo
del segmento OP.
Los ángulos 6<p, q>en y el ángulo <pp, determinan sí el vector OP tiene la misma orientación que el eslabón en cuestión. La variable
de entrada r determina si el punto final del eslabón está o no cercano al origen del eslabón. La variable de
salida Y'determina el movimiento del eslabón, ya sea en sentido positivo, en sentido negativo o sin cambios.
 219
219

T bla 1.Variables de entrada
y
de salida.
|
Variables de entrada:
|
|
9Wi
|
|
|
|
|
|
.d9'-
|
|
|
r
|
|
|

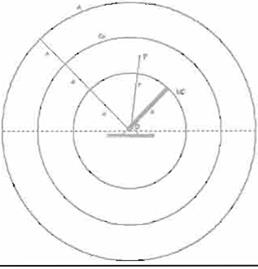 En la Figura 2 se puede ver de manera gráfica las variables de entrada medidas para el eslabón 1, mientras que en Ja Figura 3, se muestran la
disposición de las variables de entrada y las funciones de pertenencia para todos los eslabones diferentes del eslabón con origen fijo.
En la Figura 2 se puede ver de manera gráfica las variables de entrada medidas para el eslabón 1, mientras que en Ja Figura 3, se muestran la
disposición de las variables de entrada y las funciones de pertenencia para todos los eslabones diferentes del eslabón con origen fijo.
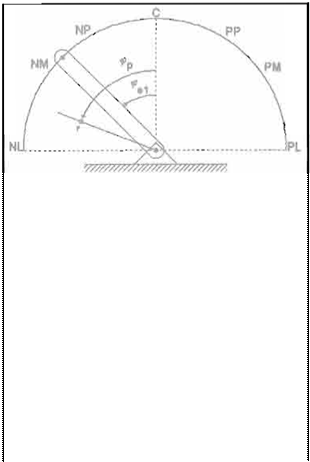
-¡gura
2.
Variables
de
entrada
pan:
eslabón
1.
e
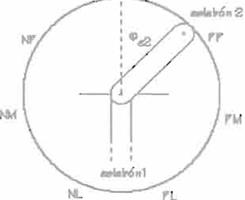
Figura
3.
Varfabtes para los
Eslabones.
Conjuntos Difusos
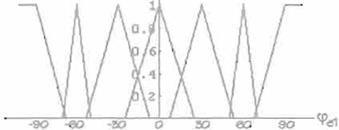
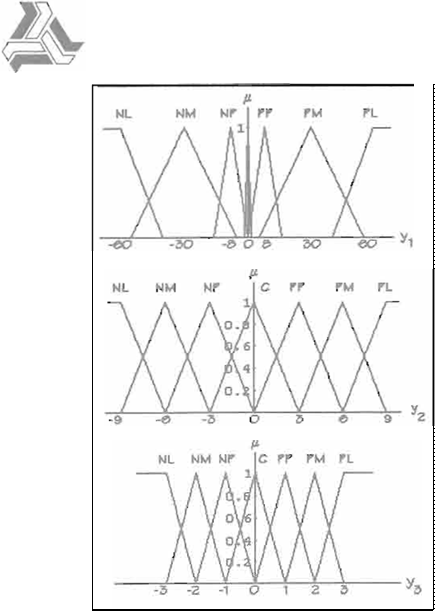
La Figura 4 ilustra las funciones de pertenencia para los ángulos <pe1. 'Pe2 y 'Pe.J, donde, como puede verse, se ha limitado el
movimiento del eslabón 1 de 0° a 90° mientras que a los eslabones 2 y 3 se les permite moverse desde
-180º a 180º. Las funciones de pertenencia
están igualmente espaciadas debido a que lo único que nos interesa es monítorear la posición del eslabón (6).
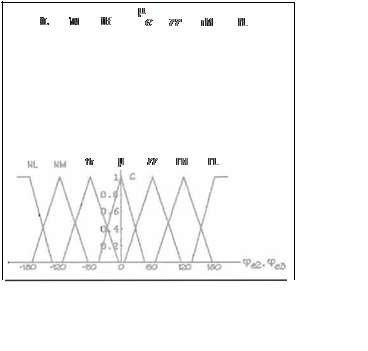
Las funciones de pertenencia de 6<p1, 6<p2 y
 <p3 se encuentran en la Figura 5, donde puede notarse que cuanto más cercanas están a cero,
<p3 se encuentran en la Figura 5, donde puede notarse que cuanto más cercanas están a cero,
Fi
gura 4. Func o :fe Pertenencia para
lo
ángulos de los eslabones.
 220
220

más estrechas son. Esto debe hacerse para que el funcionamiento del controlador difuso sea más fino y además para pennitir la convergencia del mismo.
Cabe mencionar también que el dominio de 6q>1 va de -180° a 180° mientras que para Aq>2 y A<p3 va de -360° a 360° para poder detectar
diferencias grandes entre el ángulo del eslabón y el del vector OP.
En la Figura 6 se muestran las gráficas de las funciones de pertenencia para las variables r1. r2 y f3 que miden la proximidad del
punto P(x,y) con respecto al origen del eslabón en cuestión. Con estas funciones de pertenencia, el controlador difuso de acercamiento puede
saber si es necesario alejar o acercar al eslabón y determinar el movimiento necesario. Como se puede ver, sólo se detennina si el punto en cuestión
está: muy cercano, cercano o alejado del origen del eslabón, lo cual determina la lógica de movimiento dado por las reglas de inferencia que serán
mostradas en la siguiente sección.
En el caso ·de la Figura 7, se ajustaron las funciones de pertenencia para que dicho eslabón se orientara lo más posible al punto al cual se desea que
llegue el efector, lo cual facilitará en gran medida el trabajo del controlador de aproximación .

JI.
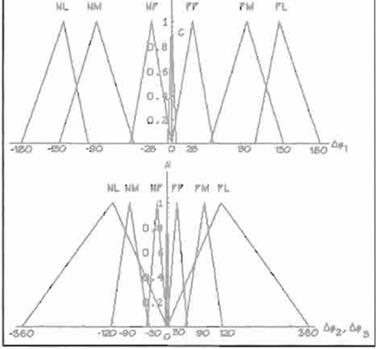
Figura 5. Funciones de Pertenencia para Aq> ,
Aq>2 y A<p3.
Quizás el ajuste de las funciones de pertenencia del sistema sea lo que lleve más tiempo en el dlseí'\o de sistemas difusos. Sin embargo, pueden
utilizarse técnicas de optimización como Algoritmo Genético o RNA, para el ajuste de dichas funciones en el dominio de cada variable.

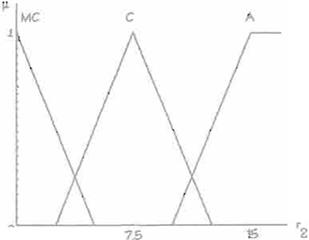
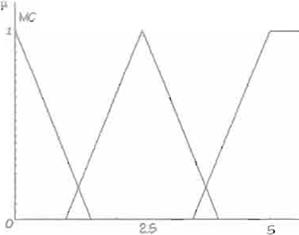 f gura 6. Funciones de Pertenencia para n,
f gura 6. Funciones de Pertenencia para n,
r2 y r3
 221
221

|
'Pen =PP,
q>en=PM y
<i>en=PL
|
. . -
|
|
. r
·..- "( :.
|
: ... ..
|
|
''MC
|
.Ce
|
A
|
|
.. cp
1 .
|
PL
|
e
|
NP
|
NL
|
|
PM
|
pp
|
e
|
NM
|
|
PP.
|
NL
|
Nl
|
NP
|
|
e
|
PL
|
NM
|
e
|
|
NP
|
NM
|
NP
|
PP
|
|
NM
|
NP
|
e
|
PM
|
|
NL
|
|
|
|
|
|
|
|
|
|
|
|
|
Figura 7.Funciones de Pertenencia para las salidas y1 , y2 y y3.
Reglas deInferencia
A continuación se define la terminología usada en las matrices FAM:
<pen =C
•
 PL
PL
• PM
• pp
• e
• NP
• NM
• NL
• MC
• Ce
• A
Positivo Largo Positivo Mediano Positivo Pequeí'lo Cero
Negativo Pequeo Negativo Mediano Negativo Largo Muy Cercano Cercano
Alejado

|
|
. .
|
.. r. ..
. . .
|
. . .
|
|
MC
|
Ce
|
:K·
'
|
|
Áq>:
|
Pl
|
e
|
NP
|
NL
|
|
PM
|
pp
|
e
|
NM
|
|
PP
|
PM
|
pp
|
NP
|
|
e
|
PL
|
PM
|
e
|
|
NP
|
NM
|
NP
|
pp
|
|
·NM
|
NP
|
e
|
PM
|
|
NL
|
e
|
pp
|
Pl
|
|
|
Para cualquier valor de VJoo, si r= MC esto lmpllca que el punto final del efector se encuentra cercano al origen del eslabón en cuestión, por lo cual la
salida "y" se escoge
para que el eslabón se aleje de ese punto, tratando siempre de que Aq;i sea positivo o negativo largo para que el manipulador pueda alcanzar
dicho punto, definiéndose:
Las reglas de inferencia se presentan en las
matrices FAM que siguen en funcíón del valor de 'Pen :
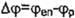 Ec. 7
Ec. 7
De igual manera para cualquier valor de f/Jsn,
si r= Ce esto significa que el punto no está muy
 222
222
••••• •,-•• •• •• •• • • • - • • • -• -•• • •• - ·- ·- - 0 0 •• • •• • -• • •• '" • U> • O U U u •• •

cercano al origen del eslabón en cuestión pero tampoco está demasiado alejado por lo cual se desea que la sallda "y" mueva al eslabón de tal manera que
esté parcialmente orientado en la dirección del punto final del efector.
En el otro caso en el que r=A, se deduce que el punto final del efector está muy alejado del eslabón en cuestión, por lo cual manda una senal de
control que mueva al eslabón de tal manera que se oriente en Ja misma dirección
que la del punto final del efector, para que el manipulador pueda tener el máximo alcance en su espacio de trabajo.
Método de Defuzzificación.
Para este controlador se decidió utilizar el Método del Centroide para ta defuzztficación de ta salida debido a que este método logra obtener una
salida que toma en cuenta las contribuciones de todas y cada una de las reglas de inferencia del sistema (7). Este método está descrito por la
siguiente ecuación:
p
_ LY 1µs(Y¡)
B
= J=I Ec. 8
f µB(Y ¡)
J=1
donde:
B=
centroide del área difusa (salida real).
n
=
·
centroide del área de la función de
pertenencia de salida j.
µ
8
(y.J=valor
de pertenencia del elemento producto de la inferencia difusa .
p=
número de conjuntos difusos de salida .
Controlador de Aproximación
El controlador de aproximación es en sí un algoritmo que busca cambiar los ángulos de los 3 eslabones para lograr que el efector alcance
el punto deseado. Primeramente se utiliza el ángulo final f3 del controlador de acercamiento para solucionar la cinemática Inversa y mueve
at manipulador. Si no encuentra solución, entonces cambia el valor de este ángulo y trata de encontrar una solución para los otros dos
estabones. Si el punto P deseado está fuera del
espacio de trabajo del manipulador, el controlador de aproximación simplemente orienta a los eslabones en la misma dirección del vector OP y enciende
una bandera.
SIMU
LACI
ÓN
Para la simulación en computadora
primeramente se realizó un programa en lenguaje eque contiene procedimientos para el
manejo de sistemas difusos. Asimismo se requiere que el usuario determine ciertas cantidades constantes tales como el número de variables de entrada y
salida del sistema, número y especificación de las funciones de pertenencia de todos los conjuntos difusos del sistema.
RESULTADOS
En el presente inciso se presentan los resultados de la simulación, mediante gráficas que ilustran la evolución de la orientación del manipulador. Se
realizaron diferentes pruebas, cambiando la condición inicial del manipulador y especificando puntos P(x,y) diferentes dentro y fuera del
espacio de trabajo (Figura 8 y Figura 9).
El controlador puede posicionar el efector del manipulador en el punto deseado
 independientemente de las condiciones inlciales. De acuerdo a los resultados
independientemente de las condiciones inlciales. De acuerdo a los resultados
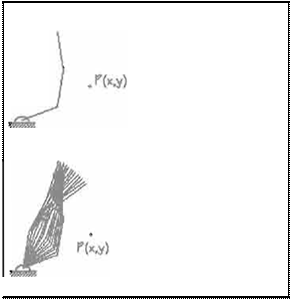
 Figura 8. Evaluación del manipulador.
Figura 8. Evaluación del manipulador.
 223
223



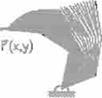 F
i
gura 9. Evaluación del
F
i
gura 9. Evaluación del
manipulador.
obtenidos, cuando el manipulador no puede alcanzar el punto, éste simplemente se orienta en esa dirección. Cuando el punto deseado está muy cercano al
origen del eslabón fijo, éste último se aleja del punto dependiendo de su cercanra para pennitir el plegado de los otros dos eslabones para alcanzar su
objetivo.
CONCLUSIONES
La ventaja del razonamiento que se utilizó en este trabajo para el diseño del controlador puede aplicarse para el diseño de controladores difusos de
manipuladores con otras configuraciones. De esta forma se pueden obtener sistemas de control de robots sencillos de implantar, mantener y comprender
sin ser neceS<iria la obtención del modelo matemático del brazo a controlar.
Uno de los principales problemas de los sistemas difusos es el ajuste y puesta a punto de la ubicación de las funciones de pertenencia sobre todo
cuando se manejan varias entradas, debido a que para determinados estados suelen activarse reglas no deseadas, por estar mal ajustadas dichas funciones
de pertenencia. Los
últimos avances presentan el uso de técnicas de optimización y búsqueda como RNA y Algoritmo Genético. Estas técnicas ajustan la ubicación de estas
funciones hasta alcanzar un nivel óptimo.
La utilización de la Lógica Difusa es una
solución viable para el dlsel'io y aplicación de controladores en diferentes áreas de la ingeniería debido a:
• La sencillez de su estructura, porque su implantación se parece más al lenguaje natural humano.
• La facilidad de ajuste y modificación del controlador.
• Robustez del controlador.
REFERENCIAS
1. Schwartz, D., Klit, G., Japan goes Fuzzy,
IEEE
Spectrum,
USA, julio, 1992.
2. Cox, E., Fuzzy Fundamentars, IEEE Spectrum, USA, octubre 1992.
3. Omron Electronics, lnc., Fuzzy Logíc a 21st Century Techno/ogy, USA, Technicaf lnformatíon , 1991.
4 . Spong, M ., Vidyasagar, M., Robot Dynamics and Control, USA, John Wltey & Sons, 1989.
5. Jamshidí, M., Vadice, N., Ross, T., Ftrz:zy
Logíc and control,
USA, Prentice Hall, 1993.
6. Cox. E., The Fuzzy Systems Handbook,
USA, Academic Press, lnc.• 1994.
7. Kosko, B., Neural Nefworl<s and Fuzzy Systems, USA, Prentice Hall. 1992.
![]() SOLUCIÓN DEL PROBLEMA DE LA CINEMATICA INVERSA EN ROBÓTICA UTILIZANDO LÓGICA DIFUSA
SOLUCIÓN DEL PROBLEMA DE LA CINEMATICA INVERSA EN ROBÓTICA UTILIZANDO LÓGICA DIFUSA


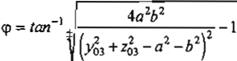
 Ec. 4
Ec. 4


 En la Figura 2 se puede ver de manera gráfica las variables de entrada medidas para el eslabón 1, mientras que en Ja Figura 3, se muestran la
disposición de las variables de entrada y las funciones de pertenencia para todos los eslabones diferentes del eslabón con origen fijo.
En la Figura 2 se puede ver de manera gráfica las variables de entrada medidas para el eslabón 1, mientras que en Ja Figura 3, se muestran la
disposición de las variables de entrada y las funciones de pertenencia para todos los eslabones diferentes del eslabón con origen fijo.


 <p3 se encuentran en la Figura 5, donde puede notarse que cuanto más cercanas están a cero,
<p3 se encuentran en la Figura 5, donde puede notarse que cuanto más cercanas están a cero,





 f gura 6. Funciones de Pertenencia para n,
f gura 6. Funciones de Pertenencia para n,


 independientemente de las condiciones inlciales. De acuerdo a los resultados
independientemente de las condiciones inlciales. De acuerdo a los resultados

 Figura 8. Evaluación del manipulador.
Figura 8. Evaluación del manipulador.



 F
i
gura 9. Evaluación del
F
i
gura 9. Evaluación del