IMPLEMENTACION DE UNA RED NEURONAL CELULAR EN UNA COMPUTADORA ÓPTICA

Eduardo Gómez.ffamirez, Víctor Ramos-Viterbo, Moisés Aloncastre-Ml randa,

Alejandro Flores-Mónda y Agustín SAnchoz De Taglo

uboratorio del Centro deInvestigación, Universidad La Sallo

RESUMEN

En la última década se han desarrollado una gran cantidad de algoritmos de Redes Neuronales Artificiales para diferentes tareas. Uno de los más importantes es el de Redes Neuronales Celulares (RNC), el cual se ha empleado principalmente para el reconocimiento y procesamiento de imágenes debido a su naturaleza paralela y que puede ser implementado en circuitos VLSf. Existen varios algoritmos de redes neuronales que también tienen naturaleza paralela como el modelo de Hopfíeld y. BAM que han sido implementados en una computadora óptica. En este trabajo se presenta una implantación del algoritmo de RNC en una computadora óptica.

ABSTRACT

On the last decade a great quantity of algorithms of Artificial Neural Networks for different purposes have been developed. One of the most important are CeUular Neural Networks {CNN), which has been used mainly fer the image processing and pattern recognition because of its parallel nature and because it could be implemented on VLSI circuits. There are a few works using optical computers like Hopfield and BAM Networks. The current paper show an implementation of the algorithm of CNN in an optical computer.

INTRODUCCIÓN

Las Redes Neuronales Celulares (RNC} han tenido un gran desarrollo principalmente en implantaciones para el procesamiento y reconocimiento de imágenes. Una de las razones principales es su naturaleza paralela y la sencillez de su algoritmo. La naturaleza paralela de las redes neuronales ha sido aprovechada por otro tipo de tecnologías para su aplicación. Algunas de ellas son en VLSI y otras de ellas utilizando nuevos desarrollos como es el caso de la computación óptica. Esta herramienta ha sido utilizada para la implantación de redes neuronales como Hopfield y Kanerva (1) para el procesamiento y reconocimiento de patrones. En este trabajo se presenta la implantación de una red neuronal celular en una computadora óptica. Se incluyen algunos ejemplos de procesamiento de imágenes.

El artículo está estructurado de la siguiente forma: en la primera parte se hace una descripción del algoritmo de RNC, en la

segunda se hace una breve descripción de lo que es computación óptica y arquitectura principal. En la siguiente parte se describe un ejemplo de procesamiento de imágenes y por último, conclusiones y trabajo futuro.

RED NEURONAL CELULAR

Desde sus orígenes en 1987 las redes neuronales celulares surgen como un algoritmo muy poderoso, y hoy en día son varios los grupos de investigación en esta área. Este desarrollo ha sido tal, que en Europa cada dos años se hace un congreso dedicado a este algoritmo. Éste surgió en los laboratorios del Profesor León Chua en Berkeley (2,3).

Como se definió en sus orígenes una RNC es un arreglo idéntico, no lineal de circuitos dinámicos simples colocados en forma bidimensional (2). Este arreglo puede ser de diferentes tipos dependiendo de la forma de su conectividad o de la forma de su vecindad.

299

MODELO MATEMÁTICO

El modelo matemático simplificado que define este arreglo es el siguiente {4):

La salida Ye se obtiene aplicando la Ec. 2. Esta ecuación limita el estado de la salida en el rango {-1,1], de la misma forma en que limitan las funciones de activación en modelos clasicos de redes neuronales. (Figura 1).

MODELO MATEMÁTICO DISCRETO

donde:

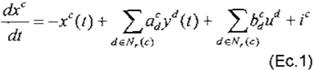y "( t ) = ±(lx'(t) + tl-lx'(t) -1)

(Ec.2)

El modelo matematico descrito anteriormente puede ser representado de la siguiente forma:.

c/x c

-= -x' (t) + k (Ec.3)

dt

• La variable xc representa el estado de la célula c, { la salida y uc su entrada.

El estado de cada célula es controlado por las entradas y las salidas de células adyacentes

donde:

k = ¿a/ (t) + ·¿);ud + ¡"

d EN , ( c ) d E N,( c)

1

dentro de una r-vecindad N,(c). Las salidas se retroalimentan multiplicadas por tos coeficientes ad y las entradas son multiplicadas por parámetros de control bd. El valor de ¡e es constante y se utiliza para ajustar el umbral . Estos coeficientes son invariables traslacionalmente y serán denominados como

modelo 2 .

' --4.á------- 1

*

X

1L_:1 t,_ 1

Como el estado final del sistema se obtiene evaluando x(oo), el modelo puede ser simplificado a:

<i< .v,1,·) dEN, Cc)

(Ec.4)

Algunos autores consideran también una modificación en la salida (Ec. 2). de la siguiente forma (4):

y c ( k ) = f (x'.( k - 1))

/ (k) = { 1 si xc( k -l) > O (Ec.5)

-1 si x('( k - 1) < 0

1

"f -1

1

i -0.5

-1

Fi gura 1 . Func.ón e salida.

Este coeficiente es equivalente al input bias

en otras redes.

2 A todos estos coeficientes se les conoce como template.

Sin embargo, la simplificación realizada (Ec.

4) puede utiliz.arse con la función de Ec. 2 (6).

COMPUTACIÓN ÓP'!"ICA

A diferencia de la tecnología tradicional de computadoras donde el proceso se hace

manipulando electrones. En una computadora óptica se utilizan fotones. El principal motivo es utilizar las características naturales de la luz: su

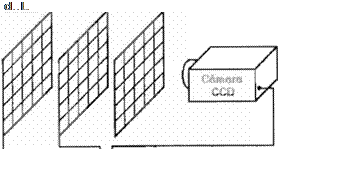
velocidad y naturaleza paralela. Una de las principales arquitecturas utilizadas es la siguiente, que considera bésicamente tres partes (5):

300

Fuente

Emisore:.

Pantnltn

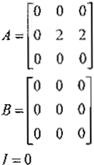do Tra.• ·,e

Figura 2. ,..... - una Computadora

Óptica.

1) Fuente emisora de luz, en donde se despliega la imagen a ser transformada .

Los Resultados en simulación a la primera iteración se muestran en la Figura 4 y para la tercera y quinta iterac ión se muestran en las Figuras 5 y 6. Los resultados para los mismos pasos utilizando la computadora óptica se muestran en las gráficas de las Figuras 7 y 8.

En el caso de que se utilice un modelo en el cual los coeficientes de la matriz sean números negativos, como el siguiente:

A = [-5 -5 5]

1

o -05 o

2) El modelo se despliega en un modulador espacial de luz. En esta parte se puede utilizar un acetato o un Oatashow.

3) El resultado se visualiza en una pantalla. Esta pantalla puede ser un vidrio traslúcido de tal forma que este resultado pueda ser capturado por una cámara

eco, para su retroalimentación ya sea

en la entrada o en el modulador. Esta arquitectura puede verse en la Figura 2.

La multiplicación de las matrices por la entrada se obtiene utilizando la técnica de Shadow Casting (5), y los resultados de la transformación son puntos en intensidades de

luz. Este resultado es capturado con una cámara eco, y retroalimentado utilizando una

PC. Esta arquitectura fue implementada en el laboratorio del Centro de Investigación (5,6), y actualmente se está trabajando en el desarrollo de mejores etapas (7), ya sea para aumentar resolución o para incrementar la velocidad del procesamiento que se realiza en la computadora (PC).

EJEMPLOS

Se utilizó la imagen de la ·Figura 3 y las matrices A y B siguientes (3):

B=[

o o o

I := O

se requiere separar los valores de la matriz en valores negativos y p0sitivos. Después de esto se aplica el proceso equivalente a la cenvolución de la misma forma que en el ejemplo 1. De esta forma se obtuvieron las Figuras 11 y 13 para la parte negativa. y 12 y 14 para la parte positiva. Finalmente estos dos resultados se suman para obtener la salida correcta. (Figura 15).

Como se puede observar en las figuras se obtienen los mismos resultados en tos valores de simulación. como los obtenidos utilizando la computadora óptica.

ANÁLISIS DE RESULTADOS Y

CONCLUSIONES

La Computación Óptica ofrece importantes ventajas en cuanto a la velocidad, procesamiento en paralelo y manipulación de señales de tipo binario. Dependiendo de los avances que se puedan desarrollar para

301

Fi gura 3. Imagen Origina!

Simulación Computndor:.i Óptica

Figura 4. Prim ra !t r:aclón. Figura 7 . Primera Iteración

Flgum 6. Segundi:a ttan:ac:ión. Fi gura 8. Segunda Iteración

FJgura 6. T rcera tterución Figura 9. Tercera lter.ación

mejorar las interfases de entrada de datos y procesamiento, esta arquitectura puede llegar a sustituir las arquitecturas convencionales que manipulan electrones. En este caso la implantación de algoritmos de redes neuronales artificiales que funcionan en forma paralela es casi automático, como lo fue para los casos que se han analizado de Hopfield, Kanerva y

en este último de redes neuronales celulares. A pesar de que todavía no es posible disponer de interfases ópticas para su manejo. la computadora óptica puede reconocer y procesar imágenes utilizando una red neuronal celular.

302

Figura 10. Imagen Original.

Simulación

Computadora Óptica

Figura 11.Estado nogativo para la primera

iteración .

Figura 13. Estado nogativo para la primor itonación.

Figura 12.Estado positivo para la !)rimora iteración.

Figura 14.Estado positivo para 12 primera itor.ición.

Figuro 16. Unión de las partos positiva y negativa.

303