 C
ONTROL ADAPTABLE BASADO EN EL ANÁLISIS
oe
PASIVlDAD PARA UN ROB01
.
C
ONTROL ADAPTABLE BASADO EN EL ANÁLISIS
oe
PASIVlDAD PARA UN ROB01
.
MANIPULADOR RIGIOO DE DOS GRADOS DE LIBERTAD
Ma. del Cannen Lule-Capintoyro y Hugo G. GQnzález-Hernándoz Laboratorio dol Centro do lnvostigaelón, Universidad La Sallo
RESUMEN
El desarrollo de técnicas efectivas de control representa un paso importante en aplicaciones de robótica, pues éstas se ven afectadas por
incertidumbres paramétricas. Una alternativa para controlar un robot manipulador del cual no se conoce el modelo dinámico nominal, es el diseñar un
control adaptable. En este artículo se presenta el diseño basado en análisis de pasividad y bajo el criterio de Lyapunov, de un controladaptable para
un robot manipulador rígido con articulaciones rotacionales de dos grados de libertad con incertidumbre paramétrica. Se prueba este controlador
realizando el seguimiento de una trayectoria deseada.
ABSTRACT
The development of efectiva control techniques represents a great deal in robotics applicatíons because there exist parametric uncertainty. Adaptive
control techniques offer an alternatíve strategy for this problem. In this paper we show a passivity analysis based design of an adaptive control far a
two-degree-of-freedom rigid manipulator in such a way that this controller allows us to have global asymptotic stability for tracking a desired
trajectory.
I
NTRODUCCIÓN
estimados y los reales (error de predicción) o el error entre la salida deseada y la salida actual
Cuando no se conoce por completo el modelo nominal1 de la dinámica del robot manipulador. es decir, que existen incertidumbres en algunos o todos los
elementos que la componen. se propone compensar este desconocimiento paramétrico con estrategias adaptables para su control, pues tienen !a ventaja de
que el mecanismo de adaptación extrae información del sistema
tratando de llegar al conocimiento de éste por completo en un tiempo finito teniendo como referencia el error de seguimiento.
Las leyes de control adaptable pueden ser clasificadas de acuerdo a su objetivo de control y la señal que dirige la ley de sintonización de los
parámetros. El objetivo de control determina la estructura en el controlador de los parámetros. los cuales van a ser sintonizados
del sistema (error de seguimiento).
En este artículo se discutira el diseño de un controlador adaptable de dinámica inversa, también llamado par calculado pasivo, cuyo
objetivo de control es, además de la linealización2 del sistema. preservar las propiedades de pasiv idad de la dinámica del manipulador en lazo
cerrado.
La presentación está organizada de la siguiente forma: en la primera sección se presentan algunas definiciones que serán de utilidad para las pruebas
de estabilidad y análisis de pasividad; en la segunda sección se presenta la derivación de las ecuaciones de la dinámica del manipulador
mediante las ecuaciones de Euler-Lagrange; en la tercera sección una vista rápida al controlador Par
en línea. La ley de sintonización o estimación,
en cambio, puede ser dirigida por una señal que mida, o bien el error entre los parámetros

Sistema altamente no lineal.
2 Es un caso especial de retroalimentación para la linealización de un sistema no lineal, esto es. obtener un sistema en lazo cerrado el cual es lineal
y desacoplado.
 311
311

calculado
pasWo
tanto para el caso de parámetros conocidos y el diseño del controlador adaptable para parámetros desconocidos; y por último, en la cuarta sección se
presenta la simulación de un caso de una configuración específica para un manipulador de 2 grados de libertad en el seguimiento de una trayectoria
dada.
1.
NOTACIÓN Y TERMINOLOGÍA
En principio se presenta la notación y algunas definiciones, lemas y teoremas que se manejaran a lo largo de los diferentes análisis y derivaciones.
R.. denota el conjunto de los números reales no negativos.
Rº denota el espacio vectorial n-dimensíonal sobre los reales.
= se entiende como igual por definición.
Dl
es equivalente a df Idx sup significa supremo de.
Definición 1.
La norma euclidiana está definida como:
1
1N1= (t,1x,1')'
Definición
3
.
Una función f :R" -7 Rm es continua si
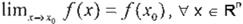
Definición
4.
Una función f es uniformemente continua si 3 k>O, k ER, tal que:
l:f(x)l S k < 00
ld ;x)" k <oo, 'rlx E R"
esto es que f E L.., y Dx f E L..,.
Lema 1
.
Considere las funciones continuas y diferenciab!es x:R.-7Rm y y:R.-tR•. Defínase una función V : Rm-7R. dada por :
V(x,y) = xT K .X + y ;::: o
K = KT > O E Rmxm
Si 3 una función z:R-4U, U es un subespacio de Rm de dimensión i(m), tal que:
V(x,y)
= -zrK2 z S O
K
1
::::: K: > o E R/IUlll
entonces: x E Lx., y E L..,, z E L1
Abusando de la notación de tal forma que, si H(s) es una función de transferencia en
s de una función
Definición 2.
El espacio lineal L2 es el conjunto de las funciones f : R -7 R", tal que:
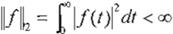
El espacio lineal es el conjunto de las funciones f : R.-t R", tal que:
ll!IL spjlf;col < 00
1
variable compleja
(transformable en Laplace) h(t) y r(t) es una función del tiempo, entonces H(s)r estará dada por (h*r:)(t), donde .. denota el producto de convolución.
Con esta notación tenemos que:
Lema
2. (2) Sea
e = H(s)r
donde H(s) es una función de tranferencia exponencialmente estable de dimensión nxm y estrictamente propia
donde 11 12 es la norma L11
y 11 1.. es la norma
Entonces: r E Ln2 => e E L0
n Lº... Dxe E Lº2;
2
Lº.,, lo que implica que ambos espacios son espacios lineales normados.
e es continua y e-tO, t--7«>. Además r-40, t-400,
entonces Dxe-+O.
Si r E L'\,,, entonces e E Ln"' y Dxe E Lºoo·
 312
312
Definición 5.
Un mapeo X-7Y es pasivo si y
solamente si:
una función cuadrática del vector DxQ de la forma:
(xlY)r: ( Xr yd t -B
> O, VT
K
= tL"
1,)
H;.¡(q)q,t¡
J
= tfH(q)q (Ec. 2)
Teorem
a
de Barbalath.
Si una función diferenciable f(t) tiene un límite finito cuando t-700 si Oxf(t) es uniformente continua.
Entonces Dx f(t)-+0, t-7co.
f{t} es continua en [O,co) si V t1 O, 'r/ R > O 3
ri(R, t1) > O, tal que 'rf t ::? O, ft- t,l<ri. entonces
donde H{q) es una matriz mcn. simétrica y positiva definida para cada qeR" llamada matriz de inercia. En este caso, q son las posiciones de la
articulación.
Las ecuaciones de Euler-Lagrange para un sistema dado pueden ser obtenidas, tal que:
11
lf(t) - f(t1)I < R.
f(t) es uniformente continua si D/(t} está
acotada.
Corol
ario
(Barbalath
usando
el
criterio
de
Lyapunov
)
.
Sea la función escalar V(x ,t}, tal que:
/) V(x,t)
¿
{3
> o
ii)
dV(x,t)
l
dt
s
O
iii)
dV(x,t)ldt
es uniformemente continua
dV
(x
,
t)ldt O,
t-+
co.
2.
DINÁMICA
oe
MANIPULADORES
RÍGIDOS.
Utilizando las ecuaciones de Euler-Lagrange, tal que (2):
d a r
a L
L
= K - P = 1L,h,;{q)q/¡1- P( q)
i,j
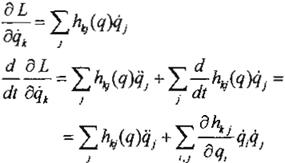 Entonces:
Entonces:
(Ec. 3)
----='t
dt
8 aq
(Ec. 1)
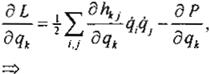
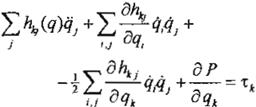 k= 1,...,n (Ec. 4)
k= 1,...,n (Ec. 4)
Intercambiando el orden de las sumatorias
donde q = (q1, ..., Qn)T es el conjunto de coordenadas generalizadas del manipulador, L
es el lagrangiano definido como la diferencia entre la energía cinética K y la energía potencial P,. y 't = (-i1, ..., -rn)T es el
vector de fuerzas generalizadas que actúan sobre el sistema. Un caso especial importante es en el cual la energía potencial P=P(q) es independiente de
y la energía cinética es
en el segundo término y tomando ventaja de la simetría de la matriz de inercia, entonces:
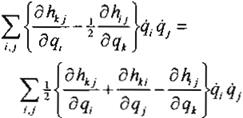 (Ec. 5)
(Ec. 5)
 313
313


 Los coeficientes
Los coeficientes
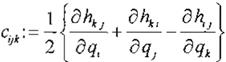
son conocidos como los sfmbolos de Christoffel
(de primer tipo). Si tenemos:
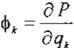 (Ec. 6)
(Ec. 6)
entonces podemos reescribir las ecuaciones de Euler-Lagrange como:
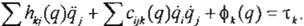
j 1,j
k= 1,...,n (Ec. 7)
Podemos observar que hay tres tipos de términos dentro de estas ecuaciones. El primero involucra la segunda derivada de las coordenadas generalizadas.
El segundo son términos cuadráticos en la primera derivada de q, donde los coeficientes dependen de q. tstos son clasificados de 2
tipos, los que involucran
el producto de e¡; llamados de fuerza
centrifuga
y los que involucran productos del
Cuadro 1
.
Propiodades Fundamentales.
tipo i¡; i¡
1
donde i;t: j, son llamados términos de
Cono/is.
El tercer tipo son los que involucran sólo a q pero no a sus derivadas. Comúnmente
(7) se escribe de la forma:
H(q
)q
+ C(q,q)t¡ + g(q) = -c (Ec. 8)
donde los elementos del segundo término son definidos como:
n
coeficiente como un parámetro separado, se
tiene una relación lineal dada por:
H(q)ij
+ C(q,é¡)q + g(q) = Y(q,q ,i¡)S = -r
(Ec. 10}
donde Y(q,q,q) es una matriz de nxr de
funciones conocidas, llamado también regresor,
y
e es un vector r-dimensional de parámetros.
c
kJ :=
.L
c
!lk(q)q
·=•
(Ec. 9)
Además, sabemos que la Ec. 8 es un mapeo pasivo de 't-+ q (1) en lazo abierto.
 Propiedades
Fund.amontales
Propiedades
Fund.amontales
éstas se muestran en el cuadro 1. Además, todos los parámetros constantes tales como longitudes y masas de los eslabones, momentos de inercia, etc.
aparecen como coeficentes de funciones conocidas de las coordenadas generalizadas. Definiendo cada
3.
CONTROL PAR CALCULADO PASIVO Y
PAR CALCULADO PASIVO ADAPTABLE.
Hasta aquí se presenta la dinámica de un manipulador de n grados de libertad. El problema que se presenta en forma general en robótica es el seguimiento de una trayectoria
 314
314
deseada por parte del manipulador. por lo que se necesita encontrar un cierto controlador, que pennita llevar a cabo este objetivo en el menor
trayectorias del error asintóticamente a cero.
convergerán
tiempo posible, con una cierta exactitud y manteniendo o haciendo a! sistema estable según sea el caso.
La noción de estabilidad es con respecto a un punto, el cual generalmente es el punto de equi!ibrio3 del sistema en una cierta vecindad; es por esto
que, el diseño del controlador se
realiza bajo el espacio del error entre las
trayectorias deseadas y las trayectorias que genera el manipulador, pues dado que deseamos que se mantenga en su punto de equilibrio, tenemos que sí el
error queda en su punto de equilibrio, es igual a cero. por lo que la trayectoria generada por el manipulador es igual a la trayectoria deseada.
Dado lo anterior se propone que e! error (s) se define como:
s
= q -q,
{Ec. 11)
q,
= Cfd -a&¡
donde a. es una matriz real, diagonal, definida positiva.
Ahora bien, si hacemos un lazo cerrado con un controlador basado en un controlador PO, el cual permita cancelar las no linealidades, este será definido
como:
1: = H(q)(i:jd - cu'iq) +C(q,é¡)(t¡d -aóq)+
+g(q) - Kds
(Ec. 12}
donde es una matriz diagonal constante definida positiva.
Teorem
a
.
Considere la dinámica del manipulador de n grados de libertad en lazo cerrado con elcontrolador de Ec. 12 definiendo el error como la Ec. 11.
Entonces las

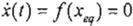 3 Un punto Xeq es un punto de equilibrio siuna vez que x (t) = Xeq. x(t) pennanece en Xeq '<t t. Esto es,
3 Un punto Xeq es un punto de equilibrio siuna vez que x (t) = Xeq. x(t) pennanece en Xeq '<t t. Esto es,
Prueba.
Considera la función candidata de Lyapunov:
V =
t
s
'
H( q)s
Obteniendo la derivada evaluada sobre las trayectorias del error, tomando en cuenta las propiedades sobre los términos de la ecuación de la dinámica
delmanipulador, resulta como:
. r
V
=-s
Kd
s
Entonces utilizando et teorema de Lyapunov resulta que s = &¡_ +a óq -) O en el limite ói¡ -) o, óq -)
o .
Cuando se habla de este tipo de controladores se deben tomar en cuenta ciertas condiciones iniciales; la más importante es el conocimiento exacto de
toda la estructura, siendo esta situación casi nula la mayor parte de las veces en la práctica, pues existe incertidumbre de los parámetros de la
dinámica.
Dada esta situación se presentan 2 posibles soluciones, una de ellas es la utilización de un controladaptable, el cual estima los parámetros de la
planta hasta llegar a un comportamiento parecido o igual al del sistema deseado; la otra es la utilización de un control robusto, compone
la estructura del controlador dependiendo de ciertas cotas conocidas del sistema. El control adaptable tiene un mayor desempeño que el controlador
robusto, puesto que el primero mejora su desempeño en línea de acuerdo a las condiciones del tiempo t, mientras que el segundo mantiene un
desempeño fijo para cualquier tiempo.
Dentro del control adaptable se distinguen dos estructuras: el control adaptable directo e indirecto.
En el caso del control adaptable directo, la estimación se realiza sobre los parámetros del control; mientras que para el caso del control adaptable
indirecto se estima primero el sistema, y posteriormente se calcula el control bajo el resultado arrojado por el método de
identificación.
 315
315

Para diseñar un control adaptable se requiere acceso al estado del sistema, la parametrización lineal de la planta. y por último. que las no
linealidades puedan ser canceladas cuando los parámetros son conocidos.
Entonces, conociendo lo anterior y para el propósito del presente, se da a continuación la eS1ructura de un control adaptable directo basado en el
control par calculado pasivo visto
anteriormente.
Ahora el objetivo es hacer que la trayectoria real convea a una deseada, sin garantizar que los parámetros estimados converjan a los reales, pero que
permanezcan acotados.
4.
DISEÑO
D
E
CONTROL ADAPTABLE
PARA UN MANIPULADOR DE N GRADOS
DE LIBERTAD.
Teniendo la ecuación
H
(q)q
+tH( q)t¡ +S(q,q)é¡ +g(q) = t
(Ec. 13)
Dado que la estructura de la dinámica no es conocida, se tiene que el control referenciado por -r es de la forma:
/\ ;.. . /\ /\
t =H(q)qr+1 H(q)q,+S(q,q)qr +g(q)-Kd s
(Ec. 14)
Entonces en lazo cerrado, las Ecs. 13 y 14
quedan como:
H
(qXij
-q,)+t
H(qXiJ.-i¡J +S(q,i¡)(q-é¡,)
=
/\
=
Y(q,é¡,éJ,JirXe -
e ) -K"s = Y,.eie -Kd s
(Ec. 15)
Sustituyendo el valor de s queda:
H(q
)s
= -t Íf (q)s +S( q,q)s+ r,:eie - Kd s
(Ec. 16}
Ya encontrado el control, debemos analizar
Lyapunov; para esto, se procederá a un análisis de pasividad aumentando una variable más al control, que funcionará sólo como herramienta matemática, y
la denominaremos con T', cuyo valor es cero. Entonces, el control queda como:
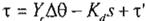 (Ec. 17)
(Ec. 17)
El control en lazo cerrado con la dinámica resulta:
H( q)s
+
t
Íf ( q)s+ S( q,q)s - J;óe
+ Kd s = 1:0
Ahora para la pasividad, debe ser entre la entrada Tº y la salida s
sr
i:
'
=
sr
H
(q)s+ t sr
H(
q
)s
+
+ ?S( q,é¡)s - srr,. e + srKd s
donde
srS(
q
,
q
)s
= O
(t s1H(q )s) = srH(q)s+ tsrH(q)s
dt
Si no existiera el término -sr YrllfJ. el mapeo entre la entrada y la salida seria estrictamente pasivo. Por lo tanto, necesitamos agregar un
término más al control, de tal forma que podamos establecer el mapeo pasivo deseado, pero debido a que no conocemos los parámetros reales, no se puede
introducir tal
cual; esto es, el error parámetrico ti.e es
desconocido. Entonces, se propone una nueva entrada vía la salida de un integrador en el estimado de los parámetros é . esto es:
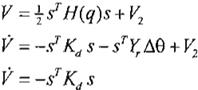
Entonces, conociendo lo anterior, debemos introducir sr Y,Ll& vía é para cancelar los términos que impiden el tener el
mapeo pasivo.
A
Ahora, se tiene a
la estabilidad del nuevo sistema, para lo cual necesitamos obtener o proponer una función de
como un nuevo estado en
el sistema, pero al darse el desconocimiento de
los parámetros, el nuevo estado queda en
 316
316

función de .M, que entra en la función de Lyapunov de forma cuadrática:
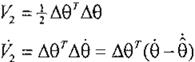
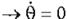
=>
v; = -óe e
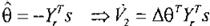
Si V=V+V2, la derivada de V es -srKQS, la cual es O y asegura según lo visto en la sección 1, la estabilidad asintótica global de s
tomando en cuenta que: •
s
= &:¡+a &¡ -+0 en el límite óiJ. -+0,&¡ -+0
Luego, tanto las trayectorias de la posición como las trayectorias de velocidad del manipulador tienden a las trayectorias
deseadas cuando t-+oo.
Por lo que el control queda de la forma :
t :: i':L\9 - Kds
S
= -
r
rrs
(Ec. 18)
donde eR""" >O y reRllO' >O es una matriz de ganancia4 y diagonal.
Teorema.
Considere el control de Ec. 18 en lazo cerrado con la dinámica del manipulador. entonces:
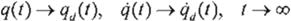
Prueba
:
Sea la función de Lyapunov:
V
=
t{?H( q)s+ óerr-11:10}
V
=
s
r
H(q
)s
+ L\9rr-1(S)+f ?i-l( q)s
H
(q)s
= -t i-l( q)s -S(q,q)s - tia
e = -rrrrs
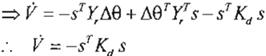

4 que para el desarrollo se tomó como unitaria.
Por el teorema de Lyapunov, dado que
S
= ÓÍ/. +a !iq E [,_ ,
y que si
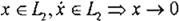
entonces
!iq
4' o, t 4' 00
De la Ec. 15 en lazo cerrado con el control:
H(q)s +
t
H( q)s + S(q,q
)
s
= Y,1:18 - Kd s
1) H( q) > O
ii) H(q) está acotada. iii) S(q,q) está acotada. iv) Kd está acotada.
Para el término Y,68 sabemos que:
V
E Li y V = t {srH(q)s+ L\err-i1:1a}
=> 1:19 E li_
De la ecuación de lazo cerrado con el
control sabemos que s E Li .Ahora dado que V
es acotada por abajo, y empleando el teorema de Barbalath, bajo el criterio de Lyapunov tenemos que:
v o
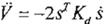
i) s es acotada ii) s es acotada
iii) Kd > O
V
existe y está acotada.
=>
V
= -?Kd s O, s o
y como L\ q O y !l q O, t oo
 317
317

entonces:
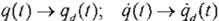
teniendo como q<1, la trayectoria deseada.
Caso Práctico
Para obseNar mejor el fenómeno expuesto anteriormente. se presenta el ejemplo de la simulación del ·comportamiento un robot manipulador rigído de 2.
grados de libertad
(Figura 1) bajo la acción de un control adaptable directo, cuya dínámíca es la siguiente:
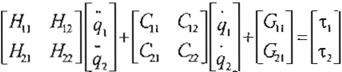
donde:
H
JJ=
m
1
•/
c1
*
fc 1+
m
;
"
(l1
*
!1
+ lc1*lc1 +
2
•
1
1
•/
c
1
•
cos(qi})
+ 11 +l'l
H1
1
=
m
1
•(1
cz"
l
c1
+ l1*lc1*cos(qv) +12
H
11=
H11
H
21
=
(mJ*lc
1
•
l
c1 +
1
1
C
11
=
-m
1
•
1,•1
c1
*
se
n
(qi)*y1
C12
-
-
m
1
*!,
•
1c
2
*
se
n
(qi)*(y
z
+yJ)
C2
1=
111
1
*!,*lc,•sen(q2)*y1
C
22""
O
 lc2
lc2
GJJc:
(m
1
*
l
c
1
+m
2
*
1¡}
*g*
cos(q¡}+
m
1
*
1
c
1
*g*cos(q
1
+
q2)
G11
=
111
¡
•
Jc1*g
"'
cos(q,-1
qi)
siendo:
- q1 y q2 las coordenadas generalizadas, dadas por la pos1c1on de las articulaciones rotacionales del robot manipulador;
- Y1 y y2 como las derivadas de primer orden de
q, y <¡2.;
- m; y 1, es la masa y la longitud, respectivamente, del eslabón i-esfmo;
- lc1 y lc2 son los momentos de inercia de los eslabones 1 y 2 respectivamente;
- 1 1 y 12 son los momentos de inercia de los eslabones 1 y 2 respectivamente.
Parametrizando el sistema anterior nos queda que:
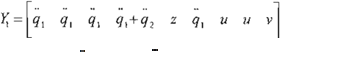 Y,
= [ ]
Y,
= [ ]
z
= 2cos(q1)q 1 +cos(q2 ) q2 - 2sen(q2 )q 1 q2
+sen(q2 )4 i u= gcos(q 1 )
v
= gcos(q1 + q2 )
Yi
=[o q1 +q2 O q1+q2 a O O O v]
a = cos(q
2
)q
1
+ sen(q2 )q;
|
e' = [01 82
|
83
|
94 e 96
|
|
el = 11
|
|
82 = 12
|
|
83 = m.Jc;
|
|
84 = m./ci
|
|
85 = Tni4Ls
8, :;:: m¡ü;
|
|
86 = rr;.fi2
e8 :;:: mi,
|
|
89 :::: fni lC2
|
|
|
|
|
87 es e9]
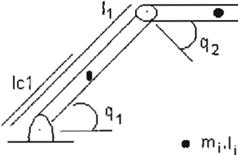 Fi
gura
1
.
Robot Mnlpulador rigldo
Fi
gura
1
.
Robot Mnlpulador rigldo
i=1,2
grados de libertad con artJculaclonos rotaelonállos.
 3 18
3 18


 Teniendo como valores de la estructura mecánica los siguientes:
Teniendo como valores de la estructura mecánica los siguientes:
11=0.9 Kgm2 m1=12 Kg. 11=0.53 m
lc1=0.33
12=0.25 Kgm2
m2=7 Kg 12=0.38 m lc2=0.16
/
\. ¡' 11'
\ (
g= 9.81m/s2
Se desea observar el seguimiento de una trayectoria dada por Qd1 = qd2 = 5*sen(t), para
ambas articulaciones, teniendo un tiempo de simulación de 4 seg.
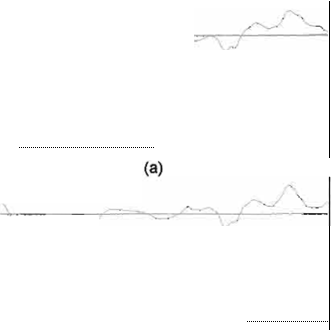
Podemos observar que en la figura 2(a} y
(b) el desempeño del control al seguimiento de la trayectoria deseada tanto en la articulación 1 como en la articulación 2, apreciando la convergencia
de las trayectorias en un tiempo considerablemente bueno.


'
.
 (a)
(a)
1 --
'
...-->
·
/
\
\
:l 1/
(b)
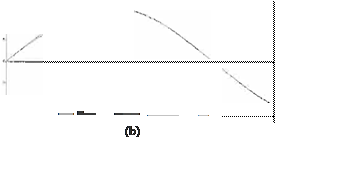
Ff
g.
3 Comportamior.
1
rror d
posición
d las articulaciones (a)1
y
(b) 2, b.ajo la
acción
del
controlador.
En ta figura 4(a) y (b) encontramos el comportamiento del controlador adaptable, el cual, inyecta gran cantidad de energía en los primeros instantes,
para después tener un comportamiento asintótico a cero, al alcanzar fa trayectoria deseada.
Figura 2. Comporl.J
.
1
..
de las
trayectorias de poste
Ión
d
;
u
tlculaciones
\a)
1
y
(b) 2,
bajo elcontrolador.
. '
 ...r -
...r -
--
 (a)
(a)
En la figura 3 (a) y (b} encontramos el error de seguimiento, el cual, como se puede observar, tiende a una vecindad muy cercana a cero, por lo que se
comprueba que el error de seguimiento tiende a cero para t oo.
 (b)
(b)
Fig.
4
Comportam1
,• J los torques do control para tas articulaciones (a) 1 y (b) 2, del manipulador.
 319
319
En la figura S(a), (b) y (e) se muestra la identificación de los parámetros e,. e2 y e6;
donde se puede apreciar que después de un cierto instante de tiempo, estos parámetros convergen a un valor acotado.
particular. garantiza la estabilidad asintótica del sistema en lazo cerrado.
REFERENCIAS
r7·'''\
r--',

:L_

 ......._. -··
......._. -··
-··----·----,--
(a)

(b)
..,...-..
l. Ortega R., Spong. Adaptive Motíon Control of Rígid Robots: a Tutoriaf. Automatica 25
(6), 1989, 877-888.
2. Desoer C, Vidyasagar M., Feedback Systems, lnput-Output Propíertíes. Academ ic Press
N.Y., 1975.
3. Lewis L. Control of robot Manipulators
MacMillan Publishing Co. N.Y., 1993.
4. Narendra K. Satble Adaptive Systems
Prentice Hall New Jersey, 1989.
 ...._ ·'
...._ ·'
(e)
Fig.
6 Estimación iJe 1 s parámetros (a)
01,
(b)
0
4
y
(e)
Oc delvoctor de parAmetros.
CONCLUSIONES
Además de los beneficios que se expresaron con anterioridad a lo largo del desarrollo, podemos recapitular la información y decir que este control resulta
bastante eficiente, pues permite mantener la estabilidad del sistema, ante incertidumbres dentro de los parámetros de la dinámica del manipulador; mas aún,
si r:1:0r la misma actividad de la tarea a realizar por Parte del manipulador se encontrara con variaciones en algún parámetro (ej. al cargar un objeto el
centro de masa del eslabón que contiene al punto terminal o la pinza cambia su valor} o en el caso de dinámicas no modeladas, permite el ajuste en línea
sin necesidad de rediseñar el controlador para elsistema.
Por otra parte observa la ventaja del diseño a partir delcriterio de Lyapunov, pues garantiza la estabilidad del sistema, y en este caso en
![]() C
ONTROL ADAPTABLE BASADO EN EL ANÁLISIS
oe
PASIVlDAD PARA UN ROB01
.
C
ONTROL ADAPTABLE BASADO EN EL ANÁLISIS
oe
PASIVlDAD PARA UN ROB01
.


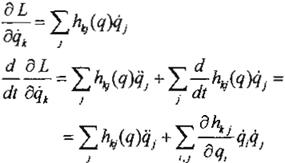 Entonces:
Entonces:
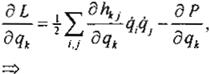
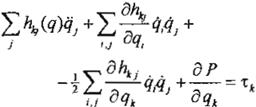 k= 1,...,n (Ec. 4)
k= 1,...,n (Ec. 4)
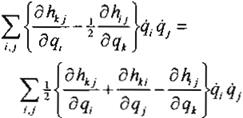 (Ec. 5)
(Ec. 5)


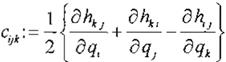


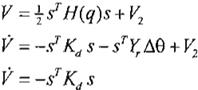

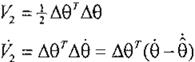
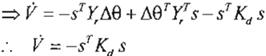

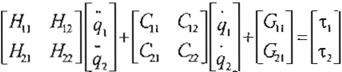
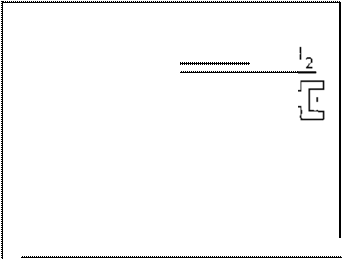 lc2
lc2
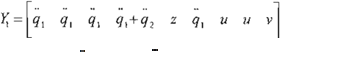 Y,
= [ ]
Y,
= [ ]
 Fi
gura
1
.
Robot Mnlpulador rigldo
Fi
gura
1
.
Robot Mnlpulador rigldo

 Teniendo como valores de la estructura mecánica los siguientes:
Teniendo como valores de la estructura mecánica los siguientes:

 (a)
(a)
 (b)
(b)


