COMPORTAMIENTO CAÓTICO EN REDES NEURONALES ARTIFICIALES

Hugo G. González-Hománó&z.; Marcos Montiol-Casbtllanos y Alejandro Corona.Jouanen Labor.atorto del Centro de lnvestJgación,Universidad L:i Sallo

RESUMEN

Las Redes Neuronales Artificiales (RNA) presentan comportamientos dinámicos complejos y, bajo ciertas circunstancias, presentan caos. En estos sistemas pueden presentarse toda clase de atractores: puntos de equilibrio, ciclos límite, atractores casi-periódicos y caos. Se han realizado muchos trabajos en lo que respecta a redes neuronales con retraso. Se ha demostrado que las redes neuronales con conexiones asimétricas y alta ganancia presentan también comportamiento caótico. En el presente trabajo se muestra un análisis de este tipo de RNA. Se muestra una RNA

de cuatro neuronas y se analizan las condiciones bajo las cuales presenta comportamiento caótico calculando los exponentes de Lyapunov.

ABSTRACT

Artificíal Neural Networks (ANN) present complex dynam1cs and, under certain circumstances, they present chaos. Al! kinds of attractors can be present in this systems, like equilibrium points, limit cycles, quasiperiodic and chaotic atractors. A lot of work has been done on neural networks with delay. lt has been proved that Neural networks with assymetric connections and high gain also present chaotic behavior. The current paper analyzes the behavior of this type of ANN. A four­ neuron ANN and the circumstances on which this system has chaotic behavior by cornputing the Lyapunov exponents is shown.

INTRODUCCIÓN Límite, el Casi-Periódico (Quasiperiódico} y por último, el Caótico.

Antes de entrar en materia, revisaremos algunos resultados de Dinámica de Sistemas, Teoría de Bifurcaciones y Caos y Redes Neuronales Artificiales.

Sistomas Dinám i cos

El estado de un sistema es el conjunto más pequeño de variables que determinan el comportamiento delsistema para todo tiempo.

El espacio de estado es un espacio n­ dimensional cuyos ejes coordenados son los estados de un sistema.

El atractor es el lugar geométrico descrito por la evolución en tiempo de un sistema en el espacio de estado en estado estable. Podemos clasificar el tipo de atractor por la geometria de éste distinguiendo el de Punto Fijo, el de Ciclo

Caos

Definición 1. Dado un mapeo x = f (x) , la evolución del sistema es caótica en un inteivalo 1 sí {3):

(i) Los puntos de f forman un conjunto

denso en l. (ii) f es transitivo.

(iii) f es sensible a condiciones iniciales.

De las caracteristicas del comportamiento caótico podemos resaltar la dimensión fractal del atractor, el mapa de Poincaré fractal, señal rica en frecuencias y exponente de Lyapunov positivo, siendo esta última una de las únicas medidas analíticas con las que se cuenta.

305

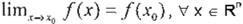
Figura 1.Funcíón de un nodo de

una RNA.

Figura 2. Diagrama del Circuito del

Nodo i.

Redes Neuronales Artfficiale IRNµ 1 las relaciones de voltaje en el circuito son:

Las RNA son sistemas dinámicos no Lineales, que pueden ser descritos por Ecuaciones Diferenciales Ordinarias (EDO), Ecuaciones en Diferencias (EeD) o Ecuaciones Diferenciales Parciales (EDP) (8). Un nodo efe una Red Neuronal puede esquematizarse como en la Figura 1.

donde:

-CV = JV +F(Vi)

F(V) = aSenh(bVi)

Los tipos de conexiones lntemeuronales (2) son: Acoplamiento Positivo, Acoplamiento Negativo, Desacoplado.

El Aprendizaje es la adaptación de los valores de los pesos de conexión para un fin especifico.

' e es la Capacitancia de

Retroalimentación.

J es la matriz de Pesos entre los Nodos i

y j.

= {

i = J

Jij

DESCRIPCIÓN DE LA RED

±cr

j "# j

La red que se propone permite los tres tipos de acoplamiento entre sus nodos. Implantaremos

Elvector V =

r

V1 V = (V, V2 ..· V0

con V1 como el

el modelo de esta red en un circuito electrónico. El circuito consiste en 4 amplificadores no lineales conectados entre sr. el esquemático de uno de los nodos se puede ver en ra Figura 2, los elementos pasivos son la resistencia y capacitancia de retroalimentación. La parte no lineal del circuito está compuesta por diodos.

Mod , _ _ 11(1

voltaje de salida en el nodo i.

a es una constante igual a 1.1125"10·1A.

b es una constante determinada por la siguiente relación.

b=gv-•

n

Se puede modelar el circuito considerando que cada amp-op tiene una corriente de entrada y un voltaje de offset de cero.

Simulación

El sistema de ecciones que describen la dinámica de la red fue simulado para diferentes

306

valores de pesos de la matriz J. Se encontraron atractores de punto fijo, de ciclo límite, cuasiperiódicos y caóticos. Se tomaron como constantes los valores de a y b, y fijas las

condiciones iniciales V1(0) = -1.5, V2(0) = V3(0)

= V(O) = O.

Punto fijo

Ciclo Limite

Para la matriz

0.333

--0.76

J =

--0.22

[-0.47

-0.28 -0.42

0.333 --01

0 -02 0.333

--0.02 -0.22

-0.93

-0..56]

--0.5

0.333

Los valores de J utilizados fueron:

0.6 Q.333 o

0 o.5.963l

0.333 --0.28

J "" -0;22 o

[

o

0333

-

--0.5

se obtuvo una órbita periódica como atractor,

en la Figura 5 se muestra la forma de onda en

tiempo.

0.47 o

022

Q.333

La Figura 6 muestra el atractor en una proyeccción del espacio de estado en el plano

La Figura 3 y la Figura 4 muestran el comportamiento dinámico del sistema, se puede observar que el atractor es un punto fijo.

Figura 3. Evolución de V2(t).

Figura 4.Proyecc16n V 1CV2).

V2 vs. V3 (con transitorios).

Figura 5. Evolución de V2(t).

Figura 6. Proyección V2(V3).

307

l

Atractor Quasiperiódíco

Se encontró la siguiente matriz para este tipo de atractor.

0.333 -0.35 -01 0.51

0.76 0.333 o -0.72

J =[ 0.83 -0.2 0.333 --0.45

-0.39 O 0.15 0.333

Caos

l

En este trabajo reportamos dos casos en los que se presenta comportamiento caótico, aunque pueden existir más.

A) Primer caso:

0.333 -0.2 -0.42 0.54

o

-0.76 0.333

0.78

La sef'\al en tiempo se muestra en la Figura

7. Observamos que esta señal está compuesta por varias frecuencias, .obteniéndose asi un atractor quasiperiódlco, mismo que se muestra en la Figura 8. Cabe aclarar que, aunque el sistema muestre varias frecuencias , el atractor sigue siendo un ciclo limite, independientemente que se le conozca como atractor quasiperiódico.

l= 0.83 -0.2 0.333 0.45

[

--0.05 o 0.17 0.333

Los exponentes de Lyapunov del sistema son

j, 1 = 0.03052, Ni= O. A.3 = -0.158, A4 = -0.60238 y

la dimensión de Lyapunov es DL= 2.19315

Observamos claramente que la dimensión del sistema es fractal y que los exponentes de Lyapunov son de Ja forma (+. O, -) que es una condición suficiente para que exista caos.

En la Figura 9 podemos observar el comportamiento en tiempo para esta matriz de pesos. En la Figura 1O se muestra una proyección del atractor que es de tipo Róssler.

Figura 7. Evolución de V 1 (t).

Figura 9. Evolución de V2(t).

Figura 8 . Proyección Vi(V,). Figura 10. Proyección V 1 (V 2 ).

308

B) Segundo caso:

0.333

--0.76

1 =

0.83

[

-0.07

-0.2 --0.42 0.54 l

0.333 --O.O1 O.78 --0.15 0.333 0.45

o 0.17 0.333

fundamentales del comportamiento caótico es su senslbllidad a condiciones iniciales, en la Figura 12 presentamos dos diferentes evoluciones en tiempo de la variable V1(t) para dos condiciones iniciales arbitrariamente cercanas. Podemos observar que las soluciones divergen mientras el tiempo aumenta.

obteniendo los siguientes exponentes de Lyapunov:

A.1= 0.0624

A. 2= o

A.3= -O.1427

A.¡= -0.5955

DL= 2.4373

En la Figura 11 se observa la respuesta en tiempo de variable V1(t).

Como se habla mencionado al principio del presente trabajo, una de las propiedades

Finalmente se puede observar en la Figura 13 una proyeccción del atractor en el plano V1 VS. V2.

Figura 11. E'lolución de V 1 (t).

Figura 12. Sensibilidad a

condiciones iniciales.

ANÁLI SIS DE RESULTADOS Y CONCLUSI ON ES

El estudio de redes neuronales involucra conceptos de dinámica no lineal, sistemas estocásticos (9) y algunos otros. Es importante conocer el comportamiento presente en una RNA, sus causas y las aplicaciones que éste pueda tener. Los resultados pueden ayudar a resolver aspectos fundamentales concernientes al comportamiento caótico dentro de las RNA de mayor orden (2,4,6).

La simulación computacional al Igual que la implementación electrónica son de gran ayuda para el estudio del comportam iento de las RNA (5). En este trabajo encontramos algunas de las configuraciones paramétr1cas en las que se presentan estos tipos de atractores. Se está trabajando para encontrar las condiciones paramétricas bajo las cuales un sistema como este presenta caos (8,1O). Es importante sei'lalar que es necesario realizar un análisis de estabilidad para este tipo de sistemas (T).

309