PROGRAMACIÓN DE UN ALGORITMO PARALELO PARA LA OBTENCIÓN DE TESTORES

,

Mario Farías-Elinos1 Patricia Ray6n-Villela2 y Manuel Lazo-Cortes3 1Laboratorio del Centro de Investigación, Universidad la Salle.

2sección de Control,Departamento de lngenieria Eléctrica, CINVESTAV-IPN.

31nstituto de Cibernética, Matemáticas y Fisica, la Habana, Cuba. e-mail:mfarias@sparcciulsa.ulsa.mN

RESUMEN

El presente trabajo muestra un programa que emplea técnicas de programación paralela. el cual permite realizar el cálculo de testores en un tiempo mucho menor que los algoritmos convencionales o seriados. Puesto que en este tipo de algoritmos se emplean cálculos con una complejidad exponencial, se consideran problemas NP completos (su solución se obtiene en un tiempo No Polinomial), característica que los hace aptos a ser resueltos aplicando 1écnicas de programación paralela.

ABSTRACT

The curren! paper shows a program which applies parallel programming techniques, which computes the typical test in less time than conventional or serial algorithms. This kind of problem is considered NP complete (problems which solve in Non Polynomial time) , that's why we used a parallel programming technique in order to solve it.

INTRODUCCIÓN

Un testor se puede definir como el conjunto mínimo de rasgos o variables con los cuales se puede distinguir un objeto de cualquier otro dentro de un problema de clasificación supervisada.

En un inicio se le conoció bajo el nombre de test (Prueba). término que fue introducido por Cheguis y Yablonskii en 1955 (1). en la ex Unión de Repúblicas Socialistas Soviéticas, quienes se dedicaron a realizar pruebas de interruptores eléctricos para detectar las fallas; posteriormente Zhuravliov (2) en 1965 dio una

fonnalización matemática, creando el término de Testor, lo que permitió considerar este concepto dentro del terreno de reconocimiento de patrones.

El problema de encontrar los testores puede ser comparable a dividir un número primo entre los valores positivos menores que él: es evidente que entre más grande sea el valor

primo. más tiempo se requerirá para dividirlo entre los valores positivos menores.

z

Para obtener la solución a este problema se requerirá de un tiempo exponencial , debido a que en el cálculo de testores, cada variable i existente implica tener que realizar cálculos adicionales, lo cual ocasiona que el algoritmo tenga una complejid ad O(t') y que el tiempo de solución se incremente en forma exponencial.

PROCESAMIENTO PARALELO

El procesamiento paralelo implica tener dos o más procesadores trabajando en forma conjunta sobre un mismo problema. de manera que sea posible la reducción de su tiempo de solución.

La técnica de programación paralela tiene dos objetivos principales:

447

1. Reducir el tiempo de procesamiento

utilizado por un algoritmo convencional.

2. Reducir la complejidad de un algoritmo.

El primero se cumple al momento de para lelizar . pero para el segundo se requieren técnicas de análisis de algorrtmos paralelos.

Para llevar a cabo la paralelización hay que tomar en cuenta varias limitaciones, una de las cuales es la independencia de datos; es decir, que en un momento determinado no se esté accesando la misma localidad de memoria en fonna simultánea, o bien, que no se dependa de un dato inmediato anterior.

Otro aspecto a considerar es la fonna en que se dividirá el problema; para ello es necesario conocer la forma en que se maneja la información.

Dentro del procesamiento paralelo existen dos paradigmas (3):

1. Homoparalelismo: Se refiere a dividir el trabajo realizado por un algoritmo en subtareas idénticas y de igual carga. las cuales se ejecutan en forma simultánea e

independiente (ver Figura 1).

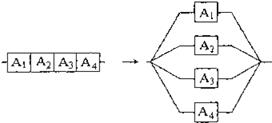
Figura 1.Homoparalelismo

2. Heteroparalelismo: Se refiere a dividir el trabajo realizado por un algoritmo en diferentes subtareas, pudiendo ser éstas de distinta carga, las cuales se ejecutan en forma simultánea e independiente (ver Figura 2).

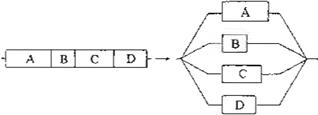
Figura 2. Heteroparalel smo

DESARROLLO

El algoritmo se programó en lenguaje e con librerías de PVM (Parallef Virtual Machine - Máquina Paralela Virtual) (4), sistema con el cual es posible comunicar varias computadoras UNIX y trabajar con su procesadores como si existiera una única computadora con varios

procesadores.

Los testores. y particularmente los testares típicos, son un útil instrumento para la selección de variables en un problema de clasificación supeNisada (5). Éste es un problema de complejidad exponencial , para el cual se han dado diferentes algoritmos que pretenden simplificar la búsqueda. Aún así, todos los algoritmos existentes hasta hoy son seriados y su eficiencia en algunos casos, para matrices de ciertas dimensiones deja mucho que desear. Es por eso que se desarrolló un algoritmo paralelo que disminuye los tiempos de cálculo; éste está basado en el algoritmo CC-difuso, descrito en 1980 (6) y que permite encontrar tanto los testores típicos clásicos como los difusos de Goldman.

La solución del problema se programó bajo el paradigma de homoparalelismo, el cual indica que cada procesador existente realiza el mismo trabajo; la diferencia es que cada procesador calcula diferentes testares, con lo que se logra reducir et tiempo de cómputo.

La idea, dentro del campo de reconocimiento de patrones, es encontrar las características mínimas necesarias para poder diferenciar un objeto de otro, por ejemplo :

Para reconocer un rostro podemos considerar las siguientes características;

• Tipo de ojos

• Color del ojo

448

• Tipo de ceja

• Tamaño de la boca

• Tamaño de los labios

• Tipo de nariz

• Color del pelo

• Forma del mentón

• Tamaño de la frente

Todas éstas son características que se toman en cuenta para poder diferenciar un rostro de otro, pero implica realizar comparaciones exhaustivas, y por lo tanto el proceso a nivel cómputo se hace lento e impráctico. Una forma de resolver este problema es encontrar un subconjunto que contenga un mínimo de características necesarias que permitan diferenciar un rostro de otro; a este subconjunto se le conoce como testor típico.

El cálculo de este subconjunto se lleva a cabo a través del una búsqueda exhaustiva, ya que se calculan todas las posibles combinaciones para fonnar al testar típico.

Estas características pueden agruparse en forma matrlcial de la siguiente manera:

donde:

O m representa un objeto.

Xn representa las características del objeto.

A esta matriz se le denomina matriz de Aprendizaje (MA).

A partir de la MA se realizan ciertos criterios de comparación, los cuales son diferentes para cada problema, y se obtiene la Matriz de Diferencias (MD), la cual nos indica qué tanto se asemeja un objeto a otro.

Posteriormente, de la MD se eliminan los renglones repetidos y se verifica si hay alguna super-fila. El criterio a utilizar será: utilizando dos renglones p y f cualquiera, se localiza el primer cero en p que aparezca en la misma

posición en t. si antes de éste se puede

encontrar en el renglón p un uno en la misma posición que en el renglón t un Qfil:Q, se dice que el renglón p es superfila del renglón t. Por ejemplo:

p = <11101> y t = <10001>

Se puede observar que en la posición 4 de ambos renglones se tiene un valor de cero y que antes de éste existen en la posición 2 y 3 un valor uno en p, y cero en t, lo que implica

que p es superfila de t. o bien, t es subfila de p.

Una vez que se realiza este proceso. se tiene como resultado una matriz denominada Matriz Básica o MB, con la cual podemos inicial el cálculo de testores con el algoritmo que se menciona más adelante.

Para que un subconjunto de características pueda ser considerada testor, no debe existir algún renglón que tenga valores de cero en las columnas de las características que formen el subconjunto.

El algoritmo utilizado es (7):

Para cada procesador existente:

Paso /: Se busca el siguiente valor diferen t e de cero disponible (Pivot e) e n l a i v JB .

Paso 2: Se agrega el Pivote a la li sta del cand idat o a testar; posteriorment e se verifica si el Pivote es un testor. y si lo es, se ai'tade a Ja li sta de testores y se salta al paso 5; de n o ser as/ se sigue al paso 3.

Paso 3: Se obtiene una li s ta de l os renglones causantes por los cuales e l Pivote no fue t estor y se inicializo a J el valor de ;.

Paso 4: Para elj-ésimo renglón causante:

Paso 4. /: Se busca el primer valor diferente de cero que sea compatible con los valores en la lista del dato a /estor; sí es compatible , se agrega a la lista de candidato y se salta al paso 4.2 .; de n o ser así , se salta al paso 4. 4.

Paso 4.2: Se verifica si el candidato es un /estor. Si es testor . se agrega a la lista de Les t o res y se brinca al paso 4 . 4 . de no ser así se busca en

449

J

\

.

< - "'

los renglones culpables a los nuevos culpables y se pasa enforma r ec ursiva al paso 4.

Paso 4.3: Se obtien e de la li s t o de candidatos el valor más reci ente y se brinca al paso 4.5.

Paso 4.4: Se busca en el j- és imo renglón otro valor diferente de cero y se brin c o al paso 4.2

Pa s o 4 . 5 : Se incrementa el va l o r d e j.

Paso 5: Se obtiene el sigui e nte J disponible en } 11/B

y se brinca al paso 2.

Los subpasos de 4 se realizan en forma recursiva, haciendo posible guardar la lista de renglones y pasar al siguiente renglón sin tener que volver a crear la lista.

Las únicas variables compartidas son: la que indica cuáles elsiguiente Pivote disponible y los apuntadores de la lista de testares. Para evitar los problemas de acceso simultáneo por parte de dos o más procesadores a dichas variables, la implementación del algoritmo se realiza a través de semáforos, evitando así caer en dead-lock o candado mortal.

En el momento de llevar a cabo la concatenació n de la lista se verifica que el nuevo testor aún no haya sido incluido: de ser así, se agrega , y de lo contrario, se desecha. Esto es con el fin de no tener testores repetidos, ya que este algoritmo encuentra todos Jos testores y sus permutaciones.

La idea de verificar si es testor se encuentra en la lista de renglones culpables, es evitar comparac iones innecesarias que incrementen

la complejidad, además de que se garantiza que únicamente se encontrarán nuevos culpables en los renglones ya culpables.

RESULTADOS

Se instaló el PVM (4) en 3 computadoras UNIX; en una SPARCstation-20, en una SPARCctassic (éstas dos con procesadores SuperSPARC v.8) y en una AlphaServer 4100 (con dos procesadores Alpha AXP); lo cual permite trabajar con 4 procesadores en paralelo.

Uno de los problemas en donde existen un gran número de características para llevar a cabo la clasificación de objetos fue la

identificación de diferentes herramientas de

trabajo, tales como: tijeras, cuchillos, trinches, palas, entro otras; las cuales son seleccionados para ser depositados en diferentes cajas. Este problema tiene 132 características en total las cuales al momento de rea lizar 'una comparación exhaustiva hacían que el proceso fuera lento y que en afgún momento dado se perdieran herramientas o que se cayeran de la banda de transportación.

La idea de introducir el término de testores es obtener un subconjunto con el mínimo de caracteristicas que permitan reducir el tiempo de comparació n y evitar que se pierdan objetos o que se caigan de la banda de transportación y por lo tanto, se agilice el proceso.

El segundo problema donde se utilizó esta técnica fue dentro del campo de la medicina, para detectar cuáles son los factores que intervienen en el problema de la lactancia a menores; este problema tiene una matriz con 60 características, las cuales para llevar a cabo una clasificación generaba un número muy grande de comparaciones. Aquí también se aplicó el uso de testores, con lo cual ffue posible simplificar el número de comparaciones y clasificar de una manera más rápida los factores que provocaron los problemas de lactancia .

Se pudo observar que eltiempo del cálcul.o de testores se redujo considerablemente en un 65% aproximadamente.

No. de variables	80486	SPARC v.8	PVM
60	168 hrs.	132 hrs.	86 hrs.
132	584 hrs.	456 hrs.	298 hrs.

CONCLUSIONES

Uno de los problemas que existen para el cálculo de testores, es que los algoritmos existentes hasta el momento trabajan bajo la

450