
 -
-
MORFOGÉNESIS UTILIZANDO REDES NEURONALES CELULARES
Alejandro Flores Méndez y Eduardo Gómez Ramírez Laboratorio delCentro deInvestigación, Universidad a Salle.
RESUMEN
Desde la antigüedad el hombre ha buscado entender el comportamiento de la naturaleza utilizando algoritmos o procedimientos matemáticos que simulen
características muy especificas de organismos biológicos. Ejemplos de ésto son el número áureo, el número omega, y características de tipo fractal,
dinámica caótica, autómatas celulares, etc.
Otro de los algoritmos que han demostrado gran capacidad para generar patrones biológicos son las redes neuronales celulares. En este trabajo se
presenta una breve introducción de varios algoritmos que se han utilizado en el proceso de generación de patrones biológicos y el procedimiento
necesario para morfogénesis utilizando redes neuronales celulares. Se presentan varios ejemplos descriptivos.
ABSTRACT
Since ancient times the human being has tried to understand the behavior of the nature using algorithms or mathematical procedures that simulate very
specific characteristics of biological organisms. Sorne examples are the golden ratio, the omega number, and fractal characteristics, chaotic dynamics.
cellular automata. and so far.
Another algorithms that show great capacity for generating biological patterns are Cellular Neural Networks (CNN). In this work we present a brief
introduction of several algorithms used in the process of making biological patterns and the necessary steps for achieving morphogenesís using CNN.
Sorne descriptive examples are presented in this work.
INTRODUCCIÓN
La historia matemática de la simulación y entendimiento de procesos biológicos se remonta a la época de los griegos con el número áureo y han existido
diferentes aproximaciones hasta nuestros días. Las concepciones de la naturaleza se han modificado y ha sido tal el desarrollo que en los últimos años
se ha estado utilizando el término de Nueva Ffsica al reciente enfoque para describir estos problemas. En este artículo se han seleccionado
algunos de los temas más trascendentes para la explicación de la naturaleza, específicamente en la formación de patrones biológicos. Se inicia con la
proporción áurea y algunos comportamientios numéricos interesantes, posteriormente se analizan algunos tipos de fractales; en la siguiente
sección se muestra la simulación de un sistema físico con automátas celulares y, por último se presentan algunos ejemplos utilizando un algoritmo de
reciente creación: las Redes Neuronales Celulares (1), (2).
NÚMERO ÁUREO
Uno de los primeros intentos por entender y simular el comportamiento de la naturaleza, fue el número áureo (3). (4). El número áureo fue definido por
el arquitecto romano Marco Lucio Vitrovio Polión en el siglo 1 d.C. de la siguiente forma:
Definición 1:
Se propone un segmento AB que tenga una longitud unitaria, sea e el punto de división:
 423
423

|
A
|
|
|
e
l
|
|
B
|
la prolongación de la base del cuadrado. Así el rectángulo tendrá como dimensiones un largo
|
|
|
|
|
1
|
|
|
igual a la suma de la diagonal mencionada con
|
|
|
|
1
|
|
|
|
la mitad de lado del cuadrado y, por ancho la medida del lado del cuadrado. Si se emplea el
|
|
|
|
|
|
|
|
teorema de Pitágoras, se puede demostrar que
|
|
|
X
|
|
!
|
1-x
|
|
la razón entre la altura (ancho) y la base (largo)
|
 donde
:
donde
:
longffud AB
= 1
parte mayor =
AC
= x parte menor = ca = 1-x
De aquf
se establece la siguiente proporción
parte
menor parte mayor
'--------:::;: . ---
parte mayor toda la recta
}
-
X
X
del rectángulo es la razón áurea. Una vez
construido el rectángulo áureo podemos descomponerlo en un cuadrado y en un rectángulo áureo menor, al cual podemos dividir de la misma forma , y así indefinidamente . Apoyados en el vértice de cada cuadrado trazamos un cuarto de circunferencia de radio coincidente con el lado
del cuadrado de tal manera que todos los trazos se enlacen para formar una sola curva que se conoce como espiral de Arquímídes. o espiral áurea (Fig.
2).
Esta espiral se presenta en los cuernos. garras y colmillos de algunos animales, como
-- = -
X
Í
(Ec. 1)
es el caso de la cabra montañesa o los borregos cimarrones. y en otros de formas
con
lo cual se obtiene la
ecuación
x
2
+ x - J :::: O , cuyas ralees son X 1 = 0.6180 X z :: -}_6 / 80 .
La primera ralz
se
define
como
número
áureo
y Ja segunda (en valor absoluto) a su inverso.
Este número tiene un comportamiento algebraico muy interesante, la parte decimal del número áureo y de su inverso son exactamente la misma.
Desde esta época se encontró que este número aparecía en diferentes situaciones en la naturaleza y las matemáticas. Algunos ejemplos han sido descritos
en y se muestran a continuación.
El
rectángulo
áureo
.
El rectángulo áureo (Fig. 1), base de construcción de todas las figuras armoniosas, está sustentado en un cuadrado cualquiera en el que se toma el
punto medio de lados opuestos. Al unir estos puntos medios se forman dos rectángulos idénticos. A uno de ellos se le traza una diagonal, a partir de la
cual se dibuja un segmento de circunferencia hasta
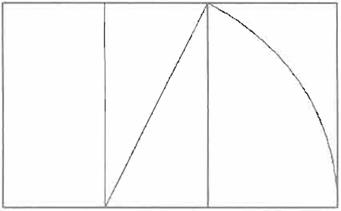
Figura 1. Rectángulo Áureo.
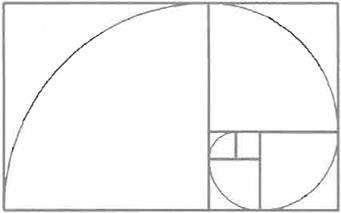
Figura 2. Espiral Áurea.
 424
424

largas con menor curvatura como en el caso de los colmillos de los elefantes y en la concha del nautilus (5).
La estrella pitagórica
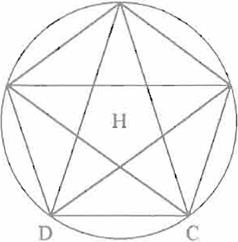
Es una estrella regular de cinco puntas. inscrita en un pentágono regular ABCDE equilátero y equiángulo (Fig. 3). Se le dio el nombre de estrella
pitagórica ya que se cree que esta figura cautivó a la secta de los pitagóricos por sus propiedades geométricas y decidieron elegirla como un símbolo
distintivo de la hermandad. Como en el corazón de la estrella pitagórica se encuentra otro pentágono regular, resulta posible la construcción de una
sucesión anidada de estrellas pitagóricas concéntricas
A
E
 B
B
Figura 3. Estrella pitagórica.
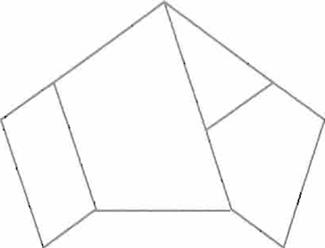
Figura 4. Nudo Áureo
.
que. por pares, estén colocadas en forma invertida . Este pentágono puede ser elaborado con una tira de papel haciendo un nudo sencillo y aplanando
cuidadosamente. A este mecanismo se puede referir como la creación de un nudo áureo, donde los dobleces muestran a las diagonales sucesivas cortándose
en extrema y media razón (Fig. 4).
Este comportamiento se ha encontrado en los números de Fibonacci, en la disposición de las hojas en el tallo de una planta. en los botones o centros de
algunas flores, como los girasoles y las margaritas y en varios sólidos como el dodecaedro y el icosaedro, por
mencionar algunos . Muchos escritores. artistas y arquitectos han dedicado obras o de alguna forma asignado proporciones.
Existen otros sistemas en los cuales se ha encontrado bajo ciertas características como son: el comportamiento dinámico de sistemas mecánicos y la
mecánica de suelos (6).
A pesar de que durante mucho tiempo se sostuvo y se buscó si el número áureo formaba parte del comportamiento de la naturaleza, en las últimas
décadas se han encontrado otras formas de describir el comportamiento de otros patrones biológicos, como son los fractales.
FRACTALES
Los trabajos de Mandelbrot que describían la existencia de cierta geometría en la Naturaleza, determinaron una nueva forma de ver las formas y
estructuras de varios organismos. Ejemplos de esto son la estructura de nubes y arrecifes. patrones de piel y estructuras simples que se autoorganizan
para formar estructuras más complicadas (estructuras fractales), turbulencias y dinámicas que se les denominaba casi aleatorias, y en
las cuales e ha encontrado un cierto tipo de orden.
A partir de estos trabajos ha habido una gran cantidad de desarrollos y herramientas utilizando la idea de fractalidad. Es decir, es más sencillo
almacenar la regla local que genera el patrón, que almacenarlo todo. Esta idea ha sido una herramienta muy útil en la compresión y procesamiento de
imágenes.
Esta idea de fractalidad ha sido también muy utilizada para la generación de patrones
 425
425

biológicos. En la siguiente sección se hace una pequeña descripción de esto en relación con la evolución de plantas.
FRACTALES EN LA EVOLUCIÓN DE LAS PLANTAS
La idea de geometría fractal ha dado una nueva herramienta a los biólogos para modelar la compleja dinámica que exíste entre los organismos y su medio
para poder probar sus hipótesis sobre la evolución y su comportamiento. Una de las áreas donde la computadora se ha utilizado como herramienta para
probar estas hipótesis es en la evolución de las plantas (Fig. 5). Esta idea se basa en que la evolución es manipulada por la necesidad de la planta
para minimizar los mecanismos requeridos en el aprovechamiento de la luz solar en un crecimiento vertical. Existen otras hipótesis con respecto a la
forma en que se reproducen y como colocar sus semilllas, o polen (7).
Estas ideas se combinan con ciertos valores de probabilidad para generar la diversidad biológica.

Figura 5. Planta obtenida mediante reglas fractales.
Las simulaciones que se obtienen son verificadas utilizando el registro de fósiles. Cabe hRcer notar que la verificación no implica una comprobación,
sólo un camino para entender las formas generadas por la naturaleza.
AUTÓMATAS CELULARES
La idea de autómatas celulares (AC) fue presentada por Von Neuman hacia finales de los cuarenta (8), y actualmente es un paradigma de la computación
paralela.
Los AC se definen como un arreglo de celdas que cumplen principamente con tres características :
o son homogéneas (las celdas utilizan la misma regla),
o emplean reglas locales (sólo interactúan con sus 'vecinos'; ver Fig. 6), y
o son paralelas (el nuevo estado de todas las celdas se calcula a un mismo tiempo).
Existen aplicaciones de AC (9) en diversas áreas tales como:
o simulación de la conducción del calor en un fluído,
o simulación de la respuesta inmune,
·
::>
simulación de la turbulencia química,
o procesamiento de imágenes,
o teoría de la computación,
» simulación de procesos de morfogénesis (ver Fig. 8), etc.;

a) b)
Figura 6. Vecinos de una celda (central) compuestos por a) ocho vecinos (convencional u ocho conectado) y b) por cuatro vecinos (vecindad de
Laplace).

 426
426
Un ejemplo de AC para la simulación de las moléculas de agua dentro de una tetera se muestra en la Fig. 7; las reglas de los AC son reglas lógicas,
como la que permite la simulación de la tetera; la dinámica de ésta se obtiene mediante las siguientes condiciones:
si espnred
la
c
elda
no
cambia
sino
c
alcula
el
número de
colision
es
c
alcula
lasparedes que ha
y
a
lr
e
d
edo
r
si
hay
pared
rebota
sino
si rebota
contra una
partí
c
ula
c
ambia
su
dirección
al s
en
tid
o
op
uesto
si
no
(no
hay nada en su
camino)
co
ntinúa en
la misma dir
ección
fin
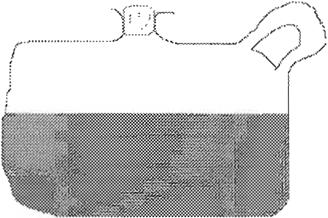
a)
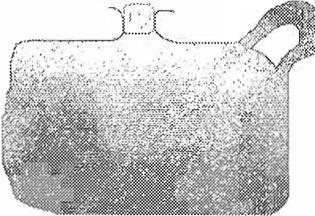
b)
Figura 7. Modelado de la distribución de partículas en un recipiente mediante un AC. La figura a) muestra las condiciones iniciales mientras que la
figura b) indica como evoluciona el sistema.
Otro ejemplo de Ja utilización de los AC se puede observar en la Fig. 8 la cual muestra la evolución de un espacio con una entrada aleatoria
hasta la eventual formación de patrones que describen la piel de algunos seres vivos . Además de mostrar una extraordinaria semejanza con los patrones
que se pueden observar en condiciones naturales es también empleada como base en teoría de la evolución. En la Fig. 8 los patrones que se observan de
izquierda a derecha además de ser pasos subsecuentes en el AC también lo son en la evolución de los seres vivos ya que la segunda imagen de izquierda a
derecha se observa en peces, la siguiente en anfibios y finalmente la figura de la derecha es fácilmente asociada con las pieles de los felinos, ej.:
leopardos.
En general un autómata celular puede realizar cualquier tarea capaz de definirse mediante reglas lógicas siempre y cuando su estructura sea regular.
REDES NEURONALES CELULARES
Las Redes Neurona les Celulares (RNC) son un tema que actualmente ha sido muy estudiado debido a su capacidad para el procesamiento de imágenes, la
facilidad con que se puede aplicar en circuitos eléctricos y la pequeña cantidad de parámetros que se deben determinar (para la mayorfa de las
aplicaciones basta con 19 parámetros) la cual no varía con las dimensiones del espacio que se analice.





Figura 8. Evolución de un AC donde se puede observar una eventual agrupación de los elementos en el sistema hasta que
se llega a encontrar un patrón bien definido
(imagen de la extrema derecha), el cual se observa en las pieles de ciertos mamíferos.
 427
427

Las RNC fueron creadas en 1987 por el Profesor Leon O. Chua y para 1990, gracias a una muy buena aceptación por parte de la comunidad científica, se le
dedicó un congreso bianual (Congreso Internacional de RNC y
sus
Aplicaciones
)
que recoge los trabajos
realizados tanto en desarrollos a nivel teórico así como los avances obtenidos en diferentes aplicaciones tales como: procesamiento de
imágenes (1O), simulación de modelos complejos en biología (11), sistemas no lineales, etc.. encriptación de datos (12). realización de RNC en
circuitos y computadoras (13), (14), etc.
La base de las RNC se sustenta fundamentalmente en dos pilares: las Redes Neuronales Artificiales (RNA) y los Autómatas Celulares (AC).
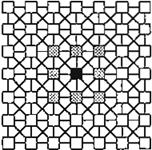

a) b)
Figura 9. Diferentes tipos de vecindades dependientes del valor de r. La figura a) muestra la vecindad de una celda (denotada por el color
negro) en el cual r
= 1.Nótese que la distancia máxima
entrela celda central y sus vecinas (celdas grises) no es mayor que 1.La figura b) hace referencia a una vecindad donde r = 2.
Básicamente una RNC puede ser descrita como arreglos n-dimensionales de elementos simples llamados celdas (unidad básica de una RNC) cuya dinámica es no lineal y que trabaja mediantes reglas de nivel local.
El nivel local se refiere a que la regla hace
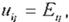 Ecuación de entrada:
Ecuación de entrada:
(Ec. 5)
 428
428
uso de· una vecindad finita definida por la siguiente ecuación:
Nr(i.J )
= fC(k.I) mC1x{l k -1¡,¡1-JI} r,¡ (Ec. 2)
l l k -5. M ;/ s l s N
Ejemplos de diferentes tipos de vecindad se pueden observar en la Fig. 9 la cual muestra una vecindad para r= 1 (a) y r = 2 (b)
La dinámica de una RNC se obtiene mediante el siguiente conjunto de ecuaciones:
Ecuación de estado:
dx,
¡(
t
}
= -xu{ t) +¿""""' A(1...1·..k.l)Y1r1( t )
di
C
f
k
J
J.N,(
1
J)
(EC. 3)
+ "'L,8( 1,j ;k .l )u"' + 1
C(tJ)tJl,(1J)
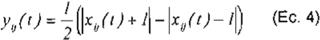 Ecuación de salida:
Ecuación de salida:
Existen algunos otros modelos para los cuales se puede emplear una extensión de una RNC la cual hace uso de más de una capa. éste se conoce como RNC
multicapa, pero para su mayor estudio al respecto se sugiere la lectura de (1) y (15).
MORFOGÉNESIS UTlUZANOO REDES
NEURONALES CELULARES
El término morfogénesis se emplea para referirse al desarrollo evolutivo de la estructura de un organismo o parte. En cuanto al modelado de
sistemas biológicos se han hecho ya algunos trabajos en RNC (10), (16).
Una de las principales áreas de interés se encuentran en los modelos que describen la formación de patrones observados en algunos mamíferos,
particulannente en las pieles de algunos felinos, esto debido a que en el caso particular del leopardo o el jaguar se presentan característ icas que
son interesantes en cuanto a los diversos comportamientos que se observan .

Uno de los modelos más aceptados en la actualidad para lo que es el modelado de patrones biológicos es el de reacción-difusión, también conocido como
el sistema Gierer Meinhardt (17) descrito por:
o
A
mismo comportamiento se puede obtener cuando se varían los parámetros en función del espacio, sin embargo , esto no es tan plausible puesto que sería
equivalente biológicamente a decir que sólo algunas porciones del cuerpo se verían afectadas por algún fenómeno externo.
Para el caso general de una RNC los
-a == F( A,B)+ D/v 1A
==
G(
A,
B
)+
D/v
1
B
(Ec. 6)
parámetros son invariantes en el espacio y el tiempo, sin embargo. se pueden exhibir distintos comportamientos por el hecho de que la estructura que se
está analizando no es igual en todas sus porciones; esto es, regresando al ejemplo de la cola, que el diámetro de ésta se
Para la ecuación 6 A y 8 son concentraciones químicas de los llamados
activador e inhibidor respectivamente, FO y
GO son funciones no lineales y DA y De son los coeficientes de difusión. De éstos, el activador crea la inestabilidad que permite la formación de patrones,
mientras que el inhibidor aporta la estabilidad al sistema una vez que el patrón ha sido creado. Ambos qufmicos se difunden a través del espacio, pero si
se ha de estabilizar el sistema es necesario que el inhibidor se difunda mucho más rápido que el activador (DA »De).
reduce conforme se acerca al extremo final.
Así que se considera que el espacio que se está analizando tiene una geometría como la de una cola. la cual reduce su diámetro según se acerca a la
punta y se emplea una RNC cuya regla está dada por las siguientes mascarillas:
 1-
0
.25
-
1
-
J
.
5
-/ -0.25
1-
0
.25
-
1
-
J
.
5
-/ -0.25
2.5
7 2.5 -J
El modelo de Gierer-Meinhardt se puede
A =
15
7 -23.25 7 -1.5 (Ec. 7)
llevar a cabo en una RNC mediante una simple consideración; puesto que el modelo es una ecuación de segundo orden y las RNC son sólo de primer orden,se
deben obtener los valores de las mascarillas de manera que permitan tanto la inhibición como la excitación. Esto se consigue a través de un aumento en
el tamaño de la vecindad,con lo que se puede dar valores positivos a las celdas contiguas a la que se está analizando, lo que permite su excitación,
mientras que se le inhibe con los vecinos que estén a una distancia de dos celdas. Es gracias a esto que se obtiene la interacción de los dos elementos
necesarios para la aparición de formas buscadas.
Como ya fue mencionado, algunos de Jos patrones más interesantes se presentan en las pieles de los felinos y, en particular en los leopardos, puesto
que presentan diferentes comportamientos . Esto debido a que son "sensibles" a la estructura del cuerpo que se analiza . En otras palabras cuando uno
observa la cola de un felino comúnmente puede obseNar manchas en uno de los extremos de la cola, mientras que en la parte terminal de
ésta las manchas pasan a ser anillos. Este
-
!
2
.
5
7
2.
5
-
!
-
0.25
-
J
-
1.5
-
!
-
0.25
B
=
0.
l
= -0.7
Como condición inicial se da a la RNC valores aleatorios de entrada con una distribución uniforme entre -0.1 y 0.1 (Fig. 1O.a).
/X(O)/
<= O. 1 (Ec. 8)
En realidad ésta no es una restricción muy fuerte ya que en la naturaleza es común observar en el momento del nacimiento cómo un ser tiene
aproximadamente el mismo color para la mayor parte de su cuerpo.
Además considerando esta entrada aleatoria se podrán obtener una infinidad de patrones,
inclusive en presencia de pequeñas variaciones (compare las Fig. 1o.b y 1O.e), pero éstos
continuarán presentando el mismo comportamiento que es precisamente !o que se
 429
429


a)

b)

Figura 10. a) Entrada a una RNC para el modelado de la cola de unleopardo. Los valores presentados tienen una distribución uniforme con
valores entre -0.1 y 0.1.
b)
resultado de una RNC empleando (7); nótese como a pesar de que se utiliza una misma regla para todas las celdas se pueden distinguir varios
comportamientos gracias a que la estructura del cuerpo no es la misma para todas sus porciones.
distingue del análisis visual de las pieles de los felinos.
Sí bien la entrada mostrada en la Fig. 1O.a se ve como un área rectangular, en realidad la porción con la que se trabaja de ésta no es
todo, sino que se emplean 7 RNC conectados entre sí cuyas dimensiones son M = 20 y N =
{20, 18, 16, 14, 12, 1o, 8}. La salida obtenida utilizando la ecuación 7 se puede observar en
la Fig. 10.b aquf el comportamiento de la RNC se ve afectado debido a que las dimensiones no son iguales, por lo que en un extremo se distinguen
manchas mientras que en la punta se ven anillos. Esto se debe a que son
·sensibles", como ya se mencionó anteriormente,a la estructura del cuerpo que se analiza (manchas en uno de los extremos de la cola y anillos en la
parte terminal de ésta). Además si se da una nueva entrada a la red con las mismas características se obtiene un patrón completamente diferente corno
se puede observar en la Fig. 1O .e.
CONCLUSIONES
El esfuerzo del hombre por imitar el comportamiento de la naturaleza le ha permitido desarrollar una gran cantidad de herramientas matemáticas. Como se
puede observar los modelos que mayor impacto han tenido, son aquéllos que están definidos por reglas locales y no por un modelo matemático global. A
pesar de la potencialidad que han demostrado, todavía no existen algoritmos generales para obtener comportamientos globales a partir de reglas locales.
aunque los resultados presentados muestran un gran avance en este camino.
Las RNC permiten con tan sólo el empleo de reglas locales y a partir de condiciones que se considerarian en otro caso como ruido, la
obtención de modelos sumamente complejos que en esle caso permiten la simulación de
seres vivos gracias a la ínteracción de los valores de sus vecinos. Con esto se consigue
 430
430

una cierta forma de agrupación, la cual visualmente puede ser interpretada como patrones.
Se puede concluir además que un sistema local no tiene por qué comportarse forzosamen te de manera similar en todas las porciones de Ja estructura que
se está analizando, esto es claro tras la simple observación de los resultados ofrecidos .
Las RNC son, pues. una nueva alternativa además de los métodos ya existentes que tratan de alguna manera de descifrar los procesos que describen el
origen de la vida y las formas que ésta presenta. ofreciendo así una nueva perspectiva para admirar lo maravilloso que es todo lo que nos rodea a pesar
de lo simple que pueden ser las reglas que lo originan.
REFERENCIAS
Chua L. O. y Yang L., Cellular neural networks: theory, IEEE Trans. Circuits and Systems, CAS-35, 1257-1272 (1988).
2 Chua L. O. y Yang L.. Cellular neural networks: applications, IEEE Trans. Circuits and Systems, CAS-35 , 1273-1290 (1988).
3. Berumen G. E., Proporción áurea, Mafhematica, boletín del Departamento de Matemáticas la
Escuela de Ingeniería de la Universidad la Salle, Enero 1996.
4. Berumen G. E., Proporción áurea, Mathematica, boletín del Departamento de Matemáticas la
Escuela de Ingeniería de la Universidad la Salle, Febrero 1996.
5. Ghyka M., The geometry of art and /ife ,
Dover, 1977.
6. Cuevas Barajas L.. La proporción áurea en la naturaleza. Investigación, Revista de Divulgación de Investigación en ULSA, diciembre 1990.
7. Niklas. K. J., Computer-simulated Plant Evo!ution. Scientific American, marzo 1986.
8. von Neumman J.. Theory of Self- reproducing Automata, (editado y complementado por A. W. Burks). University of
lllinois Press, 1966.
9. Toffoli T. y Margolus N. Ce/fular Automata Machines, The MIT Press, Cambridge. Massachussetts , 1987.
10. Crounse K. R. y Chua L. O., Methods for lmage Processing and Pattern Formation in Cellular Neural Networks, IEEE Transactions on Circuits and
Systems-1, 42 (i0):583-601, Octubre 1995.
11. Ogorzalek M. J .. Z. Galias, A. Dabrowski y
W. Dabrowski, "CNN with Chaotic Elements for Modelling Biological Functions", Proc. IEEE CNNA-96 , pp. 279- 284, 1996.
12. Caponetto R., Lavorgna M. & Occhipinti L., "Cellular Neural Networks in Secure Transmission Applications", Proc. IEEE CNNA-96, pp. 445-450,
1996.
13. Gómez Ramírez E., Ramos Viterbo V., Alencastre Miranda M., Flores Méndez A. y Sánchez de Tagfe A., "lmplementation of a Cellular Neural Network
over an Optical Computer", Proc. IEEE CNNA-96 , pp. 445- 450, 1996.
14. O'Sullivan G., Horan P.. Hegarty J..
Kakízaki s.. Kelly B. y McCabe E., "A Fully
Optically Addressable Connected Component Detector in CMOS", Proc. IEEE CNNA-96, pp. 445-450, 1996.
15. Kozek T., Roska T. & Chua L. o.. Genetic algorithm for CNN template learning, IEEE Trans. Circuits and Systems, CAS-40, 1993.
16. Setti G. & Thiran P., "Biological Pattem Formation with Cellular Neural Networks", Proc. IEEE CNNA-96, pp. 279-284, 1996.
17. Meíndhart H., Models of Biological Pattem Formation, Academic Press, Londres, 1982.

![]() -
-

 donde
:
donde
:



 B
B


















