ANÁLISIS ESTRUCTURAL, CINEMÁTICO Y DINÁMICO DE UN ROBOT MÓVIL EXPERIMENTAL
Hugo G. González Hernández, Bernardo Tame Rivera y Eduardo R. Mondragón Parra
Laboratorio del Centro de Investigación,Universidad La Salle
RESUMEN
En el presente trabajo se muestra un análisis detallado de la dinámica de un robot móvil. Se presenta primeramente un análisis estructural y,
posteriormente, el análisis cinemático y dinámico del sistema, por último se muestran algunas simulaciones del comportamiento dinámico. El robot consta
de dos motores: uno de tracción y otro de dirección. El robot puede moverse en cualquier dirección en el plano horizontal.
ABSTRACT
The current paper shows a detailed analysis of an experimental mobile robot dynamics. First, an structural ana lysis and then a kinematics and dynam\cs
analysis are shown, finally we show sorne simulations of its dynamical behavior. The robot has two de motors: a traction motor and a direction motor.
The robot can move in any direction on the horizontal plane.
INTRODUCCIÓN
 Un robot móvil omnidireccional permite el seguimiento (1) de diferentes tipos de trayectorias de manera fidedigna. En el presente trabajo se muestra un
análisis detallado del comportamiento estructural, cinemático y dinámico de un robot móvil omnidireccional. El robot que se analiza es el segundo
prototipo de la serie RoMEO (Robot móvil experimental ominidireccional).
Un robot móvil omnidireccional permite el seguimiento (1) de diferentes tipos de trayectorias de manera fidedigna. En el presente trabajo se muestra un
análisis detallado del comportamiento estructural, cinemático y dinámico de un robot móvil omnidireccional. El robot que se analiza es el segundo
prototipo de la serie RoMEO (Robot móvil experimental ominidireccional).
ANÁLISIS ESTRUCTURAL
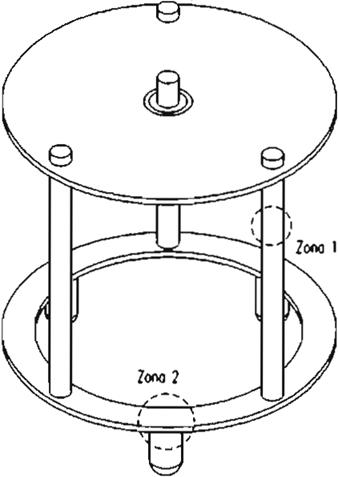
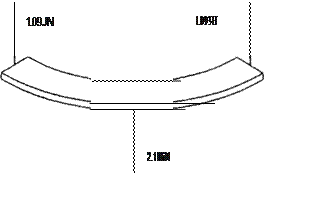
En la Fig. 1 se muestran dos de las zonas más representativas del análisis estructura!.
Análisis de la Zona 1.
Este análisis resulta ser bastante sencillo, ya que se considera la carga aplicada al poste como axial, además de estática (2).
La carga total de los tres postes se muestra en la tabla 1.
Figura 1.Estructura de mini-RoMEO.
 433
433

Tabla 1.Carga total.
|
Elemento
|
Masa en Q
|
|
Base
|
380
|
|
Tomillos
|
(3)(6) = 18
|
|
Motor
|
170.5
|
|
Circuito
|
100
|
|
Total
|
668.5
|
La carga total es de 6.558N. La carga de un solo poste es (por simetría): Wposte = 2.186 N. El área del poste es:
Aposte = 0.25p(O.D115 m)2 ::: 1.039E - 04 m2
los valores de resistencia del aluminio comercial son:

l 1105MPa 1 41]>Pa l 12 Pa 1 48sMa
calculando el esfuerzo de trabajo y
comparándolo con el esfuerzo de fluencia:
St = 2.166N/1.039 E-04 m'= 21.04 kPa
de tal forma que la estructura es suficientemente robusta.
Anál i sis de la Zona
2
.
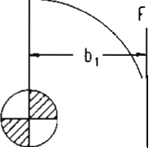
Para este análisis se considera la sección mostrada en la Fig 2.
Las cargas de 1.093 N son de los postes, mientras que la reacción de 2.186 N es del
rodamiento. Para considerar esta parte en equilibrio estático es necesario considerar un momento en sentido contrario al generado por las dos cargas de
1.093 N. Las distancias de aplicación de fuerzas se obtuvieron mediante el modelo representado en la Fig 3.
Para r = 0.09 m y ang = p/6: conociendo
Y = ((0.09)(6)sen(p/6))/p Y = 0.0859 m;
r-Y = 4.056E-03 m;
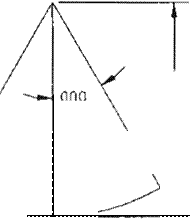 X = 0.005 m; 2X ::: 0.01 rn.
X = 0.005 m; 2X ::: 0.01 rn.
ong y
 l
l
(
- y
Figura 3. Distancias de aplicación de
fuerzas.
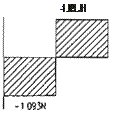
Con estas distancias conocidas podemos obtener los diagramas de esfuerzos cortantes y momentos, los cuales se muestran en la Fig 4.
 V
V
 11
11
Figura 2.Cargas actuantes en la zona 2.
-5.46Sí-03 N-m
Figura 4. Diagramas de esfuerzos cortantes y momentos.
 434
434
El esfuerzo normal es:
Me
cr = - -102.47 kPa
1
s = -102.47kPa
ls1I "' (y 1)(r) = Jx + Y
S1COS01= X1
s1sene ,= Y1
donde O :5: q1 < 360° y -a < g 1 < a
(Ec. 1)
(Ec. 2)
(Ec. 3)
<
..:
,).
El esfuerzo cortante es:
De las ecuaciones (1), (2) y (3) se obtiene:
'tmáx = T/Q; Q = bh2/(3+1.8(h/b))
Tmax = 46.55 kPa
x, =(y 1J(r)cose 1
y 1 = (y 1)(r)sen01
(Ec. 4)
(Ec. 5)
Analizando mediante el círculo de Mohr encontramos.
S1 = 46.55 kPa + 102.47 kPa/2 = 97.785 kPa
ANÁLISIS CINEMÁTICO
En el caso del análisis cinemático directo tenemos como variables independientes a e
donde (4) y (5) son las ecuaciones de la
cinemática directa.
La ecuaciones de cinemática inversa son:
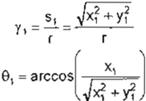 (Ec. 6)
(Ec. 6)
{Ec. 7)
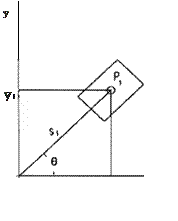
El caso general para encontrar la ubicación del centroide del robot:
(ángulo del motor de dirección) y y {ángulo del motor de tracción). Como variables dependientes a x , y . Como parámetro a r.
Xn.1 = Xn + (fo..1 - Y11)(r)cos{0n)
Yn.1 = Yn + (Yn .1 - r)(r)sen(0n)
(Ec. 8)
(Ec. 9)
1 1
Véase la Fig 5.
La consigna de posición es el punto P1(x ,y) 2
Se considera que no hay deslizamientos y que inicialmente el eje de la rueda está alineado con el eje X.
)( 1
Figura 5. Esquema cinemático.
para un punto Pn. n = 1,2,3,...
ANÁLISIS DINÁMICO
Se considera que el centro de masa está sobre el vástago, el robot requiere balanceo para cumplir esta consideración. Véase la Fig 6.
 r
r
 01
01
 r p
r p

Figura 6. Diagrama de cuerpo libre.
 435
435
Por suma de fuerzas P = 3F
por suma de momentos
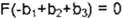
por lo que
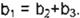
 Lo anterior se cumple, apoyado en un análisis geométrico. En a,, a , a , hay una
Lo anterior se cumple, apoyado en un análisis geométrico. En a,, a , a , hay una
Se consideraron las variables y parámetros de la Tabla 2:
Tabla 2. Variables y parámetros
2 3
misma fuerza de fricción F, dado que el peso
es distribuido entre los tres apoyos de manera uniforme. Además. son rodamientos del mismo tipo. Véase la Fig 7.
 Las ecuaciones de Lagrange son:
Las ecuaciones de Lagrange son:
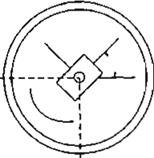
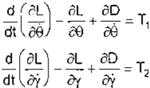 y (Ec. 10)
y (Ec. 10)
(Ec. 11)
y
La energía potencial es nula. La energía cinética es:
X T = 1 .v2-- + 1 a·2 + 1 ·i2
(Ec. 12)
Figura 7.Esquema dinámico.
con
2 2 1 2 71
Véase además la Fig 8.


 V
V

Figura 8. Rueda de tracción.
v =(rJ(r) (Ec. 13)
el Lagrangiano será
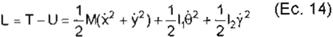
Consideramos la función de disipación de Rayleigh:
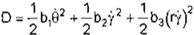 (Ec. 15)
(Ec. 15)
De tal forma que las ecuaciones de movimiento del sistema son:
Tenemos como coordenadas generalizadas (3): q = [O y]
110 + b1é = Ti
(Mr2 + r2 r;+(b2 + b3r2}1 = T2
(Ec. 16)
(Ec. 17)
 436
436
Expresando como variables de estado. se tiene:

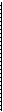
 o -bi o o 1)
o -bi o o 1)
Para el motor de tracción se utilizó un torque constante y el comportamiento del angulo y (de tracción) que se muestra en la Fig. 11.
 para:
para:
Mfi +12
XA
o Mr2
""1
:[ _/
SIMULACIONES
La dinámica del sistema fue simulada mediante el programa SimnonrM. Se utilizó una señal de torque como la mostrada en la figura 9 para el motor de
dírección.

 ...
...
º"

?
t
s
1
10
'2
u
1e
n
Figura 11.Ángulo y
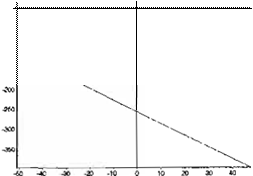
La trayectoria resultante está dada por la combinación de las ecuaciones 8, 9, 16 y 17. Graficando en forma paramétrica 8 y 9 se obtiene la trayectoria
del robot en el plano (Fig. 12)
 ---
---
-11)0
·•60
... º' •.e ' o " 1.1
Figura 9. Torque 1apl cado (detalle)
En la figura 1O se puede observar el comportamiento del ángulo e (ángulo de
dirección) con respecto al tiempo ante esta señal.
Figura 12. Trayectoria del robot en el plano
CONCLUSIONES
 181
181
"
•2
• í
/
• 1
'

 i -, • to 1l lA " it z;,
i -, • to 1l lA " it z;,
Figura 10. Ángulo O.
La planeación de movimiento en Robótica es un área en la que intervienen conceptos de control. modelado de sistemas y algunas veces de topología. En
este trabajo se muestra el análisis de movimiento de un robot móvil omnidireccional, este es un primer acercamiento hacia la planeación del movimiento.
Los resultados hasta el momento son simulados. se está trabajando en la validación experimental del modelo matemático. Una vez
 437
437

validado el modelo procederemos con el control.
Debido a que el modelo matemático es lineal, no se presentan comportamientos dinámicos complicados en la simulación (4 ).
REFERENCIAS
1. Mondragón-Parra, E.R .; Tame-Rivera , 8.; González-Hernández, H. G. (1996) Robot Móvil Omnidireccional Controlado por PC Remota para Seguimiento de Trayectorías Libres de Obstáculos. Memorias del 6to. Congreso Internacional de
Electrónica, Comunicaciones y Computadoras. Cholula, Puebla.
2. Kimbrelt, J. (1991) Kínematícs Ana/ysís and
Synthesis.
McGraw-Hill. Singapore .
3. Marion, J. B. (1965), Classical Dynamics.
Academic Press, N.Y.
4.
Woernle, c. (1995) Nontinear Motion Control of a Nonholonomic Mobile Platform by Exact Linearization. Proceedings of
IFTOMM 95'. Milano, ltaly.
 Un robot móvil omnidireccional permite el seguimiento (1) de diferentes tipos de trayectorias de manera fidedigna. En el presente trabajo se muestra un
análisis detallado del comportamiento estructural, cinemático y dinámico de un robot móvil omnidireccional. El robot que se analiza es el segundo
prototipo de la serie RoMEO (Robot móvil experimental ominidireccional).
Un robot móvil omnidireccional permite el seguimiento (1) de diferentes tipos de trayectorias de manera fidedigna. En el presente trabajo se muestra un
análisis detallado del comportamiento estructural, cinemático y dinámico de un robot móvil omnidireccional. El robot que se analiza es el segundo
prototipo de la serie RoMEO (Robot móvil experimental ominidireccional).

 X = 0.005 m; 2X ::: 0.01 rn.
X = 0.005 m; 2X ::: 0.01 rn.
 l
l
 V
V
 11
11

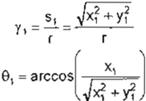 (Ec. 6)
(Ec. 6)



 Lo anterior se cumple, apoyado en un análisis geométrico. En a,, a , a , hay una
Lo anterior se cumple, apoyado en un análisis geométrico. En a,, a , a , hay una
 Las ecuaciones de Lagrange son:
Las ecuaciones de Lagrange son:

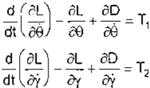 y (Ec. 10)
y (Ec. 10)


 ---
---
