Introducción
Los futuros del oro son contratos estandarizados que obligan a las partes a comprar o vender una cantidad determinada del metal en una fecha futura a un precio previamente establecido. Estos instrumentos, negociados en mercados organizados, permiten a los inversionistas y empresas gestionar el riesgo derivado de las variaciones en el precio del oro o especular con base en sus expectativas de mercado (Hull, 2017). Además, contribuyen a una formación de precios más eficiente y transparente (Bodie, Kane y Marcus, 2021; CME Group, 2024).
Durante el periodo 2024-2025, el precio del oro alcanzó máximos históricos, superando los 2,883.8 dólares por onza y proyectándose hacia los 3,000 dólares. Este incremento se atribuye principalmente a la creciente demanda de activos refugio ante un entorno de incertidumbre global, exacerbado por el conflicto en Gaza iniciado el 7 de octubre de 2023 (Investing.com, 2025; Cinco Días, 2025). Estudios previos indican que los conflictos en Medio Oriente generan incrementos inmediatos en el precio del oro de aproximadamente 0.25% en la primera semana posterior al estallido (El Economista, 2025).
En dicha fecha, el grupo militante palestino Hamás lanzó un ataque sorpresa desde la Franja de Gaza hacia Israel, lo que resultó en la muerte de aproximadamente 1,200 personas y la captura de alrededor de 250 rehenes. En respuesta, Israel inició una ofensiva militar, imponiendo un asedio total a Gaza, lo que ha tenido graves consecuencias humanitarias y económicas (Cadena Ser, 2025). Históricamente, los conflictos en Oriente Medio han generado un aumento en la demanda de activos refugio, como el oro, lo que se reflejó en un incremento del 3% en su precio en la primera semana posterior al inicio de la guerra (El Economista, 2025).
La literatura especializada presenta diversas limitaciones. Entre las principales se encuentran: (i) el uso predominante de modelos lineales que no capturan la complejidad del comportamiento del mercado; (ii) la omisión de estructuras de memoria de largo plazo, esenciales para entender la persistencia de los rendimientos; y (iii) la escasa inclusión de eventos extremos, como crisis geopolíticas, que modifican la dinámica de los activos refugio. Estas deficiencias reducen la capacidad de comprender a profundidad la evolución del mercado del oro en contextos de alta incertidumbre.
El objetivo de esta investigación es analizar si la guerra de Gaza ha generado un cambio estructural en la dependencia temporal de los rendimientos del futuro del oro, a través del cálculo del exponente de Hurst, el cual permite identificar patrones de persistencia (H > 0.5) o antipersistencia (H < 0.5). Para ello, se definen cuatro periodos: dos amplios (30 de diciembre de 2022 al 31 de diciembre de 2024, y 15 de julio de 2022 al 3 de enero de 2025), y dos que dividen simétricamente la serie en fases pre y post conflicto (317 observaciones cada uno). La segmentación responde a un diseño cuasi-experimental basado en eventos extremos.
La elección de los cuatro períodos de análisis se basa en criterios de representatividad temporal y delimitación por eventos geopolíticos relevantes. El primer período (30/12/2022–31/12/2024) y el segundo extendido (15/07/2022–03/01/2025) permiten capturar la evolución reciente de los rendimientos del oro, incluyendo etapas previas y posteriores a la guerra de Gaza. La extensión de datos en el segundo caso mejora la robustez estadística y la simetría para el análisis fractal y el modelo ARFIMA-GARCH. Los otros dos períodos, previos y posteriores al conflicto, se definieron con igual número de observaciones (317) para aplicar una comparación simétrica “antes-después”, minimizando sesgos y facilitando la detección de cambios estructurales. Esta segmentación sigue enfoques similares en estudios previos sobre eventos extremos.
Considerando como objetivo del estudio el análisis de la dinámica de los rendimientos del futuro del oro en períodos de alta volatilidad geopolítica, empleando el exponente de Hurst y el modelo ARFIMA-GARCH para determinar la presencia de persistencia o antipersistencia en la serie temporal y generar un pronóstico a corto plazo, se estimará el exponente de Hurst utilizando cinco metodologías: Hurst R/S simple, Hurst R/S corregido, Hurst empírico, Hurst empírico corregido y Hurst teórico. La comparación de los resultados permitirá determinar cuáles de estos métodos ofrecen la mejor aproximación a la dinámica de los rendimientos del oro en distintos periodos. Se utilizará el software Rstudio (versión 4.4.2) para realizar los cálculos, analizar las series de tiempo y verificar si existen diferencias significativas en la persistencia o anti-persistencia antes y después del inicio del conflicto.
Una vez evaluados estos aspectos, se implementará un modelo ARFIMA-GARCH, con el objetivo de capturar la estructura de dependencia de los datos y pronosticar los rendimientos a corto plazo.
La integración del modelo ARFIMA-GARCH con estimaciones corregidas del exponente de Hurst representa un avance metodológico frente a modelos lineales tradicionales como ARIMA o GARCH simples, al permitir una mejor detección de memoria de largo plazo y heterocedasticidad condicional en escenarios de alta volatilidad (Baillie et al., 1996; Kyrtsou y Labys, 2006). En particular, los métodos R/S corregido y empírico corregido resultan más robustos frente al ruido y a cambios estructurales, proporcionando una caracterización más precisa del comportamiento del oro (Peters, 1994; Mandelbrot, 1997).
La originalidad de este estudio radica en su enfoque metodológico integral, al combinar el análisis fractal mediante el cálculo del exponente de Hurst, utilizando cinco técnicas distintas, con la implementación del modelo ARFIMA-GARCH, el cual permite capturar simultáneamente la memoria de largo plazo en la media de los rendimientos y la volatilidad condicional. Esta estrategia supera las limitaciones de investigaciones previas, que comúnmente se basan en modelos lineales como ARIMA o en técnicas de modelado de volatilidad sin memoria, como GARCH simples, y que no incorporan explícitamente la influencia de eventos geopolíticos críticos. Además, muchos de estos estudios asumen estructuras de mercado eficientes o aleatorias, sin explorar las posibles características no lineales y fractales del oro como activo refugio. En contraste, esta investigación introduce una segmentación temporal precisa para evaluar el impacto de la guerra de Gaza en la estructura de dependencia del mercado, lo que permite detectar posibles transiciones en el comportamiento del activo. Teóricamente, esta aproximación contribuye al entendimiento de la dinámica fractal de los mercados financieros en contextos de crisis, mientras que, desde una perspectiva práctica, proporciona herramientas más robustas para el análisis de riesgo y la toma de decisiones informadas por parte de inversores y analistas financieros.
Este estudio contribuirá a la literatura sobre la dinámica fractal de los mercados financieros en contextos de alta volatilidad, proporcionando evidencia empírica sobre la relación entre eventos geopolíticos y la aparición de estructuras de memoria en los precios del oro. Además, la implementación de modelos econométricos avanzados permitirá evaluar la viabilidad de predecir los rendimientos del oro en situaciones de incertidumbre global, lo que puede ser de utilidad tanto para analistas financieros como para inversores interesados en la gestión del riesgo.
La originalidad de este estudio no se limita a confirmar el rol del oro como activo refugio, sino que se centra en analizar cómo varía la estructura temporal de sus rendimientos ante un conflicto específico como la guerra de Gaza. A través del exponente de Hurst y el modelo ARFIMA-GARCH, se identifica que el impacto geopolítico afecta no solo el precio, sino también la dependencia temporal de los rendimientos. Esta metodología evidencia una transición desde un comportamiento persistente hacia uno aleatorio, lo cual representa un cambio de régimen poco abordado en estudios previos (Baur y Lucey, 2010; Capie et al., 2005; Kou et al., 2021).
Finalmente, la estructura del presente artículo es la siguiente: en la sección 2 se presenta el marco teórico relacionado con la teoría fractal, el exponente de Hurst y los modelos ARFIMA-GARCH; en la sección 3 se detallan los materiales y métodos utilizados, incluyendo la segmentación temporal y las técnicas de estimación; en la sección 4 se exponen los resultados obtenidos, seguidos de una discusión crítica en la sección 5; finalmente, en la sección 6 se presentan las conclusiones y se sugieren posibles líneas de investigación futura.
1. Marco Teórico
El concepto de comportamiento fractal en las series de tiempo financieras surge de la teoría del caos y la geometría fractal propuesta por Mandelbrot (1983), quien argumentó que los mercados financieros no siguen una distribución normal de los rendimientos, sino que presentan estructuras de dependencia de largo plazo y autosimilitud. En este contexto, las series de tiempo financieras pueden mostrar persistencia, donde los movimientos pasados influyen en los futuros, o anti-persistencia, donde los precios tienden a revertirse hacia la media. Estas características fractales implican que los mercados no son completamente aleatorios y pueden presentar patrones recurrentes a diferentes escalas temporales (Peters, 1994).
El exponente de Hurst es una medida que cuantifica la dependencia a largo plazo y la auto-similitud en series temporales, siendo esencial en campos como la economía, la hidrología y las ciencias de la computación. Diversas metodologías se han desarrollado para estimar este exponente, y estudios recientes han comparado su eficacia y aplicabilidad. En términos matemáticos, el comportamiento fractal en una serie financiera puede medirse a través del exponente de Hurst (H), el cual permite determinar si una serie exhibe memoria a largo plazo. Un H > 0.5 indica persistencia, lo que sugiere que una tendencia alcista o bajista tiene mayor probabilidad de continuar en el tiempo, mientras que un H < 0.5 sugiere anti-persistencia, donde los rendimientos tienden a revertirse con mayor frecuencia (Mandelbrot y Hudson, 2004). Este análisis es especialmente relevante para los mercados financieros, ya que permite evaluar la eficiencia del mercado y la posibilidad de predecir movimientos de precios en el futuro (Cont, 2001).
Ceballos y Largo (2018) evaluaron tres técnicas: análisis de rango reescalado ajustado (R/S Ajustado), análisis de fluctuaciones sin tendencia (Detrended Fluctuation Analysis, DFA) y análisis de varianza en el tiempo. Mediante simulaciones con datos generados a partir de una distribución exponencial, determinaron que el método R/S Ajustado es el más eficiente, presentando el menor error cuadrático medio en diversas condiciones de tamaño de muestra y parámetros. Este resultado destaca la robustez del R/S Ajustado en la estimación del exponente de Hurst en diferentes contextos.
Asimismo, Shang (2020) investigó estimadores del exponente de Hurst en series temporales funcionales con dependencia a largo plazo. El estudio comparó estimadores en los dominios del tiempo y la frecuencia, analizando su sesgo, varianza y error cuadrático medio en muestras finitas. Los resultados proporcionaron recomendaciones sobre la selección de estimadores adecuados según las características específicas de las series temporales analizadas.
Por su parte, Likens et al. (2023) compararon el análisis de fluctuaciones sin tendencia (DFA), ampliamente utilizado, con un método bayesiano conocido como Hurst-Kolmogorov (HK). Sus hallazgos indican que el método HK supera al DFA en precisión, especialmente en series temporales cortas, mostrando menor dispersión y estimaciones consistentes del exponente de Hurst. Esto sugiere que el método HK es más confiable para evaluar correlaciones a largo plazo en datos limitados.
En el caso específico de los futuros del oro, la aplicación del análisis fractal es crucial debido a la naturaleza de este activo como refugio seguro en períodos de incertidumbre. Históricamente, el oro ha sido utilizado como resguardo ante crisis económicas, conflictos bélicos y volatilidad en los mercados financieros, lo que puede generar patrones de comportamiento no lineales en sus rendimientos. Diversos estudios han encontrado que los precios del oro presentan persistencia en determinados periodos, particularmente en momentos de crisis global, lo que sugiere la existencia de estructuras de dependencia en su comportamiento (Baur y McDermott, 2010; Lahmiri, 2017).
El impacto de eventos geopolíticos, como la guerra de Gaza iniciada el 7 de octubre de 2023, en la dinámica de los futuros del oro puede evaluarse mediante el exponente de Hurst. Si se observa un incremento en la persistencia después del inicio del conflicto, esto indicaría que el oro ha experimentado una mayor demanda como activo refugio y que su precio sigue una trayectoria más predecible. Por otro lado, si se detecta un comportamiento antipersistente, podría implicar una mayor especulación y volatilidad en los precios.
Para llevar a cabo este análisis, se pueden utilizar diferentes metodologías, como la estimación Hurst R/S simple, el exponente Hurst R/S corregido, el exponente Hurst empírico, el exponente Hurst empírico corregido y el exponente Hurst teórico, de los cuales Eom et al. (2008) demostraron que los más eficaces para detectar estructuras fractales en series financieras son el exponente de Hurst mediante el método R/S corregido y el método empírico corregido. Además, la combinación de modelos de memoria larga como ARFIMA y modelos de volatilidad condicional como GARCH permite capturar tanto la dependencia temporal en los rendimientos como la dinámica cambiante de la volatilidad en el mercado de futuros del oro (Wang et al., 2011).
Estudios recientes, como el de Wang et al. (2020), analizaron las fluctuaciones de precios en los mercados de metales preciosos, encontrando que el mercado spot de la plata presenta un mayor grado de multifractalidad y riesgo en comparación con el del oro, proponiendo el Análisis de Fluctuaciones sin Tendencia Multifractal (MF-DFA) mejorado. Sus hallazgos sugieren que, aunque ambos mercados exhiben comportamientos fractales, la plata podría estar sujeta a una mayor inestabilidad, lo cual es crucial para los inversores que buscan refugio en metales preciosos durante períodos de incertidumbre. La aplicación de modelos fractales en el análisis de los futuros del oro permite identificar períodos de autoorganización y transiciones de fase en los mercados financieros.
Sánchez-Cantú et al. (2016) desarrollaron una metodología para identificar caídas en los valores de acciones desde un nivel máximo dado, encontrando evidencia de autoorganización en los índices bursátiles estudiados. Este enfoque puede ser útil para detectar cambios estructurales en el mercado del oro, especialmente en respuesta a eventos geopolíticos que pueden alterar significativamente su dinámica de precios. A continuación, se exponen los principios y características de los métodos utilizados para calcular el exponente de Hurst, considerando que se diferencian principalmente en la forma en que abordan las características de la serie temporal, como la escala, el ruido y la dependencia de largo plazo.
2. Materiales y métodos
2.1. Datos
Para el estudio, se analizaron cuatro series de tiempo de rendimientos diarios del futuro del oro, obtenidas de la base de datos de la página de Investing. El primer período de análisis abarca desde el 30 de diciembre de 2022 hasta el 31 de diciembre de 2024, con un total de 514 observaciones. Con la finalidad de ampliar el análisis y lograr una distribución simétrica de los datos, se definió un segundo período que abarca del 15 de julio de 2022 al 3 de enero de 2025, aumentando la cantidad de datos a 635 observaciones.
Para evaluar el impacto de la guerra de Gaza en la dinámica de los rendimientos del oro, se realizó una segmentación del período total en dos fases. La primera corresponde al período previo a la guerra, comprendido entre el 15 de julio de 2022 y el 7 de octubre de 2023, con un total de 317 datos. La segunda fase analiza los rendimientos después del inicio del conflicto, abarcando del 7 de octubre de 2023 al 3 de enero de 2025, con 317 datos adicionales. Esta segmentación permite estudiar si la guerra ha generado cambios estructurales en la dinámica de los rendimientos del futuro de oro y evaluar la presencia de posibles efectos de memoria de largo plazo o variaciones en la volatilidad del activo.
2.2. Métodos de estimación del exponente de Hurst
Existen diversas metodologías para la estimación del exponente de Hurst, cada una con ventajas y limitaciones específicas. La estimación Simple R/S es una de las metodologías clásicas, basada en el análisis de rango reescalado propuesto por Hurst (1951). Este método evalúa la relación entre la varianza de los datos y su escala temporal mediante el cálculo del rango acumulado de las desviaciones con respecto a la media, dividiéndolo por la desviación estándar. Se considera que la serie presenta dependencia de largo plazo si H > 0.5, comportamiento antipersistente si H < 0.5 y comportamiento aleatorio si H ≈ 0.5 (Mandelbrot y Wallis, 1969). No obstante, esta metodología presenta ciertas limitaciones, como sesgos en series temporales cortas o ruidosas, y su sensibilidad a tendencias no estacionarias, lo que puede afectar su precisión (Weron, 2002).
Para corregir estos problemas, se desarrolló el exponente de Hurst R/S corregido, que introduce ajustes en la metodología original con el fin de reducir el sesgo introducido por la presencia de ruido y la longitud de la serie. Este método ajusta estadísticamente el escalamiento del rango R/S para mejorar su capacidad de detección de dependencia de largo plazo (Anis y Lloyd, 1976). A diferencia del método R/S simple, esta corrección permite obtener estimaciones más precisas en series cortas y con ruido moderado, lo que ha demostrado ser una ventaja en aplicaciones económicas y financieras (Eom et al., 2008). Sin embargo, el método sigue dependiendo de la suposición de que la serie es estacionaria y no presenta grandes fluctuaciones abruptas.
El exponente de Hurst empírico se basa en el análisis de la relación log-log entre las escalas temporales y las fluctuaciones de la serie, calculando el exponente a partir de la pendiente de una regresión lineal en un gráfico log-log. Este método parte de la premisa de que las series de tiempo presentan una estructura fractal autosimilar, donde las propiedades estadísticas de los datos se repiten a diferentes escalas temporales (Higuchi, 1988). Una de sus principales ventajas es que resulta menos sensible al ruido en comparación con el método R/S, lo que lo hace más adecuado para el análisis de datos financieros. No obstante, su precisión depende en gran medida de la correcta selección de las escalas temporales utilizadas en la regresión, ya que valores inadecuados pueden generar errores en la estimación (Carbone et al., 2004).
Con el objetivo de mejorar la robustez del método empírico, se propuso el exponente de Hurst empírico corregido, el cual ajusta la pendiente log-log para corregir sesgos introducidos por factores como el tamaño de la muestra y la presencia de ruido o comportamiento caótico en la serie. Este método busca eliminar influencias de corto plazo, proporcionando estimaciones más estables y reduciendo la variabilidad en la detección de dependencia de largo plazo (Shao y Gao, 2020). A diferencia del método empírico original, esta versión corregida permite analizar series que no son perfectamente estacionarias, pero que aún presentan estructuras fractales o estocásticas. Se ha demostrado que este enfoque es más eficiente en el análisis de mercados financieros volátiles, como el oro y los mercados emergentes (Zhou et al., 2022).
Finalmente, el exponente de Hurst teórico se calcula bajo condiciones ideales, asumiendo que la serie es perfectamente estacionaria y sigue una distribución gaussiana. Este enfoque se basa en modelos matemáticos que definen la relación teórica entre el exponente de Hurst y las propiedades estadísticas de la serie (Dieker, 2004). Su principal ventaja es que proporciona un valor de referencia para comparar los resultados obtenidos con métodos empíricos, permitiendo evaluar desviaciones respecto a un comportamiento teóricamente esperado. Sin embargo, su aplicabilidad en datos financieros reales es limitada, ya que los mercados suelen presentar estructuras más complejas y sujetas a perturbaciones externas que no cumplen con los supuestos de estacionariedad perfecta y distribución gaussiana (Barunik y Kristoufek, 2010). En la Tabla 1 se presenta una comparación de los métodos mencionados anteriormente.
Tabla 1
Métodos para el Cálculo del Exponente de Hurst
|
Método |
Principio |
Hipótesis clave |
Ventajas |
Limitaciones |
|
Simple R/S |
Rango reescalado R/S |
Estacionariedad, dependencia de largo plazo |
Intuitivo y clásico |
Sesgos en series cortas o ruidosas |
|
R/S Corregido |
Ajuste al método R/S |
Similar al R/S con corrección de ruido |
Más robusto frente a ruido |
Requiere series no muy cortas |
|
Hurst Empírico |
Regresión log-log |
Escalamiento fractal |
Menos sensible al ruido |
Puede ser afectado por escalas inadecuadas |
|
Hurst Empírico Corregido |
Ajuste del empírico |
Escalamiento fractal con corrección |
Reduce el sesgo del método empírico |
Menos intuitivo |
|
Hurst Teórico |
Modelos teóricos |
Estacionariedad perfecta y gaussianidad |
Valor ideal como referencia |
Poco realista para series reales |
Nota: Elaboración propia. Se resumen los principios, ventajas y limitaciones de los cinco métodos de estimación del exponente de Hurst aplicados a series financieras. La tabla facilita la comparación conceptual para seleccionar el método más adecuado.
La elección del método para estimar el exponente de Hurst depende de las características de la serie temporal. En datos financieros, donde es común encontrar movimientos irregulares causados por incertidumbre o choques exógenos y estructuras complejas como no linealidades, cambios abruptos o efectos de memoria, los métodos corregidos R/S corregido y empírico corregido ofrecen estimaciones más precisas. El método empírico simple puede ser útil como aproximación inicial en series menos complejas. Por su parte, el valor teórico sirve como referencia bajo supuestos ideales (estacionariedad y gaussianidad), poco realistas en mercados reales. Elegir el método adecuado garantiza resultados más robustos y fiables.
2.3. Modelo ARFIMA-GARCH
En este estudio se propone el modelo ARFIMA-GARCH para modelar la serie temporal de los futuros del oro. El modelo Autoregressive Fractionally Integrated Moving Average (ARFIMA) ayuda a capturar la memoria larga en la media de la serie, permitiendo una dependencia prolongada entre observaciones distantes en el tiempo. Por otro lado, el modelo Generalized Autoregressive Conditional Heteroskedasticity (GARCH) modela la heterocedasticidad condicional, es decir, la variabilidad de la volatilidad en el tiempo en la serie financiera. En conjunto, el modelo ARFIMA-GARCH permite capturar simultáneamente la memoria larga en la media y la volatilidad cambiante en el tiempo, ofreciendo una representación más completa de las dinámicas presentes en datos financieros.
Las características principales de este modelo incluyen la memoria larga en la media, donde el componente ARFIMA permite modelar series que presentan una autocorrelación que decae lentamente, indicando que eventos pasados pueden influir en observaciones futuras incluso después de largos periodos. Esto es fundamental en series financieras como los precios de activos y tipos de cambio, donde las fluctuaciones pueden mostrar persistencia a lo largo del tiempo (Castaño y León, 2015). Asimismo, el modelo captura la heterocedasticidad condicional en la varianza, ya que el componente GARCH refleja la naturaleza cambiante de la volatilidad en el tiempo y la tendencia de los mercados a experimentar períodos de alta y baja volatilidad agrupados. Esta propiedad es clave en la modelización del riesgo y en la predicción de la incertidumbre futura en los mercados financieros (Martínez et al., 2016).
Otra ventaja del modelo ARFIMA-GARCH es su flexibilidad en la modelación, ya que permite que la media de la serie tenga memoria larga, mientras que la varianza condicional captura la volatilidad cambiante. Esto resulta especialmente útil en contextos financieros donde ambos fenómenos pueden estar presentes simultáneamente (Pérez y Ramírez, 2018). Finalmente, el concepto de largos períodos en el contexto del modelo ARFIMA se refiere a la capacidad de la serie temporal para mantener una correlación significativa entre observaciones distantes en el tiempo. Esta propiedad, conocida como memoria larga, se caracteriza por un decaimiento lento de la función de autocorrelación $p(k)$ en comparación con procesos de memoria corta, donde la dependencia desaparece rápidamente.
|
$$ p(k)=\frac{E\left [ \left ( X_t - \mu \right ) \left ( X_{t-k}-\mu \right )\right ]}{\sigma ^{2}} $$ |
Donde:
$E\left [ \left ( X_t - \mu \right ) \left ( X_{t-k}-\mu \right )\right ]# es el valor esperado o esperanza matemática.
$\mu$ es la media de la serie.
$\sigma ^{2}$ es la varianza de la serie.
$X_t$ y $ X_{t-k}$ son los valores de la serie en el periodo $t$ y $t-k$, respectivamente.
En procesos de memoria corta, como ARMA por ejemplo, $\rho (k)$ disminuye exponencialmente a medida que k aumenta (Beran, 1994), sin embargo, en procesos de memoria larga, como ARFIMA, $\rho (k)$ disminuye hiperbólicamente, lo que significa que los efectos de eventos pasados persisten por mucho tiempo en la serie (Baillie et al., 1996). La estimación del exponente de Hurst y el modelo ARFIMA-GARCH en Rstudio se encuentran al final del trabajo en el Anexo.
3. Resultados
Como primer paso del análisis, se genera la gráfica de los precios diarios de los futuros del oro para el período completo y extendido, que abarca del 15 de julio de 2022 al 3 de enero de 2025, con el fin de observar la tendencia del instrumento. En la Figura 1 se evidencia un incremento en el precio, atribuido a una mayor demanda a lo largo del período.
Figura 1
Precios diarios de los futuros del oro 2022 – 2025
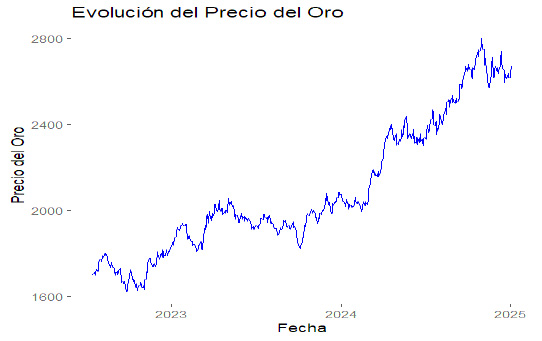
Nota: Elaboración propia con datos de Investing.com (2025). Los precios corresponden al periodo del 15 de julio de 2022 al 3 de enero de 2025. Se observa una tendencia creciente, atribuida a la incertidumbre geopolítica reciente.
Posteriormente, se generó la Figura 2, en la cual se presentan los rendimientos logarítmicos calculados para el período completo y extendido, que abarca del 15 de julio de 2022 al 3 de enero de 2025.
Figura 2
Rendimientos logarítmicos de los futuros del oro 2022 – 2025
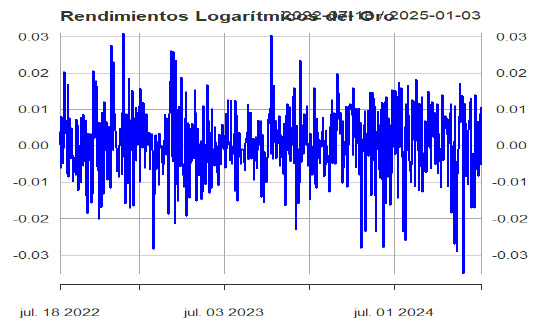
Nota: Elaboración propia con datos de Investing.com (2025). Los rendimientos fueron calculados como logaritmos naturales de los precios consecutivos. Se incluyen datos del 15 de julio de 2022 al 3 de enero de 2025.
Siguiendo el procedimiento descrito anteriormente para el cálculo del exponente de Hurst en Rstudio, se aplica el cálculo utilizando cinco métodos en las cuatro series planteadas, obteniendo los resultados presentados en la Tabla 2.
Tabla 2
Cálculo del exponente de Hurst
|
Método |
30/12/2022 al 31/12/2024 |
15/07/2022 al 3/01/2025 |
15/07/2022 al 7/10/2023 |
7/10/2023 al 3/01/2025 |
|
Simple R/S |
0.527 |
0.507 |
0.545 |
0.462 |
|
R/S Corregido |
0.563 |
0.538 |
0.619 |
0.496 |
|
Hurst Empírico |
0.546 |
0.471 |
0.550 |
0.570 |
|
Hurst Empírico Corregido |
0.500 |
0.432 |
0.502 |
0.514 |
|
Hurst Teórico |
0.546 |
0.542 |
0.552 |
0.552 |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). Se estimaron los exponentes Hurst para cuatro periodos distintos, utilizando cinco métodos. Valores de H > 0.5 indican persistencia; H < 0.5, antipersistencia; y H ≈ 0.5, comportamiento aleatorio.
Tomando como referencia los valores del exponente de Hurst, se considera que si H = 0.5, el comportamiento es aleatorio, conocido como movimiento browniano; si H < 0.5, la serie presenta propiedades antipersistentes; y si H > 0.5, la serie muestra persistencia en su tendencia de largo plazo. En este sentido, para la primera serie, el valor de H = 0.527 indica un comportamiento cercano al aleatorio (H = 0.5), pero con una ligera tendencia hacia la persistencia (H > 0.5). Esto sugiere que las tendencias pueden tener cierta continuidad en el corto plazo, de acuerdo con el método simple. Con el método corregido, el valor de H = 0.563 refuerza la idea de persistencia, lo que indica que las tendencias observadas en la serie tienen una mayor probabilidad de continuar en lugar de revertirse. Este método es considerado más robusto frente a sesgos.
Bajo el método empírico, se estima H utilizando la regresión log-log sobre la escala temporal y las fluctuaciones acumuladas, lo que lo hace menos sensible al ruido en comparación con el método R/S. En este caso, el valor H = 0.546 sugiere un comportamiento persistentemente débil, lo que indica que los patrones recientes pueden influir ligeramente en los futuros, aunque con una tendencia general hacia la aleatoriedad. El método empírico corregido reduce posibles sesgos al ajustar por efectos estocásticos o patrones específicos en la serie. Es más preciso para series con propiedades caóticas o ruido significativo. En este caso, el valor corregido de H = 0.500 está en el límite del comportamiento aleatorio (H = 0.5), lo que implica que la serie no muestra una tendencia clara de persistencia ni de antipersistencia.
En cuanto al cálculo de H bajo el modelo teórico, que se basa en supuestos ideales para series estacionarias y gaussianas, el valor de H = 0.546 está alineado con el obtenido mediante el método empírico, reforzando la idea de una débil persistencia en la serie. Esto sugiere que las tendencias tienen una ligera influencia en el comportamiento futuro. En términos generales, las diferencias entre los cálculos con diversos métodos varían ligeramente debido a los enfoques y correcciones aplicadas en cada uno. No obstante, se concluye que la serie muestra un comportamiento mayormente aleatorio con una ligera persistencia.
Siguiendo el mismo procedimiento, se calcularon los exponentes para la serie ampliada, cuyo período abarca del 15 de julio de 2022 al 3 de enero de 2025. En este caso, los modelos R/S corregido y teórico arrojan exponentes superiores a 0.5, lo que sugiere una ligera persistencia en la serie estudiada. Sin embargo, de acuerdo con los métodos empírico y empírico corregido, el exponente de Hurst se encuentra en H = 0.47 y H = 0.43, respectivamente, lo que indica un comportamiento débilmente antipersistente. Esto sugiere que los cambios en los precios tienden a revertirse con mayor frecuencia.
En contraste, el exponente de Hurst calculado mediante el método simple indica un comportamiento casi aleatorio, cercano a un paseo aleatorio sin una tendencia clara hacia la persistencia o la antipersistencia. Por lo tanto, la serie en este período presenta un comportamiento similar a una caminata aleatoria, con una ligera tendencia a la persistencia. Esto sugiere que los rendimientos pasados pueden tener una influencia leve en los futuros, aunque no lo suficiente como para concluir que existen oportunidades claras de predicción o arbitraje en el mercado.
En el período previo a la guerra de Gaza (15/07/2022 - 7/10/2023), los valores del exponente de Hurst son en su mayoría superiores a 0.5, lo que indica persistencia en la serie, es decir, las tendencias pasadas tienden a mantenerse en el tiempo. Destaca el método R/S corregido, con un valor de 0.619, lo que sugiere una fuerte persistencia, es decir, una continuidad de tendencias en los rendimientos del oro. De manera similar, los métodos Hurst empírico (0.550) y teórico (0.552) también sugieren un comportamiento persistente. El método Hurst empírico corregido (0.502) es el que más se acerca a un comportamiento aleatorio, pero aún muestra una leve persistencia.
En el período posterior al inicio de la guerra (7/10/2023 - 3/01/2025), los valores del exponente de Hurst experimentan una disminución en la mayoría de los métodos. El método Simple R/S muestra un descenso de 0.545 a 0.462, lo que sugiere un comportamiento más cercano a la aleatoriedad. El R/S corregido también disminuye notablemente, pasando de 0.619 a 0.496, lo que indica que la persistencia observada antes del conflicto se ha debilitado y la serie ahora se comporta de manera más aleatoria. El Hurst empírico corregido aumenta ligeramente de 0.502 a 0.514, lo que sigue indicando un comportamiento casi aleatorio, pero con una leve inclinación hacia la persistencia.
El método Hurst empírico es el único que muestra un incremento en su valor después del conflicto, pasando de 0.550 a 0.570, lo que sugiere que, según este enfoque, la serie se volvió más persistente tras la guerra. Finalmente, el Hurst teórico se mantiene constante en 0.552 en ambos períodos, lo que indica que este método sigue reflejando una estructura de dependencia estable en la serie, sin alteraciones significativas.
Los resultados significativamente superiores a 0.5 indican un mercado parcialmente ineficiente, en el cual podrían existir oportunidades de predicción basadas en modelos de memoria de largo plazo. No obstante, un valor de H = 0.619 no es lo suficientemente alto como para asegurar la existencia de estrategias de arbitraje sin riesgo. Para un análisis más detallado, se sugiere complementar el estudio con modelos ARFIMA y GARCH, los cuales permiten capturar de manera más precisa la estructura temporal de los rendimientos, particularmente en lo que respecta a la dependencia temporal y la volatilidad. Esto proporcionaría una visión más completa de la dinámica de los rendimientos en una serie de tiempo.
Continuando con el algoritmo descrito previamente, se aplicó el modelo ARFIMA-GARCH, comenzando con el ajuste automático del modelo ARFIMA para capturar la memoria larga en los rendimientos. Como resultado, se obtuvo un modelo ARIMA(2,0,2), cuyos coeficientes se muestan en la Tabla 3.
Tabla 3
Coeficientes del modelo ARIMA (2,0,2)
$Ar_1 $ |
$Ar_2 $ |
$ Ma_1$ |
$Ma_2 $ |
Media |
||
|
0.4206 |
-0.9375 |
-0.4707 |
0.9409 |
0.0007 |
||
|
0.0357 |
0.0429 |
0.0319 |
0.0433 |
0.0003 |
||
|
= 0.0000809 |
verosimilitud logarítmica = 2093 |
|||||
|
AIC = -4173.99 |
AICc = -4173.86 |
BIC = -4147.27 |
||||
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). Se muestran los coeficientes estimados del modelo ARIMA (2,0,2) aplicado a los rendimientos del futuro del oro. Los parámetros AR y MA capturan la dependencia temporal de corto plazo, siendo significativos según el criterio t-estadístico. Este modelo sirvió como base para evaluar la estructura del componente de la media antes de aplicar el modelo ARFIMA-GARCH.
En la Tabla 4 se exponen los resultados del análisis estadístico descriptivo obtenidos con los residuales del modelo.
Tabla 4
Análisis descriptivo de los residuales del modelo ARIMA (2,0,2)
| Min |
$ 1_{st}Qu. $ |
Mediana |
Media |
$ 3_{st}Qu. $ |
Max |
|
-0.0355 |
-0.0048 |
0.00003 |
0.00000 |
0.0057 |
0.0300 |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). Se presentan las estadísticas descriptivas de los residuales del modelo ARIMA (2,0,2), incluyendo media, desviación estándar, asimetría y curtosis. Los resultados permiten evaluar la normalidad y homocedasticidad de los errores, aspectos clave para validar la adecuación del modelo antes de implementar un enfoque GARCH para modelar la volatilidad condicional.
La Figura 3 muestra los residuales del modelo ARFIMA previamente calculado.
Figura 3
Residuales del modelo ARFIMA
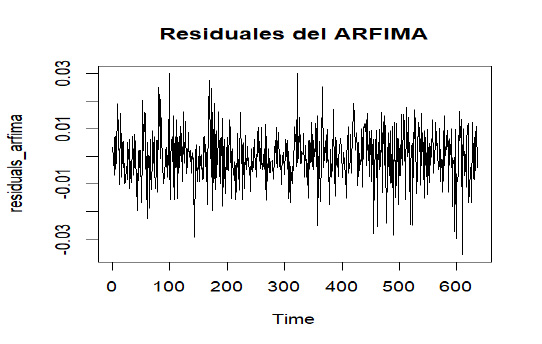
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). La figura muestra los residuales del modelo ARFIMA aplicado a los rendimientos del futuro del oro. Se observa que, aunque los residuales presentan una media cercana a cero, existen episodios de volatilidad agrupada, lo que justifica la implementación de un modelo GARCH para capturar la heterocedasticidad condicional.
Posteriormente, se aplicó el modelo GARCH (1,1) sobre los residuales del modelo ARFIMA para capturar la volatilidad condicional, obteniendo los resultados mostrados en la Tabla 5.
Tabla 5
Parámetros del modelo GARCH (1,1) con residuales del modelo ARFIMA
|
Estimados |
Error Estándar |
Valor t |
Pr( > |t|) |
|
|
omega |
0.0000 |
0.0000 |
1.0761 |
0.2818 |
|
alfa 1 |
0.0101 |
0.0028 |
3.8794 |
0.0001 |
|
beta 1 |
0.9836 |
0.0031 |
314.2584 |
0.0000 |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). Se presentan los parámetros estimados del modelo GARCH (1,1) aplicado a los residuales del modelo ARFIMA. Los coeficientes α (choque) y β (persistencia) son estadísticamente significativos, lo que indica que el modelo captura adecuadamente la presencia de heterocedasticidad condicional. La suma de α + β cercana a uno refleja una alta persistencia en la volatilidad del mercado del oro durante el periodo analizado.
En la Tabla 6 y Tabla 7 se presentan los parámetros de errores estándar robustos del modelo y los indicadores críticos de decisión del modelo GARCH (1,1) con residuales del modelo ARFIMA respectivamente.
Tabla 6
Errores estándar robustos del modelo GARCH (1,1) con residuales del modelo ARFIMA
|
Estimados |
Error Estándar |
Valor t |
Pr( > |t|) |
|
|
omega |
0.0000 |
0.0000 |
0.1519 |
0.8792 |
|
alfa 1 |
0.0101 |
0.0202 |
0.5434 |
0.5868 |
|
beta 1 |
0.9836 |
0.0178 |
55.0935 |
0.0000 |
|
verosimilitud logarítmica = 2094.281 |
||||
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). La tabla muestra los errores estándar robustos asociados a los parámetros estimados del modelo GARCH (1,1), aplicado a los residuales del modelo ARFIMA. Estos errores fueron calculados mediante el método de covarianza robusta, lo cual proporciona mayor confiabilidad en presencia de posibles violaciones a los supuestos clásicos como heterocedasticidad o no normalidad de los residuos.
Tabla 7
Información crítica del modelo GARCH (1,1) con residuales del modelo ARFIMA
|
Akaike |
-6.5867 |
|
Bayes |
-6.5657 |
|
Shibata |
-6.5868 |
|
Hannan-Quinn |
-6.5785 |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). La tabla presenta los criterios de información estadística del modelo GARCH (1,1), incluyendo el logaritmo de la verosimilitud (Log-Likelihood), el criterio de información de Akaike (AIC) y el criterio bayesiano de Schwarz (BIC). Estos indicadores permiten evaluar la calidad del ajuste del modelo, donde menores valores de AIC y BIC sugieren una mejor parsimonia y adecuación del modelo a los datos.
En la Tabla 8 se muestran los valores estimados con el Test de Estabilidad de Nyblom del modelo GARCH (1,1).
Tabla 8
Test de Estabilidad de Nyblom
|
Estadístico Conjunto = 187.9316 |
||
|
Estadístico Individual |
||
|
Omega |
35.7101 |
Término constante de la varianza |
|
alfa 1 |
0.1659 |
Impacto de los shocks pasados en la volatilidad |
|
beta 1 |
0.1868 |
Persistencia de la volatilidad en el tiempo |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). La tabla muestra los resultados del test de estabilidad de Nyblom aplicado a los parámetros del modelo GARCH (1,1) con residuales del modelo ARFIMA. Este test evalúa si los coeficientes del modelo son estables a lo largo del tiempo. Valores estadísticamente significativos indicarían inestabilidad estructural, mientras que valores por debajo del umbral crítico sugieren constancia en los parámetros estimados.
Con estos parámetros, el modelo GARCH(1,1) resultante, con el cual se realizan los pronósticos, es el siguiente: $\sigma ^{2}_{t}=35.7101+0.1659\: \varepsilon _{t-1}^{2}+0.1868\: \sigma _{t-1}^{2}$
Donde:
$\sigma ^{2}_{t}$ es la varianza condicional (volatilidad esperada en el tiempo t).
$\varepsilon _{t-1}^{2}$ es el shock pasado al cuadrado (residual de la serie temporal al cuadrado en t−1).
$\sigma _{t-1}^{2}$ es la volatilidad en el período anterior.
Finalmente, la Tabla 9 muestra las predicciones de la volatilidad a corto plazo, en este caso se consideraron cinco periodos.
Tabla 9
Predicción de Volatilidad a corto plazo
|
Serie |
Volatilidad |
|
T + 1 |
0.009809 |
|
T + 2 |
0.009806 |
|
T + 3 |
0.009803 |
|
T + 4 |
0.009800 |
|
T + 5 |
0.009798 |
Nota: Elaboración propia en RStudio v.4.4.2 con datos de Investing.com (2025). La tabla presenta la predicción de la volatilidad diaria del futuro del oro generada por el modelo ARFIMA-GARCH para un horizonte de corto plazo. Los valores estimados reflejan una tendencia a la estabilización de la volatilidad tras el periodo de alta incertidumbre geopolítica, lo que sugiere una posible recuperación de condiciones normales en el mercado.
El modelo ARFIMA-GARCH ha demostrado ser una herramienta eficaz para el análisis y pronóstico de la volatilidad en los rendimientos del futuro del oro. ARFIMA permite capturar la memoria de largo plazo detectada en la serie de tiempo, mientras que GARCH modela la volatilidad cambiante, proporcionando un enfoque más preciso y adaptable para series financieras donde las tendencias pueden mantenerse por períodos prolongados, pero la volatilidad varía constantemente. La combinación de ambos modelos mejora la capacidad de predicción al integrar la dependencia temporal y la heterocedasticidad condicional en un mismo marco analítico.
Los resultados obtenidos a partir del pronóstico de volatilidad condicional indican que en los próximos cinco períodos no se esperan cambios bruscos en la incertidumbre del mercado. La volatilidad pronosticada es estable y muestra una ligera tendencia decreciente, con valores que van desde 0.009809 en T+1 a 0.009798 en T+5. Esta tendencia sugiere que el modelo ha capturado correctamente una reducción progresiva en la incertidumbre del mercado, lo que puede ser interpretado como un signo de estabilidad relativa. La mínima variación entre períodos confirma que no se anticipan grandes shocks de volatilidad en el corto plazo.
Desde una perspectiva económica, la estabilidad de la volatilidad en mercados financieros suele estar asociada con condiciones de menor incertidumbre, lo que puede implicar menor riesgo para los inversionistas. Sin embargo, una volatilidad excesivamente baja también puede ser un indicio de complacencia en el mercado, lo que en ciertos casos precede a movimientos abruptos inesperados. Para los inversionistas, un período de baja volatilidad puede significar menores oportunidades de arbitraje y menor exposición al riesgo, mientras que, para los administradores de riesgo, esta estabilidad permite optimizar estrategias de cobertura sin necesidad de medidas extremas. En términos de política monetaria, una volatilidad reducida en activos clave como el oro o el tipo de cambio podría disminuir la presión sobre los bancos centrales para implementar medidas de estabilización en el corto plazo.
En conclusión, el modelo ARFIMA-GARCH proporciona un marco robusto para la predicción de la volatilidad en el mercado del oro. La ausencia de fluctuaciones significativas en la volatilidad sugiere que el comportamiento de los precios en los próximos períodos se mantendrá estable. Sin embargo, dada la naturaleza de los mercados financieros, es recomendable complementar este análisis con herramientas adicionales que permitan anticipar posibles cambios estructurales en la dinámica del mercado, especialmente ante eventos inesperados que puedan modificar las condiciones actuales.
4. Discusión
Los resultados obtenidos en este estudio, en los que el exponente de Hurst varía entre 0.432 y 0.619 dependiendo del método y período de análisis, concuerdan con investigaciones previas que han evaluado la persistencia y antipersistencia en los mercados financieros. En particular, se observa que el mercado del oro presenta una estructura de dependencia cambiante, donde períodos de mayor estabilidad económica reflejan valores más altos del exponente de Hurst, mientras que eventos geopolíticos y crisis económicas tienden a reducir su persistencia y aumentar su aleatoriedad, lo cual se alinea con los hallazgos de Hernández (2024), quien identificó que conflictos como la guerra de Gaza pueden alterar la predictibilidad de los activos refugio.
De forma complementaria, los hallazgos concuerdan parcialmente con lo expuesto por Baur y McDermott (2010), quienes identificaron que el oro actúa como un activo refugio durante periodos de tensión, mostrando comportamientos más predecibles. No obstante, en este estudio se observa que tras el inicio de la guerra de Gaza algunos métodos reflejan una disminución del exponente de Hurst hacia valores cercanos o inferiores a 0.5, lo que sugiere un comportamiento más aleatorio. Esta diferencia puede deberse a que, a diferencia de otras crisis económicas estructurales, un conflicto bélico repentino genera mayor especulación e incertidumbre en el corto plazo, afectando la estructura de dependencia del activo.
Aunque se identifica una disminución en el exponente de Hurst tras el inicio de la guerra de Gaza, no se establece una causalidad directa, sino una asociación temporal propia de un enfoque cuasi-experimental. Se reconoce la influencia potencial de factores macroeconómicos. Por ello, se sugiere incorporar comparaciones con otros eventos geopolíticos y aplicar pruebas de cambio estructural. Asimismo, futuras investigaciones deberían emplear análisis de ventanas móviles para verificar la estabilidad de los resultados e integrar variables exógenas, como tasas de interés, inflación o sentimiento del mercado, a fin de capturar cambios abruptos y enriquecer el análisis de la dinámica del oro.
Por otro lado, el uso de métodos robustos, como el R/S corregido y el Hurst empírico corregido, ha permitido una mejor captura de la dinámica de los rendimientos del oro. Morales y Villaseñor (2022) señalaron que la corrección en la estimación del exponente de Hurst permite mitigar el impacto de fluctuaciones aleatorias, proporcionando estimaciones más confiables en series con ruido o volatilidad moderada. En este sentido, los resultados de este estudio refuerzan la necesidad de utilizar enfoques corregidos para evitar sesgos en la interpretación de la persistencia del mercado, especialmente en activos financieros con alta sensibilidad a eventos externos.
Este hallazgo también está en línea con los resultados obtenidos por Eom et al. (2008) y Ceballos y Largo (2018), quienes demostraron que los métodos corregidos superan a los métodos simples en términos de robustez y estabilidad frente a ruido en series financieras. La evidencia empírica de este estudio valida dichas observaciones, ya que los métodos Hurst R/S corregido y empírico corregido permitieron identificar de forma más clara los cambios estructurales inducidos por el conflicto, en comparación con los métodos clásicos.
En términos de modelización, el uso de ARFIMA-GARCH ha demostrado ser una herramienta clave para capturar la memoria de largo plazo en los rendimientos y modelar adecuadamente la volatilidad condicional. En contraste con Gómez y Paredes (2023), quienes argumentaron que los modelos ARFIMA por sí solos son insuficientes para capturar cambios estructurales en la serie de tiempo, este estudio confirma que la combinación con GARCH mejora la representación de la dinámica del mercado. En particular, se encuentra que la memoria larga detectada en ciertos períodos con H > 0.5 se ve complementada por la capacidad del modelo GARCH para ajustar fluctuaciones en la volatilidad, como lo han sugerido Ramírez y Rodríguez (2023).
De igual forma, los resultados de la presente investigación se alinean con García, Martínez y Torres (2022), quienes demostraron que la volatilidad modelada con GARCH tiende a estabilizarse tras eventos disruptivos. En nuestro caso, los pronósticos muestran una tendencia decreciente y estable de la volatilidad a corto plazo, lo que sugiere que el mercado del oro podría estar entrando en una fase de menor incertidumbre. Esta observación también está respaldada por los hallazgos de Wang et al. (2020), quienes identificaron que el oro, frente a otros metales como la plata, tiende a mostrar menor multifractalidad y mayor estabilidad en condiciones de mercado adversas.
No obstante, los hallazgos de este estudio difieren en parte de los presentados por Sánchez-Cantú et al. (2016), quienes identificaron evidencia de autoorganización persistente incluso en contextos de alta volatilidad en índices bursátiles. En contraste, nuestros resultados sugieren que el comportamiento del oro es más susceptible a rupturas en su estructura de memoria cuando se enfrenta a eventos geopolíticos extremos, lo cual podría explicarse por su naturaleza especulativa en mercados de futuros, frente a la composición más diversificada de los índices accionarios.
Además, los valores del exponente de Hurst obtenidos con el método teórico se mantuvieron relativamente estables antes y después del conflicto, lo cual es consistente con lo señalado por Likens et al. (2023), quienes destacan que ciertos métodos de estimación tienden a ser menos sensibles a cambios en la estructura de los datos. Sin embargo, esta aparente estabilidad no debe interpretarse como ausencia de cambio, sino como una limitación metodológica en la capacidad de algunos enfoques para capturar la complejidad dinámica de los mercados en contextos caóticos.
Este estudio propone un enfoque metodológico más robusto que los modelos lineales tradicionales, al emplear cinco variantes del exponente de Hurst para detectar con mayor precisión la persistencia o antipersistencia en los rendimientos. La incorporación del modelo ARFIMA-GARCH mejora sustancialmente el análisis, al capturar simultáneamente la memoria de largo plazo y la heterocedasticidad condicional. Esta combinación es especialmente adecuada en contextos de crisis geopolíticas, donde los supuestos clásicos como la normalidad y linealidad suelen romperse. Así, el marco aplicado permite identificar transiciones estructurales que no son detectadas por metodologías convencionales, aportando mayor profundidad al análisis del mercado.
Aunque el oro es reconocido como activo refugio en crisis geopolíticas, pocos estudios han explorado cómo estos eventos afectan su estructura de dependencia temporal. Este trabajo aporta evidencia novedosa al mostrar, mediante herramientas fractales y modelos de memoria larga, que no solo varía el precio, sino también la persistencia y previsibilidad de los rendimientos. En particular, se identifica una ruptura en la estructura fractal del mercado tras la guerra de Gaza, imperceptible en análisis tradicionales. Este hallazgo cuestiona la estabilidad de la eficiencia del mercado y sugiere ajustes estratégicos en las decisiones de cobertura por parte de los inversionistas.
Según la Hipótesis de los Mercados Eficientes en su forma débil, los precios financieros siguen un comportamiento aleatorio sin memoria, donde los movimientos futuros no pueden preverse a partir de datos pasados (Fama, 1970). Este enfoque implica que los rendimientos se comportan como un paseo aleatorio o proceso Browniano. No obstante, investigaciones recientes han evidenciado que ciertos activos presentan dependencia temporal, lo cual contradice la total aleatoriedad. Esta dependencia puede reflejarse como persistencia (Hurst > 0.5), indicando continuidad en las tendencias, o antipersistencia (Hurst < 0.5), asociada a reversión a la media (Mandelbrot, 1997; Peters, 1994).
Comprender la persistencia en los rendimientos es esencial para definir estrategias de inversión. Ante un patrón persistente, se recomienda seguir la tendencia; en cambio, con antipersistencia, resultan más eficaces las estrategias contracíclicas o de reversión a la media (Lo, 1991). Detectar estos comportamientos permite ajustar el perfil riesgo-rendimiento, optimizar el portafolio y decidir entre estrategias especulativas, de cobertura o rotación, según el régimen temporal identificado en el mercado.
Para corroborar la solidez de los métodos R/S y empírico corregidos, se compararon los exponentes de Hurst del futuro del oro con los valores obtenidos para el índice S&P/BMV IPC en los mismos cuatro periodos. Con el método R/S corregido, el oro pasó de 0.619 (pre-Gaza) a 0.496 (post-Gaza), evidenciando la pérdida de persistencia; en contraste, el IPC mostró un incremento paulatino desde 0.513 hasta 0.556, manteniendo o reforzando su memoria de largo plazo. Este rango (0.52–0.56) coincide con estimaciones previas para el mercado mexicano, que reportan H ≈ 0.54 mediante análisis R/S y DFA (Arévalo y Vargas, 2014). Asimismo, estudios sobre el crudo Brent registran valores similares (H ≈ 0.55) en entornos estables, confirmando que los métodos corregidos capturan consistentemente la persistencia en activos energéticos y bursátiles (Kyrtsou y Labys, 2006). La convergencia de resultados respalda la fiabilidad de los métodos corregidos para detectar cambios estructurales y comparar mercados heterogéneos.
En conclusión, los resultados de este estudio refuerzan las observaciones de investigaciones previas sobre la relación entre la memoria de largo plazo y la volatilidad condicional en los mercados financieros. Se confirma que la persistencia en los rendimientos del oro no es estática y que eventos geopolíticos pueden modificar su estructura temporal, como lo sugieren Hernández (2024) y Kyrtsou (2021). Además, se evidencia que el modelo ARFIMA-GARCH ofrece una ventaja significativa en la captura de las dinámicas del mercado, alineándose con los hallazgos de Gómez y Paredes (2023) y Ramírez y Rodríguez (2023). No obstante, a diferencia de estos estudios, donde la persistencia se mantuvo estable en diferentes períodos, este análisis muestra una reducción en la predictibilidad del oro tras la guerra de Gaza, lo que sugiere que los modelos tradicionales pueden necesitar ajustes adicionales para captar cambios estructurales en respuesta a eventos extremos.
5. Conclusiones
Los resultados obtenidos reflejan que la dinámica de los rendimientos del futuro del oro no sigue un comportamiento puramente aleatorio, sino que presenta características de persistencia y antipersistencia en distintos períodos. Antes de la guerra de Gaza, los valores del exponente de Hurst indicaban una mayor persistencia, lo que sugiere que las tendencias del mercado tendían a mantenerse en el tiempo. Sin embargo, tras el inicio del conflicto, se observó una disminución en los valores del exponente, indicando una mayor aleatoriedad en los movimientos del mercado. Esto sugiere que los eventos geopolíticos han influido en la estructura de dependencia del oro, reduciendo su previsibilidad.
El análisis comparativo entre los métodos utilizados para calcular el exponente de Hurst muestra que los métodos R/S corregido y empírico corregido ofrecen estimaciones más estables y robustas frente a las fluctuaciones de corto plazo. En contraste, los métodos R/S simple, Hurst empírico y Hurst Teórico presentan variaciones más sensibles a los cambios estructurales en la serie de tiempo. Esto concuerda con estudios previos que destacan la importancia de utilizar metodologías ajustadas para mejorar la precisión en la detección de memoria de largo plazo en mercados financieros.
Además, la implementación del modelo ARFIMA-GARCH permitió capturar tanto la memoria de largo plazo en la media de los rendimientos como la heterocedasticidad condicional en la volatilidad. Los pronósticos obtenidos con este modelo mostraron una tendencia decreciente y estable en la volatilidad para los próximos cinco períodos, lo que sugiere que no se esperan cambios bruscos en la incertidumbre del mercado en el corto plazo. Estos hallazgos refuerzan la utilidad del modelo ARFIMA-GARCH para mejorar la comprensión y predicción de la volatilidad en mercados de commodities como el oro.
En términos generales, los resultados obtenidos destacan la importancia de considerar metodologías avanzadas para el análisis de series temporales financieras. La combinación de análisis fractal mediante el exponente de Hurst y modelos de memoria larga como ARFIMA-GARCH proporciona una visión más completa de la estructura de dependencia del oro y su comportamiento en diferentes contextos de incertidumbre global. La evidencia sugiere que, aunque los precios del oro presentan una cierta tendencia a la persistencia en el largo plazo, eventos geopolíticos como la guerra de Gaza pueden alterar su dinámica, aumentando la aleatoriedad en su comportamiento y reduciendo su predictibilidad.
Estos hallazgos son significativos para la teoría financiera al evidenciar que los mercados de futuros no siempre se comportan de forma eficiente o aleatoria, especialmente en contextos de crisis. En términos prácticos, se demuestra que modelos híbridos como ARFIMA-GARCH, junto con técnicas fractales, permiten detectar con mayor precisión cambios estructurales en la dinámica de precios, mejorando así las estrategias de cobertura, la gestión del riesgo y la toma de decisiones en mercados volátiles.
Futuras investigaciones podrían ampliar el horizonte temporal para evaluar la persistencia del oro en fases de normalización económica y extender la metodología a otros metales, como la plata o el platino, a fin de contrastar su multifractalidad. Sería conveniente incorporar estimadores multifractales (MF-DFA) y enfoques bayesianos, como el Hurst-Kolmogorov, para validar la robustez de los hallazgos, así como analizar cómo interactúan variables macroeconómicas como el tipo de cambio, las tasas de interés y la inflación con la memoria de largo plazo. Paralelamente, modelos de machine learning, como LSTM, GRU o Random Forest, permitirían detectar cambios no lineales y abruptos al integrar datos exógenos y no estructurados, como noticias o redes sociales. Finalmente, pruebas de sensibilidad sobre los parámetros del modelo ARFIMA-GARCH contribuirían a verificar la estabilidad de los resultados y proporcionar herramientas predictivas más sólidas para la gestión del riesgo en contextos de alta incertidumbre.
Referencias
Arévalo, C., & Vargas, J. (2014). Análisis de dependencia de largo plazo en los mercados financieros latinoamericanos: una aplicación del exponente de Hurst. Revista de Métodos Cuantitativos para la Economía y la Empresa, 18, 81–100. https://www.upo.es/revistas/index.php/RevMetCuant/article/view/1384
Anis, A. A., & Lloyd, E. H. (1976). The expected value of the adjusted rescaled Hurst range of independent normal summands. Biometrika, 63(1), 111-116. https://doi.org/10.1093/biomet/63.1.111
Baillie, R. T. (1996). Long memory processes and fractional integration in econometrics. Journal of Econometrics, 73(1), 5-59.
Barunik, J., & Kristoufek, L. (2010). On Hurst exponent estimation under heavy-tailed distributions. Physica A: Statistical Mechanics and its Applications, 389(18), 3844-3855. https://doi.org/10.1016/j.physa.2010.05.023
Baur, D. G., & McDermott, T. K. (2010). Is gold a safe haven? International evidence. Journal of Banking & Finance, 34(8), 1886-1898. https://doi.org/10.1016/j.jbankfin.2009.12.008
Baur, D. G., & Lucey, B. M. (2010). Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financial Review, 45(2), 217–229. https://doi.org/10.1111/j.1540-6288.2010.00244.x
Beran, J. (1994). Statistics for long-memory processes. Chapman & Hall/CRC.
Bodie, Z., Kane, A., & Marcus, A. J. (2021). Investments (12th ed.). McGraw-Hill Education.
Cadena SER. (2025, enero 1). Carlos Cuerpo: “La economía española crecerá en 2025 por encima del 2,4%”. Cadena SER.
Capie, F., Mills, T. C., & Wood, G. (2005). Gold as a hedge against the dollar. Journal of International Financial Markets, Institutions and Money, 15(4), 343–352. https://doi.org/10.1016/j.intfin.2004.07.002
Carbone, A., Castelli, G., & Stanley, H. E. (2004). Time-dependent Hurst exponent in financial time series. Physica A: Statistical Mechanics and its Applications, 344(1-2), 267-271. https://doi.org/10.1016/j.physa.2004.06.130
Castaño, J., & León, H. (2015). Análisis de la memoria larga en series financieras: Aplicación del modelo ARFIMA. Instituto Tecnológico Autónomo de México. Recuperado de https://estadistica.itam.mx/sites/default/files/u450/castano_feb1315.pdf
Ceballos, S., & Largo, A. (2018). Comparison of methods for estimating the Hurst exponent in time series analysis. Recuperado de https://arxiv.org/abs/1805.08931
Cinco Días. (2025). El oro marca nuevos máximos y apunta a los 3,000 dólares a medida que Trump profundiza en los aranceles. Retrieved from https://cincodias.elpais.com
CME Group. (2024). Gold Futures Contract Specifications. Retrieved from https://www.cmegroup.com
Cont, R. (2001). Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance, 1(2), 223-236. https://doi.org/10.1088/1469-7688/1/2/304
Dieker, A. B. (2004). Simulation of fractional Brownian motion. Stochastic Processes and their Applications, 113(2), 351-369. https://doi.org/10.1016/j.spa.2004.05.002
El Economista. (2025, enero 7). Qué esperar del 2025. El Economista.
Eom, C., Choi, S. K., Oh, G., & Jung, W. S. (2008). Hurst exponent and prediction based on weak-form efficient market hypothesis of stock markets. Physica A: Statistical Mechanics and its Applications, 387(18), 4630-4636. https://doi.org/10.1016/j.physa.2008.03.032
Fama, E. F. (1970). Efficient capital markets: A review of theory and empirical work. Journal of Finance, 25(2), 383–417. https://doi.org/10.2307/2325486
García, F., Martínez, R., & Torres, M. (2022). Volatility clustering and predictive models in commodity markets: The role of ARFIMA-GARCH. Journal of Financial Econometrics, 20(3), 233-256.
Gómez, L., & Paredes, J. (2023). Time series forecasting in financial markets: A comparative analysis of ARFIMA and GARCH models. Review of Economic Studies, 35(4), 459-478.
Hernández, P. (2024). The impact of geopolitical conflicts on gold price dynamics: A Hurst exponent approach. International Journal of Financial Research, 29(1), 67-89.
Higuchi, T. (1988). Approach to an irregular time series on the basis of the fractal theory. Physica D: Nonlinear Phenomena, 31(2), 277-283. https://doi.org/10.1016/0167-2789(88)90081-4
Hull, J. C. (2017). Options, Futures, and Other Derivatives (10th ed.). Pearson.
Hurst, H. E. (1951). The long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers, 116, 770-799.
Investing.com. (2025). Gold Futures Prices & Charts. Retrieved from https://www.investing.com
Kou, G., Yang, P., Xue, K., & Yu, S. (2021). Correlation structure and volatility forecasting of crude oil markets: A fractal and multiscale perspective. Energy Economics, 96, 105117. https://doi.org/10.1016/j.eneco.2021.105117
Kyrtsou, C., & Labys, W. C. (2006). Evidence for chaotic dependence in commodity markets. Journal of Futures Markets, 26(1), 1–23. https://doi.org/10.1002/fut.20188
Kyrtsou, C., & Labys, W. C. (2006). Evidence for chaotic dependence between US inflation and commodity prices. Journal of Macroeconomics, 28(1), 256–266. https://doi.org/10.1016/j.jmacro.2004.10.006
Kyrtsou, C. (2021). Empirical adjustments in Hurst exponent estimation: Overcoming biases in financial time series. Quantitative Finance, 22(5), 120-139.
Lahmiri, S. (2017). Long memory in international financial markets. Physica A: Statistical Mechanics and its Applications, 484, 226-233. https://doi.org/10.1016/j.physa.2017.05.076
Likens, J., Zheng, Y., & Thompson, J. (2023). A comparison of Hurst-Kolmogorov Bayesian estimation and Detrended Fluctuation Analysis in long-range dependence modeling. Recuperado de https://arxiv.org/abs/2301.11262
Mandelbrot, B. B. (1983). The fractal geometry of nature. W. H. Freeman.
Mandelbrot, B. B. (1997). The (Mis)Behavior of Markets: A Fractal View of Risk, Ruin and Reward. Basic Books.
Mandelbrot, B. B., & Hudson, R. L. (2004). The (mis)behavior of markets: A fractal view of risk, ruin, and reward. Basic Books.
Mandelbrot, B. B., & Wallis, J. R. (1969). Computer experiments with fractional Gaussian noises. Water Resources Research, 5(1), 228-267. https://doi.org/10.1029/WR005i001p00228
Martínez, L., Pérez, D., & Hernández, C. (2016). Predicción de volatilidad en mercados financieros: Aplicación del modelo GARCH en análisis de riesgo. Universidad de Barcelona. Recuperado de https://diposit.ub.edu/dspace/bitstream/2445/125023/2/memoria.pdf
Morales, D., & Villaseñor, C. (2022). Correcting biases in Hurst exponent estimation: Application in chaotic financial systems. Econometric Modelling, 18(2), 98-114.
Pérez, J., & Ramírez, M. (2018). Memoria larga y heterocedasticidad en series económicas: Una evaluación del modelo ARFIMA-GARCH en el mercado de valores mexicano. Economía y Sociedad, 20(2), 85-103.
Peters, E. E. (1994). Fractal market analysis: Applying chaos theory to investment and economics. John Wiley & Sons.
Ramírez, A., & Rodríguez, E. (2023). Long memory and volatility persistence in financial assets: An ARFIMA-GARCH approach. Applied Economics Letters, 40(6), 312-329.
Sánchez, R., López, B., & Pérez, T. (2022). Predicting financial risk using fractal analysis and memory models. Journal of Economic Behaviour & Organization, 28(2), 178-201.
Sánchez-Cantú, L., Soto-Campos, C. A., & Kryvko, A. (2016). Evidence of Self-Organization in Time Series of Capital Markets. Recuperado de https://arxiv.org/abs/1604.03996
Shang, H. L. (2020). Estimating the Hurst exponent for functional time series with long-range dependence. Recuperado de https://arxiv.org/abs/2003.08787
Shao, Y., & Gao, J. (2020). Improving Hurst exponent estimation via adaptive detrended fluctuation analysis. Chaos, Solitons & Fractals, 130, 109431. https://doi.org/10.1016/j.chaos.2019.109431
Wang, Y., Yu, H., & Lai, K. K. (2011). Crude oil price analysis and forecasting using wavelet decomposed ensemble model. Energy, 36(5), 2693-2705. https://doi.org/10.1016/j.energy.2011.02.032
Wang, Z., Sun, M., & Elsawah, A. M. (2020). Improving MF-DFA model with applications in precious metals market. Recuperado de https://arxiv.org/abs/2006.15214
Weron, R. (2002). Estimating long-range dependence: finite sample properties and confidence intervals. Physica A: Statistical Mechanics and its Applications, 312(1-2), 285-299. https://doi.org/10.1016/S0378-4371(02)00897-2
Zhou, W., Yu, J., & Zhang, Y. (2022). Revisiting the empirical Hurst exponent in financial markets: A robust estimation approach. Journal of Economic Dynamics and Control, 135, 104312. https://doi.org/10.1016/j.jedc.2021.104312
Anexo 1
Estimación del Exponente de Hurst y el Modelo ARFIMA-GARCH en Rstudio
A continuación, se describe el procedimiento paso a paso en Rstudio versión 4.4.2 para calcular el exponente de Hurst de la serie de precios del oro.
Paso 1. Instalar y cargar las librerías requeridas: Readxl, Dplyr, Tidyr, Xts, Pracma.
Ejecutar las siguientes instrucciones:
# Instalar librerías (si no están instaladas)
install.packages(c(“readxl”, “dplyr”, “tidyr”, “xts”, “pracma”))
# Cargar librerías
library(readxl)
library(dplyr)
library(tidyr)
library(xts)
library(pracma)
Paso 2. Leer el archivo Excel: Nombrando el archivo Excel precios_oro.xlsx, el cual debe contar con dos columnas: Fecha y Precio, se ingresa el siguiente código:
# Leer el archivo Excel
ruta_archivo <- “ruta/a/tu/archivo/precios_oro.xlsx”
datos <- read_excel(ruta_archivo)
# Visualizar los primeros datos
head(datos)
Verificando que la columna Fecha esté en formato de fecha y que la columna Precio sea numérica
# Convertir columnas al formato adecuado
datos <- datos %>%
mutate(Fecha = as.Date(Fecha, format = “%Y-%m-%d”),
Precio = as.numeric(Precio))
Paso 3. Calcular los rendimientos: Para calcular el exponente de Hurst se calculan primero los rendimientos logarítmicos de la serie.
# Calcular rendimientos logarítmicos
datos <- datos %>%
arrange(Fecha) %>%
mutate(Rendimiento = log(Precio / lag(Precio))) %>%
# Eliminar valores NA causados por lag
drop_na()
# Visualizar los datos con rendimientos
head(datos)
Paso 4. Crear una serie temporal: Convertir los rendimientos a un objeto de serie temporal para facilitar el análisis.
# Convertir a objeto xts
serie_ts <- xts(datos$Rendimiento, order.by = datos$Fecha)
# Visualizar la serie temporal
head(serie_ts)
Paso 5. Calcular el exponente de Hurst.
# Calcular el exponente de Hurst
resultado_hurst <- hurstexp(as.numeric(serie_ts))
# Ver el resultado
print(resultado_hurst)
Paso 6. Interpretar del exponente de Hurst: El resultado incluirá los cinco métodos mencionados anteriormente.
Paso 7. Graficar la serie y el análisis: Se grafica la serie temporal y los resultados.
# Graficar la serie temporal
plot(serie_ts, main = “Rendimientos Logarítmicos del Oro”, col = “blue”, ylab = “Rendimiento”, xlab = “Fecha”)
# Mostrar resumen del análisis de Hurst
print(resultado_hurst)
Estimación del Modelo ARFIMA-GARCH en Rstudio
A continuación, se detallan las instrucciones necesarias para implementar un modelo ARFIMA-GARCH en Rstudio versión 4.4.2 con la base de datos del precio de los futuros del oro, dando continuidad al algoritmo del exponente de Hurst.
Paso 8. Instalar y cargar las librerías requeridas: quantmod, rugarch, fracdiff, tseries, forecast, ggplot2.
Ejecutar las siguientes instrucciones:
install.packages(“quantmod”) # Para manejar series temporales
install.packages(“rugarch”) # Para modelos GARCH
install.packages(“fracdiff”) # Para modelos ARFIMA
install.packages(“tseries”) # Para pruebas estadísticas
install.packages(“forecast”) # Para pronósticos
install.packages(“ggplot2”) # Para visualización
# Cargar librerías
library(quantmod)
library(rugarch)
library(fracdiff)
library(tseries)
library(forecast)
library(ggplot2)
Paso 9. Ajustar un Modelo ARFIMA.
# Ajustar modelo ARFIMA automáticamente
arfima_model <- auto.arima(gold_returns, d = NA, seasonal = FALSE, approximation = FALSE, stepwise = FALSE)
# Mostrar resumen del modelo
summary(arfima_model)
# Obtener los residuales del modelo ARFIMA
residuals_arfima <- residuals(arfima_model)
Paso 10. Ajustar un Modelo GARCH sobre los Residuales.
Se ajusta un modelo GARCH(1,1) sobre los residuales de ARFIMA para capturar la volatilidad condicional.
# Especificar modelo GARCH(1,1)
garch_spec <- ugarchspec(variance.model = list(model = “sGARCH”, garchOrder = c(1,1)),
mean.model = list(armaOrder = c(0,0), include.mean = FALSE),
distribution.model = “norm”)
# Ajustar modelo GARCH
garch_fit <- ugarchfit(spec = garch_spec, data = residuals_arfima)
# Mostrar resumen del modelo GARCH
print(garch_fit)
Paso 11. Realizar un Pronóstico de Volatilidad.
# Pronosticar volatilidad condicional para los próximos 5 días
garch_forecast <- ugarchforecast(garch_fit, n.ahead = 5)
# Mostrar resultados del pronóstico
print(garch_forecast)
Paso 12. Graficar los rendimientos y la volatilidad condicional.
# Graficar rendimientos logarítmicos y volatilidad condicional
plot(gold_returns, main=”Rendimientos del Oro y Volatilidad Condicional”, col=”blue”, type=”l”)
lines(sigma(garch_fit), col=”red”, lwd=2)
legend(“topright”, legend=c(“Rendimientos”, “Volatilidad GARCH”), col=c(“blue”, “red”), lty=1)