Introducción
Ante la crisis del coronavirus SARS-CoV-2 se estima que 1.1 mil millones de estudiantes en todo el mundo dejaron de asistir a clases de forma presencial (UNESCO, 2020). En México, la iniciativa “Quédate en Casa”, implementada el 23 de marzo de 2020, promovió la migración de la educación al ámbito digital, decretándose la interrupción de las clases presenciales del 20 de marzo al 26 de abril (Secretaría de Educación Pública, 2020).
De acuerdo con Schmelkes (2020), en México se registraron 3.9 millones de estudiantes en modalidades presenciales y 760,000 en modalidades a distancia, distribuidos en más de 5,000 instituciones de educación superior, de las cuales 2,180 son de carácter público. La mayoría de los alumnos inscritos correspondían a programas de licenciatura (89%), 5.9% a programas de especialización y maestría, y 1% a doctorado. No obstante, la falta de acceso adecuado a la infraestructura digital, la carencia de capacitación en Tecnologías de la Información y las Comunicaciones (TIC), y las limitaciones de infraestructura, revelaron una situación de “vulnerabilidad en cadena” en el sistema educativo (Villela & Contreras Islas, 2021). Esta circunstancia amenazó el derecho a la educación y reveló fallas pedagógicas, lo que incrementó las tasas de deserción escolar.
En educación superior, las tasas de deserción en el ciclo escolar 2020-2021 fueron del 8.8% y en el ciclo 2021-2022 fueron del 8.1% (Schmelkes, 2020). Así, desde 2020 los estudiantes del mundo y de Instituciones de Educación Superior en México experimentaron dificultades para retornar al trabajo en laboratorio (Radhamani, Kumar, & Nizar et al., 2021). Los motivos fueron multidimensionales: mitigación comunitaria, distanciamiento social, adecuación de infraestructura, condiciones epidemiológicas de cada región, dificultades para el trabajo en línea, brecha digital de los estudiantes (Rodicio-García et al., 2020), falta de experticia del profesorado en ambientes de aprendizaje a distancia en México (Acuña Michel, Cuevas Salazar, & Angulo Armenta, 2022), y no disponibilidad de laboratorios virtuales (Jamshidi & Milanovic, 2022).
Como dato revelador, según Raman, Achuthan, Nair y Nedungadi (2022), el 72% de las investigaciones sobre laboratorios virtuales publicadas entre 2011 y 2021 fueron impulsadas por la digitalización, pero el efecto de la pandemia se reflejó claramente en la mayoría de estas publicaciones. Los principales contribuyentes fueron España, Alemania y Estados Unidos. Al respecto, y sin disponer de laboratorios virtuales, en este trabajo se planteó como solución, para el caso de un Programa de Ingeniería en Electrónica en México, el desarrollo de una plataforma experimental portátil, reprogramable, con posibilidad de simulación previa, con la que los alumnos podían trabajar sin hacinarse para subsanar la afectación a su adquisición de competencias prácticas.
La puesta en marcha de la propuesta no fue trivial: dichas plataformas debían emular sistemas reales (realización analógica-reconfigurable), adecuarse a los contenidos temáticos, y no había ni tiempo ni condiciones para implementar estrategias de validación del tipo Grupo de Prueba-Grupo Control. Además, los sistemas de educación en México operaban con dificultades presupuestales. Por lo tanto, para la justificación y validación de dicha propuesta, se realizó un proyecto de cinco etapas:
- Análisis epidemiológico-regional.
- Análisis de brecha digital de los estudiantes.
- Desarrollo de la plataforma experimental.
- Diseño de un tutorial para el uso de la plataforma.
- Validación estadística.
Las preguntas de investigación fueron: ¿se justifica el desarrollo de la plataforma experimental dado el impacto del COVID-19 en la región de influencia de la Universidad (Figura 1b)? ¿La brecha digital de los estudiantes les permite abordar su aprendizaje con esta propuesta? ¿La plataforma experimental cumple con ser económica, portátil, reconfigurable, y de fácil aprendizaje, sin penalizar los tiempos de las asignaturas implicadas? ¿Se valida estadísticamente la propuesta en términos de la mejoría del desempeño de los estudiantes?
La plataforma propuesta se muestra en la Figura 1a. Su parte medular es el arreglo analógico programable (FPAA por las siglas en inglés de Field Programmable Analog Arrays), un dispositivo reconfigurable eléctricamente que permite realizar funciones tales como: amplificación, integración/derivación, suma/resta, filtrado, comparación, multiplicación, generación de señales, entre otras. El FPAA permite realizar prototipos complejos en un tiempo reducido.
La plataforma completa consta de tarjetas de desarrollo AN231E04-DVLP4 para el FPAA AN231E04 del fabricante Anadigm (AN231E04 Datasheet Rev 1.2, n.d.), con un precio aproximado de $299 USD, y el Laboratorio Virtual Educativo ELVIS II+ de National Instruments, con un precio aproximado de $2,800 USD, o bien tarjetas de desarrollo USB Electronics Explorer Board (precio aproximado de $600 USD) o USB Analog Discovery de Digilent (precio aproximado de $270 USD). Estos dispositivos cuentan con osciloscopio, generador de señales arbitrarias, fuentes de alimentación, y analizadores de espectro, digitales y de señal dinámica.
Tras una revisión de la literatura, se encontraron varios estudios con orientación didáctica basados en FPAA. En (Pandiev, 2012), se proponen moduladores de amplitud. Las propuestas presentadas en (Hernández & Luna, s.f.) y (Galliere, 2007) incluyen manual y guía de prácticas. Parent, Hossain, King, Lagua y Gorman (2021) presentan una plataforma similar a la que aquí se reporta, que incluye videos de apoyo y control vía protocolos de escritorio remoto. Desafortunadamente, estos trabajos presentan alguna o varias de las siguientes desventajas: no son portátiles, no se estructuran como tutoriales, no se abordan para los contenidos de una asignatura completa y no presentan análisis estadístico de sus ventajas.
Considerando las desventajas mencionadas, en este estudio se exponen los hallazgos al utilizar la plataforma didáctica en un Grupo de Prueba de la asignatura de Ingeniería de Control en un Programa de Electrónica impartido en México, en contraste con dos grupos adicionales: uno que empleó simulaciones durante el periodo de confinamiento y otro que trabajó en el laboratorio previo a la pandemia de COVID-19.
Figura 1
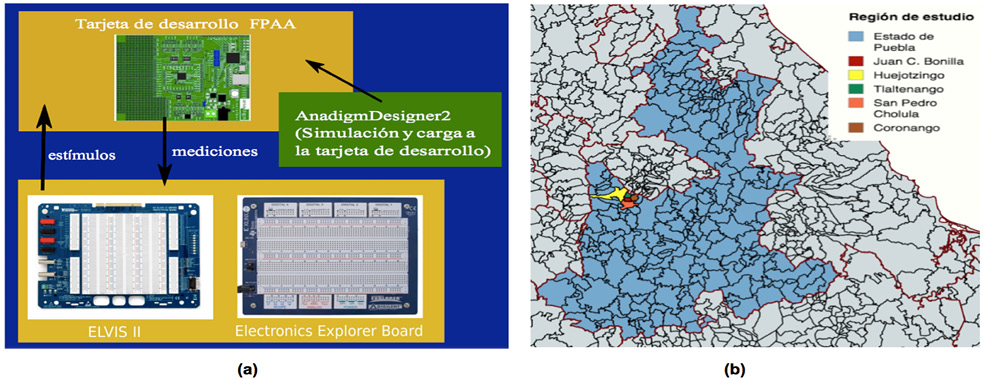
Nota. a) Plataforma experimental. b) Región de estudio, escala: 1:5,778,000.
El análisis comprendió cinco prácticas de laboratorio: filtro activo pasabanda de orden 16 (frecuencia central de 1 kHz, ancho de banda de 250 Hz, ganancia de 20 dB, ondulación de 1 dB y atenuación de 80 dB en la banda de rechazo), control proporcional-integral-derivativo (PID), modulación de amplitud y control de adelanto-atraso de fase de ordenes entero y fraccional. Se elaboró un tutorial compuesto por cuatro sesiones de dos horas cada una, con el objetivo de familiarizar a los estudiantes del Grupo de Prueba con la plataforma y promover el desarrollo de competencias con su utilización, integrando al tutorial dos de las cinco prácticas: modulación de amplitud y control de atraso-adelanto de fase de orden fraccionario. Se empleó un análisis de varianza con el objetivo de contrastar las calificaciones medias de cada grupo en cada actividad práctica.
1. Sustento teórico
1.1. Derivada e integral de orden fraccional
El cálculo fraccional ha sido objeto de estudio desde 1965, aunque sus fundamentos se remontan a los trabajos de Gottfried Wilhelm Leibniz (1 de julio de 1646 - 14 de noviembre de 1716) en el siglo XVII. No obstante, su intrincada naturaleza ha restringido su implementación práctica. La utilización de esta teoría en el modelado y control de sistemas (Chen & Luo, 2022) y en el diseño de filtros (Nako, Kaloudi, Tsirimokou, & Psychalinos, 2024) no fue hasta hace tres décadas. Además, su implementación en hardware es complicada debido a la ausencia de componentes de circuito que reproduzcan la expresión (1), conocidos como fractancias (Colín-Cervantes et al., 2021). Existen definiciones diversas para calcular derivadas e integrales de orden fraccional. De ellas, la definición de Riemann-Liouville establece lo siguiente (Colín-Cervantes et al., 2021):
|
$$ \mathfrak{D}_{t}^{\alpha } f(t)=\frac{1}{\Gamma(m-\alpha )}\left ( \frac{d}{dt} \right )^{m}\int_{\infty }^{t}\frac{f(\tau)}{(t-\tau )^{\alpha -m+1}}dt, \; \; \mathfrak{L}\left\{ \mathfrak{D}_{t}^{\alpha }f(t)\right\}=s^{\alpha }F(s) $$ |
donde $\alpha \in \mathbb{R}, m-1< \alpha < m\in \mathbb{N}$ y $\Gamma (\cdot )$ es la función Gamma. Para $\alpha > 0,\alpha < 0$ y $\alpha=0$, se obtienen respectivamente la derivada fraccional, la integral fraccional y la función identidad. $\mathfrak{L}\left\{ \mathfrak{D}_{t}^{\alpha }f(t)\right\}$ es la correspondiente transformada de Laplace con condiciones iniciales iguales a cero, donde $F(s)$ es la transformada de Laplace de $f(t)$ y $s^{\alpha }$ es el operador de Laplace de orden fraccional.
1.2. Modulación de Amplitud (AM)
En la modulación AM, la señal de información $u_{S}(t)=U_{Sm}\; \mathrm{cos}\; \omega_{S} t$ modula la amplitud de la señal portadora de alta frecuencia $u_{C}(t)$ ,manteniendo constante su fase. Si la señal de información se aplica a la envolvente compleja $g(t)=U_{Cm}+u_{S}(t)$, entonces la señal modulada se obtiene multiplicando $g(t)$ por una señal portadora $u_C(t)=\mathrm{cos}\; \omega _Ct$, lo que da como resultado (Pandiev, 2012):
|
$$ u_{AM}(t)=[U_{Cm}+u_S(t)]\; \mathrm{cos}\; \omega _Ct=\frac{U_{Cm}\; \mathrm{cos} \; \omega _Ct}{u_C(t)}+\frac{\frac{U_{Sm}}{2}\; \mathrm{cos}(\omega _C-\omega _S)t}{u_{LSB}(t)}+\frac{\frac{U_{Sm}}{2}\; \mathrm{cos}(\omega _C+\omega _S)t}{u_{USB}(t)} $$ |
La señal modulada consiste en la portadora no modulada $u_C(t)$ y dos señales de información en las frecuencias $\omega _C\pm \omega _S$ (banda lateral inferior $u_{LSB}(t)$ y banda lateral superior $u_{USB}(t)$. La demodulación de (2) puede realizarse al multiplicar (2) por una señal idéntica a $u_C(t)$, obteniendo como resultado:
|
$$ u_D(t)=\frac{U_{Cm}}{2}+\frac{U_{Cm}}{2}\mathrm{cos\; 2\omega _Ct}+\frac{U_{Sm}}{2}\mathrm{cos}\; \omega _St+\frac{U_{Sm}}{4}\mathrm{cos}\; (2\omega _C-\omega _S)t+\frac{U_{Sm}}{4}\mathrm{cos}\; (2\omega _C+\omega _S)t $$ |
Para recuperar $u_S(t)$, es necesario un filtro de paso bajo para eliminar los componentes en $2\omega _C$ y $2\omega _C\pm \omega _S$.
1.3. Control adelanto/atraso de fase de orden fraccional
Los compensadores de adelanto y atraso de fase modifican el margen de fase para lograr la respuesta transitoria deseada. En (Muñiz-Montero et al., 2016), se describe un procedimiento para la solución única y exacta de estos compensadores, pero de orden fraccional q, junto con su implementación con aproximaciones de orden entero de primer orden mediante:
|
$$ C_f(s)=K\left ( \frac{1+\alpha \tau s^{q}}{1+\tau s^{q}} \right )\approx K\left ( \frac{1+\alpha \tau ss^{q-1}}{1+\tau ss^{q-1}} \right )=K\left ( \frac{1+\alpha \tau s\left [ \frac{Bs+1}{s+B} \right ]}{1+\tau s\left [ \frac{Bs+q}{s+B} \right ]} \right )=\alpha \left ( \frac{s^{2}+\frac{\omega_z}{Q_z}s+\omega _{z}^{2}}{s^{2}+\frac{\omega _p}{Q_p}s+\omega _{p}^{2}} \right ),\; q\in (0,2), $$ |
|
$$ \omega _p=\frac{1}{\sqrt{\tau }},\; Q_p=\frac{\sqrt{\tau }B}{\tau +1},\; \omega _z=\frac{1}{\sqrt{\alpha \tau }},\; Q_z=\frac{\sqrt{\alpha \tau }B}{\alpha \tau +1}, $$ |
donde $K$ es la ganancia para satisfacer el error en estado estable, $\alpha$ y $\tau$ son los parámetros del controlador, y $q$ es el orden fraccional utilizado para limitar el valor inicial de la señal de control a un valor $u_0$(Tavazoei & Tavakoli-Kakhki, 2014). Estos parámetros se calculan utilizando:
|
$$ \alpha =\frac{\mathrm{uv\; tan}\left ( \frac{q\pi }{2} \right )-1}{\mathrm{v\; tan\left ( \frac{q\pi }{2} \right )-1}},\; \; \tau =\frac{1}{\omega _{BW}^{q}}\left [ \mathrm{v\; sin}\left ( \frac{q\pi }{2} \right ) -\mathrm{cos}\left ( \frac{q\pi }{2} \right )\right ],\; \; u=c\frac{c-\mathrm{cos}(p)}{c\; \mathrm{cos}(p)-1}, \; \; v=c\frac{c\; \mathrm{cos}(p)-1}{c\; \mathrm{sin}(p)}, \; \; c=10^{M/20}, $$ |
donde $K$, $M$ decibeles, y $p$ radianes ($-\pi /2\leq p\leq \pi /2$) son la ganancia, magnitud y fase que el compensador debe proporcionar a una frecuencia $\omega _{BW}$ para lograr el porcentaje de sobreimpulso deseado $M_p$, el error en estado estable $e_{ss}$ y el tiempo de asentamiento $t_s$. Para compensación de adelanto y de atraso de fase, y para una respuesta escalón, $q$ se calcula usando (Tavazoei & Tavakoli-Kakhki, 2014):
|
$$ q=\begin{Bmatrix} \frac{2}{\pi } \; \mathrm{tan}^{-1}\left ( \frac{u_0-K}{v(u_o-Ku)} \right )& \mathrm{si}\; \; v(u_0-Ku)> 0 \\ 1 & \mathrm{si}\; \; v(u_o-Ku)=0 \\ 2+\frac{2}{\pi}\; \mathrm{tan}^{-1}\left ( \frac{u_0-K}{v(u_0-Ku)} \right )& \mathrm{si}\; \; v(u_o-Ku)< 0 \\ \end{Bmatrix}. $$ |
1.4. Arreglos Analógicos Programables (FPAA)
Los FPAAs de la marca Anadigm utilizan tecnología de capacitores conmutados que posibilita la creación de resistencias equivalentes precisas y compactas a través de matrices de interruptores y capacitores (AN231E04 Datasheet Rev 1.2, s.f.). Los FPAA ofrecen alta precisión, baja sensibilidad a la temperatura y excelente linealidad. El modelo AN231E04 presenta una matriz de 2x2 Bloques Analógicos Configurables (CAB) (Figura 2a), cada uno con dos amplificadores operacionales, un comparador, un registro SAR (registro de aproximaciones sucesivas), y una tabla de consulta (LUT) que permite generar funciones arbitrarias. Además, admite reconfiguración en tiempo real.
El FPAA cuenta con siete puertos programables como entradas o salidas. El fabricante proporciona la plataforma de desarrollo AN231E04 y el software AnadigmDesigner2. Este software configura los bloques funcionales analógicos o CAM (Módulos Analógicos Configurables), a partir de los CAB, ofreciendo más de 35 CAM distintos (Figura 2b), entre los que se incluyen amplificadores, integradores, diferenciadores, multiplicadores, comparadores, osciladores y filtros. La interfaz del software es intuitiva (Figura 2c), facilitando la simulación de circuitos mediante la selección y conexión de módulos desde una biblioteca.
Tras la instalación, el software se inicia desde un ícono en el escritorio (Figura 2c, paso 1). El software muestra el espacio de trabajo. Incluye una ventana emergente para elegir el tipo de FPAA (paso 2: “seleccione el chip 231E04”). El menú “Edit” permite agregar un CAM o un FPAA adicional, mientras que el menú “Simulate” ofrece opciones para osciloscopios virtuales. La opción “Setup simulation” define la duración de las simulaciones, y “Begin simulation” inicia la simulación. El menú “Configure” transmite el diseño al hardware, mientras que “Settings” facilita la selección del puerto de la computadora para la programación. El menú “Tools” incluye instrumentos para diseñar filtros y controladores proporcional-integral-derivativo (PID).
2. Método
Este es un estudio cuantitativo-experimental donde se compara la forma en que distintas metodologías pedagógicas impactan en el rendimiento académico de los alumnos de la asignatura “Ingeniería de Control” de un Programa de Electrónica. El Grupo de Prueba, conformado por 19 hombres y 3 mujeres, llevó a cabo cinco prácticas de laboratorio utilizando la plataforma experimental de la Figura 1a al retornar a las clases tras la contingencia sanitaria. El Grupo Control 2, integrado por 14 hombres y 2 mujeres, completó las mismas prácticas por simulación durante la etapa no presencial de la contingencia. El Grupo Control 1, conformado por 11 hombres y 3 mujeres, realizó las mismas prácticas utilizando circuitos discretos antes de la contingencia (datos históricos disponibles antes de la contingencia). Se seleccionaron al azar calificaciones de 14 alumnos de cada grupo para cada práctica, lo que condujo a un total de 70 datos por cada grupo.
El mismo profesor evaluó las prácticas de los Grupos de Prueba, Control 1 y Control 2 con idénticos instrumentos de evaluación. Posteriormente, se llevó a cabo un análisis estadístico de esta información utilizando pruebas de Lilliefors y Levene como las reportadas en (Muñiz-Montero, et.al., 2025) o en (Bisquerra-Alzina, 1987), para confirmar el cumplimiento de los criterios de homogeneidad de varianzas y normalidad. Las calificaciones se compararon mediante análisis de Kruskal-Wallis para detectar diferencias entre las medianas de los tres grupos. Además, para evaluar la pertinencia del uso de la plataforma experimental, se llevó a cabo un análisis epidemiológico-regional que comprendió el periodo entre el 20 de marzo de 2020 y el 26 de agosto de 2021. El análisis epidemiológico-regional permitió evaluar el riesgo de los alumnos al trabajar en equipo, dado que los medios oficiales no ofrecían esta información por regiones (conjunto de municipios colindantes) (Muñiz-Montero et al., 2021).
Figura 2
FPAA AN231E04
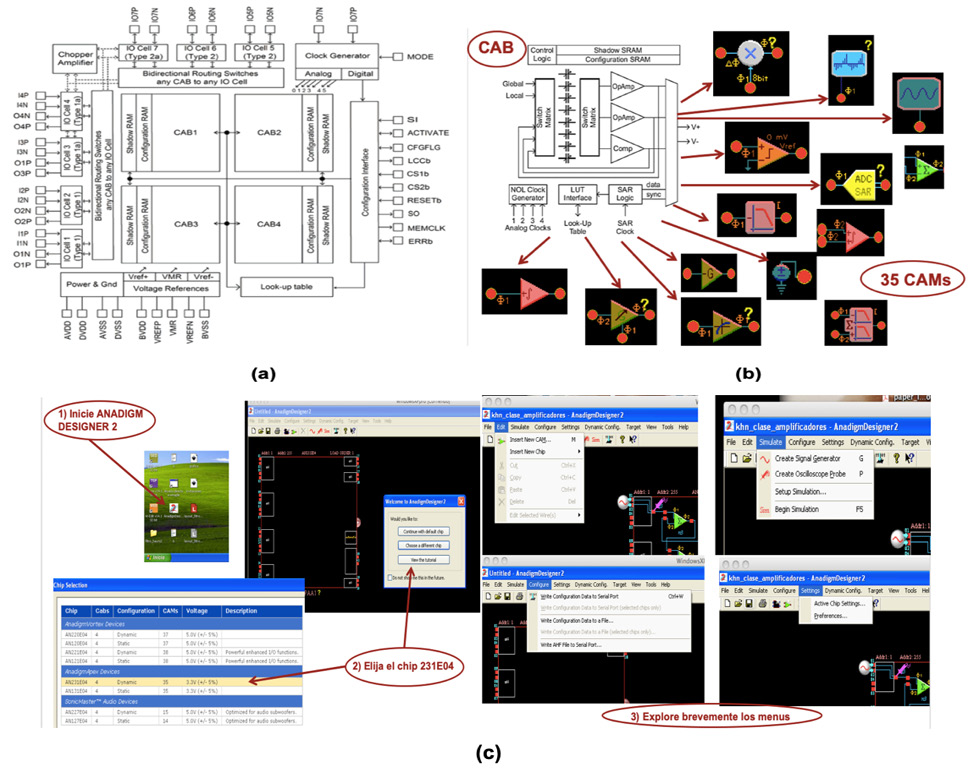
Nota. (a) Arquitectura. (b) CABs y CAMs. (c) Software AnadigmDesigner2.
El estudio se enfocó en el municipio de Juan C. Bonilla, donde se encuentra la Universidad, y en sus cuatro municipios adyacentes: Huejotzingo, Tlaltenango, Coronango y San Pedro Cholula (Figura 1b). La información relativa a las infecciones y fallecimientos diarios y acumulados se extrajo de la página de datos de COVID-١٩ de CONAHCYT (https://datos.covid-19.conacyt.mx).
También se llevó a cabo un análisis de la brecha digital entre los estudiantes a través de un cuestionario (vea la Figura 6). La recopilación y distribución de la información se realizó empleando la herramienta de Google Forms. La encuesta fue distribuida a 1,094 estudiantes pertenecientes a cuatro programas de licenciatura distintos: Electrónica, Sistemas Automotrices, Mecatrónica e Ingeniería Financiera. El grupo de estudio estuvo conformado por 285 estudiantes, garantizando un margen de error del 5%. Se examinó la disposición de los estudiantes a emplear plataformas experimentales en conjunto con clases semipresenciales, tutoriales en video y una estrategia de aprendizaje colaborativo centrada en proyectos. Cinco de las preguntas se centraron en establecer la magnitud de la brecha digital, mientras que las dos restantes evaluaron la disposición para emplear entornos de simulación y video-tutoriales.
3. Instrumento: Tutorial para el uso de la plataforma
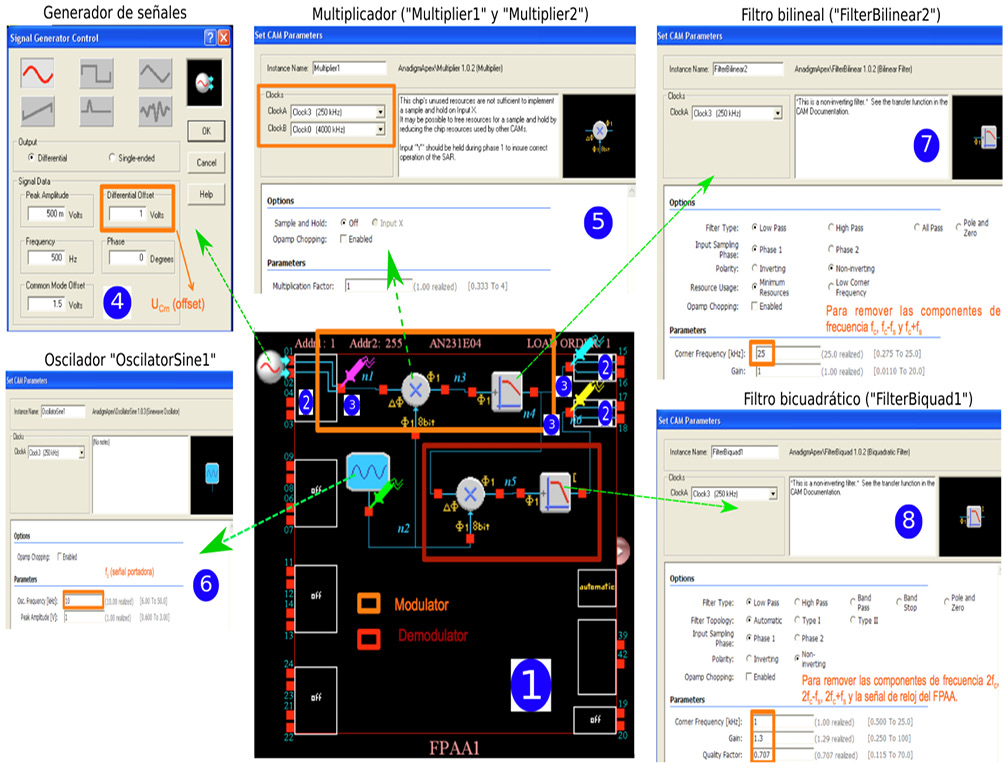
La Figura 3 muestra los detalles de la realización del modulador de AM. Se considera $U_{Cm}=1V$ y $U_{Sm}=0.5V$. Con el tutorial, se deben seguir los siguientes pasos:
- Agregue los CAMs (Edit→Inser New CAM) al espacio de trabajo (multiplicador modulador, multiplicador demodulador, oscilador senoidal, filtro bilineal y filtro bicuadrático) y realice con el mouse las conexiones indicadas.
- Configure los puertos con doble click y seleccione la opción “Bypass” (conexión directa por cable). Configure el puerto 1 como entrada (pines 01-02) y utilice los puertos 5 y 6 como salidas (pines 15-16 y 17-18).
- Agregue (Simulate→Create Oscilloscope Probe) una punta de osciloscopio a la entrada (rosa) y puntas de osciloscopio a las salidas (azul y amarillo).
- Agregue (Simulate→Create Signal Generator) con el generador de señales la señal moduladora: amplitud 500 mV, offset de 1 V, 500 Hz de frecuencia y 1.5 V de voltaje en modo común (tierra analógica).
- Configure (con doble click) ambos multiplicadores (CAMs “Multiplier”) con frecuencias de 250 kHz y 4000 kHz y factor de multiplicación unitario. La frecuencia 4 MHz es 16 veces mayor a 250 kHz, un requerimiento del CAM.
- Configure el oscilador (CAM “OscilatorSine1”) con frecuencia de oscilación 10 kHz (señal portadora) y amplitud 1 V.
- Configure (con doble click) el CAM “FiltrerBilinear2” como filtro pasabajas (de orden 1) con frecuencia de corte 25 kHz. Este filtro removerá las componentes de frecuencia fc, fc-fs y fc+fs.
- Configure el CAM “FiltrerBiquad1” como filtro pasabajas (de orden 2) con frecuencia de corte 1 kHz. Este filtro removerá las componentes de frecuencia 2fc, 2fc-fs y 2fc+fs, así como la señal de reloj del FPAA. El filtro tendrá ganancia 1.3 para compensar la atenuación del modulador y factor de calidad 0.7 para obtener una respuesta máximamente plana (para disminuir la distorsión harmónica).
- Asegúrese de que las conexiones salida-entrada de cada par de bloques conectados entre sí tenga la misma fase Φ1 o Φ2. Para cambiar la fase dé doble click en el CAM y seleccione “Phase1” o “Phase2”. Asegúrese de que todos los CAMs tengan la misma frecuencia de reloj (en este caso Clock3 a 250 kHz). En el menú seleccione la opción “Simulate”, luego “Setup Simulation” y seleccione el tiempo final de simulación. Ejecute la simulación dando click en el ícono “Sim” del menú.
- Compare sus resultados con los de la Figura 4. En las simulaciones, el tono de cada señal coincide con el tono de la punta del osciloscopio respectiva. La señal modulada (rosa) y la señal portadora (verde) coinciden con las amplitudes y frecuencias asignadas y/o calculadas anteriormente. La señal modulada (azul), presenta la forma de onda característica de una señal modulada en amplitud. La señal demodulada (en color amarillo) exhibe amplitud y fase idénticas a la señal que la modula, mostrada en rosa. La distorsión armónica total es del 1.2%.
Figura 3
Modulación de Amplitud
Para el control de orden fraccional, considere el sistema y la planta $G(s)$que se muestran en la Figura 5a. Con $K=1440$, se diseñó en (Muñiz-Montero, et.al., 2016) un sistema de control $C(s)$ de la forma (4) para satisfacer las siguientes especificaciones: tiempo de establecimiento=0.25 s; sobreimpulso=25%; error en estado estacionario=0.06%; señal de control inicial=2500. Estas especificaciones corresponden a un margen de fase deseado de 45.5 grados y una frecuencia de cruce de ganancia $\omega _{BW}=39$ rad/s. Esto a su vez corresponde a ajustar la ganancia de lazo del sistema M=3.76 dB y la fase en $p=24.1$ grados. Con este valor de $M$ se calculan $c, u$ y $v$ con (6), además de que se obtiene el orden fraccional $q=1.333$ con (7). Al sustituir los valores resultantes en $\alpha$ y $\tau$ de (6) en (4) y (5), se obtiene el controlador de la Figura 5a. Pasos a seguir:
Figura 4
Modulador AM
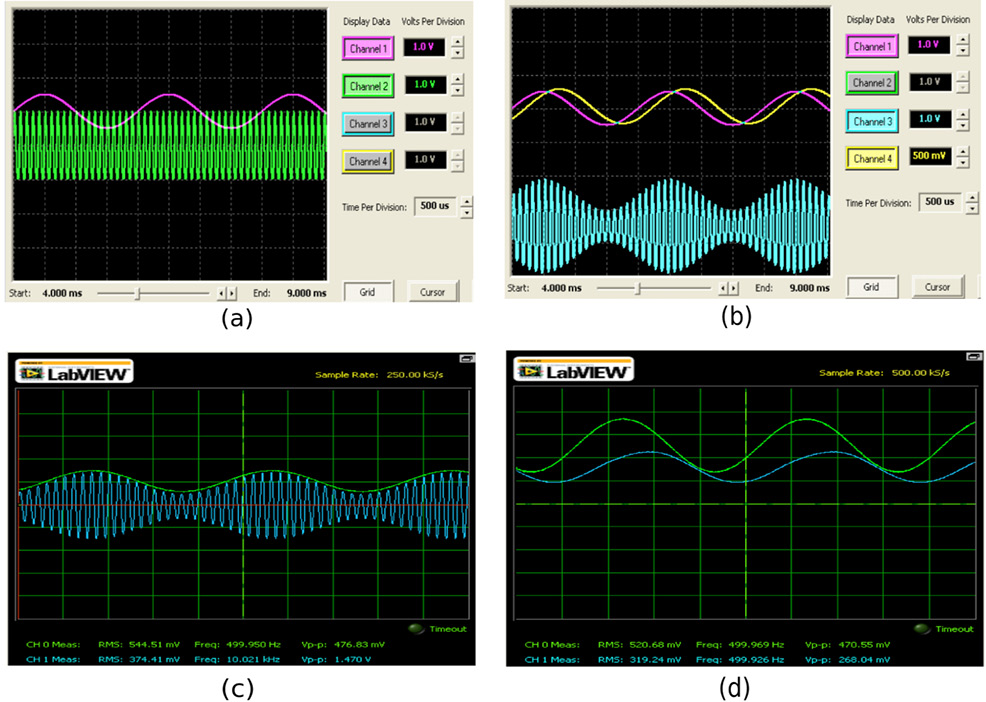
Nota: (a) Simulación en AnadigmDesigner2. (b) Señales demodulada y modulada. (c) Modulada (experimental). (d) Moduladora (verde) y demodulada (azul) experimental.
- Realice las conexiones de los elementos en la Figura 5c con los detalles de la Tabla en la Figura 5b. La planta G(s) está factorizada para habilitar su implementación con un integrador (“Integrator”) y dos filtros de paso bajo (“Filter Bilinear2” y “Filter Bilinear3”). El bloque “GainHold” con ganancia unitaria se introduce para establecer un retraso que estabilice la simulación.
- Configure el puerto 1 como entrada (pines 01-02) y el puerto 8 como salida (pines 19-20).
- Configure el generador de señales con una señal cuadrada de 500 Hz de frecuencia y 0.5 V de amplitud.
- La medición realizada con un osciloscopio Teledyne Lecroy HD4096 (Figura 6d) muestra un sobreimpulso del 16%, cumpliendo con las especificaciones al ser inferior al 25% esperado.
Figura 5 (parte 1)
Control adelanto-atraso de fase fraccional
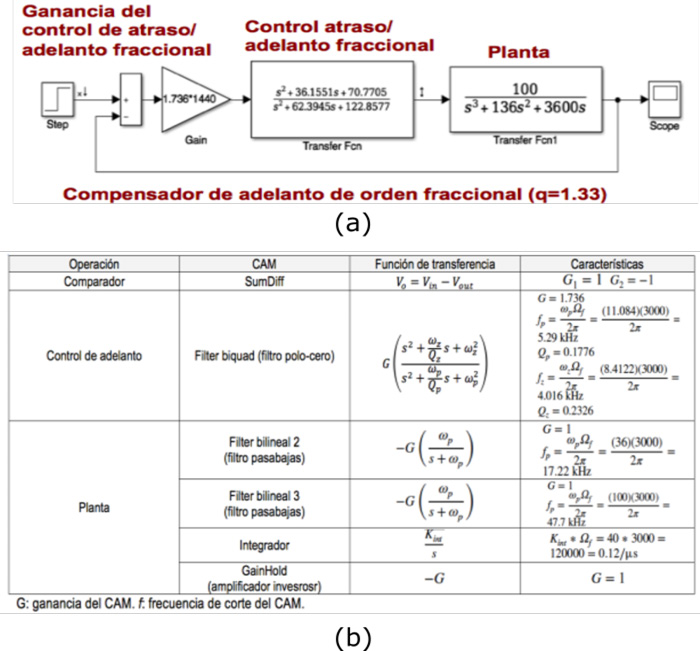
Nota: (a) Sistema en lazo cerrado. (b) Detalles de diseño de cada CAM.
4. Resultados y discusión
Respecto al análisis epidemiológico-regional, la economía de la región de la Figura 1b se sustenta en la agricultura, el comercio minorista, la manufactura y la producción de ladrillos. Algunos datos sobre esta región son: área, 391.52 km²; población, 291,229 habitantes; densidad poblacional, 743.8 habitantes/km²; cantidad de población en pobreza extrema, moderada, excepto en Juan C. Bonilla y Coronango; baja presencia de población indígena y alta vulnerabilidad al SARS-CoV-2, según Suárez-Lastra et al. (2020).
Figura 5 (parte 2)
Control adelanto-atraso de fase fraccional
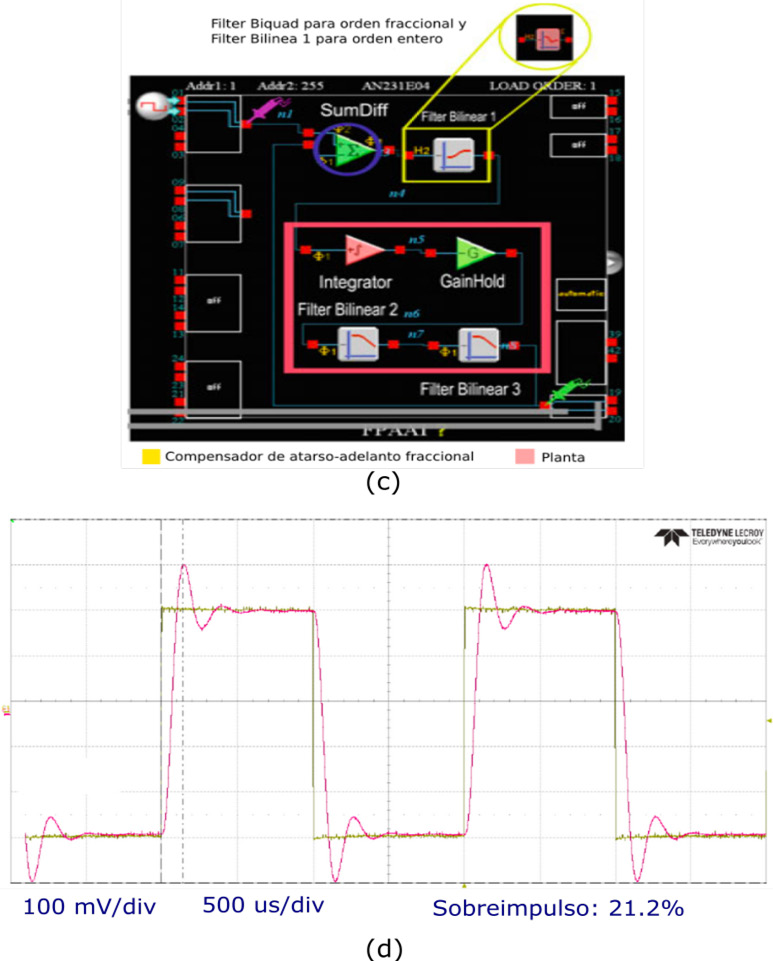
Nota. (c) Implementación en la FPAA. (d) Respuesta experimental del sistema.
Según el Catálogo de Localidades de la Secretaría de Desarrollo Social (SEDESOL, 2013), de los 217 municipios del estado de Puebla, Juan C. Bonilla, Huejotzingo, Tlaltenango, Coronango y San Pedro Cholula ocupan los lugares 184, 205, 202, 162 y 213 en términos de marginación, respectivamente. El Indicador de Marginación establece la falta de oportunidades de crecimiento en una región (CONAPO, 2010). En consecuencia, esta área tiene baja marginación, lo que sugiere que el nivel de brecha digital permite que los estudiantes utilicen las TICs.
Según datos del servicio https://datos.covid-19.conacyt.mx, en agosto de 2021 la región reportó 4,077 casos de COVID-19 y 494 muertes, lo que da una tasa de letalidad del 12.1%, casi un 70% superior al promedio nacional. Los datos indican que la Universidad se ubica en una región vulnerable, con alta tasa de letalidad y dinámica creciente de contagios durante el retorno a clases presenciales.
Figura 6
Análisis de la Brecha Digital
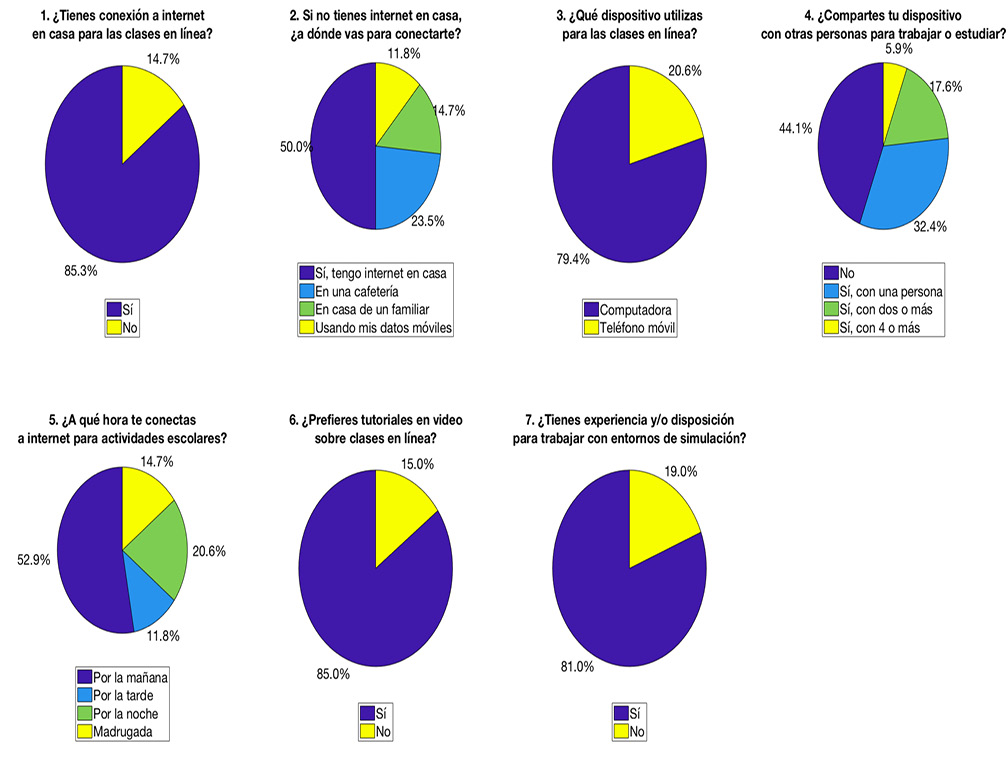
Respecto a la brecha digital, en mayo de 2021 un grupo de estudiantes universitarios seleccionado al azar completó una encuesta de siete preguntas en la herramienta “Forms” de Google. La encuesta se aplicó a 1,094 estudiantes inscritos en cuatro programas académicos: Sistemas Automotrices, Electrónica, Mecatrónica e Ingeniería Financiera. La muestra final de 285 estudiantes aseguró un nivel de confianza del 95%.
Los datos de la Figura 6 señalan que en mayo de 2021 existía una brecha digital notable entre los estudiantes, la cual, sin embargo, no obstaculizaba la realización de actividades semipresenciales (preguntas 6 y 7). El 14% de los estudiantes no tenían acceso a Internet en sus hogares, el 11% dependía de datos móviles, el 24% utilizaba cibercafés y el 20% usaba sus dispositivos móviles para ver tutoriales en línea. El 60% de los alumnos compartía su dispositivo de acceso a Internet con miembros de su familia. El 85% de los estudiantes mostraba preferencia por la utilización de video tutoriales en lugar de las clases en línea. El 81% mostraba disposición para trabajar con entornos de simulación. Así, el uso de archivos de simulación para replicar laboratorios virtuales, o bien, para anticipar el uso de la plataforma experimental demostró ser factible.
La Tabla 1 muestra las calificaciones de los estudiantes en las cinco prácticas de laboratorio, P1 a P5. Los resultados de la prueba de Lilliefors muestran que, con valores $p$ de 0.0063, 0.0216 y 0.0253, las distribuciones de datos del Grupo de Prueba, Grupo 1 y Grupo 2 no son normales. Además, la prueba de Levene produjo un valor p de 5.7692e-07, lo que indica que las varianzas entre los tres grupos no son homogéneas, rechazándose por tanto la hipótesis de igualdad de varianzas. Al no cumplirse los supuestos de normalidad y homogeneidad de varianzas, se realizó la prueba de Kruskal-Wallis para comparar las medianas de los tres grupos. La prueba evidenció discrepancias significativas entre las medianas de los grupos. El correspondiente análisis bootstrap con un intervalo de confianza del 95% indicó que el Grupo de Prueba posee la puntuación media más alta de 9.1357, acompañado de un estrecho rango de confianza de [9.09, 9.18].
Tabla 1
Calificaciones de los estudiantes en las prácticas P1 a P5, para cada grupo
|
GRUPO DE PRUEBA |
GRUPO 1 |
GRUPO 2 |
|||||||||||||
|
P1 |
P2 |
P3 |
P4 |
P5 |
P1 |
P2 |
P3 |
P4 |
P5 |
P1 |
P2 |
P3 |
P4 |
P5 |
|
|
1 |
9.4 |
9.3 |
9.4 |
8.9 |
8.9 |
8.5 |
8.8 |
8.1 |
7.6 |
7.6 |
8.4 |
8.7 |
8.6 |
7.6 |
7.6 |
|
2 |
9.2 |
9.1 |
9.2 |
9 |
8.9 |
8.6 |
8.3 |
8.4 |
7.9 |
7.7 |
8.3 |
8.6 |
8.4 |
7.8 |
7.2 |
|
3 |
9.3 |
9.3 |
9.5 |
8.8 |
8.9 |
8.2 |
8.8 |
8.8 |
7.7 |
7.1 |
8 |
7.9 |
8.8 |
7.7 |
7 |
|
4 |
9.4 |
9.3 |
9.4 |
9.1 |
8.9 |
8.7 |
8.4 |
8.3 |
8.1 |
7.5 |
8.1 |
8.2 |
7.9 |
7.9 |
7.8 |
|
5 |
9.4 |
9.2 |
9.4 |
9 |
8.8 |
8.3 |
8.7 |
7.8 |
7.4 |
7.4 |
8.2 |
8.3 |
8.2 |
7.8 |
7.4 |
|
6 |
9.1 |
9 |
9.2 |
9 |
8.9 |
8.3 |
8.5 |
8.1 |
7.8 |
7.8 |
8.5 |
8.8 |
8.4 |
7.6 |
7.1 |
|
7 |
9.4 |
9.2 |
9.3 |
8.9 |
8.9 |
8.5 |
8.3 |
8.3 |
8 |
7.6 |
8.3 |
8.5 |
8.1 |
7.9 |
7.5 |
|
8 |
9.4 |
9.1 |
9.2 |
9 |
8.9 |
8.8 |
8.7 |
8 |
7.7 |
7.3 |
8.8 |
8.1 |
8.1 |
7.8 |
7.3 |
|
9 |
9.3 |
9 |
9.3 |
9.1 |
8.9 |
8.1 |
8.5 |
8.5 |
8.2 |
7.2 |
8.1 |
8.5 |
8.5 |
7.8 |
7.7 |
|
10 |
9.4 |
9.3 |
9.5 |
8.8 |
8.9 |
8.1 |
8.6 |
8.2 |
8 |
7.5 |
7.9 |
8 |
8 |
7.8 |
7.7 |
|
11 |
9.4 |
9.3 |
9.4 |
9 |
8.9 |
8.2 |
8.3 |
8 |
7.5 |
7.3 |
8.2 |
8.4 |
8.3 |
7.6 |
7.2 |
|
12 |
9.1 |
9.1 |
9.3 |
8.7 |
8.8 |
8.9 |
8.3 |
8 |
7.5 |
7.3 |
8.3 |
8.3 |
8 |
7.7 |
7.6 |
|
13 |
9.3 |
9.1 |
9.2 |
9 |
8.9 |
8.1 |
8.2 |
8.1 |
8.2 |
7.7 |
8.4 |
8.1 |
8.3 |
7.9 |
7.1 |
|
14 |
9.4 |
9.2 |
9.3 |
9.1 |
9 |
8.5 |
8.8 |
8.8 |
7.4 |
7.4 |
8.1 |
8.8 |
8 |
7.6 |
7.9 |
Nota. P1: Filtro de orden 16. P2: control proporcional-integral-derivativo (PID). P3: modulación de amplitud. P4: control de adelanto-atraso de fase de orden entero. P5: control atraso-adelanto de orden fraccionario. Elaboración propia.
El Grupo 1 y el Grupo 2 presentan puntuaciones medias de 8.15 (intervalo de confianza: [8.03, 8.25]) y 8.06 (intervalo de confianza: [7.95, 8.17]), respectivamente, mostrando una mayor dispersión. Se observa que la intervención en el Grupo de Prueba tuvo un efecto positivo significativo en las calificaciones de los estudiantes: este grupo mejoró aproximadamente 10% su calificación con respecto a los otros dos grupos en una escala de 10 puntos. Así, la plataforma experimental cumple con ser económica, portátil y de fácil aprendizaje. Además, más allá de dos horas adicionales de apoyo en video, no se modificaron las sesiones de aprendizaje. De esta forma, lejos de implicar más tiempo de trabajo para los estudiantes, la posibilidad de realizar prototipos rápidamente facilitó la comprensión teórica y la ejecución de las prácticas.
En la Introducción de este trabajo se mencionaron estudios identificados en la literatura que abordan el diseño de sistemas analógicos con FPAA de forma didáctica, pero ninguno de ellos lo hace en contexto COVID-19, y ninguno incorpora análisis de tipo epidemiológicos-regional, de brecha digital y de validación estadística para medir su eficiencia. En (Pandiev, 2012), se carece de la estructura de un tutorial, solamente se reporta el experimento. En (Hernández & Luna, s.f.) sí se incluye manual y guía de prácticas, pero su inconveniente es la carencia de portabilidad del hardware empleado y el tiempo considerable necesario para replicar las prácticas. Lo mismo se puede decir del trabajo reportado en (Galliere, 2007). Parent, Hossain, King, Lagua y Gorman (2021) presentan una plataforma experimental similar a la que aquí se reporta, que incluye también videos de apoyo, pero su enfoque es orientado a proyectos finales de ingeniería, no para una asignatura completa, por lo que no incluye un análisis estadístico de sus posibles ventajas.
5. Conclusiones
La evidencia de este y otros trabajos ya citados indica que una población con baja marginación presentaba mayor vulnerabilidad al SARS-CoV-2 pero con una menor brecha digital. La región estudiada mostraba al momento de regresar a actividades presenciales alta vulnerabilidad y tasa de letalidad muy superior a la media en México. Por lo tanto, la decisión de realizar una transición gradual de los estudiantes hacia el aprendizaje híbrido acompañada por el uso de la plataforma experimental y video-tutoriales fue acertada. Además, se confirmó que la plataforma ayuda a incrementar el desempeño de los alumnos. Concluido el tutorial los alumnos mostraron dominio, tanto del FPAA, como de la plataforma, lo que se facilitó a partir de la correspondencia entre los resultados experimentales, la teoría y los video-tutoriales. La realización rápida de prototipos con el FPAA permite pasar rápidamente de conceptos teóricos a la práctica con poco esfuerzo, lo que facilitó subsanar deficiencias en la adquisición de competencias prácticas. Esta plataforma se ha impartido hasta la fecha a alrededor de 100 alumnos de los programas de Licenciatura en Electrónica y Maestría en Automatización, con resultados satisfactorios. Inclusive se pueden implementar sistemas que por su alta complejidad experimentan renuencia a ser llevados a la práctica, como es el caso de los sistemas de orden fraccionario. La plataforma es, por tanto, también una herramienta para trabajo de investigación. En mayo de 2023, la plataforma reafirmó su eficacia en condiciones de crisis y actividad no presencial de los alumnos al ser utilizada nuevamente durante los eventos del volcán Popocatépetl.
Fuentes de financiamiento
Este trabajo no fue financiado, pero se utilizaron recursos hardware provenientes del proyecto CONACYT 181201.
Declaratoria de conflicto de intereses
Los autores no reportan conflictos de intereses.
Declaratoria de disponibilidad de datos
Los datos necesarios para el análisis estadístico se encuentran en este mismo documento, al igual que el tutorial. Una versión más completa se puede encontrar en https://www.researchgate.net/profile/Carlos-Muniz-Montero.
Referencias
Acuña Michel, L. L., Cuevas Salazar, O., y Angulo Armenta, J. (2022). Disponibilidad y conocimientos tecnológicos de docentes universitarios de matemáticas en tiempos de la covid-19. Apertura, Revista de Universidad de Guadalajara, 14(1), 52-65. http://doi.org/10.32870/Ap.v14n1.2136
AN231E04 Datasheet Rev 1.2, http://www.anadigm.com/_doc/DS231000-U001.pdf
Bisquerra-Alzina, R. (1987). La prueba de Levene para la homogeneidad de varianzas en el BMDP. Revista de Investigación Educativa, 5(9). http://hdl.handle.net/10201/96084
Chen, P., y Luo, Y. (2022) Analytical fractional order PID controller design with Bode’s ideal cut-off filter for PMSM speed servo system, IEEE Transactions on Industrial Electronics, 70(2), 1783-1793. https://doi.org/10.1109/TIE.2022.3158009
Colín-Cervantes, J. D., Sánchez-López, C., Ochoa-Montiel, R; Torres-Muñoz, D.; Hernández-Mejía, C. M.; Sánchez-Gaspariano, L. A. & González-Hernández, H. G. (2021). Rational Approximations of Arbitrary Order: A Survey. Fractal and Fractional, 5(4), 267 https://doi.org/10.3390/fractalfract5040267
Consejo Nacional de Población (2010). Índice de marginación por localidad ٢٠١٠, http://www.conapo.gob.mx/work/models/CONAPO/indices_margina/2010/documentoprincipal/Capitulo01.pdf
Galliere, J.-M. (2007). Programmable Analog Array in control-systems laboratory, 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 1-5, https://doi.org/10.1109/MED.2007.4433749
Hernández, J. A., & Luna, N. R. (s.f.). Laboratorio de electrónica analógica usando arreglos analógicos programables por campo (FPAA). [Tesis de ingeniería]. Universidad Pontificia Bolivariana.
Jamshidi, R., y Milanovic, I. (2022). Building virtual laboratory with simulations, Computer Applications in Engineering Education, 30(2), 483-489. https://doi.org/10.1002/cae.22467
Muñiz-Montero, C.; Sánchez-Gaspariano, L. A.; Sánchez-López, C.; González-Díaz, V. R. & Tlelo-Cuautle, E. (2016). On the electronic realizations of fractional-order phase-lead-lag compensators with OpAmps and FPAAs. En Azar, A., Vaidyanathan, S., Ouannas, A. (eds) Fractional Order Control and Synchronization of Chaotic Systems, Vol. 688 [pp. 101-128], Springer, Cham.
Muñiz-Montero, C.; Muñiz-Montero, I.; Neri-Suárez, M.; Ortiz, A. I. & Guevara, A. I. (2021). Efecto regional del Covid-19 en la Universidad Politécnica de Puebla: movilidad, marginación, vulnerabilidad y brecha digital. Congreso Nacional de Cuerpos Académicos, Investigación y Posgrado, Tula-Tepeji, México.
Muñiz-Montero, C.; Munoz-Pacheco, J. M.; Sánchez-Gaspariano, L. A.; Sánchez-López, C.; Molinar-Solís, J. E. & Chavez-Portillo, M. (2025). Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties, Fractal and Fractional, 9(2), 101. https://doi.org/10.3390/fractalfract9020101
Nako, J., Kaloudi, E., Tsirimokou, G., y Psychalinos, C. (2024) An electronically tunable universal non-integer-order filter structure. 2024 Panhellenic Conference on Electronics & Telecommunications (PACET). Thessaloniki, Greece, 1-4. https://doi.org/10.1109/PACET60398.2024.10497036
Pandiev, I. M. (2012). Realization of low-frequency amplitude modulator and demodulator with FPAAs. Proceedings of the XLVII International Scientific Conference on Information, Communication and Energy Systems and Technologies, Veliko Tarnovo, Bulgaria, 517-520.
Parent, D. W., Hossain, T., King, D., Lagua, P. & Gorman, S. (2021). Conducting undergraduate research activities in a remote environment. 2021 IEEE Frontiers in Education Conference (FIE), Lincoln, NE, USA, 1-5, https://doi.org/10.1109/FIE49875.2021.9637202
Radhamani, D., Kumar, N., y Nizar, M. (2021). What virtual laboratory usage tells us about laboratory skill education pre- and post-COVID-19: Focus on usage, behavior, intention and adoption. Education and Information Technologies, 26, 7477–7495. https://doi.org/10.1007/s10639-021-10583-3
Raman, R., Achuthan, K., Nair, V. K., & Nedungadi, P. (2022). Virtual laboratories: A historical review and bibliometric analysis of the past three decades. Education and Information Technologies, 27(8), 11055–11087. https://doi.org/10.1007/s10639-022-11058-9
Rodicio-García, M. L., Ríos-de-Deus, M. P., Mosquera-González, M. J., & Penado Abilleira, M. (2020). La brecha digital en estudiantes españoles ante la crisis de la Covid-19. Revista Internacional De Educación Para La Justicia Social, 9(3), 103-125. https://doi.org/10.15366/riejs2020.9.3.006
Schmelkes, S., La educación superior ante la pandemia de la COVID-19: El caso de México, Universidades, 71(86), 73–87 (2020). https://doi.org/10.36888/udual.universidades.2020.86.407
Secretaría de Educación Pública (2020). Destaca SEP ante UNESCO acciones sobre prevención contra el COVID-19 en México. Gobierno de México. Boletín 68, https://bit.ly/3L5NvQB
SEDESOL, Secretaría de Desarrollo Social (2013). Catálogo de Localidades de la Secretaría de Desarrollo Social, http://www.microrregiones.gob.mx/catloc/Default.aspx
Suárez Lastra, M., Valdés González, C., Galindo Pérez, M. C., Salvador Guzmán, L. E., Ruiz Rivera, N., Alcántara-Ayala, I., López Cervantes, M., Rosales Tapia, A. R., Lee Alardin, W., Benítez Pérez, H., Juárez Gutiérrez, M. del C., Bringas López, O. A., Oropeza Orozco, O., Peralta Higuera, A., & Garnica-Peña, R. J. (2020). Índice de vulnerabilidad ante el COVID-19 en México. Investigaciones Geográficas, (104). https://doi.org/10.14350/rig.60140
UNESCO (2020). Education: From disruption to recovery. https://en.unesco.org/covid19/educationresponse
Villela, F., y Contreras Islas, D. (2021). La brecha digital como una nueva capa de vulnerabilidad que afecta el acceso a la educación en México. Academia y Virtualidad, 14, 169–187. https://doi.org/10.18359/ravi.5395