Introducción
La seguridad de la información y la protección de datos sensibles se han convertido en cuestiones críticas en el mundo digital actual. En este contexto, la criptografía desempeña un papel fundamental al proporcionar una capa de seguridad que garantiza la confidencialidad y la integridad de la información. La esencia de la criptografía radica en su capacidad para encriptar y desencriptar datos de manera eficiente y segura esto se ha vuelto esencial para salvaguardar la privacidad y asegurar que la información sensible no caiga en manos no autorizadas (Biddle et al., 2021). A lo largo de la historia, la criptografía ha evolucionado constantemente, y una de las innovaciones más destacadas en este campo ha sido el uso de curvas elípticas como base para algoritmos criptográficos. Sin embargo, el desafío radica en encontrar un equilibrio entre la seguridad y la eficiencia (Madariaga, n.d.).
La importancia de este problema se encuentra en la necesidad de proteger los datos en un mundo digital cada vez más interconectado. La información confidencial se transmite y almacena en una variedad de dispositivos y plataformas, y es vital garantizar que permanezca inaccesible para cualquiera que no tenga la autorización adecuada (Fúster et al., 2001). La eficiencia se vuelve aún más crucial en este contexto, ya que la seguridad no debe imponer una carga innecesaria en los recursos computacionales limitados (Chávez & Henríquez, 2021).
Las curvas elípticas, que tienen sus raíces en las matemáticas puras, han demostrado ser una herramienta poderosa en el diseño de sistemas de seguridad cibernética avanzados. Su origen se encuentra en la teoría de números y la geometría algebraica, y su aplicación en criptografía se ha vuelto cada vez más relevante en las últimas décadas debido a su eficiencia en el uso de recursos computacionales. Esta eficiencia es crucial en un mundo en el que el almacenamiento y el tiempo de ejecución son recursos limitados y valiosos (Johnson et al., 2021).
Sin embargo, a medida que las curvas elípticas se han consolidado como una base sólida para la criptografía moderna, también ha surgido una creciente necesidad de optimizar aún más la eficiencia de los algoritmos basados en ellas. Esto se debe a que, en entornos donde los recursos son escasos o costosos, como dispositivos móviles o sistemas embebidos, la eficiencia en el almacenamiento y el tiempo de ejecución es esencial para garantizar una seguridad efectiva sin sacrificar el rendimiento (Barbosa Camilo et al., 2011).
En el campo de la criptografía de curvas elípticas, no existe una controversia significativa sobre la eficacia de esta técnica en términos de seguridad. Sin embargo, existe un debate constante sobre cómo mejorar aún más la eficiencia en el almacenamiento y el tiempo de ejecución.
Por lo tanto, el objetivo principal de este trabajo es abordar esta necesidad imperante de eficiencia en la criptografía de curvas elípticas. Presentaremos un algoritmo diseñado específicamente para mejorar la eficiencia en el almacenamiento y el tiempo de ejecución en aplicaciones de seguridad de la información. A medida que avanzamos en la discusión de este algoritmo, exploraremos su diseño, metodología y resultados clave, resaltando su contribución a la optimización de recursos en sistemas de seguridad.
1. Metodología
1.1. Generación de Llaves con Curvas Elípticas
La generación segura de llaves es un componente crítico en cualquier sistema de seguridad de la información, y en el contexto de la criptografía de curvas elípticas, este proceso se basa en principios matemáticos sólidos. A continuación, se detalla la metodología utilizada para generar llaves de manera segura mediante el uso de curvas elípticas:
1.1.1. Selección de los Parámetros
La ecuación de una curva elíptica en forma simplificada es:
|
$$ y^{2}=x^{3}+ax+b $$ |
Esta ecuación es una representación de las curvas elípticas que se utilizan en criptografía. Estas curvas son objetos matemáticos definidos en un plano coordenado, donde cada punto $(x,y)$ en la curva satisface la ecuación anterior (Trappe & Washington, 2006). La razón detrás de esta ecuación es que las curvas elípticas tienen ciertas propiedades matemáticas que las hacen adecuadas para su uso en criptografía. En particular, estas curvas son grupos algebraicos Abelianos, lo que significa que se pueden realizar operaciones de suma y resta de puntos en la curva de una manera coherente y eficiente (Abhishek & Prakash Raj, 2021). Esto es fundamental para algoritmos criptográficos, como el intercambio de llaves Diffie-Hellman y la firma digital (Colliard Schneider & Maris Vaira, 2019).
El uso de un número primo grande en la generación de llaves se relaciona con la seguridad de estos sistemas criptográficos basados en curvas elípticas. La elección de un número primo grande como módulo para las operaciones en el campo finito asegura que el espacio de llaves sea lo suficientemente grande como para que sea computacionalmente inviable realizar ataques de fuerza bruta, donde un atacante probaría todas las llaves posibles hasta encontrar la correcta (Abhishek & Prakash Raj, 2021). Cuanto mayor sea el número primo, mayor será la seguridad del sistema.
El primer paso implica la elección cuidadosa de los parámetros relevantes, que incluyen un número primo grande $p$ que define el campo finito sobre el cual se construye la curva elíptica, así como los coeficientes $a$ y $b$ de la ecuación de la curva elíptica (Trappe & Washington, 2006).
1.1.2. Elección de un Punto Base $G$
Cuando se habla de que un punto base $G$ en una curva elíptica tiene un orden $n$, significa que cuando multiplicamos este punto por $n$ (lo que se conoce como multiplicación escalar), llegamos a un punto que es el elemento neutro de la adición en la curva (generalmente el punto en el infinito). En otras palabras, $n$ es el número mínimo de veces que debemos sumar el punto base $G$ a sí mismo para obtener el punto en el infinito (Trappe & Washington, 2006).
La propiedad de tener un orden $n$ es importante en la criptografía de curvas elípticas porque garantiza que los puntos generados a partir del punto base $G$ sean diversos y no repetitivos, lo que fortalece la seguridad del sistema.
Se selecciona un punto base $G$ en la curva elíptica, que actuará como referencia para la generación de llaves públicas y privadas. Este punto debe tener un orden $n$ lo suficientemente grande y debe ser irreducible en el campo finito (Josias Gbètoho Saho et al., 2020).
1.1.3. Generación de la llave pública y privada
La llave privada $d$ se genera como un número aleatorio dentro del rango $[1,n-1]$, donde $n$ es el orden del punto base $G$. La llave pública $Q$ se obtiene mediante la multiplicación escalar del punto base $G$ por la llave privada $d$.
|
$$ Q=d*G $$ |
2. Encriptación con Curvas Elípticas
La encriptación mediante curvas elípticas es un proceso matemático que utiliza la aritmética modular y las propiedades de la curva elíptica para cifrar datos (W. Li et al., 2021).
2.1. Preparación del Mensaje
En primer lugar, el mensaje original que se desea encriptar debe convertirse en una representación numérica adecuada. En el caso de texto, esto suele implicar la conversión de los caracteres en valores numéricos, como los códigos ASCII de los caracteres. El código ASCII asigna un número entero único a cada carácter o símbolo que puede ser representado en un sistema de computadora. Estos números van desde 0 hasta 127 y se almacenan en 7 bits (Arya & Kumar, 2017). Cada número en el código ASCII corresponde a un carácter específico, como letras, números, signos de puntuación, símbolos matemáticos y de control, así como caracteres especiales.
2.2. Generación de un Valor Aleatorio $k$
Un componente esencial de la encriptación con curvas elípticas es la aleatoriedad. Se selecciona un valor $k$ de forma aleatoria dentro de un rango específico (Trappe & Washington, 2006). Este valor aleatorio se mantendrá en secreto y se utilizará solo para esta operación de encriptación particular.
2.3. Operación de Multiplicación Escalar: $kG$
El siguiente paso implica realizar una operación de multiplicación escalar, donde el punto base $G$ se multiplica por el valor aleatorio $k$ para obtener el punto resultante $C$(Alimoradi et al., 2021). Matemáticamente, se expresa como:
|
$$ C=k*G $$ |
2.4. Cifrado de los Datos $\mathit{Valor}C_{M}$
Considere que se tiene un mensaje $M$ para cifrar sus datos numéricos (por ejemplo, los valores ASCII de un mensaje de texto), se utiliza una función de cifrado que combina $M$ y el punto $C$ en la curva elíptica para obtener un valor cifrado $C_M$
|
$$ C_M= (M+x(C))mod\: p $$ |
Donde $x(C)$ es la coordenada $X$ del punto $C$, y $p$ representa el módulo utilizado en la aritmética modular. La operación de suma se realiza en el campo finito de la curva elíptica (J. Li & Gao, 2022).
El valor cifrado $C_M$ junto con el valor aleatorio $k$ se envía al destinatario. La seguridad del cifrado radica en la dificultad de desencriptar el valor $C_M$ sin conocer el valor aleatorio $k$.
3. Desencriptar con Curvas Elípticas
La desencriptación mediante curvas elípticas es un proceso que implica la inversión de las operaciones realizadas durante la encriptación. Para desencriptar el valor $C_M$, el receptor utiliza el valor aleatorio $k$ y realiza una operación de desencriptación específica (Alhayani et al., 2022).
|
$$ M=(C_{M}-x(C))mod\:p $$ |
3.1. Recuperación del Mensaje Original y Conversión a Texto Plano
El valor $M$ obtenido representa el mensaje original en su forma numérica, como los valores $ASCII$ de los caracteres. Para obtener el mensaje en su formato de texto original, el receptor puede convertir los valores numéricos $M$ en caracteres de texto utilizando la correspondencia del código $ASCII$.
Como se muestra en el $Algoritmo1$, el procedimiento RaizCuadradaMod recibe dos argumentos, $y2$ y $p$, el objetivo es encontrar un número $x$ tal que $x^{2}=y2(mod\:p)$. Esto significa que se busca un valor $x$ para el cual el cuadrado de $x$ dividido por $p$ deje como residuo a $y2$. Para lograr esto, se utiliza la función $(y2)^{\frac{1}{2}}mod\: p$ para intentar encontrar una raíz cuadrada de $y2$ bajo el módulo $p$.
Si se encuentra una raíz cuadrada (es decir, si la raíz no es nula), se verifica si el cuadrado de la raíz módulo $p$ es igual a $y2$. Si es así, la raíz se agrega a la lista de raíces, luego, se calcula el valor negativo de la raíz módulo $p$ (esto se hace restando la raíz de $p$, y se repite el proceso de verificación y adición a la lista de raíces, finalmente, si la lista de raíces no está vacía, se devuelve la primera raíz encontrada, de lo contrario, se devuelve Nulo.
|
Algoritmo 1: Cálculo de la Raíz Cuadrada en Módulo $p$ |
|
RaizCuadradaMod (y2, p) Entrada: $y2$, $p$ Salida: Raíz cuadrada de $y2$módulo$p$ o Null Iniciar lista vacía de raíces
|
El $Algoritmo2$ corresponde al procedimiento CodificarCaracter para codificar un carácter $ASCII$ en sus coordenadas correspondientes en una curva elíptica. El algoritmo entra en un ciclo (pasos 3-8) con la finalidad de obtener las coordenadas $(x,y)$ sobre la curva elíptica generando la codificación del carácter. Con el valor $ASCII$ del carácter el algoritmo calcula la abscisa $x$ así como la ordenada $y$ validando a través de aplicar el residuo de Legendre, este cálculo se realiza para diferentes valores $x$ hasta encontrar un punto válido en la curva (pasos 3-5). Si encuentra un punto válido, el algoritmo devuelve las coordenadas $(x,y)$; de lo contrario, continúa la búsqueda incrementando el valor de $j$ en cada iteración (pasos 6-8).
Considere que $mensaje=Fernando123$, la codificación utiliza los códigos $ASCII$ de los caracteres en el mensaje para obtener como resultado una secuencia de puntos en la curva elíptica. Como resultado de la ejecución del procedimiento CodificarCaracter(mensaje) se obtiene los siguientes puntos en la curva elíptica:
|
$$ \begin{matrix} \left\{ \left\{ 57263,245925 \right\}\left\{ 82623,421674 \right\}\left\{ 93254,412653 \right\}\left\{ 89983,182930 \right\}\left\{ 79348,33448 \right\} \\ \left\{ 89983,182930 \right\}\left\{ 81801,144226 \right\}\left\{ 90799,375650 \right\}\left\{ 40083,274758 \right\}\left\{ 40901,448639 \right\}\\ \left\{ 41720,284598 \right\}\right\}\end{matrix} $$ |
|
Algoritmo 2: Codificación de Caracteres a Coordenadas de Puntos en una Curva Elíptica |
|
CodificarCaracter (mensaje, a, b, p, h) Entrada: mensaje, a, b, p, h Salida: Coordenadas $(x,y)$ en la curva elíptica
|
El siguiente paso en la metodología es generar las llaves públicas para Bob y Alice en función de sus llaves privadas, que ya hemos definido. Para lograr esto, tres algoritmos importantes operan en puntos de la curva elíptica:
- $Algoritmo3$: Suma de Puntos en una Curva Elíptica
- $Algoritmo4$: Duplicación de Puntos en una Curva Elíptica
- $Algoritmo5$: Multiplicación Escalar de un Punto en una Curva Elíptica
El $Algoritmo3$ realiza la suma de dos puntos sobre una curva elíptica, el procedimiento $SumaPuntos$ recibe tres parámetros de entrada el módulo primo $p$, las coordenadas de los $puntoP)(x1,y1)$ y $puntoQ=(x2,y2)$ que se van a sumar. El resultado es la coordenada del $puntoR=(x3,y3)$ correspondiente al resultado de la operación de adición de puntos en la curva elíptica.
|
Algoritmo 3: Suma de dos Puntos en una Curva Elíptica |
|
SumaPuntos (p, puntoP, puntoQ) Entrada: número primo p, $PuntosP=\left\{ x1,y1 \right\}$ y $Q=\left\{ x2,y2 \right\}$ Salida: Punto $R=\left\{ x3,y3 \right\}$
|
El algoritmo 3 $SumaPuntos$ toma tres parámetros de entrada: $P$ y $Q$ son los puntos que se van a sumar, y $p$ es el módulo primo. El resultado es el punto $R=\left\{ x3,y3 \right\}$ que representa el resultado de la adición de $P$ y $Q$.
|
$$ \begin{matrix} \left\{ \left\{ 8612,177796 \right\}, \left\{ 12424,5390 \right\},\left\{ 14023,44715 \right\},\left\{ 13531,127010 \right\}\left\{ 11936,218659 \right\}, \\ \left\{ 13531,127010 \right\}, \left\{ 12301,106504 \right\},\left\{ 13656,120110 \right\},\left\{ 6031,27781 \right\},\left\{ 6152,153375 \right\},\\ \left\{ 6277,138955 \right\} \right\} \end{matrix}$$ |
El $Algoritmo4$ duplica un punto en una curva elíptica. El procedimiento DuplicarPunto recibe tres parámetros de entrada: el módulo primo $p$, el coeficiente $a$ de la curva elíptica y las coordenadas del $puntoP=(x,y)$ que se va a duplicar. El resultado es la coordenada del punto $puntoP=(x3,y3)$ correspondiente al resultado de la operación de adición del $puntoP$ consigo mismo en la curva elíptica.
|
Algoritmo 4: Duplicación de un Punto en una Curva Elíptica |
|
DuplicarPunto(p, a, puntoP) Entrada: $p,a,puntoP=(x,y)$ Salida: Resultado de la duplicación del punto en la curva elíptica
|
El $Algoritmo5$ realiza la generación de llave pública a través de la suma de un punto  veces lo cual representa la multiplicación de un escalar
veces lo cual representa la multiplicación de un escalar  con un punto en una curva elíptica. El procedimiento GeneracionLlavePublica requiere de cinco parámetros de entrada: el módulo primo $p$ y el coeficiente $a$ de la curva elíptica, el punto base $G$ y el valor escalar $k$. El resultado es la generación de la llave pública, que es el resultado de la multiplicación escalar del punto base $G$ con su respectiva llave privada.
con un punto en una curva elíptica. El procedimiento GeneracionLlavePublica requiere de cinco parámetros de entrada: el módulo primo $p$ y el coeficiente $a$ de la curva elíptica, el punto base $G$ y el valor escalar $k$. El resultado es la generación de la llave pública, que es el resultado de la multiplicación escalar del punto base $G$ con su respectiva llave privada.
|
Algoritmo 5: Generación de llave Publica |
|
GeneracionLlavePublica (p, a, G, k) Entrada: $p,a,G,k,Llave \: Privada$ Salida: Llave pública
|
En la Figura 1 podemos apreciar el resultado de estos algoritmos en la generación de llaves públicas de Alice y Bob.
Figura 1
Llaves públicas y privadas de Alice y Bob
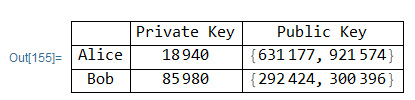
Nota. Elaboración propia.
El $Algoritmo6$ realizar la Encriptación de un Punto en una Curva Elíptica utilizando la llave pública de Bob. El procedimiento Cifrado requiere como parámetros de entrada las coordenadas $(x,y)$ de un punto en la curva elíptica y el valor modular primo $p$ para realizar el encriptado del $punto(x,y)$. En la figura 2 se muestra el resultado que genera este algoritmo donde podemos observar la encriptación del $punto(x,y)$4 en la curva elíptica utilizando la llave pública de Bob y el valor aleatorio $k$.
Figura 2
Asignación de coordenadas y el valor aleatorio k
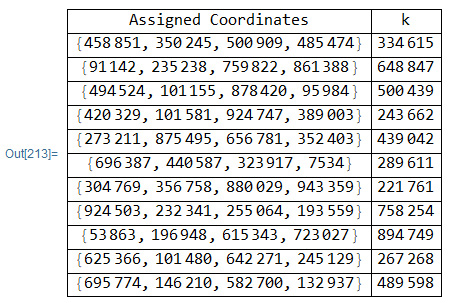
Nota: Elaboración propia.
|
Algoritmo 6: Cifrado de un punto en la curva elíptica |
|
$Cifrado(punto,p,a,G,k,LlavePrivada)$ Entrada: $punto)(x,y),p$ Salida: El cifrado del punto en la curva elíptica usando la llave pública de Bob
|
El $Algoritmo7$ descifra una lista de puntos que fueron previamente encriptados utilizando una multiplicación escalar. El procedimiento Descifrado recibe como parámetro el mensaje cifrado $msgCifrado$ que es una lista de puntos encriptados junto con el valor aleatorio correspondiente $k$ y la LlavePrivada a quien fue enviado el mensaje. El resultado es la lista de puntos descifrados.
|
$$ \begin{matrix} \left\{ \left\{ 454175,47080 \right\},\left\{ 196963,472817 \right\},\left\{ 261813,73676 \right\},\left\{ 454375,13648 \right\},\\ \left\{ 149267,451680 \right\}, \left\{ 320345,23424 \right\},\left\{ 69343,326801 \right\},\left\{ 407006,38689 \right\},\\ \left\{ 358318,196810 \right\},\left\{ 269721,447528 \right\}, \left\{ 234191,439951 \right\}\right\}\end{matrix} $$ |
|
Algoritmo 7: Descifrado de un punto en la curva elíptica |
|
Descifrar(msgCifrado, k, LlavePrivada, p, a) Entrada: Mensaje cifrado, valor de k y la llave privada Salida: Puntos descifrados
|
El $Algoritmo8$ se utiliza para negar la coordenada Y de una lista de puntos y seleccionar un subconjunto de puntos en función de sus coordenadas. Toma dos parámetros de entrada: la lista de puntos (points list) y la lista de puntos2 (points list2). El resultado es la lista de puntos con la coordenada Y negada (DenyPoints2) y un subconjunto de puntos (points1) seleccionado en función de sus coordenadas.
|
$$ \begin{matrix}\left\{ \right\} \left\{ \left\{ 318193,-606787 \right\}, \left\{ 563180,-412611 \right\}, \left\{ 858158,-494470 \right\}\left\{ 351017, -947954 \right\}, \\ \left\{ 450409,-468671 \right\}, \left\{ 427758,-486086 \right\}, \left\{ 276651,-353333 \right\}\\ \left\{ 223934,-313575 \right\},\left\{ 847023,-113099 \right\},\left\{ 223432,-681631\right\}, \left\{ 905960,-89841 \right\}\right\}\end{matrix} $$ |
Los algoritmos empleados en la criptografía con curvas elípticas se basan en el estado del arte: la operación de adición de puntos definida por Koblitz (1987), las técnicas de cifrado basadas en la multiplicación escalar de puntos, el proceso de descifrado el cual sigue el enfoque tradicional de inversión de la operación de cifrado utilizando la llave privada.
La contribución en estos algoritmos fue la implementación en el lenguaje de programación funcional Mathematica® debido al paradigma funcional y simbólico que utiliza para la elaboración de prototipos computacionales. Así como, el diseño de los algoritmos para garantizar un funcionamiento optimizado del proceso, con la finalidad de ofrecer un mejor desempeño computacional en tiempo de procesamiento y almacenamiento de las llaves e información generada sin comprometer la seguridad.
4. Resultados y Discusión
En esta sección, presentamos los resultados para la generación de llaves, cifrado y descifrado, junto con el álgebra desarrollada para las curvas elípticas. Para comprender mejor su aplicación, consideremos un escenario inicial donde se establecen varios parámetros clave:
Número Primo Grande $p$: De manera aleatoria se genera un valor primo grande $p$, para nuestro caso $p=948581$. Este número se utiliza para definir el campo finito sobre el cual construimos la curva elíptica.
Coeficientes de la Curva Elíptica $a$ y $b$: Los coeficientes $a$ y $b$ de la ecuación de la curva elíptica, $y^2=x^3+ax+b$, que cumplen con el determinante $4a^3+27b^2\neq0$ son $85018$ y $7858$, respectivamente.
Punto Generador$G$: Tenemos un punto generador $G$ para la curva elíptica, con las coordenadas {906413,590846}.
Llaves Privadas: Alice posee una llave privada denominada $keySB$ con un valor de 18940, mientras que Bob tiene su llave privada, llamada $keySB$, con un valor de 85980. Ambas llaves son números aleatorios que se encuentran entre 1 y $p$.
Pruebas de Rendimiento: Para llevar a cabo una prueba experimental de los algoritmos para analizar el rendimiento, hemos seleccionado diferentes fragmentos de un cuento. Estos fragmentos varían en tamaño, tomando 100, 650, 1300, 1950 y 2600 caracteres del texto. En estas pruebas experimentales se registró el tiempo de ejecución de los algoritmos de cifrado y descifrado, relacionandolo con el espacio de almacenamiento del texto.
A continuación, se muestra en la Tabla 1 y la Figura 3 un resumen de los resultados de las pruebas en términos de tiempo de ejecución para las operaciones de cifrado y descifrado, así como el espacio de almacenamiento utilizado para cada tamaño de fragmento de texto:
Tabla 1
Resultados de tiempo y almacenamiento
|
Número de caracteres |
Tiempo de Ejecución ( |
Almacenamiento ( |
||
|
Cifrado |
Descifrado |
Texto plano |
Texto Cifrado |
|
|
100 |
0.111709 |
0.0637211 |
103 |
4,328 |
|
650 |
0.845711 |
0.367182 |
663 |
28,216 |
|
1300 |
1.51056 |
0.799223 |
1,327 |
56,432 |
|
1950 |
2.13254 |
1.0682 |
1,999 |
84,728 |
|
2600 |
2.69175 |
1.41516 |
2,662 |
113,000 |
|
3250 |
3.21832 |
1.65021 |
3,333 |
141,274 |
|
3900 |
3.82563 |
1.93796 |
3,997 |
169,312 |
|
4550 |
4.38426 |
2.25774 |
4,661 |
197,572 |
|
5200 |
5.1316 |
2.79604 |
5,333 |
225,795 |
|
5850 |
5.8079 |
2.97587 |
5,999 |
254,160 |
Nota: Elaboración propia
Figura 3
Tiempo de Ejecución de Cifrado y Descifrado
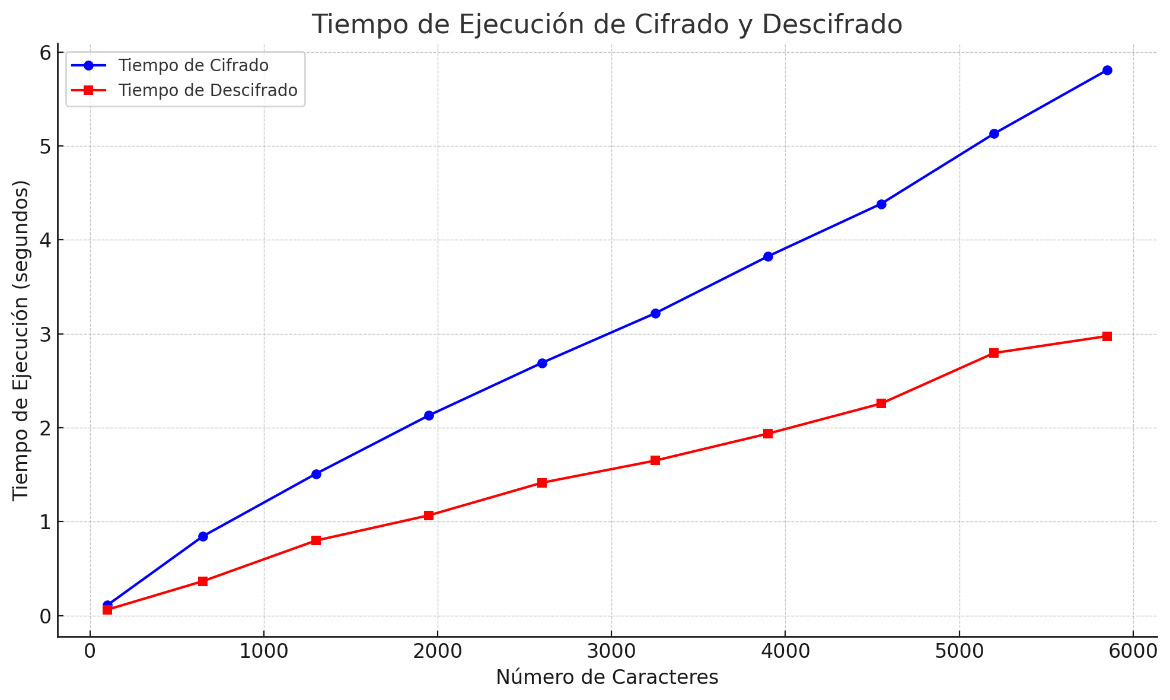
Nota: Elaboración propia
En los datos obtenidos de las pruebas de rendimiento para las operaciones de cifrado y descifrado, se presenta un resumen en la Tabla 1 que refleja el tiempo de ejecución en segundos para diferentes tamaños de fragmentos de texto. La complejidad de las operaciones criptográficas se evidencia a través de estos resultados, ofreciendo una visión del desempeño del algoritmo en relación con el número de caracteres procesados.
Al analizar el tiempo de ejecución para las operaciones de cifrado, se observa un crecimiento proporcional al tamaño del fragmento de texto. En el caso de 100 caracteres, el tiempo de ejecución es de 0.111709 segundos, y este valor aumenta gradualmente a medida que el número de caracteres se incrementa. Este comportamiento sugiere una complejidad que puede describirse mediante la notación $O(n)^2$, indicando una relación lineal entre el tiempo de ejecución y la cantidad de datos de entrada. El orden de crecimiento del tiempo de ejecución de un algoritmo es una característica de la eficiencia del algoritmo y permite compara el rendimiento relativo de algoritmos alternativos.
En cuanto a las operaciones de descifrado, se presenta un patrón similar. El tiempo de ejecución para el descifrado también muestra un crecimiento proporcional al tamaño del fragmento de texto, indicando una complejidad que sigue una relación lineal. Este fenómeno es coherente con la naturaleza de las operaciones criptográficas y la influencia directa del tamaño de los datos en el tiempo de procesamiento.
Figura 4
Almacenamiento de Texto Plano y Cifrado
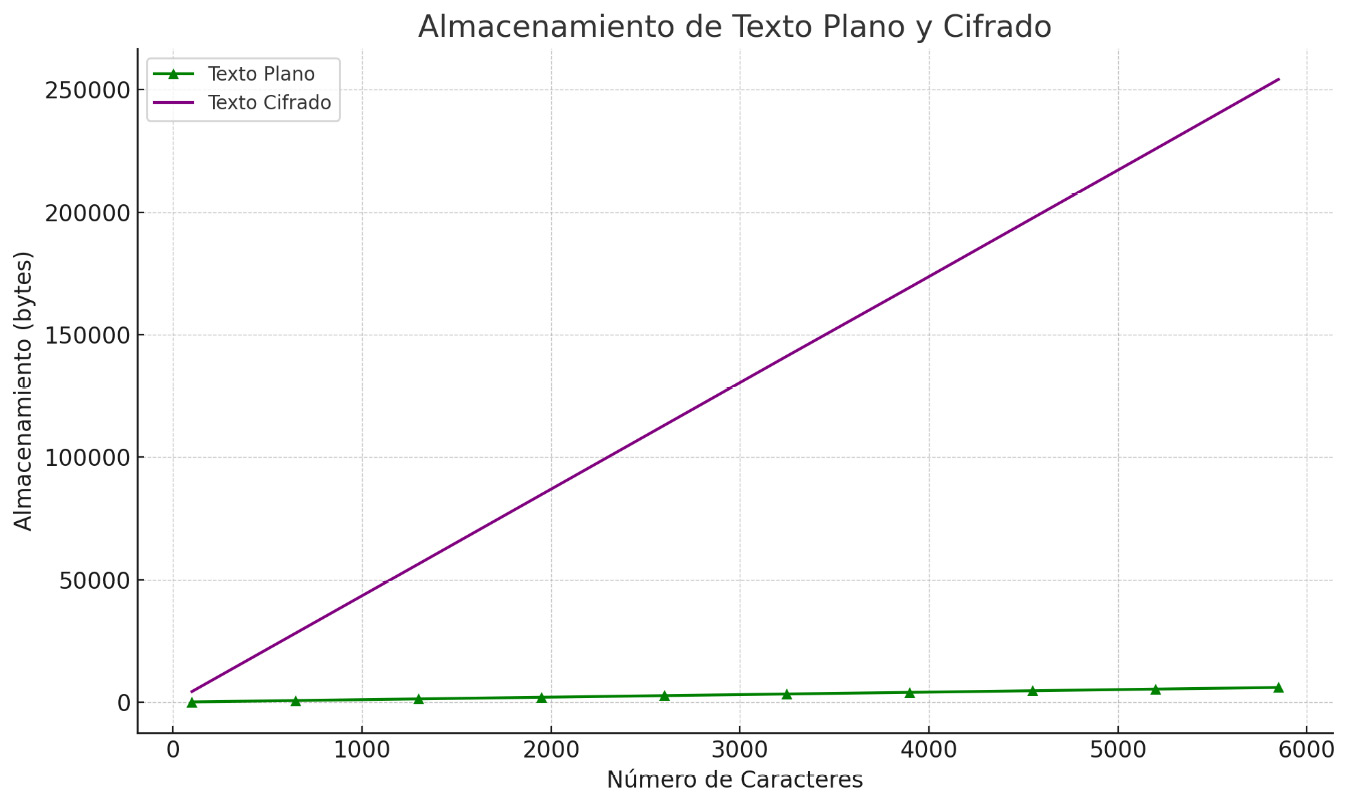
Nota: Elaboración propia
En cuanto al almacenamiento cifrado, se observa un aumento en el espacio necesario para almacenar la versión cifrada del texto (en bytes) a medida que la longitud del texto plano aumenta. Este comportamiento es previsible y común en muchos algoritmos de cifrado, donde el tamaño de la salida cifrada tiende a ser mayor que el del texto plano. Es fundamental destacar que las coordenadas en la curva elíptica constituyen el texto cifrado resultante, lo cual agrega un nivel adicional de seguridad al proceso.
La ventaja distintiva de utilizar Curvas Elípticas Criptográficas (ECC, por sus siglas en inglés) radica en su capacidad para ofrecer niveles de seguridad robustos.
Por otro lado, el aumento gradual en el espacio requerido para almacenar la versión cifrada del texto podría considerarse un desafío. Sin embargo, este incremento en el almacenamiento cifrado se presenta como un indicador positivo desde la perspectiva de la seguridad en la Criptografía de Curvas Elípticas.
Es crucial señalar que la eficiencia de las curvas elípticas en relación con el almacenamiento no se enfoca únicamente en el cifrado y descifrado, sino más bien en la gestión de llaves.
5. Conclusión
En este trabajo se ha abordado de manera efectiva el desafío crucial de mejorar la eficiencia en el tiempo de ejecución en la Criptografía de Curvas Elípticas (ECC). A través de la implementación de un algoritmo específicamente diseñado con funciones matemáticas en Mathematica®, se han aplicado las propiedades de las curvas elípticas en la generación de llaves, así como en los procesos de codificación y decodificación de datos.
Los resultados obtenidos demuestra en términos del tiempo de ejecución. La complejidad de las operaciones criptográficas se ha analizado detalladamente, revelando una relación lineal entre el tiempo de ejecución y la cantidad de datos de entrada, lo que sugiere una eficiencia consistente y escalable del algoritmo.
Además, al examinar el espacio de almacenamiento cifrado, se ha observado un crecimiento esperado en el tamaño de salida cifrada a medida que aumenta la longitud del texto plano. Cabe destacar que el texto cifrado resultante son las coordenadas en la curva elíptica, añadiendo así un nivel adicional de seguridad al proceso.
En este contexto, la Criptografía de Curvas Elípticas se posiciona como una solución efectiva para abordar los desafíos del rendimiento en sistemas de seguridad de la información. La capacidad de ECC para proporcionar niveles robustos de seguridad con una demanda reducida de recursos computacionales refuerza su relevancia y aplicabilidad en entornos donde la eficiencia es esencial. (Alhayani et al., 2022).
Referencias
Abhishek, K., & Prakash Raj, E. G. D. (2021). Computation of Trusted Short Weierstrass Elliptic Curves for Cryptography. 21(2), 71–88.
Alhayani, B. S. A., Hamid, N., Almukhtar, F. H., Alkawak, O. A., Mahajan, H. B., Kwekha-Rashid, A. S., İlhan, H., Marhoon, H. A., Mohammed, H. J., Chaloob, I. Z., & Alkhayyat, A. (2022). Optimized video internet of things using elliptic curve cryptography-based encryption and decryption. Computers and Electrical Engineering, 101. https://doi.org/10.1016/j.compeleceng.2022.108022
Alimoradi, R., Arkian, H. R., Razavian, S. M. J., & Ramzi, A. (2021). Scalar multiplication in elliptic curve libraries. Journal of Discrete Mathematical Sciences and Cryptography, 24(3). https://doi.org/10.1080/09720529.2017.1378411
Arya, E. S., & Kumar, A. (2017). Ascii Based Encryption Decryption Technique for Information Security and Communication. 3rd International Conference on Innovative Trends in Science, Engineering and Management, YMCA Connaught Place, New Delhi, 7th January.
Barbosa Camilo, Castang Gerardo, & Tibaquira Yesid. (2011). Implementación del criptosistema de curva elíptica en entornos móviles. VINCULOS, 8. https://doi.org/10.14483/2322939X.4198
Biddle, G., McGoldrick, L., & Halamek, J. (2021). Non-traditional encryption methods: Moving toward electrochemical cryptography. Electrochemical Science Advances, 1–7. https://doi.org/10.1002/elsa.202100188
Chávez, M. A. L., & Henríquez, F. R. (2021). Post-Quantum Digital Signature for the Mexican Digital Invoices by Internet. Computacion y Sistemas, 25(4). https://doi.org/10.13053/CyS-25-4-4048
Colliard Schneider, C. D., & Maris Vaira, S. (2019). Protocolos Criptográficos Basados en los Algoritmos de Diffie-Hellman y RSA.
Fúster, A., Guía, D. de la, & Hernandez, L. (2001). Técnicas criptográficas de protección de datos. México.
Johnson, D., Menezes, A., & Vanstone, S. (2021). The Elliptic Curve Digital Signature Algorithm (ECDSA).
Josias Gbètoho Saho, N., Ezin, E. C., Josias Saho, N. G., Ezin, -Eugène C, Watson, B., Badouel, Er., & Niang, O. (2020). Comparative Study on the Performance of Elliptic Curve Cryptography Algorithms with Cryptography through RSA Algorithm. https://hal.science/hal-02926106
Li, J., & Gao, W. (2022). Hardware Optimization and System Design of Elliptic Curve Encryption Algorithm Based on FPGA. Journal of Sensors, 2022. https://doi.org/10.1155/2022/9074524
Li, W., Chang, X., Yan, A., & Zhang, H. (2021). Asymmetric multiple image elliptic curve cryptography. Optics and Lasers in Engineering, 136. https://doi.org/10.1016/j.optlaseng.2020.106319
Madariaga, A. P. (n.d.). Curvas Elípticas y Criptografía.
Trappe, W., & Washington, L. C. (2006). Introduction to Cryptography with Coding Theory (2nd ed.). Pearson Education. Inc., Ed.


