ESTIMACION DEL PRECIO DE UN TITULO OPCIONAL MEDIANTE UNA RED NEURONAL ARTIFICIAL

Guillermo Pérez Ellzalde Egresado de la Escuela de lngenierta Universidad L a Salle

y Eduardo Gómez. RdrnírE-z.

Laboratorio de Investigación y Desarrollo de Tecnolog1a Ava izada LIDETEA

Posgrado e Investigación. Universidad La Salle Benjamín Franklin No 4 Col. Condesa

CP 06140 Mex1co, O.F, Mex1co E-mail:egornez@aldeha1an .c1 ulsa.mx

RESUMEN

Títulos Opcionales (TO's) es la denominación que las autoridades del Mercado Mexicano de Valores le dieron a los instrumentos que internacionalmente se denominan "Warrants". Uno de los modelos más utilizados para la valuación de estos instrumentos es el propuesto por Black & Scholes. el cual

es utilizado en la Bolsa Mexicana de Valores (BMV) para el cálculo del precio teórico de los TO's.

En este trabajo se presenta el diseño de un modelo de Red Neuronal Artificial (RNA) para estimar el precio de cierre de un Titulo Opcional (TO). Para demostrar la potencialidad de estimación de la RNA se realizan análisis de regresión y de varianza. por un lado entre los precios de cierre y la estimación del modelo de Black & Scholes (B&S), y por 01ro lado entre los precios de cierre y la estimación hecha por la RNA.

ABSTRACT

Títulos Opcionales (TO's) is the name thal the Mexican Stock Market authorities have given to the financíal instruments thal have been internationally called Warrants. The model proposed by Black & Scholes is one of the most widely used models for valuing these financia! instruments and which is used by the Mexican Stock Exchange (BMV) for calculating the theorical price of the TO's.

The design of a rnodel of an Artificial Neural Network (RNA) for estimating the closing price of a TO is shown in this paper. In order to demonstrate the potential estímate of the RNA, severa! regression and variance analyses are carried out. At first are comparing the closing príces and the estímate calculated by the Black & Scholes model,and then are comparing the closing prices and the estimate calculated by the RNA.

INTRODUCCION

Los TO's pertenecen a una familia de instrumentos financieros llamados productos derivados , los cuales surgen como un mecanismo de cobertura del riesgo an1e la inestabilidad de los mercados y la elevada volatilidad de los precios. La caracteristica principal de estos instrumentos es que su precio está asociado al precio de otro

instrumento financiero al que se denomina activo subyacente.

Recientemente diversos investigadores han observado algunas limitaciones en los modelos financieros que dependen de la distribución normal y/o varianza finita, entre los que se encuentra el

modelo de BlacK & Scholes ( 1973).

Re v C<Jritro l11v (Méx) Vol 3 Nv tn 12 (1999)

Por un lado E. Peters (1) comenta "la naturaleza fractal" 1 de los mercados de capitales contradice la Hipótesis de Mercados Eficientes (HME) y todos los modelos cuantitativos que se derivan de ésta. Esto explica que estos modelos fallan porque simplifican la realidad asumiendo comportamiento aleatorio e ignoran la influencia del tiempo en la toma de decisiones.

Andre Lo {2) refuta la HME y señala que existen

relaciones muy complejas entre los activos finan­ cieros a lo largo de muchos y diferentes puntos en el tiempo.

H. Ahmadi [3] estudia los problemas del

' Un fractales unobjeto en el cuallas partes es1á11 de alguna manera relacionadas hacia un todo.es decir. los componentes 1nd1v1duales son similares entre ellos.

modelo APT (Arbitrage Pricing Theory) usandouna RNA para investigar simultáneamente elefecto de algunas variables sin conocer las distribuciones de probabilidad de cada variable.

Mandelbrot (4), (5}, (6) (mucho más conocido quizá por haber iniciado el estudio de las cuNas fractales en matemáticas) propone que los precios t ienen una distribución de Pareto estable.

Hull [7) propone modelos en los que la desviación estándar de los precios es a su vez volátil.

Herb Johnson & David Shanno [8] comentan: "El modelo de Black & Scholes supone que el precio del activo subyacente sigue el movimiento geométrico browniano. y esto implica que el precio de un activo subyacente tiene una distribución log­ nornal por lo que la tasa de rendimiento es normalmente distribuida". Lo anterior implica que de acuerdo al teorema del 1 ímile central, la distribución de cambios de precios diarios de las acc iones (las cuales son sumas de muchos ca mbios de precios intra-dia) debería ser aproximadamente normal.

Sin embargo, las condiciones del teorema pueden no ser cumplidas debido a:

a) Los cambios de precios pueden no tener una varianza finita [9], [1O].

b) El número de efectos individuales sumados al mismo tiempo para dar el cambio del precio diario puede ser en sí mismo aleatorio (11]. (12) dando origen a procesos subordinados.

Hay también considerable evidencia de que las varianzas cambian sobre el t iempo (13]. [14]. [15], (16].

Por lo anterior es apropiado examinar modelos de valuación de opciones que permitan que la varianza cambie. Los científicos de la Cibernética en su afán por convertir a esta ciencia en una herramienta que auxilie al hombre en el estudio de los sistemas dinámicos complejos que se caracterizan por su comportamiento no lineal. propone analizar el Mercado de Valores como un sistema complejo, dinámico, viable y adaptable. [17]

Las Redes Neuronales Artificiales (RNA) son

modelos matemáticos que poseen las caracterís­ ticas anteriores,cuya potencialidad principales la de aproximar relaciones complejas no lineales.

Una muestra de la motivación para estudiar el Mercado de Valores con el enfoque de la Cibernética son los trabajos de:

a) John Kean [18] en el que comenta que los mercados financieros pueden apreciarse como sistemas dinámicos no­ lineales y las RNA's pueden ser usadas para analizar y medir patrones de comportamiento en la variación de precios.

b) Mayer & Feliz (19] en el que muestran la no presencia de caos pero si la fuerte evidencia de dinámica no lineal de los índices de precios de México (IPC),Nueva York (Oow Janes) y Tokio (Nikey) durante

el periodo que comprende del 12 de Enero de 1986 al 23 de Febrero de 1990.

c) Edgar Peters (1) en el que demuestra la existencia de un atractor caótico para el S&P 500.

d) Herbert A Simon [20) en el que opina que un sistema puede generalment e ser conducido con mas precisión si éste usa alimentación anticipada ("feedfo!Ward") en combinación con retroalimentación para corregir los errores del pasado.

Entre las aplicaciones de RNA's en los mercados de derivados internacionales se encuentran los siguientes:

a) Mary Malliaris & Linda Salchenberger (21) demuestran la habilidad de una RNA para es tima r los precios de una opción financiera.

b} Hutchinson, Lo and Poggio [22) estudian la limitación delmodelo de Black & Scholes y proponen una RNA para la valuación y cobertura de los productos derivados cuando las dinámicas del precio de los activos subyacentes son desconocidas y la ecuación de valuación asociada con la condición de no-arbitraje no puede ser solucionada analíticamente.

e) David L. Kefly (23] muestra la aplicación de una RNA para la valuación y cobertura de opciones de venta.

d) Milliaris & Salchenberger [24) muestran la potencialidad de las RNA para la predic-

"' í :r 1 '11v 1"A I-_ J \/)/.1 " f í r1

ción de la volatilida d implícita de las op­ ciones financieras.

El modelo de B&S supone que la distribución de probabilidad de las cotizaciones futuras del activo subyacente es lag-normal y que la volatilidad del rendimiento de dicho activo es constante. pero esto no siempre se cumple, por lo que es necesario implementar un modelo que tenga la habilidad para capturar la dinámica del activo subyacente con un mínimo de supuestos.

Debido a la necesidad de construir modelos de va luac ión de opciones financieras que permitan que la varianza cambie y dada la potencialidad de las RNA's para aproximar funciones no lineales, en el presente trabajo se formula la siguient e hipótesis. ¿ El empleo de RNA's para la estimación de precios de cierre de los TO's permite obtener mejores resultados que el modelo de B&S ?

El estudio de tecnologías inteligentes y su implantación en nuestro país para el estudio de nuevos mercados financieros adquiere gran importancia no sólo por la necesidad de responder a las exigencias del proceso de globalización financi era en ma teria de innovaciones tecnológicas de instrumentos financieros y de técnicas de análisis de la información, sino también por el hecho de que las comunidades mexicanas académicas e industrial del ramo computacional y financiero puedan participar en la evaluación y aplicación dichas tecnologías.

El presente trabajo representa un esfuerzo en este sentido y tiene como objetivo analizar la problemática de B&S y presentar el desarrollo de una RNA para la est imación de precios de cierre de un TO listado en la BMV como una alternativa de solución,presentando dos casos:

1) Cuando la R NA obtiene mejor es estimaciones que el modelo de B&S.

2) Cuando el modelo de B&S obtiene mejores estimaciones que la RNA.

Este estudio puede ser aplicable a otros instrumentos derivados, activos subyacentes y modelos de valuación de activos financieros que dependen de la distribución normal y/o varianza finita. En particular se sugiere el empleo de una RNA para la estimación de precios de los futuros sobre índices financieros. tipos de cambio y ta-

sas de interés que cotizarán en el Mexder (Mer­ cado Mexicano de Derivados estandarizado) .

El trabajo está estructurado de la siguiente forma:

En la primera secc ión se describen los fundamentos de valuación de los TO's.

En la segunda secc ión se revisan los fundamentos de las RNA's y se desarrolla un simulador del algoritmo de aprendizaje ''backpropaga tion", el cual se utiliza para el entrenamiento y prueba de las RNA's diseñadas en el capítulo cuatro.

En la tercera sección se describe la metodologia de diseño de una RNA y el diseño de una RNA para la estimación de precios de cierre de un TO listado en la BMV

Por último se presentan las conclusiones y trabajo futuro.

FUNDAMENTOS DE VALUACION DE L0S

TITULOS OPCIONALES

Los Títulos Opcionales (TO's) son aquellos documentos suscept ibles de oferta pública y de intermediación en el Mercado de Valores, que confieren a sus tenedores. a cambio del pago de una prima de emisión. el derecho de comprar (Si se trata de un TO de compra) o el derecho de vender al emisor (Si se trata de un TO de venta):

a) Un número de acciones del activo de referencia

b) Un número de acciones de un grupo o canasta de referencia

ó bien de recibir del emisor una determinada suma de dinero resultante de la variación del índice de precios de referencia. a un cierto precio llamado precio de ejercicio y durante un período de tiempo determinado.

De acuerdo al tipo de derecho que otorga el contrato los TO's pueden ser:

a) De Compra (Call): Si el tenedor tiene el de­ recho de comprar.

b) De Venta (E.!.!it Si el tenedor tiene el dere­

cho de venta.

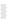Rev c;cntro Jn11 {Mo,¡ Vol .1Nvm 1'2 ¡1 • Y9)

421

De acuerdo al período dentro del cual se puede ejercer el derecho, los TO's pueden ser de tipo:

c} Americano : Es aquel TO que puede ejercerse en cualquier momento anterior a su vencimiento.

d) Europeo: Es aquel TO que puede ejercer­ se sólo en la fecha de su vencimiento. [25]

El precio corriente de mercado de una acción de referencia es el precio actual determinado por la oferta y demanda existente en el mercado secundario en cuestión, por lo que de manera más especifica los TO's de compra otorgan a sus tenedores. el derecho de:

1. Adquirir del emisor las acciones o canasta de referencia; ó

2. Recibir del emisor la suma de dinero que resulte de la difer encia positiva determinada en la fecha de ejercicio, entre el precio corriente de mercado de la acción de referencia o del conjunto de acciones de la canasta de referencia, según sea el caso , y el precio de ejercicio; ó

3. Recibir del emisor la suma de dinero que resulte de la diferencia positiva determinada en la fecha de ejercicio, entre el valor de mercado del indice de referencia expresado en términos monetarios y el precio de ejercicio.

y los TO's de venta otorgan a sus tenedores el derecho de:

1. Vender al emisor las acciones o canasta de referencia; ó

2. Recibir del emisor la suma de dinero que resulte de la diferencia positiva determinada en la fecha de ejercicio, entre el precio de ejercicio y el precio corriente de mercado de la acción de referencia o del conjunto de acciones de la canasta de referencia según sea el caso; ó

3. Recibir del emisor la suma de dinero que resulte de la diferencia positiva determinada en la fecha de ejercicio, entre

elprecio de ejercicio y el valor de mercado del índice de referencia expresado en términos monetarios.

En caso de que el precio corriente de merca­ do se muestre en contra de las expectativas del tenedor y éste no ejercite el derecho que le otorgó un TO, entonces perderá la prima que pagó por un TO. (26]

Con el objeto de facilitar la explicación del manejo de los TO's,en lo sucesivo se citará como activo subyacente cuando se trate de una acción de referencia ó canasta de acciones de referencia ó indice de precios de referencia.

Al combinar los dos tipos de contratos (compra.venta) y las dos posiciones que pueden tomar las partes contratantes (tenedor,emisor) da como resultado las siguientes cuatro posibles transacciones que se pueden realizar con los TO's.

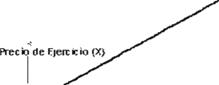
a) Comprar un TO de compra: Posición larga en un TO de compra (Fig. 1}, es decir adquirir el derecho de comprar el act ivo subyacente a un cierto precio (X) a cambio del pago de una prima (C).

Gananc1-a

28 -

24 1

20 l

16

12

8

4

o +.+tt-1-1-ttt H-+t-H-T1-tt::;.rfi-t-t-t+++-H-+t-H-TTf'1'1H+!-t-ttttt

-4 ......,....,,....,........,.......,....,...,,..,.,..,.,f :

-8

Hg. 1 Posición larga en LJrl TO d0 compra

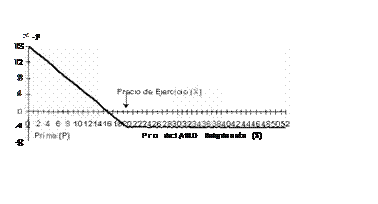
b ) Comprar un TO de venta : Posición larga en un TO de venta (Fig. 2), es decir adquirir el derecho de vender el activo subyacente a un cierto precio (X), a cambio del pago de una prima (P).

R<1v. ('1;11tm lnv (Afi;•x) VPI J N11111. 12 ( 199GJ

Al igual que en los activos financieros clási­ cos en las opciones existen dos tipos de valores:

Fig 2 Posición larg.:s en un TO de ve1ita

g Vender un TO de compra: Posición corta en un TO de compra (Fig. 3), es decir adquirir el compromiso de vender el activo subyacente a un cierto precio (X). a cambio del cobro de una prima (C).

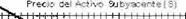
F19. 3 Po:·1c1ón corta en un 1O de compra

d) Vender un TO de venta: Posición corta en un TO de venta (Fig. 4), es decir adquirir el compromiso de comprar el activo subyacente a un cierto precio (X), a cambio del cobro de una prima (P).

a) Valor de mercado (VM): Es el precio corriente de mercado. Si existe una oferta importante el precio de las TO's bajará, mientras que si la demanda es la elevada el precio de los TO's subirá.

b) Valor teórico (VTO)· Es determinado por una serie de parámetros que desde un punto de vista teórico influyen de manera decisiva en el valor del TO en cuestión.

Ambos valores pueden coincidir si el mercado secundario de TO's se comporta de manera eficiente, es decir si sus precios reflejan toda la información relevante para la formación de expectativas, en cuyo caso el VTO será su precio de mercado.

En el caso de que el mercado sea ineficiente existirá una desviación entre el VTO y el VM del TO y el signo nos indicará si está sobrevalorado o infravalorado por el mercado. de ahí la importan­ cia de conocer el valor teórico de un TO.

El VTO puede definirse como:

VTO = VI + VT ( Ec. 1)

Donde VI es el valor intrínseco y representa el beneficio inmediato que el comprador del TO puede obtener a través del ejercicio del TO. Puede expresarse como la .diferencia entre el precio del activo subyacente(S) y el precio de ejercicio del TO (X).

3

& Prmo('P)

4

2

o +,;-.,.....,_.,...,..,,.,...,... ...,..,=....,=.c,..,.,...,..,...i-+-,-,

==== ;·

rrrr-=1

Para el caso de un TO de compra:

VI = MAX(O, S-X) ( Ec. 2 )

Para el caso de un TO de venta:

J 1 Precio del AclivoSub)'atenre(S)

: · Precio de f jen;icio(X)

-14

·16 -X

Fig. 4 Posición cona en un TO de venta

La elección de alguna de ellas dependerá de las expectativas que el inversionista tenga sobre la evolución del precio del activo subyacente y del riesgo que qwera asumir. {27]

Ri3v. Csntm lnv (1'i, 1é. ! Vol 3 Num 12 {1999)

Donde VT es el valor tiempo y representa las expectativas de los inversionistas en TO's, las cuales en el caso de un comprador de un TO de compra serán alcistas. en el caso de un comprador de un TO de venta serán bajistas.

En función del valor intrínseco las TO's se pueden clasificar en tres categorías.

423

a) Dentro de Dinero (ITM. I n the Monevl.Son aquellos cuyo valor intrínseco es positivo, esto es:

Para el caso de un TO de compra S>X

Para el caso de un TO de venta X>S

b) En el Dinero (ATM. Al ! he Money): Son aquellos cuyo precio de ejercicio es igual al precio del activo subyacente por lo que su valor intrínseco es cero,esto es:

Para el caso de un TO de compra S=X

Para el caso de u n TO de venta X=S

e) Fuera de Dinero (OTM, Out of the Money): Son aquellos que en términos analíticos su ejercicio implica una pérdida, por lo que su valor intrínseco es cero. esto es:

Para el caso de un TO de compra S<X Para el caso de un TO de venta X<S

Los TO's OTM sólo tienen VT, por lo que tan­ to el emisor como el tenedor sólo consideran la evolución favorable de los precios del activo subyacente. Los TO's ITM son los que tienen el menor VT.

Los TO's ATM son los que tienen el máximo VT, ya que cuando se valora un TO asumimos que el mercado es eficiente, es decir que los precios reflejan plenamente toda la información relevante del correspondiente activo, bajo este supuesto la mejor estimación del precio futuro sería el precio actual y los precios tendrían una distribución

normal, tal como se presenta en la Fig. 5.

En la Fig. 5 el área marcada con SD'X repre­ senta la probabilidad de que S>X, es decir cuan­

do un TO de compra este ITM existe una probabi­ lidad de aproximadamente el 50% de obtener be­ neficios en su ejercicio.

En la Fig. 6 se muestra como en un TO ITM existen probabilidades de ganar más VI (área marcada con SüX), pero también existe la posibi­

lidad de perder parte del valor intrinseco actual con una evolución desfavorable de los precios (área marcada con XCJS) por lo que siempre el VT de un TO ITM será inferior al VT de un TO ATM .

-·

=1

1 .I

, _

..J

1

F1g 6 Otstnb·.cion de probablf1dr.1d da 105 precios

del activo suby.,,canto:-:

(TO ITM)

El caso de un TO OTM se muestra en la Fig. 7,en la cual se observa como el área marcada con XDS es inferior a la correspondiente marcada con

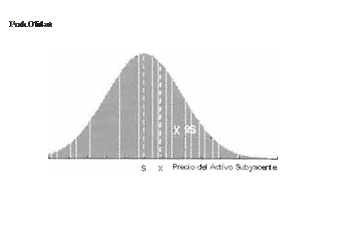
SD X de la Fig. 5, es decir su VT es inferior al de un TO ITM.

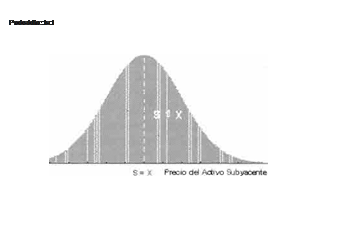
Fig. 5 01stnbuc1or: ele probab1ltdad de los precio

dF MC'1vo subyacente .

TO ATM)

F1 7 Disllibuc1on de probabllidatJ de los precios di:ll activo subyacente

( TO OTM )

Para los TO's de venta se puede observar cómo cuando un TO comienza a estar ITM el VT

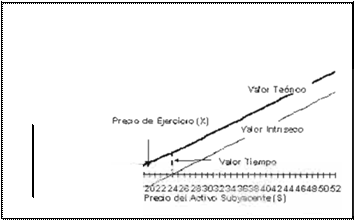
de la TO se anula. Esto se debe a que en el caso de los TO's de venta europeas. el valor tiempo puede llegar a ser negativo. En las Figs. 8 y 9 se muestra la evolución del VTO,del VI y del VT en función al precio del activo subyacente.

:t

'H 0< r.,¿,,co fC)

n -

29 !

1

t

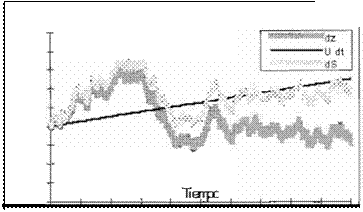
F1g 1O Mov1m1cfllO geométnco brnwriiano

16

12

a

4

o -m-.,..,.,...."T""""""l'4"'....,_.-,..,.........,.....

·• ,¡....., ,_,....,.,,.....,..,....., .....:·

·S

Firy 8 C•:)n1riortarni 'llv d 1 Véllor teór ico d un

TO d ' co1np1a

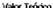
'"ºk

::1 -·-'"

4 VdlYl.-..í"""° ll!ldodeijElddo(Y.J

V T tEIYOO 1

o 1;-t-t-t-1 1 1 1 1 1 1 1 1 ...,.........,.......,.....,.::::;:,;:;,::,:1;::,;:;1::+1!:¡:1;:=1<:¡:¡¡::¡¡: :ii o "'"'""i"i'.,,..·'"'""1

2 4 6 8 10121416:ra 2022 2426 28 30 32 34 36 38 40 <Q"4 46 4HO $2

-8

F g 9 Cor.ipor1arri1--:nto d-1 valo1 t,.,011c:o d un

TO (1_ vent

Si S es la variable en cuestión entonces su pro­ ceso de ito es:

dS = µSd1 + CYSdz

Para la valuación de los TO's la BMV en la nota metodológica del boletín bursátil "Sección Análisis y Valuación de instrumentos del Mercado de C apitale s" establece que el pre cio del subyacente es el precio actualizado para la valuación del mercado accionario.

El modeliJ dE: Black & Scholes.

El modelo de Fisher Black & Myron Scholes publicado en 1973 fue concebido inicialmente para valuar opciones europeas sobre acciones de tipo europeo.

Las hipótesis básicas del modelo son:

1. Mercado financiero perfecto. en el sentido de que los inversionistas pueden pedir prestados los recursos monetarios que necesiten, sin limitación alguna, a la vez que prestar sus excedentes de liquidez al mismo tipode interés sin riesgo, el cual es conocido y se considera constante en el período estimado.

2. Inexistencia de costos de transacción y de información.

3. Ausencia de impuestos.

4. No consideración del dividendo que pueda recibir la acción,durante el período de vida de la opción.

5. Se trata de un mercado de negociación

continua.

d S =µd1 + a d z

s

( Ec. 4 )

6. La distribución de probabilidad de las cotizaciones futura s de las a cciones es

El proceso más habitualpara describir la evo­

lución del precio de una acción o de una divisa es el llamado "Movimiento geométrico brownjano'' (Fig. 10)

logarítmico-normal y la varianza (volatilidad) del

rendimiento de las acciones es constante por unidad de tiempo del período.

Este modelo descansa sobre el principio de la formación de una cartera sin riesgo, compuesta por opciones europeas sobre acciones y por las

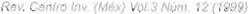4 2 'i

acciones que constituyen el activo subyacente de dichas opciones.

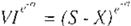Según la formula de la Ec. 2, el valor actual del VI referido al momento t en el cual se adquiere una opción de compra y utilizando la fórmula de descuento en el campo continuo sería:

( Ec. 5 )

donde:

S = Precio del activo subyacente

X = Precio de ejercicio de la opción

r = Tasa de interés

(! = 2.7182818

Según la formula anterior se puede afirmar que el VTO en el tiempo t es igual a la diferencia entre el valor del activo subyacente y el precio de ejercicio de la opción traído a valor presente.

Con elfin de reflejar la incertidumbre que existe de que la opción tenga VI. la fórmula de Black & Scholes incorpora las probabilidades de que se tenga VI.

De manera que si no queremos correr riesgos, sea cual sea la variación en el precio de la acción,la proporción entre acciones poseídas y opciones emitidas debe ser h, ya que el resultado positivo o negativo de la opción se compensa con el resultado positivo o negativo de la acción. La rentabilidad de la cartera será independiente de los cambios en los precios de la acción.

Si suponemos que el precio de la acción es una variable aleatoria en el campo cont inuo, que sigue una distribución de probabilidad logarítmico-normal con una media y una varianza constantes, el riesgo es también nulo cuando se ajusta continuamente la posición de cobertura h.

Bajo este supues to fue de finida la siguiente fórmula de valoración de opciones de compr a ( C) y opciones de venta (P) de tipo europeo que no paga dividendos.

-n

C = SN(d1 )- Xe N(d2 ) ( Ec. 7 )

11

P = Xe - N( -d 2)- SN( -d1 ) ( Ec. 8 )

siendo:

Ln (t)+(r +f2) t

A simismo. para eliminar el riesgo

asociado a los efectos del cambio de precio de las acciones, Black & Scholes proponen en su modelo la formación de una cartera formada por la combinación adecuada de una posición larga en acciones y una posición corta en opciones emitidas sobre tales acciones .

donde:

d , =

a. Ji ( Ec. 9 )

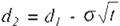( Ec. 10)

426

,

Si conside ramos un sólo período y simbolizamos por p la probabilidad de aumento del precio de la acción a S1 y por 1-p la probabilidad de baja del precio de la acción a S2

y por c1 y e? el precio de la opción de compra

como consecuencia del aumento o disminución del precio de la acción, al cual se refiere la opción de compra. al cociente entre la variación de precio de la opción de compra y la variación del precio de la acción se denomina "hedge ratio" (h) y se expresa de la siguiente manera.

h = C1 - C2

51 - S2 ( Ec. 6 )

C Valor de una opción de compra

p ::=. Valor de una opción de venta

S = Precio del activo subyacente

X Precio del ejercicio de la opción

N(rl ) ) y

Nrd2 J Funciones de densidad de las variables . d, y d1

N Distribución normal acumulativa

r Tasa de interés libre de riesgo

= Tiempo que falta hasta el vencimiento de la opción

CJ Volatilidad del activo subyacente

Re" Cer.t,.o /nv (AMx> Vol 3 Num. 12 (1999)

Para el caso en el cual el a ctivo subyacente si paga dividendos continuos la for­ mula de valoración de opciones de compra y opciones de venta de tipo europeo es :(28)

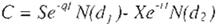( Ec. 11 )

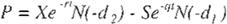( Ec. 12)

Dicha señal es enviada a través de los canales de comunicación unidireccionales a otras unidades de la red, en estos canales la señal se modifica de acuerdo con la sinapsis w. asociada a

J'

cada uno de ellos según una determinada regla

de aprendizaje. Las señales moduladas que han llegado a la unidadj-ésima se combinan entre ellas generando así la entrada total Nett

síendo:

_ Ln ( ) +(r - q + f ) 1

Net 1 · = "L(.",;'

-V' w1 ·

) ( Ec . 15 )

d , - ,- ( Ec. 13)

<J , / f

d 2 == d 1 - ª"''Í¡ ( Ec. 14 )

donde:

q= Tasa anualizada de rendimientos por dividendos

FUNDAMENTOS DE REDES NEURONALES ARTIFICIALES

Las RNA's son modelos matemáticos que se han desarrollado para estudiar la mente y la actividad cerebral.

Hecht- Nielsen define formalmente una RNA como una estructura de procesamiento paralelo distribuido de información, constituida por unidades de proceso (UP). los cuales están interconec t ados con señales de canal unidireccional llamadas conexiones. Cada UP tiene una conexión de salida simple que se ramifica en muchas conexiones colaterales en la medida que se desee.

La señal de salida de cada UP puede ser de algún tipo de señal matemática. El procesamiento que ocurre dentro de cada UPdebe ser completamente local y puede depender únicamente de los valores comunes de la señal de entrada que llegan a la UP por la vía de sus

conexiones y de los valores almacenados en los

Una función de activación F determina el

nuevo estado de activación ai(t+1) de la neurona considerando la entrada total calculada y el ante­ rior estado de activación a1(t).

Una unidad de proceso también referenciado como: nodo, unidad de memoria a corto plazo, neurona y unidad lógica de umbral, es el componente de una RNA en donde se lleva a cabo el proceso de computación. Sí se tienen N unidades es posible designar la j-ésima unidad como Uj. Generalmente se pueden encontrar tres tipos de neuronas.

1. Unidades de entrada: Reciben estímulos externos (información) relacionadas con el aparato sensorial y constituyen la capa de entrada.

2. Unidades ocultas: Procesan la información de

entrada y generan un tipo de representación interna de la información, constituyendo lo que se conoce como capa oculta o intermedia.

3. Unidades de salida: Dan la respuesta del

sistema y constituyen la capa de salida.

Entre las neuronas que forman una RNA existe un conjunto de conexiones que unen unas con otras Cada unidad transmite señales a aquellas que están conectadas con su salida. Asociada con la unidad U1 existe una función de salida fí(ai(t)) que transforma el estado actual de

activación ai(t) en una señal de salida yi{t); es decir

elementos de procesamiento de memoria local.

y ( t) =f (a (t))

• / l I

( Ec. 16)

1

Cada neurona i-ésima está caracterizada en cualquier instante por un valor numérico denominado estado de activación a (t) asociado a

cada UP, existe una función de salida f. que transforma el estado actual de activación e'n· una

señal de salida y,.

R ev. C entro lnv. (Méx ! Vo l . 3 Nu m 1 2 (199YJ

A menudo es de tipo sigmoídal y suele ser la misma para todas las unidades, pero puede utilizarse también las funciones lineal. mixta y escalón.

En la figura 11 se muestra un modelo típico de una RNA.

427

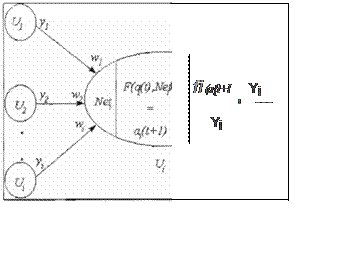
Fig. 11 Modelo tlp1co de una RNA. La RNA 8ackpropagat10 1

En 1986, Rumelhart, Hinton y Williams formalizaron un método conocido como backpropagation (Fig. 12) (propagación del error

hasta que todas las neuronas de Ja RNA hayan recibido un error que describa su aportación relativa al error total. Basándose en el valor del error recibido,se reajustan los pesos de conexión de cada neurona de manera que en la siguiente vez que se presente el mismo patrón la salida esta más cercana a la deseada ; es decir, el error

disminuya.

La importancia de la red backpropagation consiste en su capacidad de autoadaptar los pe­ sos de las neuronas de las capas intermedias para aprender la relación que existe entre un conjunto de patrones dados como ejemplo y sus salidas correspondientes .

Esta característ ica se conoce como generalización y se define como la facilidad de dar salidas satisfactorias a entradas que la RNA no ha visto en su fase de entrenamiento. [29]

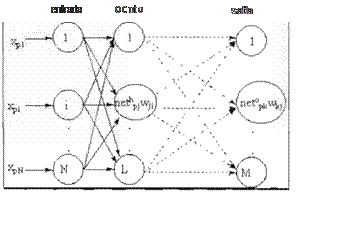hacia a trás) el cual es tá basado en la

generalización de la regla delta y a pesar de sus propias limitaciones, ha ampliado de forma con­ siderable el rango de aplicaciones de las RNA's.

El algoritmo backpropagation es una regla de aprendizaje que se puede aplicar en modelos de RNA's con másde dos capas de neuronas. Una característica importante de este algoritmo es la representación interna del conocimiento que es capaz de organizar en la capa oculta.

t { 81 dé

r.; :- J e l

NIVel de

428

De forma simplificada el funcionamiento de una RNA backpropagation consiste en un aprendizaje de un conjunto predefinido de pares de entradas-salidas dados como ejemplos, empleando un ciclo de propagación-adaptación de dos fases.

Primero se aplica un patrón de entrada como estímulo para la capa de entrada, después se va propagando a través de todas las capas superiores hasta generar una salida, se compara el resultado obtenido en la capa de salida con la salida que se desea obtener y se calcula un valor de error para cada neurona de salida.

A continuación estos errores se transmiten hacia atrás partiendo de la capa de salida hacia todas las neuronas de la capa intermedia que contribuyen directamente a la salida, recibiendo el porcentaje de error aproximado a la participación de la neurona intermedia en la salida original.

Este proceso se repite capa por capa,

Ftg. 12 Modelo de arqu1tPctura de una RNA Back-propagal1on

DISEÑO DE UNA RED NEURONAL ARTIFICIAL PARA LA FSTIMACION DE PRECIOS DE UN TITULO OPCIONAL

1. Definición del problema

El modelo de Black & Scholes supone que el valor de mercado de un activo financiero sigue el Movimiento geométri co browniano en tiem­ po continuo, según la Ec. 2.18. El Movimiento geométrico browniano es un proceso de lto en el que S es la variable en cuestión.

Elproceso de lto es una generalización del pro­ ceso de Wieoer. Un proceso de Wiener es un proceso estocástico en elquela función de den­ sidad de probabilidad de la variable aleatoria es una distribución normal.

Rev Cen1ro /1 v (McJ Vol Num 12 1 1999)

Dado que una variable I Qgnormal puede asu­ mir sólo valores positivos,se aplica el groceso a una variable lognormal para represen­

tar los precios de los activos financieros . La distribución de probabilidad de las cotizacio­ nes futuras de un a ctivo financiero es logaritmico-normal.

La tasa de rendimiento es normalmente distri­ buida y la varianza del rendimiento del activo financiero es constante por unidad de tiempo.

De acuerdo al teorema del limite central si te­ nemos una sucesiónde variables independien­

tes x1. xz, x3.... xn con la misma distribución de

probabilidad, la misma media y la misma varianza, entonces la sucesión de variables

aleatorias z,. zz. z .... Z • definida como:

3 11

z = Y,, - .U x ( Ec. 17)

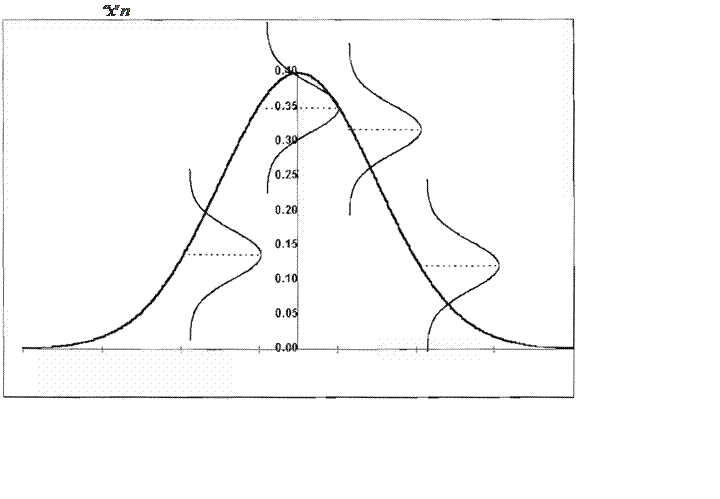n r

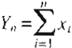( Ec. 18)

tiende a la distribución normal estándar cuando

n tiende a infinito.

Aplicando el teorema del limite central a una variable que sigue un proceso de Wiener nos encontramos que:Toda variable definida como la suma de n variable s normales

independientes Z,. es a su vez una variable normal cuya varianza es la suma de las varianzas de todas las Z; y cuya media es la

suma de las medias de todas las Z Lo ante- rior implica que la distribución de prec'·os diarios

es normal, y que la tasa de rendimiento son sumas de muchos cambios de precios intra­ dia, como se muestra en la Fíg. 13.

Fig. 13'

Aplicac1on del teorema del !Imite central a una variable que sigue un proceso je W1ener

Las condiciones del teorema del límite central pueden no ser cumplidas debido a:

a) Los cambios de precios pueden no tener una varianza finita [9], [1O].

b) Elconsenso es que las distribuciones son

extremo esbeltas y por lo tanto no normales, sin embargo, distribuciones estables con varianza infinita noajustan los datos tan bien como mesco lanzas de normales con diferentes varianza.

e) Existe evidencia de que las varianzas

Rev CA11/ro /nv (M(; x i V ol 3 fllvr¡: l'i ;l':!!J<l)

cambian sobre eltiempo (13]. [14]. [15], (16].

d. Aplicar término (a-b)/(a+b)

El modelo de B&S está limitado a que la dinámica delactivo subyacente siga un proceso de Wiener (distribución normal) y esto puede no suceder, por lo que es necesario

f (X, ), = (X r - X 1 _ 1 )

( X , + X 1 • 1 )

( Ec. 22)

implementar un modelo que tenga la habilidad para capturar la dinámica del activo subyacente con un mínimo de supuestos.

a)

VARIABLE DESCRIPCION T-t = Tiempa que falta hasta el vencimiento de la opción. S/X = Cociente de S entre X S/Xlt-1) = Cociente de S entre X en (t-1) S/X(t-2) = Cociente de S entre X en (t-2) C(t-1) = Precio del Título Opcional en t-1 Clt-21= Precio del Título Oocional en t-2 AB* = Valor correspondiente al término (a-b)/(a+b)

Selección de var iables de entrada

e. Concatenar resultados de el y e

4. Selección de muestras de entrenamiento y prueba

213 del total -> Muestra de Entrenamiento

1/3 del total -> Muestra de Prueba

5. Definición de topología.

Nivel de Nodo Tipa de entrada aceotada Decimal Función de Transferencia Siamoide Nivel de Red Número de nodos en Capa de Entrada 13 Número de capas ocultas 3 Número de nodos en cada capa oculta 13 Número de nodos en la capa de salida 1 Nivel de Entrenamiento Algoritmo de Aprendizaje Regla Delta Generalizada Parámetros de aprendizaje Beta = 0.9 Alfa = O N.F.= O Error = 0.000001

* = Este término se aplica a las 6 variables de entrada y la variable de salida, por lo que en total se tienen 13 variables de entrada.

b) Variable de salida

C Precio del Título Opcional

2. Recolección de información

Para la recolección de información se realizó un análisis sobre la distribución de frecuencias de los activos financieros utilizados como valor subyacente. Losactivos financieros más utilizados como valor subyacente fueron CEMEX BCP, TELMEX L y el IPC, los cuales ocupan respectivamente el 18.5%, 16.8%, 16.8%.

3. Preprocesamiento de información

a Calcular 01ferenc1as

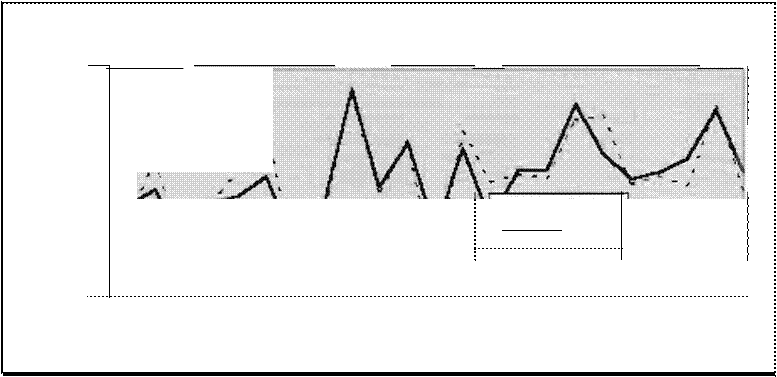
Como se puede observar en la Fig. 14 la serie (RNA) estimada por la red casi está montada sobre la serie (C) que representa los precios de cierre, lo cual nos indica que la RNA pudo reconocer la función de (C) con un alto grado de aproximación, que se confirma en la Fig. 15 en la que la serie estimada por la RNA sigue a la serie

b

c.

43(1

f (X,), =X,- X 1 _ ,

N< r a iza Rango

f ( X , J , = (X, -µ ,)

a

Aplicar L1nciór sigrno1de

)

J

( X ) -- ­

, ' - ( 1 + e·')

( Ec. 19)

( Ec . 20)

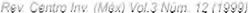( E c . 21)

(Real) con mucho mayor precisión que la serie B&S.

En la tabla 1 se puede observar cómo el coeficiente correlación, MAPE y promedio de los cuadrados de los residuos aplicados a la serie Real vs. RNA tienen un mejor desempeño que los indicadores aplicados a la serie Real vs. B&S.

6. Fase de Entrenamiento ( RNA que SI aprendió)

	Inicio	Fin
Entrena	21/02/95	17/07/95
Prueba	18/07/95	4/09195
Iteraciones	10034
Beta	0.9
Alfa	o
N F.	o
Error	1E-07

7.

T S/X S/X (t-1) S/X (t-2) C(t-1) C(t-2) e T 1.000 S/X -0.935 1.000 S/X (t-1) -0.93C 0.984 1.000 SIX (t-2 -0.920 0.964 0.983 1.000 C(t-1) -0.867 0.958 0 978 0.963 1.000 C(t-2) -0.854 0.927 0.955 0.97 0.968 1000 e · 0.875 0.978 0.964 0.944 0.971 0.936 1.000

Fase de Prueba. ( RNA que SI aprendió)

D esemp efio de la RNA CMX509A durante fase d e PRU EBA

1

1

0.9

0.8

07 ..

I l

08 "

0.5

0.4 - - - e

0.3

0.2

0 .1

'º

o

., RNA

1() L() 1() 1() lO IO lO lO 1() I(') 1() LO 1() \(") 1() lO lO 1() 1() lü IO LO 1()

,.... ,.... "" ,.... ,.... ,....

Q? Q.! Q? ! Q? '<:! Q? Q? Q? '<:! Q? Z! Q?

t t-. t-. co 00 00 ro ro 00 00 00 e.o O:• •:O w O) e;,

Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q

N N N N N (') ('"¡ o C• o

o .- (') co °' o (')

00 a..o (f'} 1() ú) ,.... o ,.... ,.... ('°} 00 o.....

,.... ,....

.- N N N N ('l N N (') o o

Fig. 14 Desempeno de una RNA que SIaprend10

1 1;1v Cen t10 ln v . cMex ) \/o l .3 Num 12 ( 1999 )

431

10JJO

O OJ

B (0

7 OJ

Comparación de precios Aeo B&S y RNA

-·

8.Q)

---Real

---B&S

- • Prqe10 RNA

5.0J l---.....---.... ---.- ,...--.....---.----,. -.-- ........ .....-.

---. -.--....... -....---1

l ' # ' . ? p " . j ? # '? $'" i " # # "' if-" # ' <3>-{?- , # "' <!> ., 1 l' i ,

# 4 # ef , $

Fig 1 '> Comparación de prec!os (RNA que SI aprerid!O)

8 Validación del desempeño de la RNA. ( RNA que SI aprendió)

Resljmen estadístico precio real VS precio B&S CMX509A DC031

rES T ADIST/CAS-DE REGRESION- - - - - - -, [= = L Coeficiente @..CQlfflÍACW !Jl{i/1.iBJL _Q_7as2354Q.!L _J M.M'_I 0.07J16473a Coeficiente de determinación R " 2 0.622892624 R" 2 ajustado 0.595956383 Error típico 0.806134591 ObseTVacione s 16

ANAL/SIS D E VAR IANZA

Grados de Suma de Promedio de F Valor crítico libertad cuadrados /os cuadrados de F

Regresión 1 1502765829 r15.02765829 -, 23.12470479 0.000277923 Residuos 14 9.097941706 L0. 649852979 _J Total 15 24.1256

Resumen Est a dístico Precio R eal VS Precio RNA CMX509A DC031

ESTADl$TICAS DE REGRESION [coeficiente de correlación mú.!!!Ple LJ .980971047J r - - - - u-- - - L _ _ _MAPL 0.02534888[ Coeficiente de determinación R"2 0.962.304 196 R"2 ajustado 0.959611638 Error tipico 0.254871662 Observaciones 16

ANÁLISIS DE VARIANZA

Grados de Suma de Promedio de F Valor crWco llbertad cuadrado s los cuad rados de F

Regresión 1 23.21616611 r23.21616611i 357 3941192 2 3039E-11 Residuos 14 0.909433894 L0.064959564_J Total 15 24.1256

Tablo 1 Estadísticas de RNA que (SI aprendio)

Rev Gemrc fnv , 1vl'! 1 11 0 1 J Num. 12 (''.?99i

En la Fig. 16 se puede observar que la serie (RNA) no sigue un comportamiento similar a la serie (C). y la Fig. 17 confirma el no aprendizaje de la RNA.

En la tabla 2 se puede observar que aun cuando los indicadores favorecen al análisis Real vs RNA estos no

son significativos.

9 Fase de Entrenamiento ( RNA que NO aprendió )

10 Fase de Prueba. ( RNA que NO aprendió)

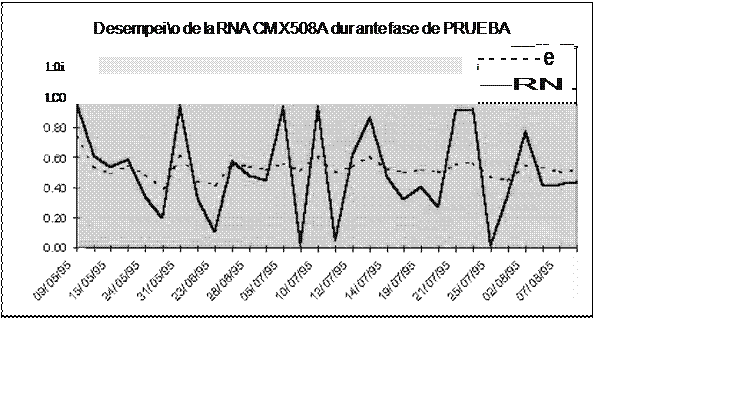
Fig.16 Desempeno de una RNA que NO aprendió

R ev Centro inv (Mé>.J Vol 3 Núm 12 (1999) 43J

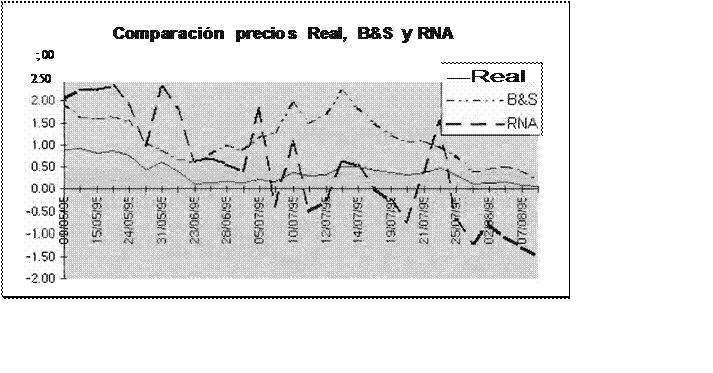
Flg. 17 Comparac1on de precios (RNA que NO aprendióJ

11 Validación del desempeño de la RNA. ( RNA que NO aprendió)

Resumen estadístico precio real VS precio B&S CMX508A DC024

[ coeficiente de correlación múltiple 0.68066503 [= = = ESTAOISTICAS DE REGRESION MAPE 1 2 96340990 Coeficiente de determinación R" 2 o 463304896 R"' 2 ajustado 0.444137213 Error típico 0.189997051 Observ<iciones 30

ANAL/SIS DE VARIANZA

Grados de Suma de Promedio de F Valor crítico libertad cuadrados los cuadrados de F Regresión 1 o 872551376 0.872551376 24.171149 3 48547E-05 Residuos 28 1.010768624 r ---;;i L0.03609887 Total 29 1.88332

Resumen Estadístico Precio Real VS Precio RNA CMX509A DC024

[coeficiente de correlación múltiple .767039768] [= ==MAP4 79927963 ESTADJSTICAS DE REGRESION Coeficiente de determinación R"2 0.588350006 R"2 ajustado 0.57364822 Error tfplco 0.166397616 Observaciones 30 ANÁLISIS DE VARIANZA

Grados de Suma de Promedio de F Valor crítico libertad cuadrados /os cuadrados de F

Regresión 1 1.108051333 1 108051333 40.018949 7.64591E-07 Residuos 28 0.775268667 [o 027688167] Total 29 1.88332

Tabla 2 Esladisucas de RNA que NO aprendió

43 4

Rev. Cen1r o lnv ( Mf!x ) Vof 3 N u m 12 (1999 )

} \,

r

Por lo anterior se concluye que el empleo de RNA's para la estimación de precios de cierre de los TO's permite obtener mejores estimaciones que el modelo de B&S para el caso de un TO de compra ITM, no siendo así para el caso ATM.

12. Extracción de reglas

Será en una segunda fase de este proyecto en donde se profundizará en eltema de extracción de reglas, ya que se tiene proyectado la integración de un sistema experto con la RNA en donde la RNA encuentre las reglas del sistema experto.

13. Implantación del modelo

El tiempo de cómputo de la RNA fue mucho mayor en comparación al cálculo realizado con el modelo de B&S, sin embargo, el tiempo y el costo de una RNA será menor conforme la RNA esté mejor entrenada y se podrán obtener estimaciones con mayor precisión en comparación a las estimaciones obtenidas con el modelo de B&S, lo cual se verá reflejado en las utilidades de los portafolios de inversión que contengan TO's.

CONCLUSIONES

1. El empleo de RNA's para la estimación de precios de cierre de los TO's permite obtener mejores estimaciones que el modelo de B&S para el caso de un TO de compra ITM, no siendo así para el caso ATM.

2. Es posible mejorar el desempeño de la RNA para los casos ATM y OTM diseñando nuevos modelos con otras :

a) Emisiones de TO's

b) Variables de entrada

c) Técnicas de preprocesamiento de información d} Estrategias de entrenamiento

e) Topologías

f) Algoritmos de aprendizaje

3. El desempeño mostrado por la RNA para la estimación correcta de precios de cierre permite sugerir el desarrollo de una interfaz que alimente a la RNA de precios del activo subyacente en tiempo real [30). con el objeto de obtener indicadores de compra o venta durante la operación del mercado.

Rev C e niro Jnv { Mex) Vol J Núm . 1 ¿ ( 1999)

4. . Las capacidades de aprendizaje y adaptabilidad a cambios de los sistemas cibernéticos, permiten sugerir a las RNA's como una herramienta para modelar la volatilidad en el MMPD.

5. Los modelos de valuación de instrumentos financieros juegan un papel determinante en la formación de precios de activos financieros, los cuales a su vez si reflejan toda la información relevante para la formación de expectativa s, determinan la eficiencia o ineficiencia del mercado. Por lo anterior es posible afirmar que et empleo de herramientas cibernéticas para estimación de precios (cuya potencialidad radica en la extracción de información} contribuye a la efciencia de un mercado. [31)

6. Dado que los productos derivados contribuyen a la disminución de la volatilidad de los activos subyacentes, es necesario contar con un método de valuación de los TO's que capture la dinámica del activo subyacente (y no la suponga} para de esta forma contribuir a la eficiencia del mercado mexicano de los activos subyacentes. la cual según el estudio realizado por Pizaña (32] en 1993, es ineficiente .

7. Es de gran importancia que los inversionistas mexicanos conozcan y utilicen herramientas cibernéticas, no sólo por el hecho de contar con una ventaja competitiva regional, sino también por el hecho de que el proceso de globalización financiera exige el dominio de innovaciones tecnológicas en materia de herramientas de análisis de la información.

8. Atendiendo al comentario final [33) "Las instituciones de enseñanza superior deben jugar un papel central en los procesos de evaluación, selección e implementa ción de nuevas tecnologías", este trabajo representa un esfuerzo en la aplicación de nuevas técnicas de análisis de instrumentos financieros listados en el Mercado de Valores Mexicano.

REFERENCIAS

1. Edgar E. Peters (1992) "Chaos and Order in

the Capital Markets" , John Wiley & Sons, lnc. USA.

2. Andrew Lo (1993) "On the path to price predic­ tion", Entrevista Wall Street & Techno/ogy, Junio.

3. Harnid Ahrnadi (1990) "Testability oflhe Arbi­ trage Pricing Theory by Neural Network", Proceed­ ings of the IEEE lntematt0naf Conference on Neu­ ral Networks, pp. 11385-1393, San Diego CA.

4. Mandelbrot, B (1964) "The variation of Certain Speculat1ve Prices''.ln: P. Cootner (ed}. T/1e Ran­ dom Character of Stock Prices Cambridge, MA MIT Press.

5. Mandelbrot, B (1971} . "When can Price be arbitraged efficently ? A Limit to the Validity of the Random Walk and Martingale Models", Review of Economics and Statistics 53.

6. Mandelbrot, B. (1961) "Stable Paretian Ran­ dom Functions and the mult iplicative variat ion of lncome", Econometrica 29.

7. John Hull & Alan White {1987} "The Pricing of Options on Assets with Stochast ic Volatilities". The Journal of Finance, Vol.42 No.2, pp.281-300 ,June.

8. Herb Johnson & David Shanno (1987) "Option Pricing when the variance is Changíng", Journal of Financia/ and QuanlJfative Analysis , Vol 22 No.2. pp 143-151, June

9. Mandelbrot, 8. (1963) "The Variation of Cer­ tain Speculative Prices". Journaf of Business. 36 Oct, pp.394-419.

10. Fama, E. F. (1965) "The Behavíor of Stock Market Prices". Joumal of Business,38 Jan, pp.34- 105.

11. Mandelbrot. B.& H (1967}.Taylor "On the Dis­ tribution of stock price Diferences". Operatíon Re­ search, 15 (Nov/Dec.) pp.1057-1062 .

12. Clark, P.K. (1973) "A subordinated stochastic process model with finile variance for speculative prices". Econometrica. 41 (Jan,) 135-155.

13. Black F.{1975) "Forecasting variance of stock prices for options trading and other purpouses", Seminar on the Analysis of securitiy pric es, Univ. of Chicago (Nov).

14. Blatberg, R.C. & N.J. Gonedes (1974) "A com­ parison of the Stable and Student Dístributions as Statistical models far stock prices", Joumal of Busi­ ness, 47 (April ), pp.244-280 .

15. Chrislie A. A. ( 1982) "The Stochastic behav- 1or of common stock variances : Value, leverage and interest rate effects", Joumal of Financia/ Eco­ nomics. 10 (Dec), pp.407-432.

16. Rosenberg, B. (1972) "The behavior of ran­ dom variables with nonstationary variance and the distribution of security prices". Working Paper, Univ. CA al Berkeley.

17. Felsen J. (1975) "Cybernelic Approach to stock Market Analysis", CDS Publísíng Company, USA.

18. Kean J. (1992) "Chaos Theory and Neural Network Analysis". Technical Analysis of Stocks and Commoditie s, June.

19. David Mayer & RaulAnibal Feliz (1992) "Non­ linear dinamics in the stock Exchange", División de Economía, CIDE, MEXICO.

20. Herbert A. Simon (1996) "The Sciences of the Ar t ificial" , The MIT Press Cambndge , Massachesetts USA.

21. Malliaris M.E. & L. Salchenberger {1993) "Beating the Best: A Neural Network Challenges the Black & Scholes Formula", Proc. of /he Ninlh Conference on Artificial lntelligence for Aplications. Los Alamitos CA. IEEE Computer Society Press. pp.445-449

22. James M. Hutchinson. Andrew W. LO, &

Tomaso Poggio (1994) " A Nonparametric Ap­ proach to Pricing and Hedging Oerivative Securi­ ties Via Learning Nelworks". The Joumal of F1-

nance Vol.49 No.3. July, pp.851-888.

23. David L. Kelly (1994) "Valuing and hedging american put options using Neura/ Networks", Carnie Mellon University and University of Califor­ nia Santa Barbara CA.

24. Malliaris M.E. and L. Satchenberger (1994) "Neural Networks for Predicting Options Volatility". World Congress on Neural Networks, San Diego. CA, June 5-9, pp. 11 290-295

25. Bolsa Mexicana de Valores (1995) "Que son y cómo operan los Títulos Opcionales en México", Limusa Noriega Editores. México.