Un Método de Pertitrbaciones Paramétricas
para Controlar el Circuito de Chua
Hugo Gonzaléz Hernández
RESUMEN
El control de Caos ha sido un área de investigación en expansión en la última década. Se han desarrolla do una gran cantidad de teorías y técnicas
para controlar o suprimir Caos. Algunas de las técnicas más populares son los llamados métodos de perturbación paramétrica. los cuales han sido
derivados del método OGY original (1). Estas técnicas utilizan un parámetro accesible del sistema para ser variado, a fin de estabilizar alguna de las
Órbitas Periódicas Inestables (OPl's) empotradas en el atractor del sis tema. En este trabajo se reporta la aplicación de una extensión del enfoque de
OGY para controlar el cir cuito de Chua. Esta extensión consiste en utilizar el Mapa de Primer Retorno en lugar del Mapa de Poin caré para describir
la dinámica del sistema en la vecindad de una Órbita Periódica Inestable.
Palabras clave:
Caos, control, estabílización.
ABSTRACT
Chaos control has been an expanding research area over the last decade, therefore a great amount of techniques have been developed far controlling or
suppressing chaos . Sorne of the most popular tech niques are !he so-called parametric perturbation methods, which are denved from the original OGY
method (1). These techniques use an accessible system's parameter for being changed in order to stabi lize one of the system's Unstable Periodic
Orbits. In this paper we report the application of an extension from the OGY approach to control chaos in Chua's circuit. This extension consists in
using a First Return Map instead of a Poincaré Map for describing the system's dynamics in the neighborhood of an Unstable Periodic Orb1t.
Keywords
:
chaos. control, stabilization.
INTRODUCCIÓN
En la últi•na década ha habido una gran explosión en el campo de la dinámica no lineal, especialmente concerniente al control de Caos. Esto es debido a
la consideración de que las oscilaciones caóticas son un tipo peculiar de comportamiento irregular e impredecible, co múnrnen¡e considerado
indeseable. Por esto, en la mayoría de los casos se trata de controlar-
lo o evitarlo lo más posible.
A pesar de los esfuerzos por parte de los investigadores en el area para controlar Caos, no se ha podido desarrollar una metodología "unificada" para
el control de Caos. A diferencia de los problemas clásicos de control, donde la estabilización tiene un significado claro, la esta bilización de Caos
puede ser entendida en muchos sentidos diferentes (2). Algunos auto res definen el objetivo de control como la estabi lización de puntos de
equilibrio. la eliminación de cuencas múltiples de atracción, y en algunos
Re
C
e
ntre
l1w (MP
J •101. 4 N11r1. IS 11,¡osto 2000 63
 casos, la estab1hzación de órbitas periódicas inestables. Esto nos lleva a diferentes enfoques de control (3) como los métodos de control de
"rediseño". métodos de perturbaciones para métncas, métodos de fuerza externa y métodos de ingeniería de control.
casos, la estab1hzación de órbitas periódicas inestables. Esto nos lleva a diferentes enfoques de control (3) como los métodos de control de
"rediseño". métodos de perturbaciones para métncas, métodos de fuerza externa y métodos de ingeniería de control.
Los métodos de perturbaciones paramétricas son derivados del método desarrollado por E. Ott, C. Grebogi y J A. Yorke, comúnmente conocido como OGY (
1). Este método está basado en la idea de que un atractor caót ico está compuesto por la cerradura de un número 1níinito de Órbitas Periódicas
Inestables (OPI), y que el sistema se puede estabilizar con
¡:;equeñas perturbaciones de un parámetro accesible del sistema. En general, esto hace que la trayectoria de solución del sistema se vea forzada a
pasar a través de la variedad estable de un punto fi o en un mapa que repre senta la dinámica del sistema en una dimensión menor (4)
Una de las principales características de esta técnica es que puede ser implantada a partir de una sene de tiempo proveniente de mediciones del
sistema. sm necesidad de un conocimiento a priori de las ecuaciones que describen el com portamiento del mismo (5).
SISTEMAS CAÓTICOS
Considere la familia de sistemas dados por la s1gu1ente ecuación.
definiendo un sistema como (1} Denotando el flujo generado por (Ec ) como 4>(l,x), y
suponiendo que /\ e <J\n es un conjunto com pacto invariante baJO Nt,x), /\. se dice caótico si·
i. Sensibilidad a condiciones iniciales. Existe una s: > O tal que, para cualquier x e /\ y cualquier vecindad U de x.
existen y e U y t > D
tales que l<!>(t.x) -cjJ(1,y)I> E .
1i
.
Trans
í
t
i
vidad topo
l
ó
g
i
ca
Para cua lquier par de conjuntos abiertos U, V e /\, existe t e <JI tal que 4>(t, U) n V 0
CONTROL POR MÉTODOS DE PERTURBA CIONES PARAMÉTRIC A.S
En 1990, Ott. Grebogi y Yorke (1) desarrollaron una técnica general para controlar sistemas no lineales estabilizando una OPI empotrada en su atractor
; esta técnica utiliza perturbaciones paramétricas dependientes del tiempo. Esta idea viene de la observación de que un atractor caótico típicamente
tiene empotrado un conjun to denso de OPl's (7). (8).
Si se tiene un sistema como (1) donde {3 es un parámetro del sistema que puede ser sujeto de un ajuste externo en un rango pequeño,{Y f3max <{3<!3"+ L\Omax .con t:i.f3max como la pertur
bación máxima permisible, se puede suponer que para f3 = rr el sistema se comporta de forma
caótica.
.t,
= f (x ,r,B )
(Ec
.
1)
Si representa el vector de coordenadas del Mapa de Poincaré (superficie de sección), entonces ·
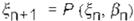
donde x E n es el estado. f · Hv -> CJ¡ n es un
campo vectorial suave, y f3 denota los parámet ros del sistema. La solución de (Ec. 1) es una función vectorial x = x( t) que describe la trayec toria en el espacio construido con sus coorde nadas. Dependiendo de los valores de los pará metros, el
sistema puede desplegar diferentes estados estacionarios que van desde puntos de equilibrio hasta atractores caóticos.
Definición 1
(
Atractor
Caótico)
(6). Considere un campo vectori al autónomo cr (r ;:: 1) en <)\!?
64
(
Ec:. 2)
con f3n = f3" +ó./3n , 1 D./3n 1 t,f3max · Se pueden determinar muchas OPl's del atractor en este
mapa y se puede escoger una de ellas.
Sea F· = P ({F"· /3') el punto fijo inestable seleccionado del mapa P, el cual corresponde a la órbita deseada. Se
pueden observar las itera ciones del mapa cerca de la órbita deseada y obtener las propiedades locales para esta órbita
RO
•
'.
C&nltO
//IV
(f..fex)
VO
i
4, ('Jum 7 5 Agn."l/o} "'ººº
Arríc11 /n

periódica . A fin de realizar esto, es necesario a¡ustar las iteraciones del mapa a una aproxi mación lineal. Esta aproximación en la vecindad de F* y f:J* está dada por
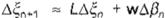
(Ec 3)
donde ti.sn = " - s/, ó.{311 = f3n - [:J* , L = (o I on)P (/ , [:J*), y la derivada parcial de la órbita es w = (o I o{3,.)P (/ . p·). Los valores propios estable As e inestable A.u que satisfacen l l s 1 <1< 1 A.u, 1
pueden ser extraídos a partir del mapa local aproximado. Las variedades estable e inestable denotadas por M5 y M11 • son definidas como aquellas trayectorias que convergen asintótica mente a un punto fijo en tiempo progresivo y regresivo respectivamente,
en otras palabras:
M
5
para t -4 +oo y M11 para t -=. Las direc
ciones de las variedades estable e inestable en el punto fijo están dadas por los vectores pro pios es y eu correspondientes a ),$ y ),11 respecti vamente. Si fs y fu son los vectores
contravariantes definidos por fs·es = fv·ev = 1 y
f
s
eu = f ·es = O, podemos escribir L = /,"euf 1+
11 11
7- sesfsT.
Suponiendo que s., ha estado suficiente
mente cerca de SF tal que la Ec. 3 se cumple, para que la siguiente iteración n- : caiga en la
variedad local estable F*. el parámetro {311 =
f)/3n
+ [:J* , tiene que ser seleccionado de tal
forma que se satisfaga el requerimiento f11 D.n1
= fu·(1H - s/") = O. Tomando el producto interno
de la ecuación (4) con fu se tiene:
t::,P.
== -/.... _f,, ·t.sri

IJn
u
f.
. u
(
Ec
.
4)
donde se supone que f v w 1' O. Es importante mencionar que el resultado obtenido de ll/3n es utilizado para perturbar el parámetro f3 sólo si /Jn
s;
fJmax.• donde 6/3,, > üfJmax· Sin embargo, la per
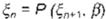 turbación debe ajusta rse a cero. Además,cuan do C,0 •1 cae en la variedad estable F • la pertur
turbación debe ajusta rse a cero. Además,cuan do C,0 •1 cae en la variedad estable F • la pertur
Sin embargo, debido a posibles errores e imprecis10nes en los cálculos anteriores, las iteraciones subsecuentes pueden caer fuera de la variedad
estable. A fin de evitar esto, la nueva ó.f3n tendrá que ser calculada para cada iteración para asegurar que la subsecuente C, n
se aproxime a /.
Podemos dividir los métodos de perturba ciones paramétricas en los siguientes pasos (9):
1. Identificación de Órbitas Periódicas Inesta bles empotradas en el atractor caótico y selección de una de ellas (puntos fijos inesta bles en la
hipersuperficie de sección).
2. Caracterización del desplazamiento debido a pequeños cambios a estímulos externos (introduciendo pequeñas perturbaciones al parámetro accesible del
sistema).
3. Caracterización de la dinámica local del punto fijo.
4. Diseño de la ley de control (cambio correcto en el parámetro tal que el estado sea forzado a caer dentro de la variedad estable de la órbita
periódica).
Movimientos Periódicos Inestables y Puntos
FIJOS
En esta sección se describe la metodologia empleada para encontrar OPl's a partir de series de tiempo .
A diferencia de la técnica OGY, en lugar de utilizar un Mapa de Poincaré como la superficie de sección para encontrar las OPI (7). se utiliza una
herramienta conocida como Mapa de Primer Retorno (MPR). El MPR se obtiene a partir de los máximos locales de una señal caótica y su retrasos en tiempo
para construir un vector de coordenadas retrasadas análogo al utilizado para la reconstrucción del atractor (2). ( 1O).
Para diseñar el controlador sólo necesitarnos una serie de tiempo de cualquier variable del sistema, a fin de formar la serie de tiempo s(n),
y el MPR puede ser expresado como:
bación ó./3
puede ser ajustada a cero. La órbita
para los instantes de tiempo subsecuentes (.;,, . n•J····> debe aproximarse a C,/ en una
razóngeométrica As·
Rev
Centro
'nv
(MelC
)
\/o
l
.
4
Núm
1
5
Agosto 2000
(Ec.
5)
65

donde Pes una función no lineal desconocida y
{J
es el parámetro a perturbar.
Cabe mencionar que el parámetro {J determi na la localización del punto fijo SF dado por:
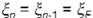
(Ec 6)
Una vez obtenido el MPR, se busca la ubi cación del punto fijo instable que corresponde a
la OPI. Este punto se obtiene encontrando la intersección de la función P del MPR con la línea recta descrita por (Ec. 6).
Caracterización del Desplazamiento ante Pe queños Estímulos Externos
Como se ha mencionado, este método de con trol consiste en producir pequeñas perturba ciones al sistema mediante la variación de pará metro
accesible del mismo. Estas perturba ciones producen un cambio en la ubicación del punto fijo inestable, por esto es importante conocer este cambio.
El valor del parámetro {3 tiene que ser ajusta do en una vecindad del valor del parámetro nominal {J" entre bifurcaciones para
encontrar la
relación entre el parámetro fJ y el cambio en la
ubicación del punto fijo F· Los puntos obtenidos pueden ser aproximados a una línea recta por medio de métodos mínimo cuadrados, y la pen diente m de esta recta es utilizada para crear el vector de desplazamiento g necesario para calcular el vector de ganancia de retroalimenta ción
vector en la fórmula:
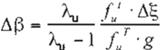
(
Ec.
7
)
donde A.v es el valor propio instable del punto silla y f., es el vector propio de la base con travariante en la linea lización que
se describe en la siguiente sección.
C
a
ra
ctanzacio
n
da la dínam1ca local fmeafizada
El ultimo paso antes de diseñar un controlador tipo OGY consiste en caracterizar la dinámica
66
alrededor del punto fijo inestable. Suponemos que este punto fijo se comporta en forma lineal dentro de una vecindad de este mismo. Para desarrollar
esta identificación utilizarnos tam bién la serie de máximos locales (n) utilizada para crear el MPR.
Entonces, la dinámica linealizada en la vecin dad del punto fijo se puede escribir:
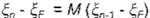
(E
.
8)
donde M es una matriz cuadrada. Debido a que la órbita periódica a estabilizar es instable , el punto fijo correspondiente SF en el
MPR es un
punto silla, luego, este tiene un valor propio inestable y uno estable asociados a él y sus cor respondientes direcciones.
Para lograr el buen funcionamiento del con trol, es necesario que el siguiente máximo caiga sobre la dirección estable. Esto nos lleva a la siguiente
condición:
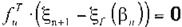
(Ec 9)
Esto significa que el vector de desplazamien to desde el punto fijo al siguiente máximo no tiene componente sobre fu. en otras palabras. cae
sobre la dirección estable (f" es = O). Para esto, es necesario determinar los valores de /,u y de f", es decir
conocer la matriz M.
Utilizando la serie de tiempo s(n) y conocien do el valor del punto fijo es posible determinar la matriz M y entonces se pueden obtener los
valores de A.v y f.,. Esto se logra parametrizando la Ec. 4 con un procedimiento de identificación con mínimos cuadrados.
Esta parametrización consiste en seleccionar una secuencia de puntos de la serie de tiempo
(n)
(al menos cuatro de ellos) en la vecindad del punto fijo inestable . Estos máximos suce sivos deben estar sobre la misma dirección, pero cayendo en
sentidos opuestos alternativa mente.
Rev Centr(· /nv
(M
:} Vol 1
,
Num
15
A9u•(to 20VO
 "-- .--------.- Art ícuIo
"-- .--------.- Art ícuIo

Una vez obtenidos los valores para la matriz M se puede calcular el vector de ganancia de retroalimentación en la fórmula 7.
APLICACIÓN AL CIRCUITO DE CHUA
El Circuito de Chua
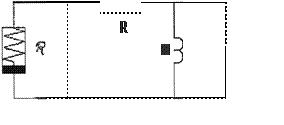
El Circuito de Chua es un oscilador no lineal simple que exhibe una variedad de compor tamiento incluyendo Caos (11}. El circuito con tiene tres
elementos que almacenan energía (un inductor y dos capacitores). una resistencia lineal y una sola resistencia no lineal NR
Las
ecuaciones de estado para el circuito son:
dv
c
J
[ ]
V y G = 560 pS. Para simplificar el diseño, se reformularon las ecuaciones del circuito obteniéndose la siguiente ecuación de estado
equivalente (11):
x
= p [-x + y -/{x)]
y =
x - y +
z
z
= -qy
(Ec
12)
Donde p = C,IC2 > O y q = C/(LG2) > O son los dos parámetros principales que
controlan el comportamiento del circuito y f (vc1) es reformu lada como f (x) representada por:
f(x
)
=
m
0
'
x
+ 1(m/ -m0 'J [lx + Bp J - lx - B,ol]
----ZJ..
=
df
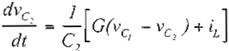 I
I
G(
v
c
- Ve ) -/(ve )
J
1 I
donde m0' = m0 / G > O y m1' = m1!G < O.
(
Ec.
13)
di
¿
J
- = - -v
dt
L
e!
(Ec
.
10)
Para tener resultados consistentes con el cir cuito. los parámetros seleccionados para los parámetros fueron p = 9. q = 14 2/7, m0' = - 517,
m/ = - 817. Para estos valores se puede obser
var un atractor extraño conocido como la Doble
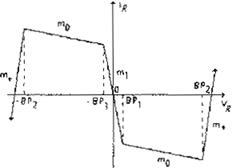
donde G = 1/R y f(vc 1) es una función seccional
mente continua definida por:
/(ve,)
=
movc,
+
1
(m,
- mo )
[lvc, + Bpl -lvc, - Bp l]
(Ec
.
1
1)
La resistencia no lineal, también conocida como Diodo de Chua. puede ser construida con componentes fáciles de conseguir, y posee una curva
característica de voltaje vs. corriente (v-í) de tres segmentos. Las pendientes en las regiones interior y exterior son m 0 y m1 respecti vamente . ±Bp denota los puntos de ruptura.
Espiral.

 t
t
Figwa 1
{a
)
Circuito de Chua
Este sistema despliega comportamiento caótico para C1 =56 nF, C2 = 5.6 nF, L = 1O mH,
m
0
= - 757.5757 µS, m 1 = - 409.0909 µ.S, Bp = 1
Rev. Cenrro
/11v.
(Mex)
Vol 4
.
Nüm
.
15 Agosto 2000
 F
ígura
1
(D
J
característica de
V·i de
F
ígura
1
(D
J
característica de
V·i de
ta
res1stenc1a
67
Se seleccionó G como el parámetro a pertur bar. y la variable medida fue z.
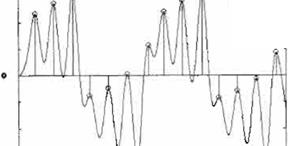
Movimiento periódico inestable y puntos fi1os
El parámetro nominal {J* = f3 = G fue 14 217. Numéricamente, se obtiene el punto de inter sección calculando el centroide
de masa de los puntos de P en la vecindad del punto fijo. Las
coordenadas de la intersección proveen la ubi cación del punto fijo buscado (SF· l;,F) = (2.9652,
2.9652).
. · - -1
 1
1
tro y la ubicación del punto fijo SF· Esto se reali zó para el intervalo ,B [13.1, 15.5).
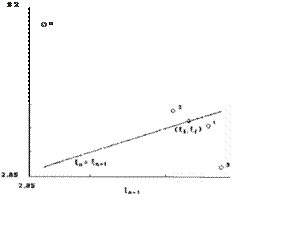
En la figura 3 se pueden observar los puntos obtenidos para cada valor del parámetro {3. Estos puntos fueron aproximados a
una recta de forma y = mx + b utilizando un algoritmo estándar de identificación por mínimos cuadra
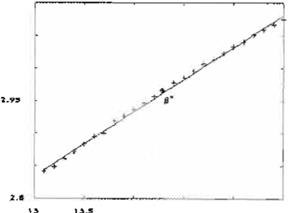
dos;se obtuvieron los valores m = 0.0988 y b =
1.5496. Luego, el vector g es g =
[0.0988,0.0988)T .
 -·
-·
t,
o 10
-1-5 lo
B
3
Puntos
flJOS
instebles ;F
vs.
 Fi
gura
2 (a) Serte de tiempo para obtener ef MPR
Fi
gura
2 (a) Serte de tiempo para obtener ef MPR
 !1.5
!1.5
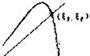
\ \
o .
f . \ '\\
1
·• . /------- ----'----'
•l o
F
igura
2
(b
)
MPR
y
fa linea
n
= n-1 ulilizados para obtener el punto fijo ( F· F)
Caractenzac1on del desplazamiento del punto fijo ante estimulas externos.
El valor del parámetro f3 fue variado entre bifur caciones alrededor del valor nominal {J* a fin de encontrar la relación entre el
valor del paráme-
68
Figura
valores del parámetro
L3
y
Ja linea
rect6
a
proximada
utilizando mínimos cuadrados
.
Identificación de la dinam1ca local
La parametrización consiste en seleccionar una secuencia de puntos de la serie de tiempo s(n) (al menos 4 puntos) en la vecindad del punto fijo. Estos
maximos sucesivos deben caer en la misma dirección, pero en sentidos opuestos en
 forma alternativa, esto se aprecia en la fi,gura 1·
forma alternativa, esto se aprecia en la fi,gura 1·
Figura
4 Puntos consecuiívos dei MPR utilizados parCJ .Jblener la matnz M
Rw
Cenlro l:?V (Me.<) Vol
..;, Num 15 Agosto 2000
Artículo

 Utilizando un procedimiento de identificación por mínimos cuadrados, obtenemos el valor de M , calculamos sus valores y
vectores propios y los vectores propios de la base contravariante:
Utilizando un procedimiento de identificación por mínimos cuadrados, obtenemos el valor de M , calculamos sus valores y
vectores propios y los vectores propios de la base contravariante:
-
¡-0.0162
0.9950
l
M
- 1.8894 - J.6874
A = [ 0.7539]
-2.4575
y,
[0
.
9613]
fu =
0.3918
X
_,
-2.5
l.
Figura 5
(b) OPI
controlada
Con estos valores es posible calcular el vec tor de ganancia de retroalimentación de la fórmu la OGY.
Resultados Numencos
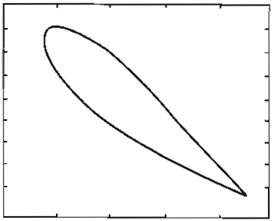
Este método fue aplicado utilizando perturba ciones paramétricas calculadas con la Ec. 5 para controlar una OPI empotrada en elatractor de Doble
Espiral de Chua. En la figura 5 (b) se muestra el sistema controlado.
El método de OGY es probablemente el más popular para controlar sistemas caóticos debido a la posibilidad de implantarlo sin la necesidad de conocer la
dinámica explícita del sistema, es suficiente con utilizar una serie de tiempo de mediciones experimentales. Esto no significa que sea una tarea
sencilla. está compuesta de dos etapas principales: una que se desarrolla fuera de línea (el diseño del control propia mente) y la aplicación del
controlador a la plan ta.

o
... o
........ _ __
..
Se puede utilizar cualquier variable medible del sistema y cualquier parámetro accesible para aplicar las perturbaciones al sistema. Para
implantaciones experimentales del control. el ruido y los errores inevitables de procesamiento de señales puede causar que el controlador no
funcione de modo tan efectivo como en ausen cia de éstos. En otras palabras. antes de establecerse en la respuesta deseada. el sis tema puede tener
transitorios caóticos cuyas longitudes pueden variar de acuerdo al momen to en el que el controlador sea encendido.
Figura
5
(a)
Atractor
CJe Doble
Esplfaf
de Chua
.
El método OGY original {1) sugiere la uti lización del Mapa de Poincaré, este mapa se puede formar haciendo un corte transversal del atractor en el
espacio de estado. Este mapa contiene la dinámica del sistema en una dimen sión menor. El problema es ubicar dónde hacer el corte para encontrar el
mapa de Poincaré más adecuado; es decir. el mapa que ofrece
mejores ventajas para encontrar el punto de equilibrio y para caracterizar la dinámica. La uti lización del Mapa de Primer Retorno ofrece ven tajas significativas a este respecto pues permite una
mejor identificación de la dinámica del sis tema.
El control de sistemas caóticos es uno de los campos de investigación más promisorios den tro del estudio de sistemas dinámica no lineales y representa un
gran reto en muchos campos. A partir de su desarrollo puede verse que en el futuro no solamente nos dará resultados satis
factorios a problemas actuales sino que nos
proveerá de muchas ideas nuevas.
REFERENCIAS
(1) Ott, E., C. Gregbogi, & J. A . Yorke, Conlrol ling chaos, Phys. Rev. Lett. 64, p.
1196, 1990.
(2) Abarbanel, H. D. l., Analysis of observed chaotíc data, Springer-Verlag, 1996.
(3) Chen, G. & X. Dong, From chaos to order: methodologies, perspectives and applíca tions, World Scientific, 1998.
(4) Grassberger, P. & 1. Procaccia, Characteri zation of strang e attractors, Phys. Rev. Lett. 50, pp. 346-349, 1993.
(5) Nitsche, G. & U. Dressler, Controlling chaotic dynamical systems using time delay coordinates, Physica O. 58 p. 153, 1992.
(6) Wiggins, S., lntroduction to applíed nonlinear dynamícal systems and chaos,
Springer Verlag, 1990.
(7) Auerbach , O , C. Grebog1, E. Ott, & J. A. Yorke, Controlling chaos in higher dimen sions, Phys. Rev. Lett. 69, p.
3479, 1992.
(8) Nayfeh,A. & 8. Balachandran, Applied non linear dynamics· Analytical. computational and expe rimental methods, Wiley & Sons, N. Y , 1995.
(9) Oitto, W. L., S. N. Rausseo & M. L. Spano,
Experimental control of chaos, Phys. Rev.
Lelt
6 pp. 3211-3214, 1990.
(1O) Álvarez-Gallegos, J. & H. G. Gonzalez-Hemán dez, Analysis of the dynamics of an under actuated robot: the forced Pendubot, Pro ceedíngs of the IEEE 36th lntematíonaf Conference on Decision and Control COC'97, San Diego, CA . pp. 10-12, di ciembre, 1997.
(11) Matsumoto, T., L. O. Chua & M. Komuro,
The double scroll, IEEE Transactíons on Circuíts and Systems, vol. 32, pp. 798-817, 1985.
![]() casos, la estab1hzación de órbitas periódicas inestables. Esto nos lleva a diferentes enfoques de control (3) como los métodos de control de
"rediseño". métodos de perturbaciones para métncas, métodos de fuerza externa y métodos de ingeniería de control.
casos, la estab1hzación de órbitas periódicas inestables. Esto nos lleva a diferentes enfoques de control (3) como los métodos de control de
"rediseño". métodos de perturbaciones para métncas, métodos de fuerza externa y métodos de ingeniería de control.
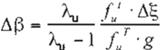
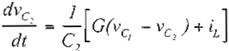 I
I
 t
t
 F
ígura
1
(D
J
característica de
V·i de
F
ígura
1
(D
J
característica de
V·i de
 1
1
 -·
-·
 !1.5
!1.5
 forma alternativa, esto se aprecia en la fi,gura 1·
forma alternativa, esto se aprecia en la fi,gura 1·

 Utilizando un procedimiento de identificación por mínimos cuadrados, obtenemos el valor de M , calculamos sus valores y
vectores propios y los vectores propios de la base contravariante:
Utilizando un procedimiento de identificación por mínimos cuadrados, obtenemos el valor de M , calculamos sus valores y
vectores propios y los vectores propios de la base contravariante:
