Quantum Chemistry and
Its Application to
Life
Science
Universidad
Iberoamericana-Golfo
Centro
Km.
3 5 Carr. Fed Puebla-Atlixco
A
P.
1436
C P 72430
Puebla, Pue.
Mex1co
<nonovera@wagc.pue.
wa.mx
>
RESUMEN
Para lograr penetrar a la esencia de las reacciones químicas y de los fenómenos biológicos, uno tiene que apoyarse inevitablemente en la teoría
cuántica que describe interacciones entre átomos y moléculas. Sin embargo, es generalmente 1mpos1ble analizar o diseñar analíticamente las estructuras
de moléculas exactamente sobre la base de la mecánica cuántica, a excepción de algunos casos especiales. Así se ha
desarrollado una variedad de métodos de aproximación en química cuántica, contribuyendo enorme mente al desarrollo de la química y sus campos de
aplicación. En este trabajo describimos los conceptos importantes de la quimica cuántica, tales como el método orbital molecular. la teoría de la
frontera del electrón, la interacción intermolecualr, etc. y revisamos sus aplicaciones en los campos de la vida científica. Palabras clave: teoría cuántica, método orbital molecular, teoría de la frontera del electrón. interacción molecular.
ABSTRACT
In order to get insight into the essence of chemical reactions and biological phenomena, one inevitably has to rely upon the quantum lheory which
describes interactions among atoms and molecules. However, it is generally impossible to analyze or design analytically the structures of molecules
exactly on the basis of quantum mechanics excepl sorne special cases. Therefore a variety of approximate methods have been developed in quantum
chemistry, thus greatly contributing to the development of chemistry and íts application fields. In this paper we describe the important concepts in
quantum chemistry such as the molecular orbital method. the frontier electron theory. the intermolecular interaction, etc. and review their
applications to the lite science fields.
Keywords. quantum theory, molecular orbital method. trontíer electron theory, intermolecular interaction.
INTRODUCTIOi\I cognized that quantum mechanics forms a basis of not only physics but also chernistry.
Quantum mechanics was established in 1926
when E. Schródmger formulated the wave equa tion, the Schrodinger equation, and indepen dently to him when W. Heisenberg formulated the malrics
mechanics. Nowadays it is well re-
The question how atoms are combined to form a molecule has been a long-time puzzle. In 1916 G.N. Lewis presented an idea supportin9
that when forming a molecule out of neutral
atoms. two of these atoms share a pair of elec trons to create a combining force . However, the reason why a combining force 1s generated in
such a way was not clear. In 1927, one year
after the foundation of quantum mechanics. W. Heitler and F. London clarif1ed the issue of what force acted arnong two neutral hydrogen atoms to form a
hydrogen molecule by solving the Schrodinger equation. The concept of "covalent bond" which is so common nowadays derives from the wave behaviour of
electrons. Such con
cept could not have been understood without quantum mechanics.
The d1scovery of the periodic table of ele ments dates back to 1869 when D l. Mendeleev found that the chemical nature vanes penod1cal ly when
chemical elements are arranged in the arder of atomic weight At the time of d1scovery of the periodic table, which was created deduc
tively from the chemlcal nature of elements. it was cons1dered to be a pure empírica! rule. However. as the construction of quantum mechan.es
progressed and the atomic struc tures were more clearly understood, 1t became clear that the period1c table originales from the quantrniTl-mechanical
concept of "ort)ital". The present penodic table describes how many elec
lrons are localed in each possible atomic orbital. The elements which oelong to the same group in the periodic table possess a similar configura tion
for the "valence electrons" wh1ch occupy the ou1ermost orbital. The valence electrons play crucial role in determining chemical nature of atoms. In lus
way the period1c table can be understood fro1r· the standpoint of electron con figuration in atoms built according to the quan tum-mechanical
principies. This fact already
indicates cfearly that the bas1c principies in chemistry are based on quantum mechanics.
As pointed out by P.A .M. Dírae ( 1), ali of the issues in chemistry can be clanfied by quantum mechélrncs in principie. However, it is generally
imposs1ble to analyze or des1gn analytically the structures of molecules strictly on the basis of
quantum rnechanics except a few speclal cases. Therefore a variety of approximate methods have been developed in quantum chemistry
(2-5), thus greally contnbuting to tt1e developrnent of

concept of the molecular orbital method one can calculate and understand a variety of properties of molecules as well as the mechanism of their
chemfcal reactions.
Ouantum chernistry is also deeply related to the life science fields such as pharrnacology and medical science. Th1s is because lhe mecha nism of
various reactions in an organism can be understood by quantum chem1stry. Quanturn chernistry plays also a crucial role ln under standlng deeper the
essence of "life" by clarify
ing various properties of biopolymers (proteins. nucleic acids. etc.).
In Section 2 we explain the molecular orbital method wh1ch forms a basis of quantum chem- 1stry, and in Section 3 and Section 4 we describe the
frontier electron theory and the intermolecu lar interaction !ogether with its appllcations to life science fields, respectively. Section 5 sum
rnarizes the paper
Molecular 01bital Method
The Schrodinger equation which describes the electron behaviour mov1ng around a nucleus 1s expressed as follows:

( E 1
1)
Where f1 , the Hamilton1an operator of the
electrons. consists of two terms: the kinelic energy of electrons moving around in the fiefd of
a nucleus, ye and the Coulomb potentíal ener gy between electrons and nucleus. V. That is,
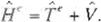
(Eq
.
2)
The symbol " in H"' tor example, expresses
that H" , is the operator and the subscript e means that it describes electron(s). Uslng the
• and V are expressed
trons in an atom or molecule can be described
by means of atomic orbital functions ar molecu lar orbital functions, respectively. By using the
52
as
Rev Cemro
lnv
.
/MexJ Vor
.
t.
Num
15
A
go
sco
::.
o
ca
Artículo

..... d< t ln11Jt mtc ft 1 z rl<'ttro,l\ J
V =
-
L ¿ ¿_ + L-. '
u " TLL4 l•»' I !'"
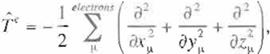 (Eq 3)
(Eq 3)
expressed by lhe so-called Slater matrix which islhe combmation of molecular orbitals to which each eleclron belongs. In the case when an
electron with spm a and an electron with spin.
1 are located m one molecular orbital <i>, and correspondingly 2n electrons are located tn n
molecular orbitals, the wave function, 'W '"·can be expressed as
(Eq 4
)
respectively. !n the atomic unlt systern one uses as the fundamental units the rnass of electron,
41,rl)o\ 1) <j>1\l iI C) <I> tl (.( ( 1) ... '1'.tl\Ll:i

 1 •P1l2lf1{2J 4.,r'.!)llt'i -t';<:d 2J <i.t2)(\! \
1 •P1l2lf1{2J 4.,r'.!)llt'i -t';<:d 2J <i.t2)(\! \
'I' JM
m, tl1e Planck consta11t devided by 2rt ,f/(= h / 2rr.) and e:! / 4m.;,, (e; the absolute value of electron charge). In this systern
the unit or length is measured by ñ2 / m/ and the unit
of energy is measured by me• / t/ . ZA is the
charge of the nucleus of an atom A. Since the kinetic energy of electrons and the electrostatic
potential energy between the µ- th electron and the nucleus A depend only on the coordi nate of the µ- th electron, they are called
one electron term. On the other hand, the Coulomb repuls1on energy between the µ- th and i·- th electrons depends on the
coordi nates of two electrons, hence is called two-elec
tron term. Separating the Hamiltonian of elec
trons into the one-electron term and the two etectron term. one can wlite:
lf'1 (•) .( 2.11) q112Jl¡í2nl t21 1'(t( /1) .. .. 11n1¡\1l1rJ
(Eq.
7)
where /J(2n)i. is a norrnalization constani. Assummg that the molecular orb1tals constitute the normallzed orthogonal system, one can write
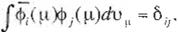
(Eq.
8)
where i is the complex con1ugate of <Pi and
O;j
is Kronecker's synibol taking the value 1 for i
::: j and O for i:t. j. The total energy of electrons 1s
T
-f
="¿HA ( t ) + "-_I ,
obtained
by multiplying the complex conjugate
A
where H( t) is
!l.
µ> ...,\'l.J
(Eq 5
)
of tlJ (' to each side of (Eq. 1) from the left and
1ntegrating 11 over the whole space. That 1s.
E
=
¡
·
·H\v '.du,
=
2 H, +
¿:(2
.f,1 -
K; ).
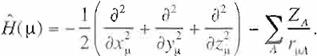 1 l ,J
1 l ,J
The wave function of electrons, \V •, is
rEq 6)
where H¡. J¡j and K¡j in (9) read
(Eq 9)
Re''
ren m lrw (Mex) Vol Ntím. 15 Agosto 2000 53
 Ar1íc11lo
. - -
Ar1íc11lo
. - -

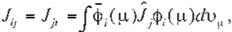 H
,
=J .H(µ)t>,(µ)du ,,
H
,
=J .H(µ)t>,(µ)du ,,
(
Eq.
1
0)
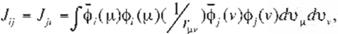
(
E
q
.
11
)
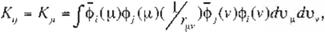
(
E
q
1
2)
respectively. H¡, which is called "core integral", is the energy of an electron in a molecular orbital. <!>,, moving in the attractive fíeld of
elec
trostatic potentlal of !he nucleus. Jij• which is
called "Coulomb integral", is the repulsion ener gy between an electron in a molecular orbital,
<l>r and an electron in a molecular orbital, J.,
I
K¡j, which is called "exchange integral". is speci- fic to quantum mechanics and is derived from
the fact that the wave function is expressed by
the Slater matrix, (Eq. 7). Note that differing from Hi and Jíj• K¡j cannot be 1nterpreted by the
classical term. Furthermore defíning the Coulomb operator, }; ,and the exchange opera-
tor, K,, as
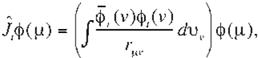
(Eq. 13)
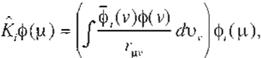
(Eq 14
)
J¡j and Kij in (Eq. 11) and (Eq. 12} can be refor mulated as
(Eq 15)
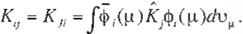
(l=
Q
16
1
The molecular orbital óE can be obtained from
\he condition that lhe totalenergy of electrons , E, in { Eq. 9), takes the minimurn value for the real molecular orbital. To fulfill
such condition ,
the variation óE has to equal to O when et>, gets small changes. <i>;----;.<!>; + 6cp,. in (Eq. 9).
Thuslaking the variation of (9), we obtain
o
E =
¿oH, + :¿c20111 - oK,,).
¡
i
,j
(
E
q
17)
where
oH;, ol, andóK;; in(17) read
ófJ
,
Jo$,(µ)J (µ)<!>,(µ)dt•,, +J$,(µ)H(µ)o<P,( µ)du,, .
(
E
q
18)
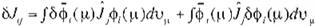
(Eq 19
)
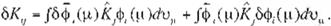
(
Eq.
20
1
One has to derive the equations under the
normalized orthogonal conditíon for $;. i.e. (Eq. 8). Thus taking the vanation of the normalized orthogonal conditíon in (Eq. 8) as:
 54
Rev Centro
lnv (M-,x)
V
ol
4
N'Jm
15 Ago ro 2000
54
Rev Centro
lnv (M-,x)
V
ol
4
N'Jm
15 Ago ro 2000
Art [cu lo

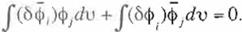
(
Eq
2 1
)
Summing up (Eq 21) multiplied by an unde tennined constant, -e,,and the (Eq. 17), we
obtain
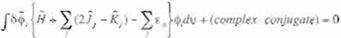
(Eq
22)
In order to hold {Eq. 22) for arbitrary o<j>1, the follow ing conditions should be satisfied.
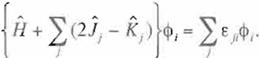
(Eq 23)
The elements of Hermítian matnx € ;1 can be diagonaliz.ed by a unitary transformation. Denot ing the diagonalízed value of e ,1 as e, and introducing the notatíons:
tion directly by numerical integraUon is almost impossible except for simple diatornic molecule cases. Then to proceed further,we assume that t he wave
function of an electron in a
molecule. <P; (molecular orbital). is expressed
by the combinatton of the wave functions X r
(atomic orbital) of electrons in atoms which con stitute the molecule as:
et>, = 2x,c,,..
r
(Eq.
26
)
Since in (Eq. 26) the molecular orbital (MO) is approxirnated by the linear cornbination (LC) of atomic orbitals (AO), such approxirnation 1s called
LCAO-MO method. Substituting (Eq. 26)
into (Eq. 25), multiplying it by <P,' frorn the left
and integrating it over the whole space. one can get the following Hartree-Fock-Roothaan equa tion:
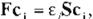
(Eq.
2
7)
F
=
i-1+
¿c2J
)
- K),
(Eq
24
)
where c1 and S are matrices. The Fock opera
tor, F is expressed by the sum of one-electron '
term, j.¡ , and of two-electron term, pA ' as
(Eq. 23) can be expressed as:
A A
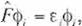 F =
H +
P.
F =
H +
P.
(E
q 25
)
(Eq. 25) is called Hartree-Fock equation.
In case of an atom, !he Hartree-Fock equation becomes one dimensional íntegro-differential equation with a variable r, a distance from a
nucleus to an electron.and thus it can be solved numerically with high accuracy. In case of a mol ecule, however, solving the Hartree-Fock equa-
R
v Centro lnv (Mex) Vol 4 Núm 15 Agosto
2000
(Eq. 28)
Putting the Fock operator F, between x,(µ)
and x,( t ) and integrating it over the whole space (v ,) of the µ-
th electron, one gets
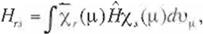
(
Eq.
29)
5
5
 Artículn
Artículn
P,
,
=J x üt>Px ,(µ)d'-\.. = ¿Prs.111 • D,,,,
'·"
(
Eq 30)
where
D
"' =
_¿ 2,-.·.,.,c ..
j
(
E
q.
3
1
)
l
secular equations and obtaining a set of C¡,.,
one can compose the molecular orbital from (Eq. 26). However, one can realize from (Eq. 31) that the system of (35) 1s not salvable without
knowing the LCAO coefficient,
l ,, . So usually one proceeds as follows: first solve (Eq. 35) and
obtain by assuming in sorne way values of
r
e
,,
.
Next. use thus obtained F,.J and solve agam the system of (Eq. 35) to gela new set of e,,. lf the new set and the old set of c,r .do not coin cide, the systern of (Eq 35) should be solved by
using F, with the new set of e". This proce-
and
P,.-'·"'
= (rs 1 tu) - 2 ( rt 1 su),
(Eq.
:
I
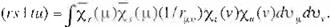 (Eq
.
3
3
)
(Eq
.
3
3
)
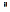
dure is repeated until the two seis of C¡, con
verge to coincide. The converging solutions obtained in this way are sa1d to be self-consís tent(SC) and correspondingly the molecular orbitals are
saíd to be in a self-consistent-field (SCF). This method of deriving the molecular orbitals 1s called LCAO-SCF-MO method. Until now, we have derived
the equat1ons assuming the closed shell system. In the case of the open shell system one can proceed similarly.
The elements of matrix S are expressed as
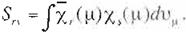
(Eq.
34)
Now mult1plying Q),. to both sides of (Eq. 25) from the left and integrating over the whole space of the ·- th electron, one
gets
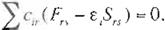
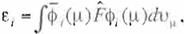 Rewnt1ng (Eq. 27) as
Rewnt1ng (Eq. 27) as
= H1
+ L (2./11
J
- K,1 ).
where
(
Eq
. 35)
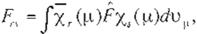
(
Eq.
36)
(F.q
37
)
The first term in the ríght hand of (Eq. 37) rep resents lhe sum of lhe kinetlc energy and the Coulomb energy (in the field oflhe nucleus) of
the electron in the molecular orbital, <!>,, and the
second term represents the repulsion energy among the electrons. The energy which inclu
we obtain the secular equat1ons representing a systern of linear equations of C;,. So 1v ing t he
5
6
des all the types of electron energy in the mole- cular orbital, <1>,. 1s called orbital energy.
Rev Cnlro /11v.
(Mex)
Vol
.: N11m 15 Agosto 2000
Artículo

The orbital energy e; is related to the ionization energy and/or electron affinity.
In the case when 2n electrons enter into n
molecular orbitals, <P;(i = l - n), one can lrans
form the equations by assigning these 2n elec trons to each atom or each pair of atoms as fol lows:
2n = 'l:J2 ¡(L)4>,(µ)du,,
1
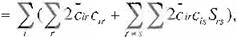
= l:J2¿x,ü•)c..._¿ x.(µ)clSdu,\ '
= }: [¿{2: (2¿"e;, +
2 i,:(Ú
;,e,,S,, >}].
' \ r(Etl) R(,.,1)s(€B)
= 4{, )(D,, + 111> ' 'D,_, , S,)},
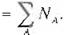
(Eq. 38)
In rewriting the formulas we used the normali
zation condition for each AO. 1 1 means the summat1on over the atomíc orb1tals r belongíng to an atom A. The density matrix D,s is defined
by (Eq, 31) and the overlap integral S,.s is
defined by (Eq. 34). NA 1s a number of etectrons belonging to the atom A.
The molecular orbital (hereafter abbrev1ated as MO) method (2) can be classified into three types. In lhe arder of accuracy of approximation from the
lower leve! to the hígher level they are:
!he empirical MO method, !he semiempirical MO method and the ab m1tio MO method
• Empirical 1\110 method
Simple Hückel method, Extended Huckel method.
Rev
Cen!ro
/nv
(Méx)
Vol
4,
Núm 15 A
g
osto 200
ú
• Semiemplrical MO method
PPP(Pariser-Parr - Pople) melhod, CNDO (Complete Neglect of Diíferential Overl.sp) method, INDO(lntermediate Neglect of Oif ferential Overlap) method,
MINDO(Modified INDO) method, MNDO(Modified Ncglect of Diatomic Overlap) method. AM1 (Aust1n Model 1) method, MNDO-PM3(Pararnetri c Method 3) method,
etc.
• Ab initio MO method
The Huckel method employs the appoxima t1on where there 1s no interactioN arnong elec trons, so that the entire Hamiltonian is repre sented by a sum
of only one-electron Hamilton1- ans. In the case of the simple Hückel method which taKes into account only the contributlons of p electrons the secutar
equahon takes a rather simple form. In the early stage of devel opment of the MO method, thrs method was applied mamly to larger molecules such as
aro malic hydrocarbons to predicl the behaviour of carbon atoms which are sensitive to elec trophilic substitution reactions and/or nucle ophilic
displacement reactions. The method was also applied to saturated hydrocarbons treating s eleclrons. The extended Huckel method does not d1stmguish !he
s eledrons from the p elec trons and 1n add1t1on 1t takes into account the contributions of all valence electrons. Even now, this method is sometimes
applied to the calcula tions for a large system including transition met als. In lhe enipirical MO methods one seldom calculates the integrals which
appear on denv- 1ng the secular equat1on lnstead of calculat1ng
lhe integral values, one rather treats them as parameters whereby drast1cally símpl1ty1ng the secular equat1on and shortening t1e calculat1on time.
However, the results obtained remain solely at qualitative leve!
In the semiemp1rical MO methods one uses sorne sort of approximat1ons to s1mplify cafcula tion of the Fock operators. There are a vanety of
approximations wh1ch allow more quantitat1ve considerations than in the case of the empirical methods. lt may safely be accepted that lhe cal culated
heats of formation using the MNOO PM3 method reproduce well the experimental values However, when using the semiempirical MO methods, one has to be
careful what approximations were used and which experi mental values were used far the integrals.
57

The ab initio MO method does not rely upon any approximatíons in calculating the Fock oper· ators. However, the method is not almighty The accuracy of
!he ab initio MO method depends on lhe quality of the basis functions and the type of wave functions applied. There are a variety of bas1s functions
which can be selected depending on the purpose of the calcu lations. Correspondingly one has to decide what level of basis functions or wave functions
should be used depending on what physical quantities are to be calculated. Thanks to the recent rapid advance in computer technology the ab initio MO
method is now finding wide applications.
 The structures of molecules obtained by the ab initio MO method have been compared so rar with the ones obtained by experiments in vari· ous cases and
the level of reliability of the struc tures by this method (depending on the basis functions used) is now well established. Now the structures
obtained by the ab initio MO method are seldom questioned if only one is careful in choosing the basis function system. Moreover, not only the mosl
slable structure for a molecule. bul also olher structures and their relative stabilities can be analyzed by calcula tion. Although the most stable
structure can be achieved by experiments as well, it is difficult to realize unstable structures experimentally. Therefore , the ab initio MO method
can provide with the precious informations on the molecular structures of various isomers and the 1rrelative stabilities and/or the molecular
structures in the excited states.
The structures of molecules obtained by the ab initio MO method have been compared so rar with the ones obtained by experiments in vari· ous cases and
the level of reliability of the struc tures by this method (depending on the basis functions used) is now well established. Now the structures
obtained by the ab initio MO method are seldom questioned if only one is careful in choosing the basis function system. Moreover, not only the mosl
slable structure for a molecule. bul also olher structures and their relative stabilities can be analyzed by calcula tion. Although the most stable
structure can be achieved by experiments as well, it is difficult to realize unstable structures experimentally. Therefore , the ab initio MO method
can provide with the precious informations on the molecular structures of various isomers and the 1rrelative stabilities and/or the molecular
structures in the excited states.

unoccupíed molecular
orbital
occupied molecular orbital
Frontier Electron Theory
K. Fukui of Kyoto University was awarded a Nobel príze for chemistry in 1981 by his achieve ment in lhe "frontier electron theory"(6). According to
the theory, it is poss1ble to predicl in which part of a molecule and w1th what proba bility a certain chemical reaction can take place by examining
the orbital energy of the specific orbital called "frontier orbital". signs as well as size of the LCAO coefficients. The MO method allows to know the
location in the molecules where and wilh what probability a reaction takes place. When 2n electrons are located on n molecular orbítals. these n
orbitals are called occupied orbitals. On the other hand the orbitals in hígher energy where no electrons are located are called unoccupied orbitals
Among the occu pied orbitals the highest occup1ed molecular orbital HOMO is most related to the reactions. Among the unoccupied orbitals the lowest
unoc cupied orbital LUMO is most involved in tl1e reactions. The HOMO and the LUMO are both called fronlíer orb1tals, and the electrons which occupy
those orbitals are called frontier elec trons (Fig. 1).
The frontier electron theory predicts the loca lions in a molecule where reactions take place wíth the highest probability as follows:
• An electrophilíc reaction takes place al the location where the (probability) density of elec trons belonging to the HOMO 1s !he h1ghest. that
is. the place where 2 (cHOMO,r)2 takes the largest value.
LUMO (Lowest UJ\occupied Molecular Orbital)
<E" HOMO (f-J1ghest Occupied Molecular Orbital)
Q :an dectron occupying each molecular orbi tal
Fígure 1.
,A nucleophilic reaction takes place at the Jocation where two electrons are located on the LUMO. that is, the place where the density of these two e/ectrons. 2(cLUMO.r)2, tekes the largest v alue.
• A radical reaction takes place al the location wl1ere the sum of density of two electrons, one on the HOMO and the other on the l UMO takes the largest value
58
Rev. Ce
n
tro
l
nv
(
M
1
'x) Vol
4. Num. 15 Agosto 2000
 L .- A ni<:ulo
L .- A ni<:ulo
Befare the invention of the frontier electron theory (1952), the necessity had been believed to examine in detail all the orbitals where elec trons
are located in order to find the location where react1ons go with high probability. Fukui could s1mplify the situation by showing that it is enough lo
examine only the HOMO in the case oí electrophilic reactions while the LUMO in the case of nucleophilic reactions among those orbitals.
This method was established in 1952 by applying the Hückel method to aromatic hydro carbons (conjugated cornpound) and compar ing the results with a
number of experimental facts . lt has been demonstrated that the maxi rnum factor deciding reactions is the stabíliza tion due to the localization of
electrons in the transition state. That is. 11 is the frontier elec trons lhat contribute at most. Thanks to such progress of the theory and computer
(7). nowa days, it has become possible to realize in com puter graphics simulation film on the basis of
the accurate calculat1on by the ab initío MO melhod, far example, how, when a reagent atlacks a molecule, both molecules produce products.
INTERMOLECULAR INTERACTIONS
In molecular assemblies,lhere arise interac lions among molecules. As in the case with covalent bonds which combine two atoms to form a molecule, the
origin or the intermolecular inleraction between two molecules is also a quantum-mecharncal force. When the molecu lar interaction becomes stronger,
chemical react1ons take place by accompanying discon neclion or formation of covalent bonds. There are always ín1eractions albeil not so strong
between molecules.
lntermolecufar lnteractions m a Living Body
In a living body we encounter a si1uation in which molecules are distributed not at random. but rather specific intermolecular interactíons are
functiornng so \hal specific molecules are combined with certain inevitability or regularity. In addition, as in !he case with antigen-antibody
react1on, molecules specifically recognize another molecules, whereby identifyíng and eliminating objects which m1ght be danger to the normal existence
of a living body, or. on the
Rev. Centro lnv (Méx) Ve! 4
,
Num 15 Agosto 2000
contrary. collecting or accept 1ng objects which
are
necessary for \he living body.
When certain molecules maíntain physiologi cal activity in a living body, there exisl the inter actions between these molecules and the biopolymers
that accept them. lf the molecules from another site manage to specifically couple with biopolymers such as prolein, we say that
the molecules have been "recognized". These molecules are called a ligand (substrate) and a receptor, respectively. Oiscovering a ligand with
higher binding activity can lead to developrnent of effective medicaments .
In order to 1dentify a ligand with higher bind ing activity, one haslo identify a molecule which possesses stronger interaction. In general in order
to synthesize various molecules by repeating experiments in laboratory one needs enormous time and money. On the other hand the quantum chemical
technique allows one to calculate the molecular interaction energy and
charge distribulion, and so on, with reliable pre cision. The eleclrostatic force which is a far reaching force plays an important role when a
biopolymer such as protein and nucleic acid interacts with a substrate. Thus, the knowledge of !he charge distribution on the molecular sur face
prov1des the information about a global nature oflhe molecular interactions.
The situation where a molecule A "recog nizes" a molecule B, but it does not "recognize" a molecule C is controlled as follows: When the A
"recognizes" !he B.lhere exists specific inter molecular interaction between these molecules. In other words the "recognition" between mole cules
occurs only when such specific interaction exists and if there is no such molecular interac tíon belween the molecules A and C, the mole cule A does
not "recognize• the molecule C.
Hycirogen Bond
lt is a hydrogen bond that plays the most crucial role in the recognition between molecules. The hydrogen bond is generally represented as -X HºY-.
where X is an atom wilh large electroneg ativity such as N (nitrogen atom) and O (oxygen atom), so that a X-H bond has strong polarity: electrons are
attracted to X and H (hydrogen
atom) is slightly positively charged (o+). An atom Y possesses large elec tronega tivity and is
59
 Ar1íc11 /i1
-
Ar1íc11 /i1
-

slightly negat1vely charge Wl. Thus the hydro gen bond is generated by the interaction between X-H w1th strong polarity and Y with large
electronegativity. The main feature of the hydrogen bond consists in its directional1ty. When X-H lines up with Y, the interaction energy becomes most
stable A concrete image of the interaction between the pept1de main chains comprising protein is as shown in Fig. 2. Thus when N-H hnes up with O=C, the interaction between pept1des becomes most stable. On the other hand 1f the angle between N-H and O=C is
dev1ated far from 180º. no stable hydrogen
bonds can be formed between peptides.
In this way the stable hydrogen bonds are formed only when certain spec1fíc atoms exist in a specif1c configuration. They play the leading role a
specific molecular interaction. An ant1gen antibody reaction is often compared to a rela tionship between a key and keyhole.
In the antigen-antibody reaction it is the hydrogen bonds that play the leading role of specific recognition reaction

lC-0 H - N
)
""'ca a
There are 8 types of hydrophobic amino acid, 4 types of charged amino ac1d and 8 types of polar amino ac1d among the amino acids that form normal
prote1n.(8) lt is the cl :arged amino ac1d and the polar amino acid that are maínly mvolved in the formation of hydrogen bonds. The 1nteraction between
the charged groups is sometimes called an ionic bond. However, actu ally, the interaction between the charged groups includes largely characteristics
of hydrogen bonds. Far exarnple, the interaction between a
negatively charged carboxyl group ( -coo- )
and a positively charged amino group (- NH; )
is duelo a hydrogen bond whose slabihatlon energy shows strong d1rect1onallty.
The hydrogen bond energy is about a few kcal/mol and such hydrogen bond 1s not stably formed unless both molecules are close enough. The
distance-dependency and angle dependency of
Applications of Ouanturn Chernistry to Life Science rields
1able hóm.:n bond 'tble hydro.i:r\ boncls
m<' fonñe.d ' :m' no! formed
Ca
úenole > 1he C:latom in e.ach ammo acid, wh1lr R indicates the side charn peculiar to e:ich anüno 1c1d.
Figure 2
:
The hydrogen bond energy can a/so be calculated
ín t
h
e
framework
o
f
qvantvm-chem 1cal methods. Thu
s
questt0ns
such as t
o
what leve! of stabílíty
m
o
f
e
cu/
es
can be
coupled
etc
.
can be so/ved by quantum
chem1cal calculat1ons
.
DRUG DESIGN
Recently, a variety of molecular-design tech niques called drug design are applied to the development of new medicaments Rather than synthesizing a
series of compounds and meas uríng ali their act1vity, quanlum-chemical calcu
labons allow to obta1n more effcctively informa lion about the struclures and their reactions. Of course, 1t is impossible lo produce new medica
ments by basing only on the quantum-chemical calcu!atons, but such calculations unquestion ably would facllitate and assure the process of their
development.
DNA and G1:.net1c tnformations
The DNAs normally exist as a double helix and
contain genetic 1nforrnations (9) In order for the genebc informations conta1ned in the ONAs to be preserved forever and transmitted from gen eration
to generation witl1out errors. four DNA bases. adenine (A) and thym1ne (T), and gua
nine (G) and cytosine (C) play a crucial role.
The fact that these bases torm hydrogen-bond pairs stably prov1des the basis of ex1stence of our living bodies. By clarifying the distance
dependency and angle-dependency of the hydrogen-bond energy between A and T. and between G and C by means of quantum-chemi cal cafculaíions, il has
been found that the rela t1ve contiguration of bases in the DNA double hel1x corresponds to such a configurat1on that
allows A and T, and G and C to form the hydro gen bonds. Namely, the remaining part of a
DNA (sugar and phosphate group) prepares an environment in which A and T, and G and C can form the hydrogen bonds stably.
lt 1s known that the DNAs take structures whích are roughly class1f1ed mto 3 types. type A. type B and type Z The ONAs of type A and type 8 have a
double right-handed helix structure. On the other hand the DNAs of type Z consist of an ant1-clockwise helix with a zigzagged trame work of sugar and
phosphate groups. However. if we focus only on the hydrogen bonds between bases, the structure of hydrogen bond pairs are common to ali these types.
Although the sugar and phosphate groups can move freely and change the structure, the relative configuration among the bases rernain unchanged. The
DNA's global structure varíes
subtly according to the base sequence . While
Rev. Centro
/nv (Mex) Vol 4
Num
1
5 A
L
1osto
2000
protein recognizes a DNA according to the recognit1on of the funct1onal groups specific to four types of bases, 1t 1s also possible
that any deformation 1n the ONA's global structure could be a signal for lhe DNA recognit1on.
lf these bases are modified or replaced by other substances, the genetic 1nformat1ons m1ght be changed and the funct 1on of the result ing prote1n
might be affected, or in sorne cases even the requ1red protein might not be produced at ali. or no control m1ght be effective. Such a process might be
a cause of cancer. Quantum
chemistry offers a powerful tool to idenlify the
spec1fic1ty of the interactions between nucle1c acid bases as well as the interactions between nucleic acid bases and amino acids. What part of the
nucleic ac1d does protein (which controls the appearance of genetic informations of the nucleic acid) recognize and combine specifically to perform the
function? -th1s 1s one of the most important themes which the modern molecular biology 1s act1vely studying. The quantum chemical lechniques in
para!lel with experi ments are indispensable to clarify the issues.
DISCUSSION
The progress in chemistry and 1ts application fields would not be possible without understand ing lhe essence of chemical phenomena and reactions.
Such understanding can be achieved only throug h quantum chemistry. By the progress in understanding a variety of chemical phenomena it becomes
poss1ble to expect syn thes1zation of a variety of industrial products with high qual1ty. to develop an effic1ent synthe sis method, to compase new
medicaments effecllvely. to clarify the causes of cancers, etc. More irnportantly the achievement of quantum chemistry gives stimulus to the
developments of the life science fields. such as the molecular biology. and is making possible the deeper understand1ng of the essence of "life". As is
well known life sciences find also a vanety of appli cations 1n medicine, such as genet1c therapy As is expla1ned in this papcr quantum chem1slry
plays a fundamental rcle in under-stand1ng things closely related to our f1fe .
REFERENCES
(1) P.A.M. Dirac. Proc. Roy. Soc. (London). 123.
714 (1929).
(2) Schaefer. H.F. (ed.) Methods of Electronic Structure Theory, 111, vol. 3, Modem Theore tíca/ Chemist ry, Plenum Press, 1977.
(3) Schaefer, H.F. (ed.) Applicat 1ons of Electro níc Structure Theory, 111, vol. 4, Plenum Press, 1977.
(4) Segal. G.A . (ed.), Semiempirical Methods of Electronic Structure Calculation, Part A: Techniques, vol. 7. Modern Theroetica/ Chemistry, Plenum Press, 1977.
(5) Segal, G.A., (ed.), Semiempirical Methods of Electronic Structure Calculation, Part 8: Techniques, vol. 8, Modern Theroetical Chemístry, Plenum Press, 1977.
(6) K. Fukui, Theory of Orientation and Stereos election , Springer-Verlag, Berlin, 1975.
(7) Kaufmann, W. J., 111 and L. L. Smarr,Super
computing and the
Transform
ation
of
Sci ence. W. H. Freeman and Company, NY, 1993.
(8) Branden. C., and J. Tooze, lntroduclíon to Protein Structure. Garland Pub., New
York , 1991.
(9) Watson, J. O . N. H. Hopkins, J. W. Roberts,
J. A Steitz and A M. Weiner, Molecvlar Bíology of the Gene, 4th
ed , Benjamin/ Cummings Pub. Co., Calif.. 1987.
![]()
![]()
![]()
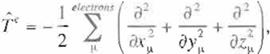 (Eq 3)
(Eq 3)
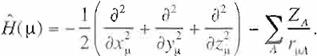 1 l ,J
1 l ,J
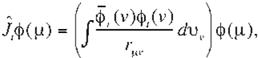
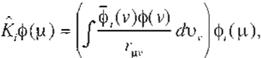
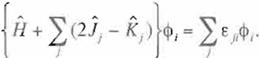
 The structures of molecules obtained by the ab initio MO method have been compared so rar with the ones obtained by experiments in vari· ous cases and
the level of reliability of the struc tures by this method (depending on the basis functions used) is now well established. Now the structures
obtained by the ab initio MO method are seldom questioned if only one is careful in choosing the basis function system. Moreover, not only the mosl
slable structure for a molecule. bul also olher structures and their relative stabilities can be analyzed by calcula tion. Although the most stable
structure can be achieved by experiments as well, it is difficult to realize unstable structures experimentally. Therefore , the ab initio MO method
can provide with the precious informations on the molecular structures of various isomers and the 1rrelative stabilities and/or the molecular
structures in the excited states.
The structures of molecules obtained by the ab initio MO method have been compared so rar with the ones obtained by experiments in vari· ous cases and
the level of reliability of the struc tures by this method (depending on the basis functions used) is now well established. Now the structures
obtained by the ab initio MO method are seldom questioned if only one is careful in choosing the basis function system. Moreover, not only the mosl
slable structure for a molecule. bul also olher structures and their relative stabilities can be analyzed by calcula tion. Although the most stable
structure can be achieved by experiments as well, it is difficult to realize unstable structures experimentally. Therefore , the ab initio MO method
can provide with the precious informations on the molecular structures of various isomers and the 1rrelative stabilities and/or the molecular
structures in the excited states.
