Control adaptable utilizando Redes Neuronal es Artificiales Polinomiales

E Gómez-Ramírez

Universidad La S alle, Jefe del Área de Ingeniería y T ecnología

<egomez@aldebaran.cí.ulsa.mx>

A. S. Poznyak

C!NVESTAV - IPN. Sección de Control Automático.

Av. IPN 2508 AP 14-740. CP 07000, México O.F, Mé x ico .

< apoznyak@ctrf cmvestav.m x >

R. Lozan o

Umversité de Compiegne

Centre de Recherches de Royaflieu BP 20529, 60205 Co mp ie g ne Cedex Fr a nce.

< Roge/l o . Lozano@hds . utc . fr>

RESUMEN

Existen en 1a literatura de Control Adaptable, diferentes procedimientos en los que es posible identificar un sistema lineal. El problema fundamental es que una cantidad importante de fenómenos de la vida real son de tipo no lineal y no es tan sencillo el modelar este tipo de dinámicas.

En este trabajo se presenta una forma de identificar sistemas no lineales utilizando las propiedades de las Redes Neuronales Artificiales y las técnicas de Algoritmo Genético en la optimización de su arquitec­ tura. Adicionalmente se presenta una técnica novedosa de control adaptable para cancelar la dinámica no lineal del sistema y colocar los polos en el punto de operación deseado. Se presenta el compor· tamiento del algoritmo para el caso lineal y no lineal y finalmente se analiza la importancia teórica y operacional de estas técnicas.

Palabras clave: Sistemas no lineales, Redes Neuronales Artíficíales, Algoritmo Genético. Arquitectura, Control Adaptable.

ABSTRACT

In Adaplive Control Theory exists differents procedures to identify a linear system. The fundamental problem is that in the real world many systems are not linear and it is not easy to obtain the mathematical model.

In this work. an identification procedure for a non linear system is presented using the properties of Arti· ficial Neural Networks and Genetic Algorithm to optimize the architecture of the network. A new technique of Adaptive Control to cancel the non linear dynamics of the system is proposed to set the poles of the system in a desire posítion. The behavior of the algorithm for the linear and non linear case is presented with the analysis of the theoretical and operational importance of these techniques.

Keywords: Non linear system, At1íficíal Neural Networks. Genetic Algorithm, Archítecture, Adaptive Con­ trol.

INTRODUCCIÓN

Para aplicar un controlador es muy importante

conocer la dinámica del sistema. Por esta

razón es necesario identificar Je la mejor forma posible el modelo matemático de la planta o al menos conocer la relación entre variables inter-

nas, salidas y entradas. Actualmente existen

Rev. Centro ln v. (Mé x ) Vo l . 4 . Nurn . 15 Agosto 200 0 17

-

alternativas del área de Control Inteligente (1) que intentan sustituir este paso por el conoci­ miento de algún experto y modelar ciertas rela­ ciones de la dinámica. Específicamente la lógi­ ca difusa (2) por medio de reglas mapea este conocimiento para encontrar cuál es la relación de control para cada caso. También existen otras herramientas como las Redes Neuronales Artificiales 3} que pueden aprender la dinámica de la planta e inclusive la de un controlador que modifique la respuesta de la planta a ciertas caracter ísticas deseadas.

Estas técnicas de aprendizaje de la dinámica de un sistema han competido y compartido campos y algoritmos con el área de control adaptable (4). Esta área ha tenido gran auge por ser una aproximación sistemática para el ajuste automático de los parámetros del contro­ lador en tiempo real. Este ajuste puede depen­ der del conocimiento de la dinámica. de un modelo identificado de la planta. o simplemente

puede adaptarse a los cambios del sistema

dependiendo de su interacción con el medio.

En este artículo se presenta una combinación de Redes Neuronales Artificiales Polinomiales con técnicas de control adaptable y su uso para sistemas lineales y no lineales.

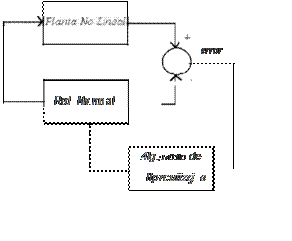
CONTROL ADAPTABLE

Las incertidumbres y variaciones de los pará­ metros de procesos hacen que el desempeño de los sistemas de control se reduzca. Una de las alternativas para reducir estas perturba­ ciones y oscilaciones sobre las variables de control es la retroalimentación. De tal forma que sí es posible encontrar el valor de estas pertur­ baciones, alimentan al controlador para ser can­ celadas y obtener un apropiado comportamien­ to de nuestro control. Un concepto necesario para cuantificar el buen funcionamiento de un sistema es el Índice de Desempeño (ID). Este indicador es una medición del comportamiento del sistema; se compara con el ID deseado y la diferencia es introducida al mecanismo de adaptación. Este mecanismo actuará sobre los parámetros del controlador para modificar el desempeño del sistema.

18

Definición 1

Un sistema de control adaptable mide cierto ID del sistema de control utilizando las entradas, los estados. las salidas y las perturbaciones conocidas. De la comparación del ID medido y del deseado, el mecanismo de adaptación mo­ difica los parámetros ajustables del controlador ylo genera un control auxiliar para mantener el ID del sistema de control lo más cercano posi­ ble al deseado.

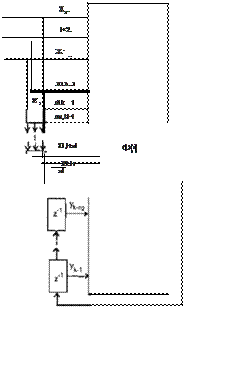
Un Sistema de control adaptable puede ser visto como un sistema jerárqu ico de dos niveles donde:

• El Nivel 1 es un Control Retroalimentado Directo

• El Nivel 2 es el Lazo de Adaptación

En la práctica frecuentemente se tiene un ter­ cer nivel de supervisión, el cual decide si las condiciones cumplen con las caracteristicas de operación del lazo de adaptación.

Existen varios esquemas utilizados en Con­ trol Adaptable como:

• Control Adaptable de Lazo Abierto

• Control Adaptable Directo

• Control Adaptable Indirecto Control Adaptable de Lazo Abierto

Este Mecanismo de control es una simple tabla de relaciones entrada-salida almacenada en la computadora. la cual define los parámetros de control para un conjunto de mediciones del medio. Esta técnica considera la existencia de una relación definida entre algunas variables que caracterizan el medio y los parámetros del modelo de la planta. Utilizando esta relación es posible reducir los efectos de la variación de los parámetros sobre el desempeño del sistema, modificándolos dependiendo de las condi­ ciones.

R 1>< ('ntrc In (M .,1 .t 4 N 1m f .

Artículo

Control Adaptable Directo

En este control los parámetros dependen direc­ tamente de la especificación del desempeño deseado del lazo de control. Este desempeño puede depender de un modelo de referencia con las características dinámicas deseadas . De tal forma que el diseño del controlador debe cumplir que:

• El error entre la salida de ta planta y la salida del modelo de referencia sea igual a cero para condiciones iniciales idénticas

• Cualquier error inicial desaparezca con cierta dinámica.

Cuando no se conocen los parámetros de la planta o éstos son variantes en tiempo, y se desea mantener el 1 D deseado, es necesario utilizar un esquema de control adaptable cono­ cido como Control Adaptable con Modelo de Referencia (Model Reference Adaptive Control, MRAC). Este esquema se basa en la obser­ vación de que la diferencia entre la salida de la planta y la salida del modelo de referencia es una medición entre el desempeño real y el deseado. Esta información es utilizada por el mecanismo de adaptación para directamente ajustar los parámetros del controlador en tiem­ po real para forzar asintóticamente el error a cero. Este modelo es el prototipo básico del Control adaptable directo. En la Figura 1 se puede observar el diagrama para un sistema lineal aplicando un control adaptable directo.

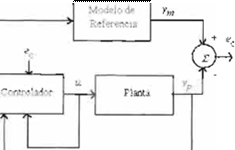
Frgura 1 Control Adaptable drre..,t o

Los esquemas de Control Adaptable Directo se obtienen principalmente de las siguientes dos formas:

R t • V Cenrm lnv (Méxl Vol 4, Ntirn 15 Agosto 2000

Definiendo una ecuación para una señal de error (error de adaptación), la cual es una función de la diferencia entre los parámetros sintonizados del controlador y los paráme­ tros actuales

• Utilizando una aproximación de un control adaptable indirecto con un prediclor adap­ table de la salida de la planta reparametriza­ da. en términos de los parámetros del contro­ lador, y forzando la salida del predictor adaptable para seguir exactamente la trayec­ toria deseada.

Control Adaptable Indirecto

Este esquema es denominado indirecto debido a que utiliza los siguientes pasos:

1. Estimación en línea de los parámetros de la planta y posteriormente,

2. Cálculo en línea de los parámetros del con­ trolador utilizando la estimación del modelo de la planta.

Este sistema de control ofrece una gran va­ riedad de combinaciones de leyes de control y de técnicas de estimación de parámetros, debido a que es posible escoger en principio cualquier sistema de estimación de parámetros con cualquier estrategia de control. En la Figura

2 se puede observar el diagrama correspon­ diente.

El problema esencial de un esquema de con­ trol adaptable es el asegurar la estabilidad del sistema de lazo cerrado. Para esto sería nece­ sario un profundo y complejo análisis del contro­ lador. Esto se puede reducir si se cumplen cier­ tas propiedades.

Uno de los esquemas de control adaptable indirecto mas utilizados es el de Colocación adaptable de polos. En las siguientes secciones se describirá esta metodología para:

·Sistemas lineales de fase mínima.

• Sistemas lineales de fase no mínima.

19

A rtfculo

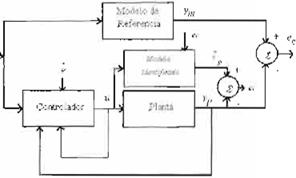
Figura 2 Control Adaptable Indirecto

Control de Sistemas Lineales de Fase Mínima en Tiempo Discreto.

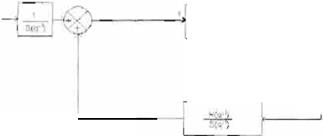
Considérese el siguiente sistema como una entrada una salida (single input single output. SISO):

(Ec. 1)

donde: xk es la entrada, Yk es la salida, q-1 es el operador de retardo, des el retardo y

A ( q -.1) = 1 + a1q-1 + ....+ ª"zq _,,,,

B( q -1) = bo + b1Cf-1 + ....+ bll¡q-111

(E c. 2)

donde n2 es el número de polos y n1 el número de ceros del sistema . B(q-1) es estable con b.

Considérese también que se cumple la siguiente relación:

( Ec. 3)

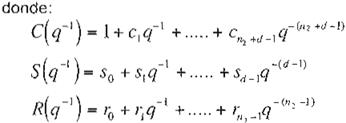
(Ec . 4)

20

.Con esta identidad polinomial se pueden cal­ cular los valores de S(q- 1) y R(q- 1) para un valor determinado de C{q-1).

e( -1) ;

Si se calcula q ) hd

e(q-1)Y = A(q-1)s(q-1}y + q.d R(q .1}

c(q-l)Y = s( q-' )A( q-1 )y + q-d R(q-1)

e(q-i )Y = s(q-i)[q- dB(q-1 )xJ+ q- d R(q-1 )

c(q-').v = q-.1[s( q-1 )B( q-1 )x + R(q-')}= q-dy*

(Ec 5)

(Ec. 6)

y si C(q-1)= 1 entonces

(Ec. 7)

Esta ecuación describe el comportamiento de la salida del sistema en el tiempo k+d.

Figura 3 Esquema de Control Adaptable para Sistemas de Fase Mínima

Control de Sistemas Lineales de Fase no Míni­

ma en Tiempo Discreto.

Considérese de igual forma que en el caso de fase mínima el siguiente sistema una entrada una salida:

Rev. Cen(ro ln v . (Méx) Vol. 4 Núm 15 Agosto 2000

Si se propone la siguiente ley de control:

(Ec. 8)

donde: xk es la entrada, Yk es la salida . q- 1 es el operador de retardo, d es el retardo y

A(q -1) = 1 + a,q - 1 + .... + ªn.q-"2

se tiene que:

(Ec. 13)

( E c. 14)

B(q· 1 ) = b

+ b q- 1 + .... + b"/J -111

donde n2 es el número de polos y n 1 el número

1 1

0 1

(Ec. 9)

!'.4 tlj 1

de ceros del sistema. B(q-1) es estable con b0;t.O.

Consicérese también que se cumple la siguiente relación:

e(q- ) = A(q-I )s(q -\ ) + s( q-1 ) R( q-1 )

Figura 4 Esquema de Control Adaptable par a Sistemas de Fase no Mínima

donde:

(Ec. 10)

Control Adaptable con Redes Neuronales Artifi­ ciales

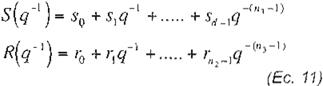
Con es1.a identidad polinomial se pueden cal­ cular los v3lores de S(q-1) y R(q-1) para un valor

determinafo de C(q- 1) donde A(q- 1) y B(q-1) son primos en :re si.

e(q-1 )y = A( q-1)s(q-1 )y +B (q-1 ) R(q · 1 )

c(q-1 )y = s(q-1 )[scq-1).x]+s(q-1 )R(q-1 )

e (q-l))' = B (q-l)[s(q -l )X +R (q_, )y]

(Ec . 12)

Rev. Centro lnv. (Méx) Vol. 4, Num. 15 Agosto 2000

Como se mencionó anteriormente, en el control adaptable indirecto es posible utilizar cualquier algoritmo que cumpla con ciertas condiciones para la estimación del modelo de la planta. Las teorías y técnicas conocidas como RNA han demostrado su gran capacidad para este tipo de tareas. La caracteristica más significativa de las RNA es su habilidad para aproximar cualquier función no lineal. Esta habilidad las ha colocado como una herramienta muy útil para el modela­ do de sistemas no lineales, la cual es muy importante en el diseño de controladores para este tipo de dinámicas (5)(6). Funahashi. Hornik y cols., Cybenko, Cotter (7-10) y Blum y U, uti­ lizando el Teorema de Weierstrass como base. demostraron que una función continua puede ser aproximada utilizando una red neuronal estática con una capa oculta. Otros autores han utilizado el teorema de Kolmogorov (11) para demostrar las capacidades de estas redes. Modelos estáticos y dinámicos han sido pro­ puestos para identificar y controlar sistemas dinámicos con diferentes arquitecturas.

21

Arrículo -- 1.1

Un esquema muy utilizado para la identifi­ cación de una función no lineales el que se pre­ senta en la Figura 5.

Y( i)

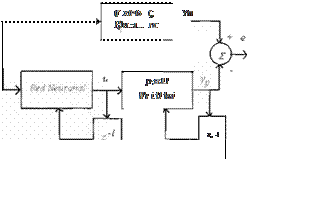
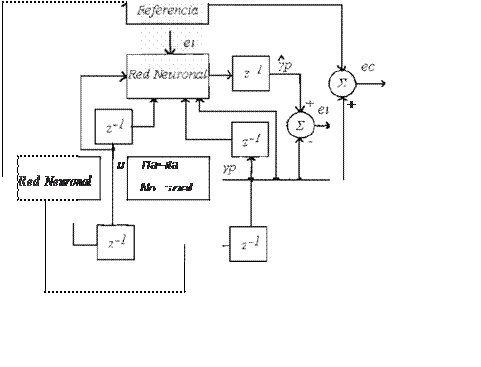
De forma similar a las secciones previas es posible desarrollar algoritmos de Control Adap­ table con RNA. En la Figura 6 y Figura 7 se pre­ sentan dos esquemas de control adaptable directo e indirecto utilizando RNA (12)

r

Fi gura 5 Esquema Genera l de A pren di zaje p ara l a Ap r oxim a ció n d e u na Func1on UtTlizal1(10

Redes N euro n ales

llfocidc. d

r

F i gura 6 Esquema de Control Adaptaole Dire ct o

de •ma Plante no Lmeal Ut1/1zando RNA

)'l.'S

Figur e 7 Control Adaptable Indirecto Utilizando R.f\JA

L 2 Re v Ce ntro lnv o ' >A<:X) Vol .: Num 15 Ag 1 200ó

-- - - - Arlículo

Como se puede observar la estructura es muy similar a la utilizada para el caso lineal y en lugar de las ganancias lineales se coloca una red neuronal artificial.

Los bloques con z· 1 representan los retardos de la señal. Uno de los algoritmos más utiliza­ dos para el entrenamiento de estas redes es el backpropagation . Como se puede ver en las fi­ guras los datos de entrenamiento entrada-salida son generados directamente del sistema dinámico. En (12) se puede consultar la forma en que pueden ser aplicados para distintas plan­

Descomponiendo f() como un polinomio de grado L se obtiene la siguiente representación:

''v

y( t) = :¿s¡x¡(t) + f.(t.8 )

i-1

( Ec. 17 )

donde:

l

n 0 = _¿ n¡ ; '1o = l,

i= O

tas no lineales

n, = 1 _ 1 ( n >' + n 11

+ n e + i - 1 ) / i

Modelos NARMAX Teoría

n

Algunos autores han considerado a los modelos NARMAX (13)(14) como una alternativa efi­ ciente para la identificación de sistemas dinámi­ cos no lineales (15)(16). En esta sección se describe lo que son estos modelos por la impor­ tancia que tienen en el área de identificación y por su similitud con las redes neuronales (17),

i = 1,...,L

(E c. 18 )

(Ec. 19)

en especial con las RNAP.

Considerando algunas suposiciones un sis­ tema de control no-lineal discreto estocástico puede ser descrito mediante el modelo NAR­ MAX (18):

y(! - J), ...,y(t- nv).u(t - 1),. ]

Como se observa puede haber varias repre­ sentaciones para un mismo sistema . Existen algunos casos particulares para representar f(') utilizando el modelo bilineal (1 modelo polino­ mial, etc.. Como se puede observar al igual que en RNA, es necesario definir las dimensiones máximas del modelo.

y(t) = f [ ...u(r - n,,).e(r - t),....,e(1- 11,)

+ e( t)

(Ec . 15)

Este modelo fue propuesto por Leontaritis & Billings y puede tener una gran cantidad de re­ presentaciones, cada una con sus ventajas y desventajas dependiendo de la aplicación.

donde y(t), u(t) y e(t) son la salida, entrada y

ruido del sistema respectivamente; ny, nu, ne son

los órdenes o valores anteriores máximos de la salida. entrada y ruido. En este caso e(t) se supone que sea una secuencia blanca y f() es alguna función no lineal. Este modelo se le denomina NARMAX por su seme1anza con el modelo lineal:

n, "v

y( k )= a 0 + :¿a,y( k - i) + 2b;u(k - i)

i=l i= I

(E c. 16)

R v. G.?11 o h ' íMex) Vol 4 Núm. í 5 Agosto 200!';

Los coeficientes de la Ec. 17 se obtienen por el método de mínimos cuadrados.

RED NEUl ONAL ARTIFICIAL POLINOMIA L

La historia de las RNA comienza con el trabajo de McCulloch y Pitts (19) planteando algunas ideas para modelar el sistema neuronal. Estos modelos biológicos han cambiado con los nuevos avances reportados en las neurocien­ cias y la tecnología. Actualmente. se sabe que las conexiones sinápticas no solamente pueden

Artículo

ser modeladas mediante una suma de la pon­ deración de las entradas (20). Los resultados muestran que algunas neuronas pueden modu­ lar, potenciar y ponderar la respuesta de otras neuronas (21). Esto significa que el modelo por neurona pudiera considerarse como una relación de multiplicación o potenciación. En la literatura se pueden encontrar algunos modelos que aprovechan estas ideas como: Las Redes Neuronales Polinomiales (RNP}, (Polynomial Neural Networks, PNN) (22). Redes Neuronales de Orden Mayor (Higher Order Neural Net­ works. HONN) (23) y modelos con interconexio­ nes no lineales. Este tipo de representación no es exclusiva de las RNA y se pueden consultar modelos similares matemáticamente en otras áreas. por ejemplo: el modelo NARMAX (24)(25), el Método de grupo para el manejo de datos (Group Method of Data Handling (GMDH) (26)(27) y las Aproximaciones Polinomiales (28)(29).

El modelo de RNAP propuesto puede ser descrito como·

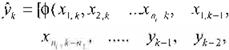X 1.k-l' ....

: .,111

····Yk-n )] ""

( E c . 20)

;

donde: E -:J\ es el estimado de una función, es decir la salida de la red, (x,y)E '.R es una fun­ ción no lineal, X1E X son las entradas, 1= 1,...,n1 n,=número de entradas. Yk-/= Y son los valores

anteriores de la salida.1=1,..,n2, n1 el número de retardos de la entrada, n2 el número de retardos de la salida, X, Y son conjuntos compactos de '91.

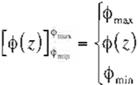
La función no lineal cp{z) está dada por:

<f>( z) <f> m

<f> m1n < <j>(z) < <1>m3x

<!>(Z } S <!> mio

Para simplificar el manejo de la notación en las ecuaciones se va hacer un cambio de varia­ ble de tal forma que:

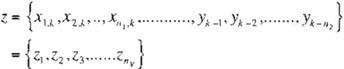
(Ec . 22)

donde: nv es el número total de elementos en la descripción z. es decir, el número total de entra­ das. valores anteriores y valores anteriores de la salida:

(Ec 23)

Entonces la función if>( z} t= ({Jp pertenece a una familia de polinomios <Dp que pueden ser repre­ sentados:

<l> P ( Z. l •l.1····· · Z",, ),.

4>(z ) :<j¡(z) • ll0(z,,z2 ,...•,<,,.) + a1 (Zt • .:i ······z,., )}

{+a!(zl,Z1··· ,z,,_).. ·· . + a,/ z1 .Z¡ •...., z., )

(E c . 24)

El subíndice p es la potencia máxima de la expresión polinomial, en tanto que los términos (),(z1> z2······z•,) son polinomios homogéneos de

grado total i, para i=O,.. ,p. Cada polinomio homogéneo puede ser definido como:

a 0 ( : , ,2-, .... . z _ ) = w0

1 1 1 1 1

a (z ,z,,...,z ) = w .- ·w ,z, + ... + w Z

.. n., •' • • ' ' ·'1-. "v

ª 2 (z ,, Z2, ...,z,._ ) ,,.. w2 ,z + w2.2Z1Z2 ..;.. w2,3Z1.Z + ....

n, ' ·• 1

... +z¡Z +...z! + ...Z2ZJ ... + w, V z2

W¡_,ziZ; +w,_5Z 1Zi Z + l\i3.6ZJZ +

+...z3 + ..z 2z, + ..z,z + ......J.. 11·, •• .z3

2 ! .J - 'l IJ\

ap (z, , 72.• ..· - ) - wp,1 zP) + 'V,,.2'-7p ·1z2 ,'- •..

(Ec. 21)

donde <Pmax and 1Pmin son los límites máximo y mínimo respectivamente .

1""· - r

...+ \VP .r,z:.

( E c. 25)

24 Rev C entr o l nv (Méx} Vol. 4 , Nllm . 1 5 Agost o 2000

Artículo

donde wíj corresponde al peso asociado a cada neurona. El término w0 corresponde al input bias

mada de Fourier, es decir, obtiene el promedio de la señal que se quiere estimar. El polinomio adz) corresponde únicamente a la ponderación

lineal de las entradas. De a2(z) a ap(z) se repre­

entradas correspondientes y las relaciones de potenciación.

Como se puede observar, los términos utiliza­ dos a partir de z( permiten al algoritmo resolver

el problema de paridad bidimensional que tenía el perceptrón. Esto es análogo al efecto de tener varias capas en una red neuronal tradi­ cional.

El valor N¡ corresponde al número de térmi­ nos de cada polinomio homogéneo:

'¿i ,

fl. n -111 - s 1

N0 = l, N 1 = nv , N2 = :¿i,N 3 = '}:

i=J s, =0 i= J

( E c 26)

N p '= • .." nvi1"f 1¡

<,,_1 0. si =O s,=O i= I

'--·---,---

p-1

La dimensión Nq) de cada familia r.t>p puede ser obtenida de la siguiente forma:

p

N <t> = _¿N,

icO

( Ec. 27)

Rev Centro lnv (Méx) Vol 4, Núm 15 Agosto 2000

y "

Figura 8 Esquema de RNA P

El modelo ARMAX es uno de los algoritmos más comunes para identificar sistemas dinami­ ces lineales. La RNAP con el parámetro p=1 puede ser considerada como un modelo ARMAX y con p 2 como un modelo NARMAX. Una de las ventajas de RNAP, es que obtiene la representación óptima y es posible identificar la parte lineal y no lineal de un sistema dinámico. En las siguientes secciónes se describe esto en detalle.

Aprendizaje de RNAP

Para introducir el aprendizaje en RNAP es necesario, primero, introducir algunos concep­ tos que serán utilizados en este artículo.

Definición 2

El error de aproximación de RNAP se define

como :

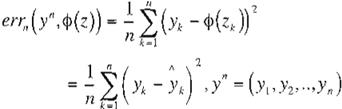
( E c . 28)

25

\111i 1 ·1til1- - -

--_ - --- - -

donde Yn es la salida deseada, q>(zk)e <l>p y n es el número de puntos.

Definición 3

E l error óptimo está definido como:

opterrn( y' ',<j>( z.)} = minen;,(y", cj>(z))

81>,

donde W = { wJ> w ,.....,wN . }

2

f son los pesos

de RNAP, Wb es un vector binario, y N<I> se obtiene utilizando la ecuación 26.

Definición 5

E l producto .* se define como.

= en (y'',<P,:( z))

W .:;,: W'.T =

w if wb = 1

IJ J

(Ec 29)

do nd e cp,;(z ) E< )P es la estimación óptima de

¡, { O

1if ' w '.) = O

j

(Ec . 32)

/l.

Definición 4

Por e 1 emplo , para W y Wb co m o:

w ,, w,2 Wn

La RNAP lf>(z) E c/JP aprende uniformemente la salida deseada co n precisión e si

W = W 2 1 Wll W23

w " o w,,l

W31 1\., W33

W,, = [1 o t]

en;,(/,<ji(z)) - err( y' ' ,<\>:,(z)) > E E > O

Después de describir estos conceptos ahora el problema del aprendizaje de RNAP consiste en encontrar la estructura de <P E <l>p(z) que veri­

fica esta desigualdad.

w ; .

En la siguiente sección se aplica el uso de algoritmo genético para obtener el valor del

arreglo Se presenta un algoritmo que

obtiene la arquitectura óptima de la red me­ diante el uso de AG (30). Para lograr esto defi­ nase un vector de componentes M(z): utilizando la simplificación de (22}:

_2 z.1 7 2z 7P }

• • •) '1V ) 1 1"i 2 " •••••' "ro•

(Ec 30)

Entonces la función no lineal E CJ>p(z) descri­ ta en la ecuación 24 puede ser representada como:

<I> = {W .M{z)}donde W = \\i." \\·;,' .'tlw E{0.1}

(l c. f )

26

W . * w : = w21 o H'23

W31 o w'..'.'.1

y para el caso vectorial:

[w1 11'¡ W¡ 11'4) •[1 0 1 of = [wl 0 hj o]

La ecuación 31 representa que iJ> solamente tiene términos específicos de <Pp que pueden

ser seleccionados por Wb de tal forma que la estructura óptima de RNAP </>* puede ser calcu­ lada como:

(p*(z)(=):w· ' M ( z )°" = .:w.* (w;,},M(z)·,

6

= i W ,Af (z).* (wr )* "

(E: c . 34)

Rov CerrltU In (Mex) Vol 4 Num 15 ü,g<»to 2000

:=::> opr en;,(/,cj>(z)) = opt en;,( / .(( w")' ,M( z) ))

W' W

(Ec . 35)

Utilizando las ecuaciones 31a 35 el problema de aprendizaje para una estructura específica puede ser representado por un problema de optimización con los siguientes dos pasos:

/

min minen)/ <t>( z))I

\'.', IVE:l\ ' Wb

( Ec . . .,

De esta forma el problema de aprendizaje puede ser traducido a obtener la óptima estruc­ tura de RNAP utilizando AG.

ALGORITMOS GENET!COS

A lgoritmo Genético es un modelo de opti­ m1zac1ón que se encuentra basado en algunos de los mecanismos de evolución que se obser­ van en la naturaleza. Este modelo de compu­ tación genética puede ser implementado con el uso de arreglos de bits o caracteres que re­ presentan los cromosomas. Aun cuando exis­ ten muchos trabajos acerca de cadenas de lon­ gitud variable y sobre otras estructuras, la

donde

err,, (/',<P(z))1w. es el error definido en

mayoría del trabajo con Algoritmos Genéticos

la ecuac1ón 28 para un valor determínado de

Wb.

Los valores del parámetro W pueden ser obtenidos utilizando el método de mínimos cuadrados (31):

Wl111 = argmin en;,( y'',cj>( z ))'

b wen·" w,\

W lw . = r·''!yk ( M 1,( zi )) M) zi:) = M.* w[

k=I

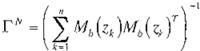
(Ec 37)

o en su forma recurrente :

(wl.:,), = ( w1.,L, + f',M (zj [r; - (wlw,LM,(z, f ]

r• .r . _ r , _ ,M, (rS M(z. )r; ·

1 + M (l,).r,_1M,,(<:t )

(Ec. 8 )

está enfocado hacia cadenas de longitud fija, si

no es manejado de esta manera, el Algoritmo de Evolución que se está considerando será Pro­ gramación Genética, la cual se enfoca hacia cadenas de longitud variable (32,33).

Cuando se implementa el Algoritmo Genéti­ co, usualmente sigue el siguiente ciclo (34,35)·

Generación de una población inicial de forma aleatoria.

Evaluación del más apto o alguna función objetivo de todos los individuos que pertenecen a la población.

Creación de una nueva población debido a la ejecución de operaciones como recombi­ nación (crossover) y mutación sobre los indi­ viduos de donde el más apto o el valor mejo­ rado fue medido.

• Eliminación de la población original e iteración, utilizando la nueva población hasta que el criterio de terminación sea cumphdo o se haya llegado a cierto número de generaciones, sin haber completado el objetivo planeado.

Para este caso N=N<D y el espacio de búsque­ da tiene dimensión 2N. En algunos casos con­

' ¡

.

(

r. ,-,

-

... ... o

e c.

·' < c..

siderando un valor fijo de p, n1, n2 es muy proba­

ble que no se requiera de todos los elementos

¡, (

.;.

de ef1(z) y como se describió en la sección ante­ rior es posible seleccionar qué elementos se requieren para obtener una arquitectura o estructura óptima.

Rev C.;-nlro JllV (M<-J. ) Vo l i. No11n 15 Agosto 2000

Figura 9 Etapas Canónicas del Algoritmo

Genético

2 7

A rt í<'11/ o

El distinto tipo de operaciones que se hacen sobre las cadenas o cromosomas que son manipulados dentro del AG son llamadas ope­ radores, en este trabajo se utiliza eloperador de recombinación sexual, la mutación (36) y otros procesos especiales que son llamados agregar padres (26). Las siguientes secciones describen estos procesos en detalle.

Recombinación

El operador de recombinación se caracteriza por la combinación de material genético de los individuos que son seleccionados en función del buen desempeño (función objetivo) que tuvieron en comparación con el resto de los individuos o "padres" que conforman la población. Existen algunas variantes de este operador (37), que

c ( , 11 , ) E l.B" ' '"b es el operador de recom­

binación y puede ser definido como la combi­ nación entre el conjunto de padres consideran­ do el número de intervalos n1 de cada individuo y el número de hijos ns por lo que:

11 = n n,

.• p

(Ec . 39)

Para mostrar cómo es que puede ser aplica­ do el operador de recombinación,considere que F9 se forma con np=2 y n1=3. Esto significa que

se divide el arreglo en tres secciones y se

denomína a cada sección como a, y b¡ respecti- vamente para i=1,.., n1• Si:

puede ser determinado por el número de puntos de recombinación que serán considerados para la generación de una población, el número de padres involucrado para la generación del lina­ je, etc. Es obvio que si el número de puntos de recombinación se incrementa, el número de individuos que conforman el linaje. será también mayor.

F = [ª1

b

1

b 2 ]

a, G.i ª3

a, ll:? b

a, h2 ª3

a, h2 b3

:::::> c(Fs,3) =

00

1

b, U3

b , G.i h .,,

b, b 2 ª3

b, b 2 b 3

1

Figura 1 O Operado r de Rec ombinación e n un Punto .

Para explicar la recombinación multipunto empleado. considérese que e JB"''"'b es

el conjunto de padres de una población dada donde np es el número de padres de la

población en la generación g y nb es el número de bíts del arreglo (cromosoma), g=1,.. ,ng; y ng es el número total de generaciones.

28

Es importante notar que con este operador los padres Fg de la población g se incluyen en el resultado de la recombinación.

Mutación

En el operador de mutación, sólo se niegan algunos bits que son seleccionados en forma aleatoria por medio de un factor de probabilidad P m; en otras palabras, tan sólo se varían los

componentes de algunos genes. es decir, se modifican los alelos. Este operador es ex­ tremadamente importante , ya que permite ase­ gurar que se mantenga la diversidad dentro de la población, la cuales básica para la evolución (38,39).

Rev Centro 1m · , (Méx) Vol 4, Núm . 15 Agosto 2000

o

Proceso de Selección

n

El Proceso de Selección s9 calcula la función

objetivo 0

9

que representa una función específi­

\, ..?

ca que se quiere minimizar y se seleccionan los

mejores 1nd1viduos nP de A9 talque:

Figura 11 Operador de Mutación

•

Este operador M : IE/ 1:xri. ----+ /8 11'x 11

cam­

Entonces:

( Ec. 42)

bia con la probabilidad Pm la población gene­

rada por el operador de recombinación en la siguiente forma :

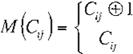r s; P. n

r > P.n

(Ec. 40)

donde rE U(O, 1) es una variable aleatoria e,

i=1...,ns; j=1, ...nb; y ff7 es el operador x-or.

El operador de mutación asegura que la

(Ec. 43)

Note que los mejores individuos de la genera­ ción g pueden ser obtenidos por el siguiente operador:

( Ec . 44)

En resumen el Algoritmo Genético puede ser descrito por medio de los siguientes pasos:

1. Para la condición inicial g=O seleccionar en

probabilidad de encontrar cualquier punto en el espacio de búsqueda nunca sea cero y evita que se alcance un mínimo local.

Agregar Padres

forma aleatoria A 0, tal que

2. Calcular F 1= So(Ao)

3. Obtener Ag

4. . Calcular s9

A o E IB"' "'

En esta parte sólo se agrega F

9

al resultado del

5. Regresar al paso 3 hasta que el número máximo de generaciones es alcanzado o

proceso de mutación, entonces la población A9

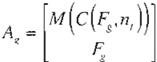en la generación g se puede obtener como:

uno de los individuos de s9 obtiene el míni- mo valor deseado de o .

9

Cabe hacer notar que A

9

(Ec 41)

tiene los mejores

Elempleo de Algoritmo Genético es especial­ mente útil cuando se tiene gran cantidad de posibilidades en elespacio de búsqueda y no se posee información acerca de cómo obtener la solución óptima para un problema especifico. Para este caso. la aplicación de la teoría es

_

individuos de A9 1 ya que se agrega F9 en este procedimiento. Este paso y elanterior aseguran la convergencia del algoritmo.

Rev. Centro lnv (Méx) Vol 4 , Núm . 15 Agosto 2000

automática si se considera a VV'.' como el

h

arreglo buscado. El problema de aprendizaje puede ser trasladado para obtener la estructura óptima de PANN usando AG. Los pasos de AG

modificados pueden observarse en la siguiente tabla 1.

· A 1ilíiw fo .-- - ---;-

Tabla 1 Pasos de AG y 4G en RNAP

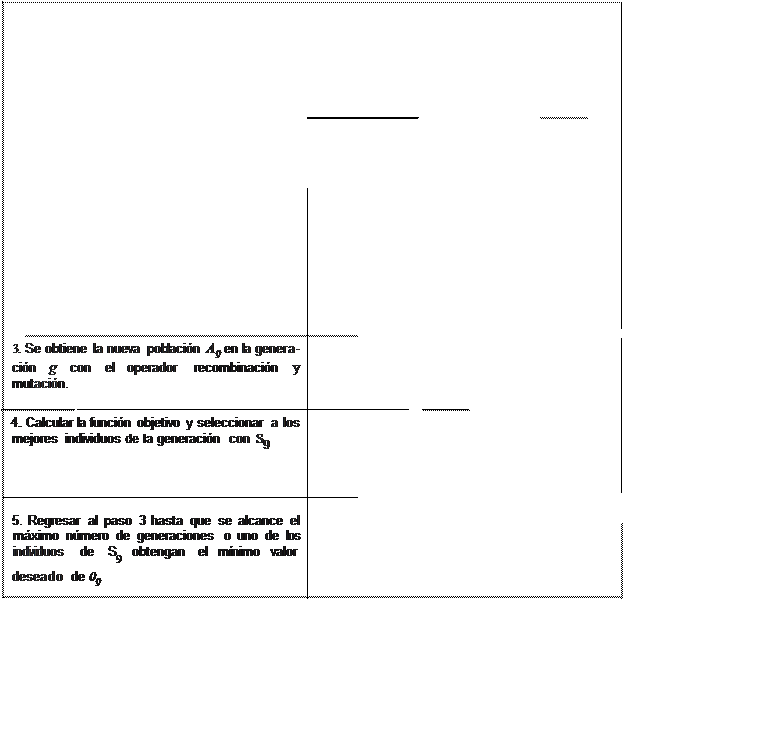ALGORITMO GENTlCO ALGOR ITMO GENÉ'.TICO EN RNAP

2.2. Se calcula

3. Se obtiene la nueva población Ag en la genera­ ción g con el operador recombinación y mutación.

-

4. Calcular S9 con la siguiente función objet ivo

5. Regresar al paso 3 hasta que se alcance el

máximo número de generaciones o uno de los individuos de s9 obtenga el mínimo valor deseado

de 0

9

El error óptimo en ta generación g puede ser

donde W¿$,

es el mejor individuo en la genera­

obtenido por:

(

opT e n ) ::::. mi, err (.v·)(w')I . .M(z)))

lr :i;: . ' i , """i.r ,, \ n,,

ción g, es decir, la estructura óptima de la RNAP en ese momento, se puede reescnb1r el error de aproximación como:

Teorema 1

Def ini endo

(Ec.1 5)

er r(J'' . <l>) z ) ) = - 1;;

" (y, -¡,w, M( z ). *(W,:)r¡\):

(Ec 47)

YV;. S , ( A , .1)

30

(Ec 46)

donde yn es la salida deseada, ¡/J (z) e <PP es la representación óptima en la generación g , y

9

Rev Centro lriv (Mr:.<i Vol 4, Ncrn. 15 .a.wsto 2000

W lw = arg min err,,( l' ,Q>(z))I

Para simplificar la notación se utilizará:

' WEffiN W"' Wl

Si Pm>O entonces RNAP aprende uniforme­ mente la salida deseada de tal forma que:

t::..

8

:= err f! - opterrK

(T2))

<l>g E (/JP puede ser descrita como:

(Ec . 48)

ó. ·= err- +1 - err ;: +errg - opten-¡;

H .

;¡•1 g

ó = ó +en·8 +1 - er,,S

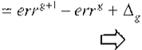
(Ec 49)

Debido al progreso de agregar padres y el de mutación

=

ó + errg- I - errg- 2

g-1 ¡;-2

ti , = 110

+ err 1 - erro

(Ec.50)

Comentar io 1

(Ec 51)

= ó.0

*

- '(err* - err *+1 )

f:'o

(T3)

Para casos prácticos, el Teorema 1 puede escribirse utilizando la Definición 1 como:

Si Pm>O entonces la RNAP aprende uni­ formemente la salida deseada con precisión e en un número finito de generaciones ng si:

Definase·

a k := err k - errJ.?l >- o

(T4)

3

) '!'. f' {e r r(y. <jl (z) - op ien{ y,<P( d)> s)} = O e> O

Observe que para la prueba del teorema es suficiente probar que:

Demostración del Teorema 1 Definase:

(Ec . 52)

Sn(c.0 ) =

"

ak(w ) = S,,_ (w) + a,,(w )

(TS)

0

6,,:= err( y, cp .,.h))- opterr( y.cps (z))

Re•1 ( entm 1n v. (Méx) Vol 4, N(im f ; Ago.5fo 2non

(T1)

¿ 1

k - 0

(T6)

31

A rt íc11 lo

Para probar (5) es necesario probar que:

y considerando

Entonces

(T7)

entonces:

E{s,,(w)i ,,_, }º·s,,_ 1 (w) + E{a,.(Cl))l .J

(TB)

donde gn-1=a(ooo1,821 ...8n-1J es la sigma-81gebra generada en el proceso correspondiente y w es un evento aleatorio. Se tiene :

f a /w )dP( w f5,,_ 1) =J.,.·<>n<w )dP Cw Pn_,)

+f....a.« éJ .,(e.o)dP(wl -i)

a s.

.'. ¿P,, = co

= I

f a ,.(w )dP(w ,,_ 1 ) :2::

L.a. ( o.,(w)dP(w ,,_1)

EP{ a ,, :2:: n-i} = cP,,

(T9)

(T10)

:::::> hm err( y,<jJ ( z)) = opterr( y,cp( z ) )

s- .,o (w ) '

Q. E. D. ..

Como se puede observar la representación de RNAP puede ser considerada como un caso particular del modelo NARMAX. Por lo tanto, también es posible aplicar la metodología desccita en la sección anterior utilizando AG para este tipo de modelos.

Es importante recordar que para una variable aleatoria r(w) se cumple que el operador mutación es igual a:

r(w) s P,,,

r(úl) > P.n

y

utilizando:

T 1 ¡; IH

P{ A = A } = O VP > O

32

CONTROLAOAPTABLE CON RNAP

En esta sección se describirá la forma en que una RNAP puede ser implementada para su aplicación en control adaptable de sistemas no hneales utilizando un esquema de control adaptable indirecto.

El modelo de RNAP descrito en el capítulo anterior puede reescribirse como:

(Ec. 53)

donde (x) y lf>( y ) representan los términos

Rev Centro lnv. (Mex) Vol 4, Núm. 15 Agosto 2000

lineales de q>(z) Estos términos son eqwva­ lentes a tener únicamente el caso de p= 1, es decír, el caso para los polinomios

a 0 ( Z 1> Z:u · ·· Z,k ) y a 1 (Z1 ·l-i ····Zi,) ¡Jx, y) las relaciones no lineales Recuerde que·

<l>"( x, y ) = };a¡(z1 .z2 •••• •z,,,)

C(q-') "" A(q-1)S(q-1) + q-d R(q -' )

( E c 59)

donde:

Si se sustituye en (Ec. 53)

(Ec. 54)

(Ec . 55)

(E c 56)

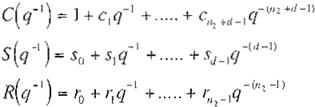
( E c. 60)

;

Con esta identidad polinomial se pueden

)

calcular los valores de S(q·1

y R(q·1

para un

entonces la ecuación quedaría como:

A ( q- 1 )y = q-r1 B( q- 1 )x k + cl>k ( x,y )

valor determinado de C(q·1 .

)

Si se calcula

con

( Ec . 57 )

A( q- 1 ) = l+ a¡q-1 + ....+ ª"iq-""

B( q-1) "" bo + h1q-1 +.... + b,,'q -" i

( Ec . 5 8 )

C{q- ' ).-. = A(q- 1 )s{e(' )y + q· d R(q ')

e(q-').v - s( q-• )A(q-1 ).v + q-•R(rt" ')

C( q-' }y = S( q-• )(q-"{ BA +<I>( r .y)}]+ q-.iR( q-1 )

c(q-1)y -q-[s(<f 'X e(q-1)x +<1>(x.yJ} + R( q·')y = q...,_v

1

donde los parámetros a, y b

son desconocidos

(Ec . 61)

y serán obtenidos utilizando la teoría descrita.

Observe que estos parámetros son los pesos de la RNAP.

Considérese que se cumplen las siguientes suposiciones.

A.1) n1 y n2 son fijos y el retardo d es conocido A.2) q-d B(q- 1 ) tiene todos sus ceros den­ tro delcírculo unitario y bo*O

Considérese también que se cumple la si­ guiente relación·

Re v. Centro ln v (M éx) Vol. 4. Num. 15 Agoste 2000

( E c . 62)

Fi g ur a 12 Esquem a de Control Adaptabfe c o n

RNAP

33

se define la acción de control como :

(Ec 63 )

Otr- /

t '

. :

iiCT•

B(q - 1 )X

1

= -<j>( x ,y )

.&

:>. '

2

S(q- 1 )B(,/ ) X

+ R( q- 1) = y°

/

,. I

Si el sistema es estable (fase mínima)

r

o 1 !

entonces !Y.ti < oo lx,1< oo

ne ----··--

1 ..rr1p

r_\¡Jf 1?1(

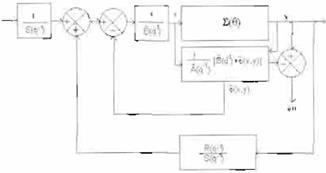
El esquema de control se muestra en la Figu­ ra 12. Los parámetros A(q- 1). B(q-1 ). y ¡Jx,y) pueden ser estimados por RNAP utilizando AG

)

y posteriormente es posible ajustar la dinámica colocando los polos con C(q·1 . Los siguientes ejemplos muestran la aplicación del algoritmo para el caso lineal y no lineal. Todos los progra­ mas utilizados en la simulación fueron desarrolla­ dos en Matlab

E1emplo 1 Caso Lineal

G( z) = Y( z)

Figura 13 Respuetd a l Escalón par a S 1.stem¿;

Lmeal

El procedimiento para aplicar u control adap­ table con RNAP es el siguiente:

1. Identificación de la planta utilizando una señal aleatoria u(k) con distribución uniforme U(-1, 1) . os parámetros utilizados para la red son p= 2, n1 =n2=2. Pm=0.2. nP=3 , n1=3. Para este ejemplo este paso es equivalente a obtener el modelo simplificado utilizando herramientas tradicionales del área de identi­

Considérese que

U (z) es la función

ficación y control.

de transferencia de un sistema lineal donde:

2

-Y( z) 4.9834e - 3 + 3.3002e - 5: ··- 4.9174,, -3z-

2. Probar los resultados utilizando otra entrada como r=sen(t).

3. Separar las partes lineal y no lineal del

1 1

U(z)

1- l .980 l z-' + 9.802e - 1¡,·l

(Ec. 64)

modelo para obtener A(q- ), B(q- ) y 11>k(x,y)

respectivamente para cancelar la dinámica no lineal y adaptar la dinámica lineal del sis­ tema. Como se puede observar en este caso

La respuesta al escalón se muestra en la Figura 13. En este caso se puede observar que el tiempo de establecimiento del sistema ts =5 seg. El período de muestreo es T=0.01 seg.

34

o ( x .y) = O , es1o significa que no existe parte no lineal y los resultados se obtienen aplicando únicamente un controlador adaptable típico. Escogiendo los siguientes valores para C:

(Ec . 65)

se escogió una dinámica que tenga un tiempo de establecimiento igual a Is= 1 seg.

Rev Centro lnv (Mex) Vol, 4 Num 15 Agosta 21/00

• : . -- ,

Artí c ulo

; :1

..i;,¡ •

1

.)"\ ""' di

o

¡ ·------

lr-7

u·:

A 1

..¡

' ,

f •• t u

l.

/ 1

"

.\

'-·

"

10. .o-: JOO

Fiqura 1 4 Resput::sta con Controlado r

La Figura 14 muestra la respuesta original, la salida deseada y la salida con el controlador Como se puede observar la respuesta al con­ trolador tiene un tiempo de establecimiento de 1 seg., tal y como se definió con el valor de C. De igual forma el error entre la salida deseada y la salida del sistema con el control es muy pequeño.

Ejemplo 2 Ca->O No lineal

2

En este caso se va a utilizar un modelo no lineal matemáticamente muy simple propuesto por May (40). Este modelo tiene la siguiente repre­ sentación:

F igura 15 Serie de Mey

El modelo que se propone como entrada para este sistema es el siguiente:

(E c 67 )

1 U 1

Y /<

= r( I - •VJ.-1 )

(Ec 66)

Con r=1.2 y y0=0.5 se obtiene una dinámica caótica sin el uso de algún tipo de entrada. La serie de tiempo generada por esta ecuación puede observarse en la Figura 15.

R ev . C en tr o /n v . ! Máx ) V ol . 4 , N(lm. 1 5 Ag os to 200 0

Fig ur a 16 Sene Identificada por RNAP

El proceso de identificación se muestra en la Figura 16 utilizando los mismos parámetros para la RNAP que en el ejemplo anterior. La única diferencia es el rango de valores de la señal de entrada u E [-0. 1,O. 1}. Separando la parte lineal de la no lineal en la misma forma que en el ejemplo previo, con el mismo valor para C, se puede observar en la Figura 17 el resultado de la metodología propuesta.

35

Anículo

La gráfica de respuesta al escalón (salida con control) es la misma que el sistema hneal obtenido en el ejemplo anterior con un liempo de establecimiento de 1 segundo.

s" dJ L"•J • 1 r1¡(1·I

r os 1

1

!

neal para ajustar la dinámica de la planta "linea­ lizada". El éxito del control adaptable radica principalmente en que el proceso de identifi­ cación aproxime lo mejor posible la dinámica no lineal de la planta. En este caso se utilizó un esquema de fase mínima pero la aplicación a s;stemas de fase no mínima es similar usando la descripción de la Sección de Control de Sis­ temas Lineales de Fase no mimma en Tiempo Discreto. Por ser un control adaptable indirecto la ley de control utilizada puede ser cualquiera que cumpla con los requerimientos de desem­

300

peño deseado.

1'líl 1]1]

·oa 4QO

IJo'--oo e

DO-·--o'o

10 Etrnr

F íg ura 1 7 Res p uesta c on Control a d o r

Discusión de Resultados

Como se puede observar en los ejemplos ante· riores la RNAP es capaz de generar los parámetros para identificar un sistema no lineal. La combinación de la red neuronal con algorit· mo genético permite extraer la información y las relaciones que existen entre los datos de los patrones de entrenamiento, optimizando el error y obtenido la estructura óptima de la red. El modelo utilizado de algoritmo genético per· mite asegurar la convergencia del proceso uli·

lizando la mutación y el procedimiento de agre­

gar padres.

Si se utiliza la RNAP para sistemas lineales el resultado es un modelo simplificado utilizan­ do únicamente los elementos del modelo. Esto es equivalente a obtener la versión óplima del modelo ARMAX .

La naturaleza de la RNAP permite que hacer una separación de la parte línea! y no lineal del sistema o planta. La parte no lineal identificada se utiliza para cancelarla del sistema dinámico original y se aplica un controlador adaptable li·

3 6

REFERENCIAS

(1) Anlsaklfs, P J , lntelligent Learníng Control, Control Systems. vol. 15, núm. 3,Junio 1995.

(2) Cox. E.. Fuzzy Fundamentals, IEEE Spec­ trum. USA, octubre, 1992.

(3) Gupta, M. & Rao D., Neuro-Control Systems. A Tulonal. Neuro-Control Systems, Theory and Applicalions. IEEE Press.1994

(4) Landau, l. D.. R. ozano & M. Saad, Adapt1ve Control. Springer Verfag, 1998.

(5) Levin. A. & S. Narendra, Control of Nonlinear Dynamical Systems Using Neural Networks: Controlabilily and Stabilizatíon. IEEE Transac­ t10ns on Neural Networks vol. 4 , núm. 2, marzo 1991

(6) Phan, D. & S Oh . Adaptive Control of Dyna­ mic Systems using Neural Networks. Pro­ ceedmgs of IEEE lntematíonal Conference on System Man and Cybe me(Jcs, 1993.

(7) Funahashi, K , On the Approximate Realiza­ tion of Continuous Mappings by Neural Net­ works Neural Networks . vol. 2, pp. 283-192, 1989.

(8) Hornik, K.,M. Stinchcombe & H. White. Mul­ tilayer Feedfoiward Networks Are Universal Approximalors. Neural Networks. vol. 2, pp. 359-366. 1989.

(9) Cybenko, G., Approximationn by Superposi­ tions of Sigmo1dal Function. Mathemalícs of Control Signal s and System vol. 2, pp 303- 314, 1989.

(10) Cotter. N , The Stone-Weierstrass Theorem and lts Appl1cat1on to Neural Networks. IEEE Transactíons on Neural Networks vol. 1, núm. 4, pp. 290-295 , diciembre 1990.

{11) Girosi, F. & T. Pogg10, Networks and the Best Approximation Property. Biotog1caf Cyberne­ fics, 1990.