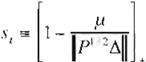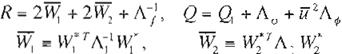Control adaptable indirecto
usando Redes
Neuronales
Dinámicas
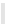 M
A.
Moreno-Armendariz
1
,
W. Yu-Litt
& A S Poznyak z
M
A.
Moreno-Armendariz
1
,
W. Yu-Litt
& A S Poznyak z
1
Escuela de Ingeniena ULSA.
< mmoreno@ci.ulsa .mx>
2
CINVESTAV-IPN
,
Sección d
e Control Automático.
<{yuw.apoznyak} @ctrf.cinvestav mx>
RESUMEN
En estelrabaJo se propone un nuevo tipo de control no-lineal por retroalimentación para una clase de sis temas continuos no-lineales de una entrada y
una sahda de la siguiente forma : Se supone que el sistema no-lineal es desconocido, así una red neuronal dinámica multicapa es usada para
identificarlo Usando un análisis tipo Lyapunov, una nueva ley de actualización estable es presentada , además la estabilidad global es probada .
Finalmente. se presenta la aplicación de dicha técnica al sistema no-lineal TORA mediante simulaciones.
Palabra
s
clave
: Con
trol
por
Retro
alimentación,
Ley
de
Apre
ndizaje,
Redes Neuron
a
l
es
Dinámicas
.
ABSTRACT
In this work, we modify the nonlinear feedback control in following direction: we assume that the nonlinear system is unknown , so the dynamic
multilayer neural networks are used. By means of a Lyapunov-like analysis. a new stable leaming law is proposed. The global stability of dynamic is
presented. Finally the boundness of output tracking error is proposed. We illustrate the applicability of these results by a nonlinear benchmark
problem: rotalional-translational actuator.
K
e
y
words: Feedb
ac
k
Co
ntrol,
Learnín
g
l
a
w,
Dynamíc
Neur
al
N
et
works.
1 INTRODVCClÓN
Indudablemente, desde que ha habido un fuerte renacimiento en la ultima década, las redes neuronales artificiales (RNA) están jugando cada vez un papel
mas importante en la Inge niería. Por algunos años, éstas han sido una considerable promesa para aplicaciones en control no-lineal. Esta promesa esta
basada en su capacidad teórica de aproximar arbitraria mente bien mapeos continuos no-lineales.
En su mayor extensión, la aplicación de las redes neuronales al control automático es usualmente para aproximar el modelo de la planta y, con base en
este modelo, diseñar la ley de control. La pnncipal estructura de las
redes neuronales en uso es la red neuronal
estática (RNE): el procesamiento de la informa ción entrada - salida , por la red neuronal, da como resultado un mapeo algebraico no-lineal.
Con base en la capacidad de las RNE para aproximar cualquier función continua no-lineal, una extensión natural es aproximar el compor tamiento
entrada-salida de los sistemas no-lin eales usando redes neuronales dinámicas (RND): su proceso de la información está descrito por ecuaciones
diferenciales en tiempo continuo o por ecuaciones en diferencias en tiempo discreto. Existen resultados en este tipo de redes. pero requieren de
condiciones muy restr ictivas como estabilidad en lazo abierto o
que el tiempo pertenezca a un conjunto cerrado.
Rev Centro lnv (M&x) Vol 4 Núm 16. En&-Jun. 2001
13
 _i\
l'IÍCU /o
_i\
l'IÍCU /o
Este trabajo busca familiarizar al lector con el nuevo campo de las redes neuronales dinámi cas aplicadas al control no-lineal. Por lo cual.se
presenta un análisis sistemático para la identifi cación, estimación de estados, y seguimiento de trayectorias para sistemas no-lineales. La
herramienta principal para el análisis es el enfoque de Lyapunov.
1 ·1 El problema de identif1cac1on y cont ol
En este trabajo se plantea como objetivo gener al, proponer una herramienta que ayude en el campo de la identificación y en el caso del con trol para
una clase de sistemas no-lineales, como lo es el sistema no-lineal conocido como: Oscilador Traslacíonal con Actuador Rotacional (TORA) para el cual se
propone un control adaptable directo e indirecto. Se asume que el sistema es de la forma:
,\·I "' X 2
X2
= X 3
. ,, = /(x) + g( x)u y = x,
(Ec.
1)
Las funciones f y g son desconocidas. por lo cual se propone una RND para identificar el sis tema y diseñar una ley de control: u Effi .
1.2 Mot1vac1on del trabajo
Debido a la complejidad y variedad de sistemas no-lineales, en este trabajo se propone utilizar las redes neuronales dinámicas para resolver el
problema de identificación y de control para la clase de sistemas no-lineales (Ec. 1}. Dado que éstas han demostrado su gran capacidad como
aproximadores (1), resultan ser una herramienta adecuada para la solución de estos problemas.
1.3 Estructura del trabajo
La estructura del trabajo consiste en dos partes principales:
1. El identíficador : Una RNO es usada para reconstruir el modelo de la planta ; así, la RND
14
se utiliza como identificador. Dado un sistema no-lineal, se tiene acceso a la medíción de la salida del sistema; así la RND se usa para iden tificar
al sistema.
2. El controlador: Una RND es usada para diseñar una ley de control que resuelva el pro blema de seguimiento de una trayectoria dada Así, dado un
sistema no-lineal, se usa una RND para identificar al sístema y con base al resulta do de esta identificación se diseña el neuro con trolador.
2 REDES NEURONALES
2.1 Introducción
La última meta de la ingeniería en control es implementar sistemas automáticos que pudier an operar con un mayor grado de independen cia de las
acciones del humano en un ambiente no estructurado y con incertidumbres (2). Tal sistema puede ser nombrado como autónomo o inteligente.
Pudiera necesitar sólo ser presenta do como una meta y podría alcanzarse este objetivo con una iteracción continua con el ambiente a través de una
relroalimentación acerca de su comportamiento. Podría continuar adaptándose y ejecutando tareas con una gran eficiencia en condiciones impredecibles y
cam biantes. Esto sería muy úhl cuando la iteracc16n directa del humano pudiera ser peligrosa. propensa a faltas, o imposible.
Los sistemas biológicos son posibles esqueletos para el diseño de tales sistemas autónomos. Ellos proveen muchas pistas para el desarollo de
aprendizaje robusto (altamente estable) y algoritmos adaptables. Los sistemas biológicos procesan la información, de forma diferente a los esquemas de
control conven cionales; éstos no se basan en ningún modelo y son muy eficientes para tratar con íncertidum· bres y complejidad. No requiren del
desarrollo de un modelo matemático para ejecutar tareas complejas. Ciertamente, pueden aprender a ejecutar nuevas tareas y adaptarse fácilmente a
cambios en el ambiente. Si los principios funda mentales de la computación encajaron en los sistemas nerviosos, es comprensible que una generación
totalmente nueva de métodos de control pudieran ser desarollados mas allá de las capacidades de las presentes técnicas basadas en un modelo matemático
explícito.
Rev
Centro lnv. (Mex) Vol 4, Núm
16, EM-Jwr
2001
-
Ani culo

Un sistema de control tiene la habilidad de aprender, si adquiere información durante la operación, acerca de comportamientos desco nocidos de la
planta y su ambiente, de manera que la ejecución completa es mejorada. Con este enriquecimiento del controlador con el aprendizaje, es posible expander
la región de operación y finalmente la implementación de sistemas autónomos.
Una clase de modelos, que tiene la potencia lidad de implementar este aprendizaje, son las redes neuronales artificiales. Ciertamente, la morfología
neuronal del sistema nervioso es mucho más compleja. No obstante, una analogía simplificada puede ser desarollada. la cual podría ser utilizada en
aplicaciones de ingeniería. Basándose en esta comprensión simplificada , las estructuras de las redes neuro nales artificiales pueden ser
desarrolladas.
2.2 Modelo de una neuronal
Una red neuronal artificial (RNA) (3) es un ele mento capaz de procesar gran cantidad de información de forma paralela y distribuida, inspirada de las
redes neuronales biológicas (ver Fig.1), las cuales pueden almanecenar conocimiento exprimental y tenerlo disponible para su uso (4). Esta tiene
algunas algunas similaridades con elcerebro, como lo son:
1 El conocimiento es adquirido a través del proceso de aprendizaje.
2. La conectividad entre neuronas es llamada pesos smápticos y son utilizados para almace nar el conocimiento.
Figura
1
Esquema de una neurona biológica
.
Rev
Centro /nv (Mex) Vol 4 Ntím
f6
.
Ene-Jun 2001
El procedimiento para el proceso de aprendi zaje es conocido como el algoritmo de apren dizaje. Su función es modificar los pesos sináp ticos de las
redes para alcanzar una meta preestablecida. La modificación de los pesos provee el método tradicional para el diseño e implementación de las redes
neuronales.
WkJ f'unc1on dc
xl acti1r,>CJon
\Vl:2 0 ·lk i<
Señales 1'l • • .... ti( ) "fa
de en(r.)oa l':_/
¡ W}:p 1
'11 • Umbral
Pescis
S111C'!'IJCOS
Figure 2 Modelo no-lineal
de
una
neurona
La neurona es la unidad fundamental para la operación de la red neuronal. La Fig. 2 muestra el esquema de una neurona.
Existen 3 elementos basicos de la RNA:
1. Un conjunto de uniones de sinápsis, con cada elemento caracte rizado por su propio peso.
2. Un sumador que suma los componentes de la señal de entrada, multiplicados por su respectivo peso sináptico.
3. Una función de activación no-lineal que transforma la salida del sumador en la entrada de la siguiente neurona.
Un umbral externo es también aplicado para reducir la entrada a la función de activación. En términos matemáticos. la í-és íma neurona puede ser descrita como:
n
u, =
¿
w
& x
j
j -J
y¡
= a( u, - p,)
(Ec
.
2)
1
5
 '
1
l_dít.u/j
J
• -·._· l:
'
1
l_dít.u/j
J
• -·._· l:
donde:
x, j-ésimo
componente de la entrada.
w
,
j
peso de la conexión entre la}·ésima componente de la entrada y la i-ésima
neurona.
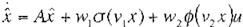 Tiempo continuo:
Tiempo continuo:
(
Ec
.
.:J)
p,
a(.)
salida del sumador. umbral.
función de activación no-lineal.
donde a(.) y <P(.) son funciones sigmoidales.
--•,_A_- -
Y
,
salida de lai-ésima neurona.
r MLP
 La función de activación no-lineal, es denota da por g(.) y genera el elemento de la salida y, ,
La función de activación no-lineal, es denota da por g(.) y genera el elemento de la salida y, ,
recibiendo como entrada x; :
->/.'-..- ......
"? ...........r ,,
Y
,
= g( x, )
2.3 Estructura de las redes neuronales
(Ec. 3)
'------------·-·· ··---
Fi
g
ura
3 Esquema
1
e
una reJ
nevror1al
<
ímám1ca
Los ciclos de retroalimentación (ver Figura 3} resultan en un comportamiento dinámico no lineal debido a la función de activación no-lineal de las
neuronas. De ahí que el término de las
La forma como las neuronas de una red neu
ronal están interconectadas determina su estructura . Para propósitos de identificación y control. las estructuras más usadas son:
1. Redes de alimentación hacia adelante de una capa.
2. Redes de alimentación hacia delante mullicapa.
3. Redes de funciones radiales básicas
4. . Redes neuronales dinámicas.
2.3.1 Redes neuronales dinam1cas
Este tipo de redes se distinguen de las redes neuronales estáticas en que éstas tienen al menos un ciclo de retroalimentación. Estos ci clos
involucran el uso del tiempo discreto, y de bifurcaciones compuestas por elementos de una unidad de retraso. Esta unidad se denota por q·1 , tal que 11(k - J ) = q·1 u(k) , con k indicando el k-ésimo muestreo en el tiempo. La
ecuación de las redes neuronales dinámicas seria:
Tiempo discreto:
y( k),J\
k
+ 1),- ·-,y( k - n),
y(k + l) - [
redes neuronales dinámicas (RNO) describe mejor este tipo de estructura de las redes neu ronales. Debido a estos hechos, las llamaremos redes
neuronales dinámicas.
Estas pueden ofrecer grandes ventajas computacionales. De hecho, es bien sabido que un sumador lineal estático finito es equivalente a un sistema
lineal retroalimentado de un solo polo, como se ve en la Figura 4.
 ..
..
-
"'/ _,

:. L /
g_/
Figura 4
Sistema
dinámico
y
estático
eowvafente
De la Figura 4, el sumador de salida de el sis tema dinámico es:
v(k)
= u( k) + u(k + 1) + ···+ u( k - n)
= " u(k - i), n _.,. oo
_ , - , u( k),u( k + I),··-,u(k - m)
(E
c
.
4)
1-0
(Ec.
6)
16
Rev. Cenrro
1
1w.
(M
xi
Vol 4
,
Num 16 E11e-Jun. 2001
El sistema lineal descrito por:
v(k
)
= v( k - 1) + u( k )
cluya las perturbaciones , ver (8). Casos espe ciales de este modelo son considerados en (9).
Una aproximación obvia del modelo del sis
v(k) 1
-1 _,., _,.
tema es seleccionar la estruc1ura de
u(k )
- l- q-1 = 1 + e¡ + q - + . . . + q
v (k) = u( k ) + u( k
-
1
)
+ ···+ u( k - n)
{Ec;;
7)
Es claro que las dos estructuras son equiva lentes, pero desde el punto de vista computa cional, el sistema con retroalimentación es equivalente a
una muy grande, posiblemente
infinita, estructura estática. Esta propiedad es muy interesante para identificación y control, y abre el camino para las aplicaciones de las redes
neuronales dinámicas en estos campos.
entrada/salida de la red neuronal para que sea la misma que tiene el sistema . Denotando la salida de la red neuronal como y,,,,, existen dos
posibles estrategias.
2.4.1 Estrategias de Identificación Ex isten 2 tipos de modelos:
a) Modelo serie paralelo: En este caso, las salidas del sistema y son usadas como entradas de la red neuronal. este modelo esta desCíito por la (Ec.
9).
2 4 Redes Neuronales en ldent1ficc··
Las redes neuronales tienen el potencial de ser
(/,·+ l - () ¡
y( k),y(k
+ l),- ·-,y( k - n),l
aplicadas para modelar sistemas no-lineales. Una pregunta importante es si el sisteMa es identificable (5), i.e. si puede ser el sistema dinámico en
consideración, adecuadamente representado sin ser necesario dar un modelo estructurado particular. La ldentificabilidad en redes neuronales está
relacionada a la unicidad de los pesos y si dos redes con diferentes parámetros pueden producir un comportamien to idéntico entrada/salida.
Resultados en este tema se encuentran en (6) para redes neu ronales estáticas. y en (7) para las dinámicas.
Para representar los sistemas no-lineales con redes neuronales, una aproximación cor recta es incrementar las entradas de la redes con señales
correspondientes a sus entradas y salidas. Asumiendo que el sistema no-lineal está descrito por. ver (3):
v(k + l) = r(k), \'(k + l).···, v( k - n),
- ' •
• ' [u( k),u(k + l),- ·-,u( k - m)
y,u
EITT, m s. n
( /_
[
1
Este modelo no considera las perturbaciones directamentamente. Para un método que in-
Rev Centm
lriv (Mt?x}
Vol 4 Núm f 6. ne-Ju .. 2001
Y,.,, '
) - <'> u(k ),u( k + l ), ...,u(k - m)
(Ec. 9
)
Dado que no existe recursividad en la ecuación, ésta corresponde a una red neuronal estática como la que se muestra en la Figura 5.
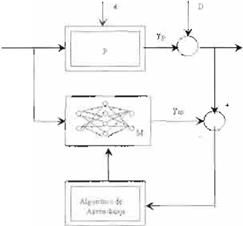
Figura 5 Esq1Jema
de
iden!i'"1cación
de
una red
esrá;,ca
b) Modelo paralelo: En este modelo las sali das pasadas de la red neuronal son usadas como componentes de la entrada de la red,
este modelo está descrito por
17
!\ nfculo
- - • _.: ..,

= [Y"',(
k ),y "n(k + 1),..·,
Y1111 ( k - n),l
1
)
"" u(k ), u( k + 1),.··, u(k - m)
(
E
c.
10)
Dado que existe una recursividad de y,.,, en la (Ec. 1O}. esta corresponde a una red neuronal dinámica.
Observación 1: La regla de actualización de pesos de fa estructura serie paralelo (10), (11)y la estructura paralelo son muy similares. la única diferencia es que fa serie paralelo obtiene a la matriz de ganancia P de fa solución de la siguiente ecuación de Lyapunov:
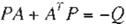
(
Ec.
1
1
)
En el caso
de Ja estructura
paralela
obtiene Ja
matriz de ganancia
P de la solución
de Ja
ecuación
de Ricatti.
2 4 2 Aproximación del Perceptrón Dinámico Multicapa
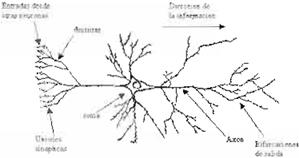
Considere el siguiente perceptrón dinámico multicapa (PDM) en tiempo continuo:
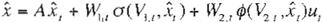
(Ec
12)
donde Vt E[O,oo) :
x,
EUf' es el vector de estados de la red neuronal.
Effik es el vector de entradas
1
A
Emk es una matriz estable, que puede ser seleccionada .
1 .1 "1 , v u1 son o pesos
|
|
W
Ero" -'"'
W E00 "_.,. 1 de
las capas ocultas de la red neuronal.
a
(
.)
E "' es un vector de funciones sig moidales.
<1>(.)
Effi"'xm es matriz diagonal, i.e.,
1
8
<P(.)
= dia </>1 < Vz., x,),···,</>mO;;,, x,) ]
Si k < n·1 ,entonces u; ::: O para i = k + l , ···, m .
Las funciones sigmoidales usadas ena(.) y <f>( .)
cumplen con la (Ec. 12)
a,
0
¡
.X;
= l + e·b,x , -C¡
(Ec
· ¡
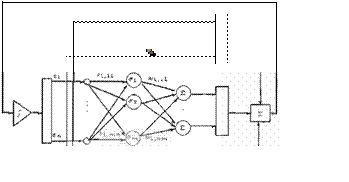
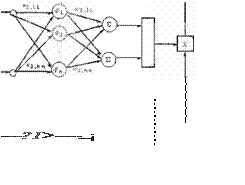
La estructura del perceptrón dinámico se mues tra en la Figura 6.

 .,-
.,-
Figura
6 Estruclura generQl de! pert:eptrón
dm/Jm1co
multu::apa
Las redes dinámicas convencionales (RNO) son las redes neuronales que corresponden al caso:
m
= 11 y v; = v2 = {
(é:
r,
.
14)
Usando el PDM de la (Ec. 12) para identificar el sistema no-lineal descrito por
Rev
C
1Jn
rm
/rw
(M.)
VOi
il
Nvm
16 Eroe-,Jun 2{t<J
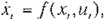 \f
r
E[O, oo)
\f
r
E[O, oo)
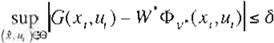 (
Ec
!f)
(
Ec
!f)
_.-:_.---- _
_ :_ · · ·A r1íc11/o 1
 v, = w· := p1·w;1 Y v, = v·:= r v;"' v2• 1 .
v, = w· := p1·w;1 Y v, = v·:= r v;"' v2• 1 .
tal que
e- ro" rorn
f {\)" "' ('(.)'1
donde 1 c:uL 1 EJi ;.H - '-' L es
un campo vectorial suave continuo, definido en un conjunto compacto e EITT"""' .
Se asume que f (x,, u1,l ) satisface la condición de Lipschitz, i.e.,existe una
constante 1> O tal que para todo par de puntos (x1 "ui).(.x:2.I' u) E8 ,
se tiene que:
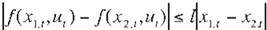
(Fe 16)
Problema 1: El problema de identificación del sistema dinámico consiste en determinar s1 existe un perceptrón dinámico multícapa (PDM) tal que la (Ec. 12) pueda aproximar el compor tamiento entrada-salida del sistema dinámico de la (Ec. 14).
(Ec
.
18
)
donde o es cualquier constante pequeña. Con base en las suposiciones anteriores se obtuvo el siguiente resultado.
Teorema 1 Sea el sistema dinámico (Ec. 14) y
el perceptrón dinámico mullicapa
(Ec. 11). ini-
c
ian
en el
mismo estado Xo = Xo . Para cualquier e > O y un tiempo finito T>O, existe un
entero
m
tal
que el estado del
POM
x,
con pesos [ ·w1·v,= \{] satisface:
sup lx, - .x,¡ < e
O.:t s7
Si se define vV, := [ VY; , W¡, 1
(Ec
.
19)
y La demostración de este teorema puede ser revisada en (12).
<P,; (i"ui) :=[a( 1 xi)( _,x,)T
12) y ( Ec. 14) se rescriben como:
x,
= Ai, + l· <f> 1 (x,,u,)
x
,
= Ax
,
+ G( x,,u)
y las (Ec.
(.:e
17)
2.5 Redes Neuronales en Control
Con una referencia específica en las redes neu ronales en control las siguientes características y propiedades son importantes:
a) Sistemas no-lineales: Las redes neu ronales son una gran promesa en el campo de los problemas del control no-lin
donde:
G(x,, u,) =
f (x
u
)
-
Ax
,
.
eal. Esta proviene de su teórica habilidad para aproximar mapeos no-lineales arbi trarios.
Obsérvese que W,<l>v, ( x,,u,) es una PDM en
tiempo continuo. del teorema de Stone-Weier- strass si la capa oculta (v; , V2,) es lo sufi cientemente grande (m es suficientemente
grande), W.<l>v,( x,,u,) puede aproximarse G(.x:r> u1 ) con cualquier grado de exactitud
para todo (x1 , u, ) E8 . Por ello existe
Rev Centro /11V (Méx) Vol. 4 Ntim. 16, f!niJ·Ju11 ?001
b) Procesamiento Distribuido Paralelo: Las redes neuronales tienen una estructura sumamente paralela que les permiten in mediatamente realizar una
implementa ción paralela. Con tal implementación puede esperarse alcanzar un mayor grado de tolerancia a errores que los esquemas convencionales.
19
Artículo
- - - -- -

c) Implementación en Hardware: Este punto está muy relacionado con el punto anterior. Las redes no sólo pueden ser implemen tadas en paralelo, algunos
vendedores han introducido recientemente implemen taciones utlizando un hardware dedicado VLSI. Este proporciona velocidad adicional e incrementa el
número de redes que pueden ser implementadas.
d) Aprendizaje y Adaptación: Las redes neu
pasados del sistema en estudio. Una red propiamente entrenada tiene la habildad de generalizar cuando se le introducen datos diferentes a los
utilizados para su entrenamiento. Las redes pueden ser además adaptadas en línea.
pueden operar simultáneamente con datos cualitativos y cuantitativos. En este punto las redes se encuentran en algun lugar en medio del campo entre los
sistemas tradi cionales de ingeniería (Datos cuantita tivos) y las técnicas de procesamiento del campo de la inteligencia artificial (datos
simbólicos).
f) Sistemas multivariables: Las redes neu ronales naturalmente procesan muchas entradas y tienen muchas salidas: por lo que ellas pueden facilmente
ser aplicadas para sistemas multivaribles.
Desde el punto de vista de la teoría de con trol, la hab1hdad de las redes neuronales para tratar con los sistemas no-lineales es muy importante. La
gran diversidad de los sistemas no-lineales es la primera razón del por qué una teoría general y sistemática aplicable para el diseño de control
no-lineal no ha sido todavía desarrollada. Sin embargo, existen algunos métodos tradicionales para el análisis y síntesis de controladores no-lineales
para clases específicas de sistemas no-lineales, como lo son: métodos en el plano de fase, técnicas de linealización y funciones descriptivas.
Sin embargo, es la habilidad de las redes neu ronales para representar mapeos no-lineales, y de modelar sistemas no-lineales, la caracteristi ca más
importante para usar a las redes neu ronales en la realización de controladores no-
20
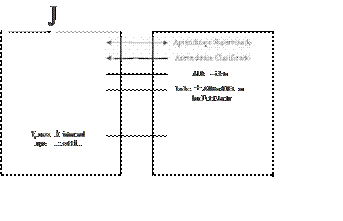
lineales Una vista de las relaciones generales entre los campos de la ciencia del control y las redes neuronales es mostrada en la Figura 7. Los
cuadros blancos son utilizados cuando una similitud obvia no exista.

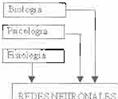





 Figu
r
a
7 Relación entre fas redes neuronales
Figu
r
a
7 Relación entre fas redes neuronales
y
el control
2.5 1Estructuras de C•)ntrol
Una gran cantidad de estructuras de control han sido propuestas. Para una revisión reciente y completa. ver (13) En la literatura de aquitec turas de
redes neuronales aplicadas en el con trol han sido propuestas y usadas una gran can tidad de estructuras de control; aquí se mues tran dos de las
rnás importantes
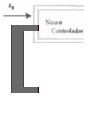
1. Control Directo: En esta estructura (14), el neuro-controlador es entrenado sin tener el modelo de la planta. En este esquema. ver Figura 8 se busca
que el resultado del lazo cerrado que contiene a la planta y al sisterna dé como resultado un mapeo identidaci. La acción de control busca que la
planta siga la señal de referencia
R!i'
C
e
11rr
/nv ¡Méx) Vo! 4 Num
1
6
Ene-,Jun
20
01
 ci---'i. -... 1. )
ci---'i. -... 1. )
Figura
8
Esqucm;; gem.
• JI <Je/ control directo
 2. Control Indirecto: En esta estructura (14), primero un neuro-identif1cador estima el comportam iento de la planta, usando como información
únicamenle la salida del sis tema, luego el neuro-controlador es diseña do con base en el modelo identificado , ver Figura 9. La acción de control
busca que la planta siga la señal de referencia
2. Control Indirecto: En esta estructura (14), primero un neuro-identif1cador estima el comportam iento de la planta, usando como información
únicamenle la salida del sis tema, luego el neuro-controlador es diseña do con base en el modelo identificado , ver Figura 9. La acción de control
busca que la planta siga la señal de referencia
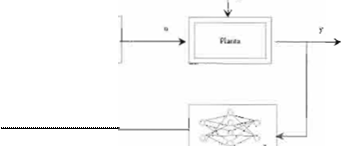

F1g1
.," 9 Es¡¡uema gneml del control indirecto
Observación 2 Note que en la
Figura 8 y en fa Figura 9 sólo se retroalimenta la información de la salida de la planta, esto es dado que se uti lizan RND. por fo cual no se requiere del par entrada/salída , como en el caso de las RNE.
2 5 2 Control Adaptable
Existe una diferencia entre el control adaptable dtrecto e indirecto en el contexo de esta estruc tura. En los métodos indirectos, primero el sis
tema es identificado desde las medidas entra da/salida de la planta y después el controlador es adaptado basándose en el modelo identifica do. En los
métodos directos el controlador es aplicado sin realizar una identificación previa del sistema , por lo que ésta se lleva acabo en línea. Las redes
neuronales pueden ser uti lizadas en ambos métodos .
Parte delcontroladaptable neuronales basa
do en el método Indirecto. En este método,
r?ev.
Centro
1!111
(M6x l
Vol 4 Núrn rr., Ene- Ju;¡ W01
primero,un modelo del sistema es obtenido por la red neuronal en línea utilizando medidas de la planta y entonces una de las estructuras de control
citadas anteriormente es implementada encima de este modelo adaptable neuronal.
Uno de los primeros resultados en redes neu ronales adaptables no-lineales es (9), donde con base en modelos neuronales específicos , el controlador
basado en el modelo adaptativo indirecto es implementado. En (15), un control adaptable IMC es desarrollado usando redes neuronales RNFB. Aplicaciones
para control de robots, donde las RNE son usadas para estimar adaptativamente parte de la dinámica del robot, son presentadas en (16). Basada en un
modelo identificado del sistema en linea por una RNO , explicada anteriormente , en (10),la ley de con trol es construida para asegurar el seguimiento
del modelo de referencia lineal.
Estimando un control neuronal adaptable directo, en (17), un controlador adaptable es desarrollado usando redes neuronales RBF. En (14), una
combinación de ambos métodos es usada; de hecho, un modelo de una RND es adaptado en linea,también como un neuro-con trolador dinámico.
3 MODELADO DEL SISTEMA NO-LINEAL TORA
3.1 lntroducc16n
El sistema mostrado en la Figura 1O representa un oscilador lraslacional con actuador rota cional (TORA) (18). Fue introducido por primera vez. en (
19), siendo utilizado como un sistema no-linealestándar en un número reciente de tra bajos (18), (19) con el propósito de realizar pruebas de
comparación entre diferentes meto dologías de oontrol.
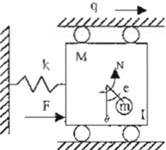
Figvra 10 Osc;tlador Traslac;ional con
Actuador
Rotacional
(TORA)
21
Artículo
- - - - 1

3 2 Modelo Lagrang1ano
El oscilador consiste en una carro de masa M conectado con una pared fija por un resorte line al con una constante de rigidez. k. El carro
está lfmitado a una dimensión de movimiento. El actuador que está unido al carro tiene una masa
m
y un momento de inercia l desde su centro de
masa, que está localizado a una distancia e desde el punto en el cual la masa rota. El movimiento ocurre en el plano horizontal , por lo que la fuerza
gravitacional no requiere ser con
siderada (ver Figura 1O), donde N denota el control del torque aplicado a la masa m, y F es una fuerza de perturbación sobre el carro.
donde s es la posición normalizada de la posi ción del carro, w y u representan una pertur bación adimensional, el control
del torque. respectivamente. En las ecuaciones normal izadas, el símbolo (.) representa la diferen-
ciación con respecto altiempo normalizado .
La unión entre el movimiento traslaciona l y el rotacional esta representado por el parámetro e, el cuál es definido por (un valor
típico e =0.1).
me
E
=--;:::======
+ me
2
)( M
+ m)
(Ec
.
23)
Sea q y q la posición traslacional y la velocidad del carro. y sea ft y e la posición angular y la velocidad
angular de la masa m, donde
e
= Oº es perpendicular al movimiento del carro, y e = 90º está alineado con la dirección
positiva de q . Las ecuaciones del movimiento están dadas por:
( M + m)q + kq = - meces e - 62 sin 8) + F
3 4 Modelo de Primer Orden
Tomando
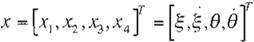 las ecuaciones adimensionales del movimiento de primer orden estarían dadas por:
las ecuaciones adimensionales del movimiento de primer orden estarían dadas por:
x
= /(.x) + g( x ) u + d( x ) w
(/ + me2 )é = -meqcose + N
3.3 Modelo Normalizado
(Ec 20)
donde
Xi
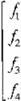


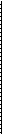
.2 .
-X + E X S
(Ec
24)
Usando las normalizaciones {Wan}:
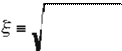 M + m
M + m
/(x) =
1- e2 cos2 -s
X4
ecosx
3
(
x
1
- ex;sin x3)
1- e2 cos2 x,
i
,
-
+
-
m
_
e
_
2
q
?; e --¡;;¡;-;;;
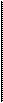


o
-ECOS
u
=
M +
m
N
k(l
+ me2 )
1
 w e-
w e-
k
M +
m_,
F
I
+ m
e
·
l-écos2
g( x) -
o
1
x
3
g ,
o
(
Ec 21)
Las ecuaciones de movimiento se convierten en:
1- E- COS X 3 82
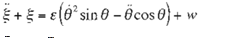 e
= -E z; cose + u
e
= -E z; cose + u
(
Ec
.
22)
d( x)
=
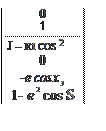 ft::
r;
.
25)
ft::
r;
.
25)
22
Re1 Centro lr111 (MéY) Vol 4. Ntin• 16 Ene-Jun 2001
 ,ro ----- -, · A rt ícuIo
,ro ----- -, · A rt ícuIo
3 5 Modelo eri Casc-ada
El sistema se rescribe de la siguiente forma:
t
,
= <:z
.
E cosz., ( 2 .
F)
Z'2 = 2 2 3 - é(1 ¡;4 ) Slll .;:1 -
1 -
E cos ?;
l
mación local contenida en la estructura de los datos que se le presentan, por otra parte, la fun ción de aproximación es sensible a los datos
utilizados para su entrenamiento (4). Las RND pueden superar exitosamente esta desventaja dado que su estructura incorpora una retroali mentación (22)
(1O) (23).
4 2 RND de una capa para Identificación de Sis temas No-lineales
+ 1 -
E 2 cos?- <:
u
;,.J = Z.:i
4 .2.1Estructur a de la RND de una capa
Z
4
= - + e cosz1 + F
(Ec. 26)
El sistema no-lineal a ser identificado es de la forma:
Más detalles de la obtención de este modelo pueden ser revisados en { 12). Para el resto del trabajo, ver ( 12). se asume que no existen per
x
,
= J ( x,,u,,t),
x
.
,
ron Ero'"
E;11 ,
(Ec
.
2
7
)
turbaciones, i.e. F == O .
Observación 3 El modelo Lagrangíano, Normal izado y el de primer orden son utilízados para la identificación de este sistema usando RNO. El modelo en cascada se obtuvo para implementar una acción de conlro/ usando este modelo vía redes neuronales dinámicas.
4 IDENTIFICACIÓN DE SISTEMAS NO-LIN
EALE
4 1 Introducción
La identificación es uno de los puntos esen ciales en la teoría de control cuando no se cuen ta con la información completa del sistema. Una solución
efectiva es utilizar RNA, pues han mostrado ser una herramienta muy útil para identificar sistemas no-lineales complejos (1), aún cuando la planta es
considerada como una "caja negra''. Los neuro-identificadores pueden ser clasificados como estáticos y dinámicos (9). La mayoría de las publicaciones
que presentan la identificación de sistemas no-lineales usan RNE, como por ejemplo el perceptrón multica pa, el cual es implementado para ta aproxi
mación de funciones no-lineales que se encuen tran en el lado derecho de la ecuación que rep resenta la dinámica del modelo (21}.
La principal desventaja de tas RNE es que la regla de actualización de los pesos utiliza infor-
P.e\I
".:2n/ro Jn, (Mex) Vol 4, Num 16 Erie-J1m 2001
Diferentes redes neuronales se proponen en
{Rovithakis1 , Rovithakis2 . Kosmatopoulos1. Poznyak},en esta sección se analizará la sigu
iente red neuronal de una capa {Yu}:
i, = AX , + l4;,, a(x, ) + l _,1P(X.,)u,
(
Ec
28)
donde:
,r, Effi" son los estados de la RND.
u,
Eüf' es el control dado.
ro,, .rn
W E'°".rn
1 .1 "1 , 2 , " son las matrices
de pesos.
A
Effi"x" es una matriz estable.
a(.) Eül'" es un vector de funciones sig moidales.
q'>(.) E m.•rnn es matriz diagonal, í.e.,
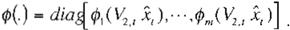
Las funciones sigmoidales usadas cumplen
a(.)
y</J(
.)
con la (Ec. 12)
23
 1
Ad(
ó
ulQ.
·
- -- - -, - · · - =-::-1
1
Ad(
ó
ulQ.
·
- -- - -, - · · - =-::-1

4.2.2 Preliminares
Considérense las siguientes suposiciones:
¡\
º
Y
¡\4>
son matrices definidas positivas.
Se conoce (24} que si la matriz A es estable, el
Suposición 1: El control u, es seleccionado
par
(A, Rl·'2)
es controlable, el par
(Q¡'.2 ,A)
como
ac
otado,
entonce
s:
u
1
,s; ü
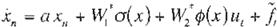 En el caso general. cuando la RND (Ec. 27) no puede identificar exactamente el sistema no lineal dado (Ec. 27) este sistema puede ser re presentado
como:
En el caso general. cuando la RND (Ec. 27) no puede identificar exactamente el sistema no lineal dado (Ec. 27) este sistema puede ser re presentado
como:
es observable, y / a condición especial local de fr ecuencia o su matriz equivalente:
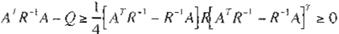
(
Ec.
30)
se cumple, entonces. la matriz de Riccati:
donde:
.
fi
es el error de modelado.
w.·
,
W2* son matrices constantes.
(
Ec
.
29)
(Ec.
31
)
tiene una solución positiva. Siguiendo este hecho,se introduce adicionalmente la siguiente
Dado que las funciones sigmoidales CJ y </> son
uniformemente acotadas. es razonable asumir
que las dinámicas no-modeladas .!, . satis facen la siguiente suposición:
Suposición 2 : Existe una constante positiva '11 tal que:
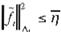
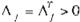
Definición 1: Sea el error de identificación:
fj,,1 = x - x
Suposición 3: Las funciones sigmoidales, comúnmente usadas en las RNO satisfacen la condición de Lipschitz (12):
0
1
1 0
1
s; b./\.,/!!.,,
(
,
u
,
Y
A 2 (1uJ s ¡2!!. l\ b.1
donde:
suposición.
Suposición 4: Para una matriz estable A dada, existe una matriz estrictamente positiva 01 tal que la ecuación de la matriz de Ricatti (Ec. 3í} con:
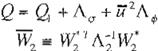
R
=
2VY¡ + 2W2 +
¡ -1
,
= w·r /\-1
1 - 1 1 ) ,
tiene
una
solución
pos
itiva.
E
stas
condiciones
se
cumplen
f
áci
lmente
sí
se
se
l
ec
cion
a
A com
o
una
matriz di
ago
nal estable
.
4.2.3 Regla de Actuahzac 1ón de Pesos
La regla dinámica de actualización de los pesos esta dada por:
.• = -s1[k1P,a( x1{ ]
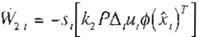
a,
=
a( x
) -
a(x,)
s
;;; </>( X 1) - <P(XI )
donde:
1
E
c.
3
2)
-
ur•
W
1.1
a YY¡ - l,1
24
w
2.t
5 w.;- w2.I
k
,
EITT' ( i = J.,2) son las ganancias de la actu alización de los pesos de la RND.
Re1' C"'ntro lnv. (Mf!x) V1;i 4., Nl1m. 16. Ene-Jr;n 2001
P
es la solución de la ecuación de Riccati dada por (Ec. 31).
rl 1 'l
'\1 .O = ·' W2.0 ::: w;son las condiciones ini
H< o ::: W2 0 :; . L li
ciales.
S,
es la función de zona muerta definida como:
l1 tJ
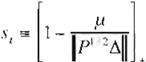
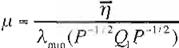 4 .3 Anal!s1s de Estabilidad
4 .3 Anal!s1s de Estabilidad
[:L = {
:: ;::-. o
.: < o
(Ec
.
3
3)
estos valores se utilizarán para identificar al sis tema .
La simulaciones se llevaron a cabo usando el paquete matlab®. Los resultados obtenidos de identificación de los 4 estados se muestran en las Figuras
11-14.
6--------- ---
Teorema 2: Se considera al sistema no-lineal (Ec. 27) y la RND de una capa (Ec. 28) . Si se cumplen las suposiciones 1-4 y los pesos de la RNO se ajustan de acuerdo a (Ec. 32) . Los siguientes hechos se cumplen:
ó1 , H ,,W2 1 EL"'
5 ('' ) (\
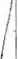

:
! I ¡ \
I
J
I
i
X¡
\
o--- -'-''---- -_,_.__ ,
í.e. el error de identificación y /os pesos de la RND están acotados, además el error de identi ficación satisface el siguiente desempeño de seguimiento:
. l
r r -
limsup - t:.,Q t::,.,s,dt s; r¡
r-"" T Jo
La demostración de este teorema puede ser revisada en (12).
4.31 S1mulac10 s
Problema 2: Identificar los 4 estados del sis
o 5 10 15
Figura 11 Identificación del
estado
usand0 la
RND de una capa
3
2 /
J
I
o
 . \
. \
tema
no-lineal
TORA
(Ec. 26) ,
usando una -2
X
RND
de
una capa
(Ec. 28). l
Solución 1: Se usa la RNO de una capa (Ec.
28) , junto con la regla de actualización de pesos (Ec. 32) con:
Las condiciones iniciales para las matrices de
los pesos son:
Re·•.
C<!nlro
ftw. (MexJ
liol 4. Num lt), Ene Jun. 2001
-3o 5 10 15
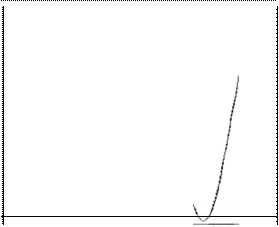
Figura
12
/dent1f 1cac1on
del estado
usando
l
a
RND de una capa
25
·
Art íc ulf>
_ _ _ _
_ _
_ -

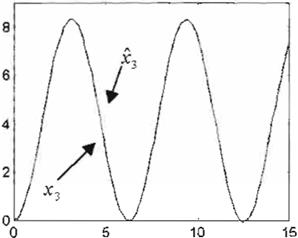
Figura 13 /dent1ficac 1on del estado usarJdo la RND de una cspa
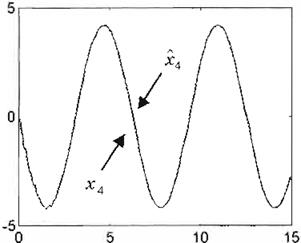
Figura 14 Identificación del
estado usando
la
RND
de una capa
Observación 4 Como se nota en las Figuras 11-14 los 4 estados x del sistema no-lineal son correctamente identificados por la RNO, cuyos
estados son
x
.
5 CONTROL ADAPTABLE INDIRECTO USAN
DO RND.
5.1 Introducción
En el control neuronal indirecto, el contro lador se basa en la identificación del sistema no-lineal, por lo que el proceso de identificación se
convierte en la parte central de la construcción del neuro-controlador. En esta dirección existen 2 tipos de estructuras: El modelo serie-paralelo y el modelo paralelo (9). El modelo serie-parale lo puede asegurar que todas las señales están acotadas. si la planta es BISO estable como se
muestra en (9) para las redes neuronales multi capa de propagación hacia adelante y en (10)
(22) para las RND. Muchos trabajos publicados utilizan este modelo, aprovechando este resul tado de estabilidad .
Por otra parte, el modelo paralelo es muy útil cuando se trabaja con sistemas con ruido. dado que este modelo elimina los problemas del bias causados,
por el ruido generado por la salida del sistema real(25); además, dado que la iden tificación de un modelo usualmente se realiza fuera de línea, el
modelo paralelo es mas ade cuado. Sin embargo, este modelo carece de verificación teórica, por lo cual, se requiere cubrir esta carencia para poder
disfrutar de sus ventajas.
No existen muchos análisis de estabilidad en el campo del control neuronal, por lo que exis ten pocos resultados publicados que se refieran al
análisis de sistemas no-lineales controlados por RND. En (22), (26} se presentan resultados de una versión particular de las redes neu ronales de alto
orden. En (27), (28) una cota al error de identificación es dado usando un análi sis tipo Lyapunov. Es importante mencionar que la metodología del
análisis de estabilidad presentada a continuación es muy similar a la presentada en (29).
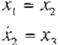 5 2 Planteamiento del Problema La clase de sistemas no-lineales:
5 2 Planteamiento del Problema La clase de sistemas no-lineales:
Las redes neuronales son una herramienta muy efectiva para controlar sistemas no-lineales complejos , cuando no se cuenta con informa ción completa
del modelo o cuando se conside ra a la planta a ser controlada como una·caja negra". Un panorama general del control neu ronal puede ser revisado en
(3).
.X,,
= j ( x ) + g( x)u
.V = Xl
Ec. 34)
 ' - - - - A r iícflfo
' - - - - A r iícflfo
con:
T
x
= [.xi'X2 ,···'x,,] son los estados del sis-
Considérense las siguientes suposiciones:
Suposición 5: El control u, es seleccionado
tema.
f .
S :
·1\"° )\ funciones suaves desconocí-
como acotado, entonces: u1
.s u
-
das con /, (O)=O.
Problema 3 Identificar el sistema (Ec. 34) y diseñar el neuro-controlador que resuelva el problema de seguimiento, usando una RND.
5 3 Estructllra de la RND
En el caso general, cuando la RND (Ec. 35)
no puede identificar exactamente el sistema no lineal dado (Ec. 34) este sistema puede ser rep resentado como:
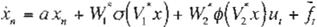
(Ec
.
36)
La RND multicapa tiene siguiente estructura:
X1 = X 2
.t? =
-,, = axn + -' a(v;,,.i) + HLef>( V2, , X )u
y=
(Ec
35)
donde:
x
1
E Dln son los estados de la RND.
u
Emv1" es el control dado.
donde:
f,
es el error de modelado.
H
(
W
2
'
\.;'* \{ son matrices constantes.
Dado que las funciones sigmoidales <J' y q¡ son uniformemente acotadas, es razonable asumir
-
que las dinámicas no-modeladas J; , satis-
facen la siguiente suposición:
Suposición 6: Existe una constante positiva
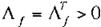 1
7
tal que:
1
7
tal que:
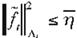
Definición 2: Sea el error de identificación:
Effi1 x>r ,
Wz.
Erxn son los pesos de la RND
que describen las conexiones de las capas ocultas y de salida.
a EITT con a < O
a
(
.
)
Effim es un vector de funciones sig moidales.
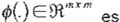 matriz diagonal, i.e..
matriz diagonal, i.e..
<P(.)
= dia<Pi cv;.l.t,),···.<P,,,< Yi.1 xi )] .
Las funciones sigmoida les usadas en a( .)y q'.>( .) cumplen con la (Ec. 12)
5.4 Preliminares
Rev
.
Centr•)
Jnv (Móx) Vol
·l. Nw11 16 EnP.-Jtin . 200 1
11
1
=x
-
x
Suposición 7: Las funciones sígmoida/es, comúnmente usadas en las RNO satisfacen la condición de Lipschitz (12):
a/
A/J, s tf/\.0!J.,,
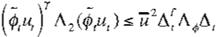
•¡ -
a,
º
º
\{
_,xi
+
va
;u,
= D"' .1x1 + v"'
donde:
2i'
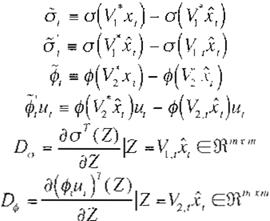
 Ir'ªel '1l .11,[(1 . > º
Ir'ªel '1l .11,[(1 . > º
qu
e
l
e
ecuación
d
e
l
a
matriz de R1catti (Ec. 38)
con
:
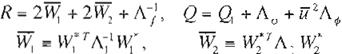
tiene
una
solución
positiva.
Estas condiciones
se
cumplen fácilmente
s1se selecct0na A como una matriz diagonal estable.
5.5 Regla de Actualzac1on de Pesos
La regla dinámica de actualización de los pesos dada por:
l
v
11
:
s;
12ll ),l
 ' l2 > O
' l2 > O
1
\l;
,t
= Vi - v;,I
,I :¡ \{ - Y¡,1
i112.1 = w2·- w2,,
./ = w1·- "·'
A 1 , ¡\2 ' t\.º Y t\.<P son matrices definidas posit i
vas.
donde:
(E
;
, 39)
Se conoce (24) que si la matriz A es estable.
K,
E" '" (i 1,···,4) son matrices definidas positivas.
el par (A, R112) es
1 '? )
controlable. el
par
P
es la solución de la ecuación matnc1al de Riccali dada por (Ec. 31).
(Q ' - ,A es observable. y la condición espe-
cial local de frecuencia o su matriz equivalente:
.o = ', W2.o = w;·,V:,o = \,(
las condiciones iniciales.
Y20
= v;·
son
A
r
R-
1
A
- Q ±[Ar R-1 - R-1 A]!{A rR-1 -
(
Ec
3
1)
se cumple, entonces la matriz de Riccati:
A
1
P
+ PA
+ P
RP
+ Q = 0
(Ec. 38)
s
,
es la función de zona muerta definida como:

 z
Oi!: o
z
Oi!: o
z
< O

µ
= ;, . (P-1 '2Q p- 112 )
"'rm
n
1
tiene una solución positiva. Siguiendo este hecho. se introduce adiciona lmente la siguiente suposición:
5 6 Análisis <1e Estah1lid;:ic1
(F7c 40)
Suposición 8: Para una matriz estable A dada. existe una matriz estrictamente positiva 01 tal
28
Teorema 3: Se considera al sistema no-lineal (Ec. 34) y la RND mult1capa (Ec. 35). Si se
R
¡;,
v
Cit
ntro
lrw
(Mt>
.
'1)
Vol J N11111. 16. Ene-Jun 2001
 -_ _,- - - - .A"l ·tículo
-_ _,- - - - .A"l ·tículo

cumplen
las suposici
ones
5-8
y
los pesos de la
RNO
se a1ustan de acuerdo con (Ec. 39). Los siguientes he chos se cumplen:
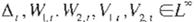
i
.
e.
el error de ident1ficac1ón
y
los pesos
de
la RNO están acotados, además
el
error de
id
enti ficación
satisface el siguiente desempeño de seguimiento:
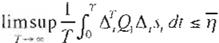
L demostración de este teorema puede ser revisada en ( 12).
5.7 Diseño del Neuro Cont.rolador
La linearización por retroalimentación es muy útil para resolver el problema de seguimiento:
Problema 4: Dada una salida deseada y,l t),
encontrar una acción de control u tal que la
planta siga una trayectoria deseada con una
donde: Q = Qr > O
Así. el seguimiento de esta trayectoria por los estados del sistema , puede formularse como:
J
,; =
minJ ,J = llx -x,¡I
(Ec
.
42)
Así, para cualquier 17> O , se tiene
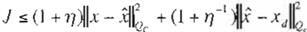
(Ec 43)
El término Jx - XJ, índica la diferencia exis tente entre los estados de la planta y los esta dos de la RND, el mínimo se
obtiene al aplicar el Teorema 3 de la sección anterior.
- - l
Ahora, seleccionando = (1 + 1'1 )Re , se
puede reformular nuestro objetivo de control
precisión aceptable (i.e. error de seguimiento
a
cotado),
mientras que todos los estados del
s
i
s
tema
y
el
control permanezcan acotados.
como: minimizar el término
Entonces:
lx -xJll). .
Para resolver este problema, se requiere establecer las siguientes suposiciones. Primero definase el vector:
Definición 4 Sea el error de seguimiento·
e = x
-
xrJ
• (11 -I) r
x/
1
)
= Yd ···Yd
y
e
l
filtro del
error.
(Ec
:
.
44)
Supos ición 9 Et vector de la trayectoria desea da xj r) es continuo y disponible para su
medición
,
y
lx/f)I[ s D con O una cofa conocida.
Definición 3 Sea la siguiente semi-norma:
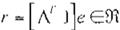
donde
:
¡\
= [A, ,
J..2 ,···,le,,.1]
y los coeficientes del vector son
apropiadamente seleccionados.
tal que
e
-o
exponencialmente
como
kJ1IQ2
1
= lim su p-
r
r:: 7 (t)Q::(t ) di
, ,,, -¡; Jo
(Ec. 41)
r
-O(s,,_1 + /\,,_, s,,_ z + ···+ A, es H unw·1 )
Así le derivada en tiempo del
filtro del error
se
rescribe como:
Rev Cer.tro
lnv
{1
h' 101 4 Núm 1(; Cn11..J1m 20()1
 Art ículo
.
. - --
Art ículo
.
. - --

5.8

 Simulaciones
Simulaciones
Xn
- X
r
. = ,\( A 1 - . ) + ···+ ( r n-1 -' ¡t-1 ) + ( A r. - X n )
Problema 5 Hallar la ley de control indirecto, que resuelva el problema de seguimiento con
x"
= (O, O, O, OJ para el sistema no-lineal TORA (Ec.
26), usando una RND.
r
= [A7 0} + (x" - x;)
¡.
= j + gu + >-:'1
(Ec. t5)
Solución 2 Se usa la RND de una capa (Ec. 35), junto con la regla de actualización de pesos (Ec. 39), para identificar al sistema y luego obtener la acción de control, utilizandolos sigu ientes valores en los parámetros :
don
de:
y
d
=
ax,1 -
x; + [ O}
Además:
W ?
Eüli x 4
'·- los vectores de pesos de la RND.
" = [l l 2) W2 = [1 2 1 21 las
condiciones iniciales de los pesos de la RND.
j -=
Vl(a(:,x)
g
= w;:, <P( v;, 2)
o( x
)
=
vación.
2-•x -0.5
(1+ e ) la función de acti-
(Ec
.
46
)
Ahora, dado que las funciones/ g no son cono cidas, se elige la acción de control uc Eüt
como:
U =
[ -J +
v
]
(Ec. 47
)
V =
-
K
v
r
- yd
rj
= 0.2,/\ = [-1 -1 -1] el valor de la cota
de la zona muerta y los valores del vector del fil tro del error.
K1 .2 == 560, K v = 0.1 los valores de las gana n cias de aprendizaje de la red y del controlador.
La simulaciones se llevaron a cabo usando el paquete matlab". Los resultados obtenidos de aplicar la acción de control se muestran el las Figuras
15-19.
 donde:
donde:
Así:
j-
= J + gu + + V - V
i
= j + ,g( [-J+ V J' + - Y,¡ - K,,r - V
g
i
·
=
f -
f + V -
v - KJ
r = -K
J
(
Ec
.
48)
Figura 15
Comportamiento
en rtemno
de
Ja ley
de
control
(Ec.
4
l
Observación 4 Sí se selecciona K.., > O el error de seguimiento es estable y además r -> O .
30
Rev Centro lnv (Méx) Vol 4
f1Jiím
16, Ena-Jvfl
20U1
 - ArtÍ<'ll /O
- ArtÍ<'ll /O

 5 8.1 Discusión de Resultados
5 8.1 Discusión de Resultados
Como se puede ver en las Figuras 11-14, la etapa de identificación del sistema no-lineal TORA fue satisfactoria. con lo cual se muestra que
una RND de una capa tiene una gran capacidad de adaptación a las no-linealidades del sistema.
F
1gurá
f
6 Control Adaorat 117 lr1dírecto par
a el estado <¡ .

F
igura 17 Contml AdaptFJIJ/P Indirecto para el estada
q
.
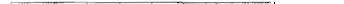
Ffgura
t 8
Control Adap1'áble Indirecto
para
el
!":Sfec' :J
8
 , IJ\/W\J\/\/\/VVV\/\/'v
, IJ\/W\J\/\/\/VVV\/\/'v
- 10
-JO
10 40 so 70
Figura 1
Control Ada,.1l"lble
lnd1recio
para el
esrac10 _
Rev
Ce
11(11J
lnv
¡
Mox
)
\/.JI 4. Nurn. 10 Ene-Jttn. 200 1
El control adaptable indirecto dado por la ley de control (Ec. 47), identifica y retroalmienta las dinámicas no-lineales de la planta, linealizando al
sistema; sin embargo, éste se ve afectado por el resultado obtenido de la identificación del sis tema TORA, cuyo error afecta directamente la acción
de control. estabiliza al sistema, no obstante este oscila mas de lo deseado, y por lo que los estados no llegan exactamente al cero, que es el valor
deseado.
Por otra parte, se presenta a las redes neu ronales dinámicas como una poderosa herra mienta para la aproximación de sistemas no-lin eales (ver
Teorema 1). aplicándolas efectiva mente en la identifica ción y control de sistemas no-lineales, como el sistema no-lineal estándar propuesto en (18)
(19).
REFERENCIAS
(1) Cybenko G, "Approximation by Superposí tion of a Sigmoidal Function", Mathematics of Control, Signals, and Systems, vol. 2, pp. 303-314, 1989.
(2) Gupta M.M. & Rao D.N., Edi ors, Neuro Control Systems. Theory and Appl ications, IEEE Press, USA, 1994.
(3) Hunt K.J.. Sbarbaro D., Zbikowski R. &
Gawthrop P.J., "Neural Networks for Con trol Systems", A Survey, Automat ica, vol. 28, pp. 1083-1112, 1992.
(4) Haykin S.. Neural Networks- A comprehen sive Foundation, Macmillan College Pub/. Co., New York. 1994.
(5} Lung L, System ldentification-Theory for the user, Prentice Hall, New Jersey, USA, 1987.
(6) Sussrnann H.J., "Uniqueness of the weights for minimal feedforwrdnets with a given input-output map", Neural Networks,
vol. 5, pp. 589-593, 1992 .
(7} Albertini F. & Sontag E.D., For neural net works function determines form, Neural Networks , vol. 6, pp. 975-990, 1993.
(8) Chen S.. B1lhngs S.A., Cowan C.F. & Grant
P.M., Practical identification of NARMAX models using radial basis functions, lntl. Journal of Control, vol. 52, pp. 1327-1350, 1990.
(9) Narendra K.S., & Parthasarathy K.. ldentifi cation and control for dynamic systems using neural networks. IEEE Trans. on Neural Networks, vol. 1, pp. 4-27, 1990
(10) Rovithakis G.A. & Chrislodoulou M.A.. "Adaptive Control of Unknown Plants Using Oynamical Neural Networks", IEEE Trans. on Syst., Man and Cybern., Vol. 24, pp. 400-41 2, 1994.
(11) Rovithal<is G.A. & Christodoulou M.A., "Direct Adaptive Regulalion of Unknown Nonlinear Dynamical System via Dynamical Neural Networks", IEEE Trans. on Syst., Man and Cybern., Vol 25, 1578-1594, 1995.
(12) Moreno M A., Control adaptable del sis tema no-lineal TORA usando redes neu ronales dinámicas. Tesis de Maestria. CIN VESTAV, 1999.
(13) Agarwal M., "A systematic classification of neural network based control", IEEE Con trol System s Magazine. vol. 17, pp 75-93, 1997.
(14) Suykens J.A. Vandewalle J.P.L & De Moor
B.L.R. Artificial Neural Networks for Model ling and Control of Non-linear Systems, Kluwer Academi c Publishers, 1997.
(15) Sbarbaro O .G.. Connectiomst feedforward networks for control of nonlinear systems. Ph. D. Thesis. Faculty of Engineering. Glas gow University, 1992.
(16) Lewis F.L., Uu K.. & Yesilderek A., "Neural net robot controller w ith guaranteed track
ing performance", IEEE Trans. on Neural Networks, vol. 6, pp. 703-715,1995.
(17) Slotine J.J. & Sanner R M., "Neural net works for adaptive control and recursive identification. a theoretical framework", Essays on Control: Perspectives in !he the ory and its app/ications, Trelelman H L. & Willems J.C. Editors. Birkhauser, Germany, 1993.
(18) Bupp R.T., Bernstein D.S. & Coppola V.T.,
'A Benchmark problem far nonlinear control design". lnt J Robust Nonlinear Control. vol.8, pp. 307-310, 1998.
(19) Wan C.J, Bernsteín D.S. & Coppola V.T., "Global stabilization of the oscillating eccentric rotor, Proc"., IEEE Conf. Decisíon and Control, Orlando, FL,1994. 4024-4029 . Also. Nonlinear Dyn, 10,
49-62 , 1996.
(20) Jiang Z .. Híll D.J. & Guo Y., "Stabilization
and tracking via output feedback for the nonlinear benchmark system", Automatica, vol.34, núm.7, pp 907-915, 1998.
(21) Jagannathan S & Lew1s F.L., "ldentification
of nonlinear dynamícal systems using multi layered neural networkstt. Automatica . vol.32 . núm.12,pp. 1707- 1712. 1996.
(22) Kosmatopoulos E.B.. Polycarpou M.M., Christodoulou M.A. & loannpu P.A.. "High Order Neural Network Structures for ldenti fication of Oynamical
Systems", IEEE Trans. on Neural Networks, Vol.6, Núm. 2.
pp. 442-431 . 1995.
(23) Yu W., Poznyak A.S., "lndirect Adaptíve Control via Parallel Dynam1c Neural Net works". IEE Proceedings - Control Theory and Applications, Vol. 37, Núm. 1. 1999
(24) Willems J.C., "Least squares optimal con trol and algebraic Riccati equations", IEEE Trans on Automatíc Control, Vol. 16.
Núm 6. pp 621-634, 1971.
(25) Widrow B. & Steans S D.. Adaptive Signa/ Processmg , Prentice-Hall. Englewood Cliffs, NJ,1985.
(26) Kosmatopo ulos E.B., Christodoulou M.A. & loannpu P.A., "Dynam1cal Neural Networks that Ensure Exponential ldenlification Errror Convergence''. Neural Networks, Vol.1O,
(27) Poznyak, AS & Sánchez, E.N, ' Nonltnear system approximation by neural networks error stability analysis", In/. J. lntefl. Autom Sort Comput. vol 1, pp. 247-258 , 1995.
(28) Poznyak A.S., Yu W. . Sanchez E.N. & Pérez J.P . "Stabihty Analysis of Dynamic Neural Control", Expert System with Appli catíons. Vol.14, Núm. 1, 227 -236, 1998
![]() M
A.
Moreno-Armendariz
1
,
W. Yu-Litt
& A S Poznyak z
M
A.
Moreno-Armendariz
1
,
W. Yu-Litt
& A S Poznyak z



 .,-
.,-



 2. Control Indirecto: En esta estructura (14), primero un neuro-identif1cador estima el comportam iento de la planta, usando como información
únicamenle la salida del sis tema, luego el neuro-controlador es diseña do con base en el modelo identificado , ver Figura 9. La acción de control
busca que la planta siga la señal de referencia
2. Control Indirecto: En esta estructura (14), primero un neuro-identif1cador estima el comportam iento de la planta, usando como información
únicamenle la salida del sis tema, luego el neuro-controlador es diseña do con base en el modelo identificado , ver Figura 9. La acción de control
busca que la planta siga la señal de referencia


 M + m
M + m

 w e-
w e-
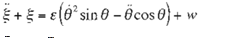 e
= -E z; cose + u
e
= -E z; cose + u
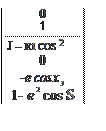 ft::
r;
.
25)
ft::
r;
.
25)