Análisis experimental de la superposición de información en espacios de memoria aleatoria
A.
T.
Ramos Fonseca & J. F1gueroa Nazuno Centro de Investigación en Computacrón-IPN Laboratorio de Cómputo Distriburdo y Paralelo. E-mal/ <sadness@compaq .net.mx>
<j
fn@pollux.mx>
RESUMEN
En este trabajo se presenta un modelo de almacenamiento de información que es especiaimente ade cuado para sistemas neurocomputacionales no
supervisados. Nuestro modelo utiliza como fundamento teórico el Teorema de Ramsey. Se demuestra experimentalmente que en una matriz discreta generada
aleatoriamente y lo suficientemente grande (dependiente de 111 i: 11). es posible encontrar cualquier matriz discreta de tamaño m x n. La probabilidad p( <p e A1) de encontrar una submatriz de tamaño 11; x n dentro de un
Espacio de Memoria Aleatoria específico aumenta al permitir grados de error acotado. Introducimos entonces el concepto de patrón de información.
También aplicamos diferentes transformaciones lineales a la matriz original, lo cual amplía el espacio de búsqueda y por lo tanto también aumenta la
probabilidad
p(rp e M). El modelo se implementa utilizando memorias de cuatro estados y se demuestra una de sus
principales características: la superposición de información. Un mismo elemento físico de memoria se uti liza para almacenar varios patrones de
información a un mismo tiempo. Se encuentra que para patrones de información de dimensión cuadrada 111 x 111 el máximo grado de superposición
que se puede obtener es ( 2m - 1)2 y que en un EMA de tamaño relativamente pequeño es posible almacenar una gran cantidad de patrones de
información
Palabras clave: Teorema de Ramsey, matoz discreta, Espacio de memona aleatoria, patrón de informa
ción, superposición de información.
ABSTRACT
This works presents an information storag1ng model, specíally useful for neurocomputmg non supervised systems. Our model uses Ramsey Theorem as a
theoretical foundation. lt is experimentaly shown that in a discreet matrix randomly generated and large enough (dependan!of m x n) it is
possible to find any dis creet matrix of 111 x 11 siz.e. The probability p( <p e fvf) of finding a
sub-matrix of /11 - /1 siz.e within an specific Random Memory Space increases when allowing limited error degrees. We introduce then
the concept of information pattern. We also apply d1verse lineal transformations to the original matrix, which lenghtens the space of search and also
increaseslhe probability p( <p e M). The model is implemented using memo ries of tour stages and one of its main
features is proven: information superposition. One sole physícal element of memory is used to store several information patterns al the same time. P is
found that for infor mation patterns of squared dimensíon 111 r 11 the maximum degree of attainable superposition is ( 2m - 1) 2 and that in an EMA relatively small can be stored a great amount of information patterns.
Keywords: Ramsey lheorem, discreet matrix, Random Memory Space, informa/ion pattem, informa/ion
superposítion.
Rev
C
entro
tri
v
(Méx)
Vol 5
.
N11m
s
17-16
,
Ju/ 2001-Jun
2002
29

J¡)
 1 INTRODUCCION
1 INTRODUCCION
La necesidad de modelos de representación de grandes cantidades de información es carac terística dentro del campo de la neurocompu tación2. El
objetivo de este trabajo es plantear un modelo de almacenamiento de información: el Espacio de Memoria Aleatoria (EMA). Este modelo
tiene fundamento teórico en el Teorema de Ramsey, el cual de manera general afirma que si un grafo contiene suficientes vértices (valor dependiente de
k), entonces debe con tener un conjunto completo o un conjunto inde pendiente de tamaño k4 .
Nuestro modelo parte de la suposición de que dentro de una matriz discreta de un tamaño¡x j suficientemente grande y con
valores genera
dos aleatoriamente, es posible encontrar cual qL1ier matriz discreta de tamaño /11 x 11 que se desee. con una probabilidad
directamente pro
porcional ar tamaño de la matriz aleatoria e
inversamente proporcional al tamaño de la sub matriz que se busca.
De manera general, el modelo consiste en una matriz binaria M generada aleatoriamente. La información que se pretende buscar y alma cenar es
sometida a una transformación me diante la cual una cadena binaria :; se convierte en una matriz q>. Se efectúa una búsqueda de <p en cada una de las transformaciones lineales definidas para la matriz M, hasta que se encuentra una submatriz 0 de M que es igual a
<p. En ese momento se "marca" un elemento de memoria que tiene una posición específica den tro de 0 con una referencia a la transformación en que
fue encontrada la submatriz. Esto per mite la recuperación efectiva de todas las matri ces <p y por lo tanto de toda la "información
almacenada".
Dado que la utilización de los elementos de una submatriz e por una matriz <p1 no impide
que algunos de estos mismos elementos sean utilizados por algunas otras matrices lf>:?,<Q,,,. .,c:p., es posible que varias matrices q>¡
compartan un
mismo espacio físico de memoria,dando lugar a la superposición de información (Figura 1).
|
o
|
|
1
|
|
|
1
|
1
|
|
o
|
o
|
1
|
o
|
|
o
|
1
|
o
|
o
|
|
1
|
1
|
o
|
o
|
1
|
1
|
o
|
1
|
|
|
1
|
|
1
|
1
|
o
|
1
|
o
|
1
|
1
|
1
|
o
|
|
|
1
|
o
|
1
|
o
|
o
|
1
|
1
|
|
o
|
1
|
o
|
1
|
|
F
igure
1 St¡pe1posic1011 :Je info1mac; ·,n en una
matru al
·
atona
S1 permitimos que la búsqueda de matrices <P en el Espacio de Memoria Aleatoria presente errores acotados, es decir, si permitimos que
exista una diferencia acotada entre <¡> y alguna
submatriz e. entonces la probabilidad de encon trar edentro de M aumenta. Estamos hablando
entonces de patrones de información, dado que nuestro interés no se centra en una repre sentación exacta de una estructura de informa ción pero sí en
una estructura fundamental que debe conservarse y que es significativa dentro de algún paradigma computacional. En la sec ción 5 demostramos
expenmentalmente cómo el introducir el concepto de patrón de informa
ción aumenta dramáticamente la probabilidad de encontrar dentro de M alguna e que con
serve la estructura fundamentalde una matriz <p.
Aunque el cálculo del tamaño de la matriz aleatoria para un tamaño especifico de subma trices m x 11 permanece desconocido, nos pro
ponemos: 1) Encontrar de manera experimental una relación entre los tamaños de las matrices de tal manera que tengamos la certeza de qu dado un tamaño
de submatriz, será posible encontrar cualquier instancia de este tamaño dentro de la matriz aleatoria; 2) Estudiar el com portamiento del modelo
cuando se pre1ende almacenar grandes cantidades de información y
3) Proponer elmodelo como un paradigma efec tivo y eficiente para sistemas neurocomputa cionales.
2 TEOREMA DE R;MSE
En el campo de las matemáticas, existen numerosos teoremas que afirman, de manera general, que todo sistema de una cierta clase
R
\
Centro In, (Mé,..) Vo 5 Num:s 17 18 Ju/ 2001 Jun 2002
= - ---- = - - ------. . =-
- - lff. 1íi;.uto:
contiene un subsistema con un grado de organi zación mayor que el sistema original1.
Los llamados "Teoremas de tipo Ramsey" prueban esta afirmación tomando como objetos de análisis diferentes entes matemáticos: con juntos y grafos
(Ramsey)7. ecuaciones (Schur, Rado)8·9, progresiones aritméticas (Van der
Dado cualquier coloreo en r de [n l2 , si existe i,
1 s i r, y un conjunto T \:: [n). ITI = 1, tal que [TF
es monocromático en i. entonces escribimos
n (11 .•.. .l,)
La función de Ramsey R(l1,....1,) denota el mínimo valor de n tal que la proposición anterior
Waerden) 12
secuencias frnitas formadas de
es cierta.
conjuntos finitos (Hales-Jewett)5. espacios vec
toriales (Graham-Lib-Rolhschild)3, etc. Estos teoremas conforman lo que se conoce de manera genera l como la Teoría de Ramsey, una subdisciplina dentro
de las matemáticas discre tas. La mayoría de estos teoremas afirman que un coloreado en r de cualquier estructura lo sufi cientemente grande contiene
una subest ructura monocromática de cierto tamaño. En términos de la teoría de grafos, si un grafo contiene sufi cientes vértices (un número
dependient e de k). entonces debe contener o un conjunto completo o un conjunto independiente de vértices de tamaño k.
Resulta conveniente mencionar que algunos teoremas matemáticos como el de Bolzano Weierstrass. que afirma que dentro de cualquier secuencia acotada de
números complejos existe una subsecuencia convergente, entran dentro de la clase de teoremas mencionada en1, pero no conforman parte de la Teoría de
Ram sey.
Para dar una definición formal rntroducimos la siguiente notación.
l+ :: {1,2,...}== los enteros positivos.
{n] = {1,...,n}, n ,+ es un conjunto arbitrar io de
cardinalidad n.
[A)k = {B:B e A, IBI = k}.
Un coloreado en r de un conjunto S es un mapeo
( : S -7 (r]
Para s E S, a (<s) se le denomina el color de s. y decimos que un conjunto T e S es
monocromático bajo ( si (ú> es constante en T, esto es
(<1
)
= r¡ V t E T, T \:: S. i constante
.He11 C:«1 tro.1r1v Mx Vol 5. Nvr · f 7 78 Ju/ 2001-JUr• WO.
La generalización del caso anterior es cuan do consideramos el coloreado en r de ln]k, donde k es un entero arbitrario.
Definimos n (11.....V si, para todo colorea do en r de [nJ J.. , existe i, 1 s isr. y un conjunto T
f n l . ITI= 1, tal que [T)k es monocromático en i.
En este caso, la función de Ramsey para conjuntos de cardinalidad k se indica por Rk
R 01·····l) = mini n0 : para n 11,1, n (11..•.,1,)k}
El Teorema de Ramsey afirma que la función Rk está bien definida: esto es, para todo k,1¡,....I,. existe n0 talque para n 110 se cumple
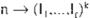
Se han desarrollado varias demostraciones de éste teorema . La demostración original a cargo de Frank P. Ramsey toma tanto el caso de un conjunto
infinito como el de su análogo finito7.
El cálculo de los valores exactos de la función de Ramsey R(k.I) para valores pequeños de k,I ha significado tremendos esfuerzos, sin embar go, hasta
la fecha se conocen solamente los valores exactos y las cotas superiores e inferio res publicadas en6.
Nuestro interés se encuentra en probar experimentalmente la idea básica del Teorema de Ramsey en matríces discretas y utilizar esta poderosa idea como
fundamento para un nuevo paradigma de almacenamiento de información en sistemas neurocomputacionales. Para ello debemos probar experimentalmente que en
una matriz discreta M de un tamaño suficientemente grande (posiblemente generada de manera
aleatoria) podemos encontrar cualquier matriz
J I
Artículo
_. '
_ _ - - ':'° _ - - -- - _

 discreta cp de un tamaño menor que M, con una probabilidad que aumenta conforme el tamaño de M es mayor.
discreta cp de un tamaño menor que M, con una probabilidad que aumenta conforme el tamaño de M es mayor.
p (cp e M) aumenta si M aumenta en tamaño 3.EL MODELO FORMAL.
Definimos un Espacio de Memoria Aleatoria
(EMA) corno la tupla <M.E.S.T.0.í,€>. M es una matriz bidimensional, E. T. e y r son conjuntos. S es un par ordenado y e es un natural.
M es una matriz de tamaño ix j que contiene estructuras de la forma (v,r) en donde v E E. r es una referencia a algún < E
T. E y T son conjun tos finitos y
l.:. e (el conjunto de tos números discretos) Definimos elconjunto de valores base E' como E' = {e :c c E A IE'f :::: IE J/ 2 1
Los valores v son generados inicialmenle de manera aleatoria y cumplen con la restricción
V E E'
Definimos la matriz de valores M, corno aquella que se obtiene al eliminar el elemento r de cada una de tas estructuras (v,r) de la matriz
M. La matriz de referencias M, es la que se obtiene aleliminar elelemento v de cada una de las estructuras (v.r) de la matriz M.
La correspondencia entre un elemento MV,J y uno !\t,, es permanente, es decir, un elemento
0 es el conjunto de submatrices de tamaño m x
n
contenidas en las matrices i:(M,.) de Ml"
donde cada elemento 0,y en(:} se encuentra for mado por el conjunto Pxv de elementos
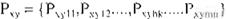
y donde cada P,yhl.. es un valor v en una •(M,.) con posición en (h.k) dado er- origen relativo (x,y).
Dado algún 0,, •+ E e. donde a,b E l , sí se cumplen las condiciones lal< m y lbl < n, y sea
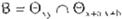
entonces la siguiente proposición es válida:
B o
Puede observarse que las submatrices 0,y y 0Ha , ¡, contienen elementos Prhk en común dentro de alguna matriz -r(lvU. La cantidad de elementos
compartida dentro de 1(M,.) por este par es
1 B !:::: ( abs( 111 - abs(a)) 1 1 nb(n - abs(b) J 1
donde ab(x) es el valor absoluto de x.
El número de submatnces 0) en M\ está dado por
e = l(1 - 111 + i) (j - n + 1)J t
M ,,
1
está relacionado en todo momento sola
mente con el elemento M,u·
S = tm.n) donde m.n E 1•.
T es un conjunto de transformaciones lineales -r
que operan sobre M. M,. y M,, produciendo los conju:>tos de matrices M'. M'. y M', .
M'= {-r(M) :i:e T)
M\ = { t(MV) : '( E T 1
1W, = { t(Mr) : i: E TJ
32
donde t es el número de transformac iones
lineales aplicables a M.
t = IT I
Un patrón de entrada <p es una matriz binaria de tamaño 111 r n. Al aplicar las transforma ciones lineales i: a la matriz M,se incrementa
la probabilidad de ocurrencia de <p
p(<p E 0)
La búsqueda de un patrón q> en el EMA es un mapeo del plano de entrada <P a un plano r(Mv)
Rev
Ce
ntro tn
v (
Méx) Vol
.
5
,
Nums 17
-18
.
Jul
.
2001-JtJri
.
200
2
..... .. --. .
Artículo
;

para alguna 1. obteniendo una submatriz e,Y e
e. que no necesariamente es idéntica a <p. y el número de elementos en que difieren queda determinado por
m- ! 11- l
t((jl.0,y) = L 2: </> (1 1) \¡! <:;)"Y (\ +\;.y+ ll
k=O 1=0
donde \ji es un operador de equivalencia, que se define de la siguiente manera:
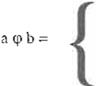 O si nRb
O si nRb
que almacenan algún patrón de entrada <¡> con f(<¡>,0,y) < ::: € y que comparten al elemento M.;¡ de M,.. Para patrones de entrada <p
con geometría cuadrada r11 x 111 el máximo grado de superposición queda determinado por
(2m - 1)2
Debido a que al almacenar un patrón, se "marca" un elemento (v,r), el número maximo de patrones que se puede almacenar en un espa cio de memoria
aleatoria es ;x j. el tamaño de la matriz M.
a e i::.· . b e E de or r 1 r.l.?.'1era
La relación R: E. E es reflexiva y mantiene una correspondencia 1 a 2.
Para que el patrón de entrada cp sea asignado a la submatriz 0,), son condiciones necesarias
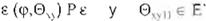
debido a que al momento de asignarse. el valor v de Qxy11es sustituido por
w E r:. vRw. v ;é w
y este elemento no podrá utilizarse para marcar algún otro patrón de entrada 1p,. Adicional
mente, alelemento r, con el que e,,11 forma una
estructura (v,r) en !\I, le debe ser asignada una referencia a la transformación 't para la cual e,)'
es una submatriz de -c(MJ.
r es el conjunto de patrones que se almacenan en el [:!\.JA dado un conjunto il de patrones de entrada
n\- l n- 1
l'= IE\1:( L 1<t>ll.n 'l' 0» '' L.> ·" )T c,
k=O l-=O
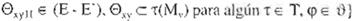
El grado de superposición de un elemento M,i. es decir, una estructura (v,r) con posición i. j en la matriz M. es el número de submatrices 0xy
4. IMPLEMENTAC IÓN.
M es implementada como un vector de n Matri· ces < M1.M2.....M0) de tamaño ix j. Dado que deseamos manejar patrones binarios de
infor mación, cada elemento de M, es una unidad de
memoria de 4 estados:
E = (O. l , 0*, !*) y E·(o. n
El valor de 11 depende de el número de trans formaciones -r definidas sobre M. M,. y M, (t :::: ITI). En nuestros experimentos decidimos uti
lizar dos coniuntos de transformaciones linea les. El primero consta de 16 transformaciones que se obtienen de la siguiente manera:
1. 4 diferentes rotaciones: 90, 180 y 270 grados.
2. A cada una de estas rotaciones. traslación en su eje horizontal.
3. A cada una de las 8 transformaciones anteriores, inversión de los valores lógicos de la matriz.
Dado que cada elemento de memoria puede codificar cuatro diferentes estados, un vector de dos elementos puede codificar estas dieciseis
transformaciones. Decimos que
M_. = M 1
M,:;:. (M1,M3)
y un elemenco (una estructurn) de M con posición i j
e define por
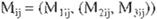
donde v = M1.. v r = (M,. M ..).

 1.Artícrt!ir
-
-.- - t-
1.Artícrt!ir
-
-.- - t-
- - .- -_ • .-.i: - -

El segundo conjunto incluye 48 transforma ciones. 3 de las cuales llamamos básicas:
1. La matriz original.
2. Intercambiando pares de renglones.
3. Intercambiando pares de columnas.
4. A cada una de las tres anteriores, se le apli can las 16 transformaciones del primer con junto.
En este caso, definimos cuatro matrices: M1 •
M2 • M-' y M.:
M,= M1
M,= (M,.,M 3,M4)
Mij = (M11 ' (M1.,. M3;_¡.M4))
Tanto el tamaño irj de M.el tamaño "'x" de los patrones de entrada q> y el grado de error e per mitido en la búsqueda de patrones
dentro de Mv
quedan como parámetros para el analisis experimental. Sin embargo, en nuestros ex.peri mentos restringimos las dimensiones de M y m
a espacios cuadrados , es decir. i =j y 111 ::: n.
5 ANALISIS EXPERIMEI'.TA .
El primer experimento consistió en medir las fre cuencias de ocurrencia de los elementos de un
conjunto de patrones de entrada generados de manera aleatoria . El objetivo es encontrar expe rimentalmente una relación entre el tamaño de la matriz
M, el tamaño de los patrones <p y el grado de error permitido e. de tal manera que tengamos la certeza de que cualquier patrón de entrada será
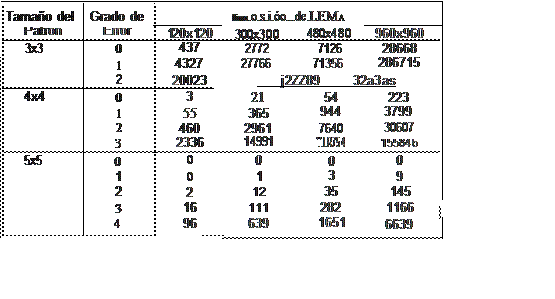
encontrado dentro un Espacio de Memoria Aleatoria particular. Los resultados se muestran en las Tablas 1 y 2 para EMA's de 16 y 48 transformaciones
respectivamente.
A continuación medimos una de las carac ter ísticas mas importantes del modelo: la super posición de información. Para ello generamos n de patrones
de manera aleatoria, efectuamos la búsqueda y asignación de cada patrón y poste riormente medimos, para cada estructura (v,t) en M. cuántos patrones
eslán ocupando dicha estructura (el grado de superposición). El valor de n debe ser tal que se logren encontrar todos los patrones dentro del EMA. Las
Tablas 3 y 4 muestran el número de estructuras que presen tan determinado grado de superposición dados un tamaño de EMA. un tamaño de patrón de
entrada, un número n de patrones, y un grado de error e particular. Estos resultados son los obtenidos como media de 50 repeticiones del experimento
para EMA's de 16 transforma ciones.
Tabl
a
1 Re
s
ultados e
xpe
n
m
e
n
teles
de
la ;recvencm de
o
cur
rende
etc
U
ll
parró
n
i
;mario dentro
d
e un
E
MA
utd1
z
arido
16
t
1anstor mac1ones
(p
!O
medios sobre 5
0
pat
,.
o
.
ne
s
)
.
Re
v
Cr-
1.ro lnv (Me,() Vol 5 N<Jms. 1b Ju.' 2001-Jun. 2 002
Artf(·ulo

Tabla 2. Result9dos expenrmmtriles de la frecuencia da ocurrencia di; un patrór1 binario dt.ntro de Uíl EMA lltdiza-ido 48 transformaciones
(promedio::: sobre 50 r;c1tronf..S)
|
Tamaño del Patrón
|
Grado de Error
|
Dimensión del EMA
|
|
-
|
|
|
120x120
|
300x300
|
480x480
|
960x960
|
|
|
3x3
|
o
|
1307
|
8341
|
21445
|
86008
|
|
|
12983
|
83264
|
214137
|
859308
|
|
|
1
|
|
|
2
|
59928
|
383249
|
984917
|
3957367
|
|
|
4x4
|
o
|
10
|
65
|
166
|
673
|
|
|
1
|
171
|
1097
|
2824
|
11338
|
|
|
2
|
1394
|
8825
|
22867
|
91888
|
|
|
3
|
7036
|
45029
|
116272
|
466911
|
|
|
5x5
|
o
1
|
o o
o 3
|
o
9
|
2
33
|
|
|
2
|
5
|
38
|
107
|
430
|
|
|
3
|
50
|
325
|
855
|
3461
|
|
|
4
|
297
|
1923
|
4973
|
19963
|
|
Tabla
3 Resultados
experrmentDl&s
de
supe1posic16n
de
ínfot
mec1611
en Espacios de Memoria Aleatoria
.
 Resultados
pa
1
a
mAtnces
de
tamann
120x
J
2U
r.:on 16 tre11sformac1ones
Resultados
pa
1
a
mAtnces
de
tamann
120x
J
2U
r.:on 16 tre11sformac1ones
|
Patrón
|
Error
|
Patrones
|
Oº
|
1º
|
2º
|
3º
|
4º
|
5º
|
6º
|
7º
|
8º
|
9º
|
10º
|
|
3x3
|
o
|
250
|
13108
|
707
|
321
|
181
|
61
|
18
|
4
|
o
|
o
|
o
|
o
|
|
|
|
500
|
12503
|
740
|
437
|
298
|
213
|
133
|
58
|
17
|
1
|
o
|
o
|
|
|
|
1000
|
11426
|
939
|
553
|
450
|
297
|
304
|
226
|
115
|
74
|
16
|
o
|
|
4x4
|
1
|
250
|
11306
|
2366
|
572
|
136
|
18
|
2
|
o
|
o
|
o
|
o
|
o
|
|
|
|
500
|
9074
|
3445
|
1305
|
414
|
118
|
35
|
7
|
2
|
o
|
o
|
o
|
|
|
|
1000
|
6571
|
3676
|
1941
|
1144
|
591
|
293
|
122
|
48
|
13
|
1
|
o
|
|
5x5
|
2
|
250
|
10101
|
3335
|
845
|
91
|
8
|
o
|
o
|
o
|
o
|
o
|
o
|
|
|
|
500
|
6690
|
5070
|
2006
|
545
|
87
|
2
|
o
|
o
|
o
|
o
|
o
|
|
|
|
1000
|
3417
|
4705
|
3456
|
1822
|
733
|
210
|
42
|
12
|
3
|
o
|
o
|
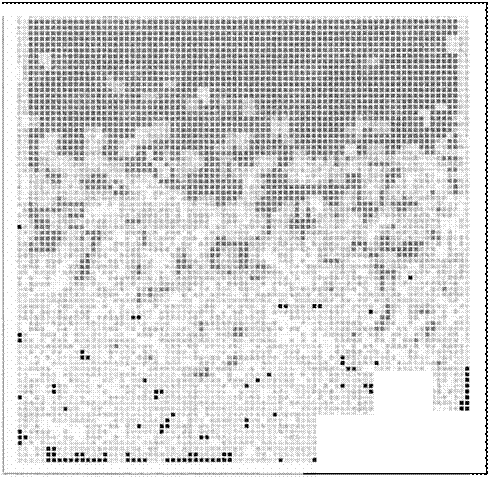
Para dar una mejor idea de qué manera se lleva a cabo físicamente la superposición de información en los Espacios de Memoria Aleato ria, obséNense las
Figuras 2, y 3. Estas figuras son matrices que representan los grados de superposición alcanzados en los elementos de un EMA experimental de 80x801
elcual almace-
na patrones de dimensión 3x3 sin error permiti do, esto es e = O. Cada color codifica un grado de superposición diferente . De esta manera
po demos observar la evolución de un EMA res pecto a la perspectiva de la superposición de información.
Rov. Centro
lr1v
(Mé>:) Vol
5 Nt1ms 17 18, JU/ 2001-Jun 2002 35


 fi
i
/
i_(!,ulu
fi
i
/
i_(!,ulu
- ·
 Tabla
4 R
e
ultad() e l(penm
em
al
es
d
e su
perp
os1c
1
1..
m
de
mlorm
ac1o
n
en
Esp8c1
o
s
d
e
Me
m
o
n
a
A
r
e
af1
)n
a
.
Tabla
4 R
e
ultad() e l(penm
em
al
es
d
e su
perp
os1c
1
1..
m
de
mlorm
ac1o
n
en
Esp8c1
o
s
d
e
Me
m
o
n
a
A
r
e
af1
)n
a
.
 Resultados
par:? ma 1íces
de
tameño
30Ux300
con
16
tra •s1ormac1onFs
Resultados
par:? ma 1íces
de
tameño
30Ux300
con
16
tra •s1ormac1onFs
|
Patrón
|
Error
|
Patrones
|
Oº
|
1º
|
2º
|
3º
|
4"
|
5º
|
6º
|
7°
|
8º
|
9º
|
10º
|
|
3x3 o t:¡{)()
|
87fi.68
|
107fi
|
f\¡:\{)
|
F\'<
|
171
|
48
1 2 o o o
|
|
|
|
1000
|
|
86893
|
986
|
578
|
533
|
341
|
321
|
203
|
96
|
41
|
8
|
o
|
|
|
|
2000
|
|
8533"5
|
992
|
643
|
755
|
498
|
460
|
550
|
321
|
276
|
150
|
o
|
|
4x4
|
1
|
500
|
|
84458
|
3805
|
1226
|
354
|
111
|
39
|
7
|
o
|
o
|
o
|
o
|
|
|
|
1000
|
|
81650
|
4207
|
2090
|
1099
|
586
|
261
|
83
|
23
|
1
|
o
|
o
|
|
-·.---..-..
5x5
|
2
|
2000
500
|
|
78251
78338
|
4366
10851
|
2371
784
|
165--·--
27
|
1259
o
|
850
o
|
55
8
o
|
3
7
6
o
|
185
o
|
97
o
|
21
o
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

o 2 3 4 5 6 7 8 9 10 l l 12 J 3 l 4 150 +

b)
Figur
a
2 a
)
Código
d
e
c
ol
ores
pa
r
a
l
a&
fJ
q
ur
a
.s
2
y
3
. b
)
Vísualizac1
ón
t1e
superpusic16n de información
p
a
1
a
u
n
1=MA de 80x80
y
4
0
0
0
pat
ron
es
d
e
tam
a
ñ
o
3
x3
.
Re1 Cenfrolm (Mx) Vol 5. Nóms í7-18. Ju/ 2001-Jun 2002
 Artículo
·
Artículo
·
....
' ::
.....•.
·-··l..·· ·.:
Fi
gu
ra
3
_
\/1soalizacrón de superposiC1ón de
mformac1ón
p
am un EMA de BOxBO
y
6000 patrones de tamai?o Jx3. El código de co
l
ores se observa en
h.
Figura
2
.
Table 5 Resultados
experimentab·s
de
superposición
de
111formac1ón
e
n Espacio
s
clti
Memor i
e
Afeato ia Resultados para matríces de
tamaño
120x120
con
16 fra1sformaciones
y
ntírnero
de patmne:o •'ercano a la
capa
cidad
m
á
xima
efe a/macenamí&nto


|
Tamaño del Patrón
|
Grado de Error
|
Número de Patrones
|
Grados de Superposición
|
|
Oº
|
1º
|
2º
|
3º
|
4º
|
5º
|
6º
|
7°
|
8º
|
9º
|
1Oº
|
|
3x3
|
o
|
500
|
87668
|
1075
|
660
|
363
|
171.
|
48
|
13
|
2
|
o
|
o
|
o
|
|
1000
|
86893
|
986
|
578
|
533
|
341
|
321
|
203
|
96
|
41
|
8
|
o
|
|
2000
|
85335
|
992
|
643
|
755
|
498
|
460
|
550
|
321
|
276
|
150
|
o
|
|
4x4
|
1
|
500
|
84458
|
3805
|
1226
|
354
|
111
|
39
|
7
|
o
|
o
|
b
|
o
|
|
1000
|
81650
|
4207
|
2090
|
1099
|
586
|
261
|
83
|
23
|
1
|
|
o
|
o
|
|
|
|
2000
|
78251
|
4366
|
2371
|
1658
|
1259
|
850
|
558
|
375
|
185
|
97
|
21
|
|
5x5
|
2
|
500
|
78338
|
10851
|
784
|
27
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
|
1000
|
68467
52005
|
18443
|
2744
|
3165
|
31
|
o
|
o
|
o
|
o
-b
|
o
|
o
|
|
2000
|
28124
|
8016
|
1610
|
215
|
26
|
4
|
o·-
|
o
|
o
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- -
F<ev
Ce
ntr
o
lnv
¡Méx)
Vol 5. Nums 17-tB. Jul 2001-Jun. 2002 37
,tÜ;ríe.ufo
-

 1.,, • , • Tabla 5.
1.,, • , • Tabla 5.
|
1000
|
86893
|
986
|
578
|
533
|
341
|
321
|
203
|
96
|
41
|
8
|
o
|
|
2000
|
85335
|
992
|
643
|
755
|
498
|
460
|
550
|
321
|
276
|
150
|
o
|
|
500
|
84458
|
3805
|
1226
|
354
|
111
|
39
|
7
|
o
|
o
|
o
|
o
|
|
1000
2000
|
81650
78251
|
4207
4366
|
2090
2371
|
1099
1658
|
586
1259
|
261
850
|
83
558
|
23
376
|
1
185
|
o
97
|
o-
21
|
|
500
|
78338
|
10851 784 27 o o o o o o o
18443 2744 3165 31 o o o o o o
28124 8016 1610 215 26 4 o o o o
|
|
1000
|
68467
|
|
2000
|
52005
|
El experimento realizado para la obtención de las Figuras 2 y 3 sugiere que un EMA puede almacenar muchos más patrones de entrada que los utilizados
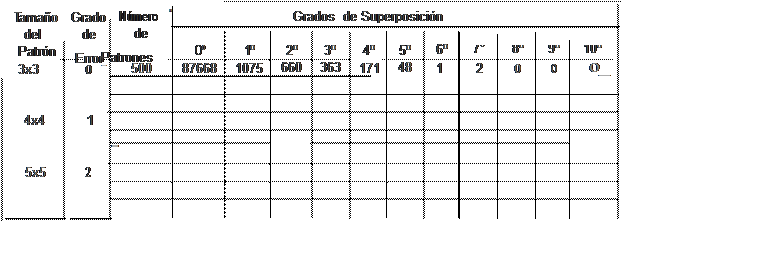
para generar las Tablas 3 y 4 . Por ello realizamos un último experimento para encontrar los mayores niveles de superposición alcanzados
cuando se genera un gran número de patrones. número cercano a la capacidad máxima de almacenamiento del EMA. La Tabla
5 muestra los resultados obtenidos para un EMA de 120x120. Se utilizan únicamente patro nes de tamaño 3x3 y 4x4, debido a que no es posible encontrar
todos los patrones generados cuando su tamaño es 5x5.
r
INTERPl1E JACIÓN DE LOS RESULTADOS .
En las Tablas 2 y 3 podemos observar como la probabilidad de encontrar un patrón de entrada dentro de un EMA de tamaño particular aumen ta de manera
directamente proporcional al Ta maño del EMA y el grado de error permitido e inversamente proporcional al tamaño del patrón de entrada .
las Tablas 3. 4 y 5 junto con las Figuras 2 y 3 demuestran en forma muy clara la superposi ción de información que tiene lugar en cada ele
mento de memoria física dentro de un EMA. Podemos observar cuantitativa y cualitativa mente cómo un mismo elemento físico de alma
cenamiento puede utilizarse para almacenar mas información de la que es capaz al utilizar un modelo convencional de memoria.
38
En la Sección 3 se afirma que el máximo grado de superposición posible cuando uli lizamos patrones de entrada con geometría cuadrada m x m es (2m - J )2, es decir, teórica mente es posible que (2m - J )2 patrones
estén utilizando un mismo elemento de memoria físi ca. En la práctica vemos que el máximo grado de superposición es mucho menor,aún cuando el número
de patrones almacenados es muy cercano a la capacidad máxima del EMA, esto es debido a que el cálculo de el grado máximo de superposición obedece a una
distribución específica de los patrones en las diferentes transformaciones de las matrices y de la posi ción dentro de estas transformaciones,
distribu ción que no tiene ninguna certeza de lograrse dada la naturaleza aleatoria de la matriz de valores.
Podemos efectuar un análisis de la capaci dad teórica de almacenamiento de información en un EMA particular y comparar este valor con su análogo
utilizando un modelo convencional de memoria. Esto es. en un EMA de ix i que al macena patrones binarios de entrada de tamaño m x m (utilizando memorias físicas de cuatro estados). teóricamente podemos almacenar i x i patrones, por lo tanto podemos almacenar ¡l x m1 bits,es decir,se pueden codificar
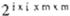
combinaciones . Cuando el mismo espacio de memoria física se emplea de manera conven-
cional podemos almacenar ix i elementos de memoria de 4 estados, es decir 2 x i2 bits, con los cuales se
pueden codificar
combinaciones. La diferencia es clara. y puede observarse que se aumenta notablemente la capacidad de almacenamiento al aumentar el tamaño de el patrón de
entrada. Si por ejemplo. el tamaño de los patrones de entrada aumenta a (m+1) x (111+ 1) la cantidad de combinaciones que se
pueden obtener es
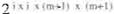
lo que significa
2 • \ 1 > (2m..-I)
veces que la cantidad obtenida con patrones de tamaño 111 x 111.
Sin embargo, no es posible aumentar arbi trariamente el tamaño de los patrones de entra da, se tiene que lograr un balance entre la capacidad de
almacenamiento y la probabilidad de encontrar dichos patrones.
7. CONCLUSIONES.
El modelo de Espacios de Memoria Aleatoria para el almacenamiento de información presen ta varias características interesantes. entre las que se destacan
su naturaleza primariamente aleatoria y la superposición de información. En la actualidad el paradigma de la computación cuántica emplea el concepto de
superposición de estados utilizando entidades abstractas lla madas qbils como elemento fundamenta l de al macenamiento (13). Aparentemente el empleo de
una misma entidad rísica para representar diferentes cosas (estados. información, etc.) de manera simultánea es un concepto importante para el desarrollo
de nuevos paradigmas computacionales.
La orientación hacia los procesos de almace namiento y la sencilla manipulación de informa ción son características que dist inguen a los Espacios de
Memoria Aleatoria de otros mode los de almacenamiento centrados en la repre-
Rev
.
C
entr
u
tn
v
( Mex)
V1)/. 5 Nc1m.; 1l-18 Jvl 200 1 Jun 4002
sentación directa de información. Sin embargo, estos sencillos procesos y manipulaciones pro porcionan una gran capacidad de almace namiento dinámico de
información.
8 REFERENCIAS.
1. Burkill. H. & Mirsky, L. Motonicity. J. Math.
Anal. Appl
.
1973.
2. Figueroa-Nazuno J., Mayal-Cuevas W. W., Sánchez-Guzmán R. A. & Vargas-Medina E. "Experimental Analysis of the Random Me mory Space".IEEE lnternational Conferen ce on Neural Networks. IEEE World Con gress on Computational lntelligence . Vol. 1. 1994.
3. Graham, R. L., Leeb, K. And Rothschild,
B.L. "Ramsey's Theorem far a Class of Ca tegor ies·. Adv. Math., 1972.
4. Graham, R. L.. Rothschile, B. L. & Spencer.
J. H. "Ramsey Theory". USA. John Wiley and Sons !ne. 1990.
5. Hales.A .W. and Jewett, R. l. "Regularity and Positional Games". Transactions American Mathematical Society. 1963.
6. Radziszowski, Stanislaw P. "Small Ramsey
Numbers''. Electronic Journat of Combina torics. 2000.
7. Ramsey, F. P. "On a Problem of Formal Lo
gic". Proc. London Mathematicla Society.
1930.
8. Schur, l. "Uber die Kongruenz xm + ym zm (mod p)". Jber. Deutsch. Math. Verein. 1916.
9. Rada. R. "Verallgemeinerung Eines Satzes von van der Waerden mit Anwendungen auf ein Problem der Zah1entheorie". Sonder ausg. Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Klasse.. 1993.
10. Stern, August. "Matrix Logic". Elsevier Sci
ence
Publishers
B.V.
1988.
11. Villanueva-Rosales N. & Figueroa-Nazuno
J. "Superposición de Información en la Me moria Aleatoria". XL Congreso Nacional de Física. Monterrey, N.L., México, 27-31 de
octubre, 1997.
12. Van der Waerden, B. L. ºBeweis einer
Baudetschen Vermutung". Nieuw Arch. Wisk. 1927.
13. Milburn, G. J. "Schródinger machines: the quantum technology reshaping everyday life". W H. Freeman & Company. 1997.
![]()
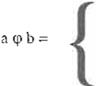 O si nRb
O si nRb

 Resultados
pa
1
a
mAtnces
de
tamann
120x
J
2U
r.:on 16 tre11sformac1ones
Resultados
pa
1
a
mAtnces
de
tamann
120x
J
2U
r.:on 16 tre11sformac1ones
 Resultados
par:? ma 1íces
de
tameño
30Ux300
con
16
tra •s1ormac1onFs
Resultados
par:? ma 1íces
de
tameño
30Ux300
con
16
tra •s1ormac1onFs
 b)
b)

 1.,, • , • Tabla 5.
1.,, • , • Tabla 5.