Una propuesta para la evaluación de opciones financieras: La Fórmula de Primer Acercamiento
Act Adolfo Marlinez Huerta
Universidad La Salle
E·mali
.
<:1mart111h@banamex
com>
RESUMEN
Rec1b1do; Septiembre de 2001 Acepl'l '"' , . ¿vlernb <: (IJ; 2V. 1
Para coadyuvar a determinados estudiantes y participantes de derivados financieros de nuestro país, en el entendimiento de las principales fórmulas de
valuación de opciones como la Black - Scholes o la Bino mial, se presenta una fórmula de valuación, llamada de Primer Acercamiento, para cuya
deducción se utilizan conocimientos básicos en finanzas y que bajo determinadas condiciones esta fórmula se puede considerar como un caso particular de
la Fórmula Binomial.
P
a
l
a
bra
s
claves: valuación, opciones. Fórmula de Primer A
ce
r
camie
n
to, Fórmu
l
a
B
i
nom
i
a
l
.
ABS1RACT
In order to help sorne Mexican students and participants of financia! derivatives to understand the main option valuation formulas, such as Black -
Scholes and Binomial, this work presents a valuation formula named "Primer Acercamiento'' (First Approach). Basic financia! knowledge is used for the
deduction of this formula and under certaín circums1ances it is a particular case of Binomial Formula.
Keywords:
valuation, options, F1rst Approach Formula,
Binomial Formul
a.
1. INTRODUCCIÓN temática empleada es superior a la que mane· jan , lo que en ocasiones provoca que díchas
El mercado de derivados en México está en su
inicio. su pnncipal objetivo radica en el manejo del riesgo financiero de una empresa o de una persona. Entre estos instrumentos, se espera que las
opciones tengan un lugar especial por su gran versatilídad.
Con el fin de obtener el máximo beneficio de las opciones, es indispensable realizar una valuación de los mismos. Ésta puede realizarse
fórmulas se utílícen como una "caja negra". es decir, se toma el resultado como "dado". sin mayores cuestíonamientos (aunque en oca· siones con
reservas),sobre todo por la existen cia de una gran cantidad de paquetes de computación; sin embargo,esto puede inhibir su deseo de conocer los
principios de la valuación de las opciones .1
a través de varias fórmulas . entre la s que desta can la de Black & Scholes. cuyos autores, por
su excelente trabajo se hicieron merecedores del Premio Nobel de Economía 1997, y la Bino mial.
El problema con estas fórmulas, para algunos estudiantes y participantes en el medio fi nanciero de nuestro país, radica en que la ma·
1 Aquí el punto es que algún estudiante, con cierto poten
cial. ouede dec1d1r que la matemática utilizada en la valuac1on de opciones es tan comple¡a (ecuaciones dife· renciales. proceso de Wrener. límites.
etc.). qi,;e 10 desa liente a conocer más, lo que para la cultura financiera - matemática de los estudranles y par11c1pantes de nueslro país serla
unalnsteza,desde luego queda el punto de la
motivación.pero sies posible hacer un aceccamiento más amable,elsuscrito no ve porqué no hacerlo
0'1 Cont /1 v (M x) Vol 5 Num 19 Juk?r 2002 33
Por lo anterior. el principal objetivo de este artículo, es mostrar cómo deducir una fórmula para valuar una opción Cal/ cuyo subyacente sea
una acción, al que se le denominará de Pri mer Acercamienlo,2 que es sumamente accesi ble (y hasta cierto punto obvia) para la mayoría de los
estudiantes, particularmente de finanzas. de nuestro país y a partir de ella mostrar como se puede relacionar con las fórmulas avanzadas de valuación
de opciones antes comentadas. La idea es que se pueda comprender3 satisfactoria mente lo que es una fórmula de valuación de opciones.
Para el buen entendimiento de este artículo, es necesario que el lector tenga conocimientos básicos de las opciones,4 así como de matemá ticas
financieras (incluyendo la tasa de rendi miento continua), de álgebra elemental, de esta dística descriptiva y del mercado de valores.

2 La primera versión de la deducción de esta fórmula, a la que originalmente se le llamó "Fórmula discreta para va luar Warrants". la publicó el
suscrito en el periódico El Economista. suplemento Fondos de Inversión, sep. 98. pp 23-24, y posteriormente se hizo una reproducción del mismo
en el Bolelin lnformalívo de la Asociación Mexr cana de Analistas Técnicos, nov 98, pp 6-16. En esa ocasión se le hizo notar al suscrito que,
la Fórmula Brno mial, y muchas otras más, también son discretas, por lo que el nombre original generaba confusión y se cambió al de Fórmula de Pnmer
Acercamiento. Ademas había que aclarar ciertos detalles en la deducc1on, los que se espera queden solventados en el presente articulo.
3 Puede decirse que se entenderá una fórmula. cuando al modificarsele algunos parámetros pueda deducirse (pronosticar) el cambio que se dará en e1
resultado de la misma, esto contrasta con el hecho de modificar el pará· metro, ver el resultado y después tratar de deduclí qué pasó. hecllo que
acontecería si se uhllza la;órmufa en un paquete de computación (se dan las entradas y se dan salidas). Un ejemplo interesante y fácilmente comproba
ble, es pedir a un participante que explique por qué al aumentar la tasa de rendimiento libre de nesgo, aumenta el valor de la opción, cuando en
principio fa lógica financiera dina que debe ba¡ar
• Sobre todo en lo referente a su definición, su operación y a los factores que la aectan Es importante hacer notar que en México, a la fecha,
solamente se opera de manera for mal, una modalidad de opción, que se conoce con el nom bre de titulo opcional o warrant. Desde luego, los
resulta dos de este artículo también se aplican a dichos Htulos. Una propuesta de valuación del precio de un tltulo opcional se publrcó en esta misma
revista: Pérez Ellzalde y Gómez Ramírez, E., "Estimación del precio de un titulo opcional mediante una red neuronal art1f1c1al", Rev Cenlro lnv (Méx), vol. 3, núm 12, pp. 419-437, enero-junio de 1999,
34
En el artículo se supone que las opciones son europeas, que el subyacente es una acción que no reparte dividendos y que no existen costos de
transacción.
2 La Fórmula d Prln.er .l.\t::Brcam1e:1ito (FPA¡
Un estudiante de opciones se puede dar una idea de la valuación de una opción Cal/ , y la manera en que la afectan ciertas variables.
en particular el precio del bien subyacente, si sigue la forma de razonar de un inversionista en op ciones a vencimiento, que las utiliza únicamente
para fines de especulación5 y cuya comparación sea con una inversión libre de riesgo, como puedan serlo los cetes.
Así un inversionista puede 1nvert1r a un plazo de t días una cantidad C en celes, cuya tasa de rendimiento sea i, o bien puede invertir esa mis ma
cantidad C en una opción Cal/ a vencimien to.
En caso de que invierta en celes. su monto a vencimiento es:
e (1 + iU360)
(Ec 1)
Por lo tanto, lo que buscará el inversionista es que su inversión en una opción sea superior a esta cantidad, o para fines académicos, pode mos decir
que sea igual a dicha cantidad.·
Si definimos a S como el precio de la acción a la fecha de inicio y a k como el incremento por centual del precio de la acción a vencimiento, se
deduce que el precio a vencimiento de la acción será:
s (1+ k)
(Ec
2)
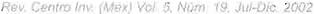 Es decir, la opción puede utíl1z.arse como cobertura y como especulación. a mayor/a de los libros de opciones, y el presente artlculo. utihzan este
ult:mo acercamiento para evitar 1ntroduc1r "ruido" en la deducción; sin err.bargo, al 1í avanzando en el conoc1m1ento de las opciones, al gunos
lecores pueden llegar a confundirse (ahondar so bre esto esta fuera de los lírn1tes de este a1iículo).
Es decir, la opción puede utíl1z.arse como cobertura y como especulación. a mayor/a de los libros de opciones, y el presente artlculo. utihzan este
ult:mo acercamiento para evitar 1ntroduc1r "ruido" en la deducción; sin err.bargo, al 1í avanzando en el conoc1m1ento de las opciones, al gunos
lecores pueden llegar a confundirse (ahondar so bre esto esta fuera de los lírn1tes de este a1iículo).
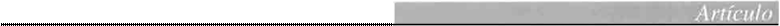
La ganancia de una opción Call europea a vencimiento es su valor intrínseco, que por defi nición será el valor mayor entre su precio a
vencimiento menos su precio de ejercicio X y cero, es decir:
Max ( S(1+k) - X , O )
<E
,
3)
Por el momento, si sólo se toman en cuenta los valores positivos, el valor intrínseco seria:
S ( 1 + k) - X
en dónde S y X se definen como antes, r es la tasa libre de riesgo de manera continua y, que para estos efectos, se define r = In (1+i), T es el plazo
a vencimiento como fracción de un año, N(d) = resultado de aplicar a "d" la distribución normal acumulada y v es la volatilidad del bien
subyac ente.
Y, en consecuencia, ambas fórmulas,tanto la Black-Scholes como la FPA, pueden represen tarse de forma general6 como.
C = Su-XB
(Et:,
4)
Entonces, para que estén en equilibrio esta cantidad debe ser igual a la obtenida en cetes, es decir:
C (1+ iV360) = S(1+k) - X
(/
=
5)
Despejando a C, tenemos la Fórmula de Pri mer Acercamiento (FPA):
S(1+k) - X
e = (1=it/360)
í
E
c
6)
Para efectos académicos es conveniente pre sentar la FPA de la siguiente forma:
|
|
(1+k)
|
|
1
|
|
e = s
|
(1+iV360)
|
- X
|
(1+it/360)
|

 rEi- í'J
rEi- í'J
La razón de esto es porque la Fórmula de Black-Scholes es la siguiente:
C = S N(d1) - X e·rT N(d2)
t
E
c
9)
Expresado de otra forma. el valor de una opción Ca//, es la diferencia del precio actual del precio ponderado por un factor o. menos el pre
cio de ejercicio ponderado por un factor -
Estos factores. dados para la Fórmula de Black-Scholes están en función del plazo a vencimiento, la tasa de rendimiento continua libre de riesgo y la
volatilidad del precio de la acción.
En el caso de la FPA, los factores están en función del plazo a vencimiento. la tasa de ren d1m1ento libre de riesgo y el incremento a ven
cimiento del precio de la acción.
Por ejemplo, sea S = X = 35 30, t = 178 días, en cuyo caso T = 178/360 = O 49, i = 17.33%, en cuyo caso r = ln(1+0.1733) = 15.98%,
sea k =
16.95% y V :: 0.43
Entonces para la FPA tenemos que:
(1+0.1695)
 e =
35.30 (1+0.1733•178/360)
e =
35.30 (1+0.1733•178/360)
Definiéndose:
(Et 8)
- 35.30 1
(1+O 1733* 178/360 = 5.51
ln(S/X) + (r + v2/2)T
d1= v .JT y d2 = d 1 - V v'T
6 El suscrito ha v1slo vanos libros que utrlizan esta represen tac1órl sinlélica de una fórmula para valuar opciones Cal/.
la de este an1culo es una versión modificada de la que
aparece en el libro de Brown y Kritzman {ed). Quantitc;tive
Methods for
F
inancia/ Analys1s
,
Edrtonal CFA, 2ª. edición,
1989
Y, para la Fórmula Black-Scholes tenemos que:
ln(35.30/35.30)+(0.1598 + 0.432/2)0.49
d 1= v0.43 v0.49 =0.41
d2= 0.41 - 0.43 '10.49 = o 11
Como punto de partida tomemos una forma usual de razonar, que consiste en que en vez de tener un escenario. se pueden dar tres: el pesi mista, el más
medio y el optimista.
Cada estado de la naturaleza puede valuarse en forma independiente con la FPA, en cuyo caso tendríamos 3 valores de C, a los que pode mos denominar
como C1, C2 y C3• es decir, cada
C= 35.30 N(0.41)-35.30 e-0 1598
N(0.11)=5.51
Ch (para h=1,2,3) consistirá en el valor de una opción para cada uno de los escenarios comen tados.
Desde luego, en este caso se buscó que la k,
esto es el incremento esperado en el precio de la acción a vencimiento, fuera el correspondien te a una volatilidad de 0.43 en el precio de la acción,
razón por la cual producen el mismo resultado.
Es importante hacer notar que la FPA en sí está manejando un único escenario o estado de naturaleza, que se representa por k, razón por la que también
puede llamarse Fórmula de Pri mer Acercamiento Puntual; sin embargo. puede extenderse y bajo ciertas condiciones puede in ducirse a la Fórmula
Binomial, lo que se verá en la siguiente sección.
Además, tal como está presentada la FPA puede no ser consistente con la Cal/-Put parity, por lo que de emplearse
equivocadamente se es susceptible a ser arbitrado.
Como se ha comentado. el objetivo de la FPA es coadyuvar a determinados estudiantes e in teresados en el tema, al entendimiento de las fórmulas de
valuación más avanzadas y de ninguna manera las pretende sustituir.
Con estos tres valores puede obtenerse un promedio ponderado por la probabilidad de ocurrencia de los mismos. a lo que se le deno mina el criterio del Valor Medio Esperado (VME).7
Lo anterior se expresa algebráicamente como sigue:
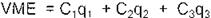
(Ec
.
10)
donde las Ch (para h= 1,2,3) son el valor de la opción determinados por la FPA (Ec. 6) para un escenario en particular, y las qh (para h=1,2.3) son la
probabilidad de que ocurra ese escena rio, por esta condición, se necesita que:
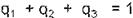
(Ec 11
)
'.) L...1.
f HiT11 da d'=- Primer Aci-.::rr,arrnento y la FN
n 11la B1namk1I
Está claro que un único estado de la naturaleza, esto es, un único precio a vencimiento de la acción es una visión limitada para valuar un op ción Cal/ , de ahí que el siguiente paso sea bus car cómo extender los alcances de la FPA. Para efectos de este artículo únicamente se mostrará un
camino que, partiendo de la FPA, nos permi ta llegar al caso particular de una fórmula más avanzada: la Fórmula Binomial de Dos Pasos (Two-Step Binomial Tree). por lo que no es una demostración formal.
7
A este promedio. dentro de la Teoria de la Dec1s16n, se le conoce con este nombre, pero dentro de la probabilidad y ta estadística, se le conoce
com<> la Esperanza de una Variable Aleatoria, o primer momento alrededor del origen: así, si a la misma la denotomos como x, entonces se de fine
como:
E(x) ;:: E io:h f(xh)
En el mundo empresarial y financiero lambién se uti112a, y se le suele denominar como er Rend1m1ento Esperado de una Inversión, de igual forma se
emplea en et mundo académico. ain::¡ue con otra on:erpretacíón; así. un profe sor puede decidir que la nota final del curso podrá ser, por eiemplo, el
60% el examen ftnal, el 30% los exámenes paretares y el 10% las tareas.
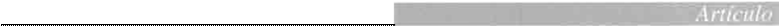
Si sustituimos el valor de las Ch tenemos que:
Se necesita, en todo momento, que los distin tos valores S(1+kh) - X (para h=1.2,3) no sean negat ivos, por lo tanto, si esta condición en la
VME := 8(1-'-k:) - X
--· -··-·-·· -
(1+it/360)
q2 +
q1 + S(1+k2) - X
(1 +iU360} S(1+k3) - X Q3 (1+1t/360)
fórmula se escribe de manera explícita. que daría:
VME=e-rtl36º[Max{($( 1+k1)-X).O}q1+
Max{(S(1+k2)- X),O}q2 + Max(($(1+k3) - X).O}q3]
De lo anterior se aprecia que cada uno de los tres escenarios tiene el mismo valor de ejercicio X. el mismo precio actual del bien subyacente S. la
misma tasa de interés i, el mismo plazo t. y la única diferencia se da en el valor de la k (lo que está representado por las distintas k;). es decir.
lo que cambia es el escenario, en función del incremento porcentual esperado a vencimiento del bien subyacente.
Si se factoriza se tiene que:
VME = (1+it/360)- 1 [(S(1+k1) -X} q1 + ($( 1+k )· X)
Si se define:
fuu = Max{(S(1+k) - X), O}
fud = Max{(S( 1+k2) - X). O}
fdd = Max{(S(1 +k3) - X). O}
Y sustituyéndola se tiene que:
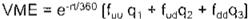
-¡
Si se hace que:
q2 + (S(1+k3) - X) q3)
(Ec
f
J
)
V
360
= 20T
Y se invierte el orden den1ro de los corchetes.
Conoceremos la fórmula anterior con el nom
bre de el Valor Medio Esperado de la Fórmula de Primer Acercamiento (VFPA).
El valor (1 +iU360)-1 corresponde al factor de descuento utilizando una tasa de rendimienlo i. si en vez de utilizar esta tasa se utiliza su equi
valente continua, es decir:
r = ln (1+ i)
Entonces este factor de descuento se trans forma en:
Sustit uyendo este valor en la VFPA, se tiene que la fór mula se convierte en.
entonces :
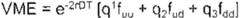
Si se definen las probabilidades de la si guiente manera:
Q1 = p2
Q2 = 2p(1-p)
Q3 = (1-p)2
En donde puede observarse que la suma de las qh (para h=1.2,3) es igual a la unidad. y si
además se sustituye VME por f, finalmente se tiene que:
VME = e-t1!360 ((S(1+k1} - X) q1 + (S(1+k2) - X) q2
+ (S(1+k3) - X) Q3]
(E
14
 J - !(; - ' .-
J - !(; - ' .-
f e·ZrOT (p2
fuu + 2p(1-p)fud + (1-p)2
fctctl

Esta fórmula. es la Fórmula Binomial, corres pondiente a la de Dos Pasos (Two-Step Binomi al Tree). y aparece en la página 202 del
libro de Hull, Options. Futures and Other Oerviates, 3ª. edicróns, se permite señalar que se buscó res petar,en lo posible,la notación
original de dicho autor,y que la p tiene una rnetodologia particu lar de cálculo, que en este artículo no se expli ca.
Es importante hacer notar que el desarrollo original de la Fórmula Binomial la hicieron Cox, Ross y Rubinstein,9 pero se decidió utilizar la versión de
Hull, debido a que es una publicación más reciente, a que tiene un acercamiento más didáctico y, además. porque este libro y esta edición son una de
las cuatro lecturas sugeridas por la Real Academia Sueca de Ciencias,10 cuando dio información relativa al otorgamiento del Premio Nobel de Economía
1997 a los pro fesores Robert C. Merton y Myron S. Scholes, por su contribución en el desarrollo de la fórmu la para valuar opciones. mejor conocida
como Black & Scholes.
4 Una ilustra ion
Para ilustrar las fórmulas anteriores, empleare mos el mismo ejemplo utilizado en libro de
1
Lo anterior significa que 6 meses después, el precio de la acción puede lener solamente 3 va lores:
1) 24 .2, en cuyo caso el valor intrínseco fuu= 3.2
2) 19.8, en cuyo caso el valor intrínseco fud= O.O, y
3) 16.2, cuyo valor intrínseco es fdd=O.O
Con esto se tiene que:
f = e-!º '2l(0 Si((Q.6523}2 (3.2) +
2(0.6523)(0.3477)(0) + (0.3477)2 (O)]
f = 1.2823
Para utilizar la VFPA, requerimos construir los escenarios que esperamos puedan darse a vencimiento, y que para este ejemplo serian el pesimista, el
medio y el optimista y, pcsterior mente,asociarles a cada uno de ellos una pro babilidad.
Tal como está planteada la FPA y en conse cuencia la VFPA, tanto los estados de la natura leza como las probabilidades asociadas se ha cen de
acuerdo con el criterio del tomador de decisiones; sin embargo, esta flexibilidad podría ocasionar algunas inconsistencias (y en un mo
Hull,1
cuando ejemplifica la Fórmula Binomial
mento dado ser arbitrado).
de dos pasos, antes comentada.
Calcularemos el valor de una opción Call re ferida a una acción, el precio de ejercicio es de 21, el plazo de vencimiento es de 6 meses y la
tasa libre de riesgo es de 12% continua anual. El precio de una acción tiene un valor actual de 20, y puede subir, en el primer trimestre, 10% con una
probabilidad de 0.6523 o bajar 10% con una probabilidad de 0.3477, esto se repite para el siguiente trimestre.
& Hull. John C , Optsons, Futures and Other Derivatives.
Prentice Hall, 3'. ed1c1on. 1997.
g Cox, Ross and Rub1nste1n. 'Opti0'1S Pnc1ng A S1mptífied Approach", Journal of F1nanc1al Econom1cs. September 1979, pp 2.29·263.
'º (En línea) Disponible en: http.//www. nobel.se/economics/· laureates/1997/press html. agosto de 2001
11 Hutl, op c11
Por ello, para efectos de esta ilustración bus caremos ser congruentes con la Fórmula Bino mial de dos pasos; en consecuencia, los esce narios
serían: el pesimista cuando el precio de la acción sea de 24.2. lo que significa un incre mento a vencimiento del 21% (con respecto a su precio actual
de 20}, la probabilidad de o currencia asociada a este escenario es de 0.4255; el medio seria cuando el precio de la acción sea de 19.8, que significa
un decremento del 1%, la probabilidad asociada es 0.4536; y el optimista, cuando sea de 16.2, esto es un decremento del 19%, con probabilidad asociada
de 0.1209.12

'?Evidentemente los precios corresponden a los mostrados en la fórmula binomial, en tanto las probabilidades se determinaron así: pes1m1sta
(0.3477)(0.3477) = 0.1209,
probable 2(0.3477)(0.6523) = 0.4536 y optimista
(0.6523)(0 6523) = o 4255
 e 11 1 N 11r1
e 11 1 N 11r1
_ _ - Ai tíéúlo·,

En el cuadro anexo mostraremos gráfica mente la distnbución de probabilidad utilizada. Esto es, decimos que a 180 díAs se espera que el incremento del
precio de la acción sea del 21%, con una probabilidad del 42.55%; de me nos 1% con una probabilidad del 45.36%; y, de menos 19% con una probabilidad
del 12.09% respectivamente.
Con estas consideraciones, el valor de la opción seria el resultado de:
VFPA = [(20(1+0.21) - 21) (0.4255) + (20(1-
0.01) - 21) (0.4536) + (20(1-0. 19) - 21) (0.1209)] ( 1+0.1237*180/360)
Dado que los 2 últimos valores delnumerador son cero (ya que por definición de opción, al vencimiento se toma su valor intrínseco, y éste sólo puede
ser positivo), tenemos que el resul tado es:
VFPA = 1 2823
Desde luego el resultado es el mismo, toda vez que, como se mencionó, se utilizan los mis mos datos para elcomportamiento del precio de la acción, y
la tasa de rendimiento que se em plea es la equivalente a la tasa de rendimiento continua del 12%.
5. Conclusión
Para algunos estudiantes y participantes en el medio financiero. la FPA puede utilizarse para coadyuvar en elentendimiento de fórmulas más avanzadas de
valuación de una opción Cal/, toda vez que puede considerarse como un caso particular de la Fórmula Binomial, y que la de ducción de
la FPA es bastante sencilla.
Además, y toda vez que en límite la Fórmula Binomial se convierte en la Fórmula de Blacl<-Scholes,13 pueden realizarse otros estu dios apoyados en
la FPA, que permitirían el analisis de las opciones con un punto de vista complementario al que se ve en los libros, usualmente empleados en nuestro
pais, para la enseñanza de opciones.
![]()
![]() Es decir, la opción puede utíl1z.arse como cobertura y como especulación. a mayor/a de los libros de opciones, y el presente artlculo. utihzan este
ult:mo acercamiento para evitar 1ntroduc1r "ruido" en la deducción; sin err.bargo, al 1í avanzando en el conoc1m1ento de las opciones, al gunos
lecores pueden llegar a confundirse (ahondar so bre esto esta fuera de los lírn1tes de este a1iículo).
Es decir, la opción puede utíl1z.arse como cobertura y como especulación. a mayor/a de los libros de opciones, y el presente artlculo. utihzan este
ult:mo acercamiento para evitar 1ntroduc1r "ruido" en la deducción; sin err.bargo, al 1í avanzando en el conoc1m1ento de las opciones, al gunos
lecores pueden llegar a confundirse (ahondar so bre esto esta fuera de los lírn1tes de este a1iículo).