![]() A
nfuu
·
A
nfuu
·
Arturo Espinosa Romero
RESUMEN
La utilización de cámaras electrónicas para la captura y procesamiento de imágenes es cada vez más importante en el estudio de la robótica y la visión por computadora. Con el fin de obtener la relación métri ca entre la cámara y la escena a observar, es necesario conocer las caracteristicas fisicas del la cámara. En este artículo se presenta una guia para la estimación de los parámetros internos de cámaras CCD. El método descrito en este trabajo -basado en el trabajo Kanatani- toma en cuenta posibles distorsiones de la imagen producidas por la óptica de la cámara y presenta una caracterización del ruido inherente al dispositivo
Palabras clave: Robótica y visión, cám&ra eco. calibración. instrumentación.
ABSTRAC'T
The importance of the use of electronic cameras for the capture and processing of images in the fields of robotics and computational vision is conhnuously increasing. With the purpose of estimating the metric relationship between the camera and the scene being observed, it is necessary to know the camera's physical characteristics. In this article a guide to the estimation of the interna! parameters of a CCD cam eras is presented. The described method -based on the work of Kanatani- takes in account image distor tions produced by the camera's optics and presents a characterization of the device's inherent noise.
Key words: Robolics & vision, eco camera, calíbratíon, instrumentation.
1 INTRODUCC IÓN es el propuesto por Tsai, que propone un méto do automático en dos etapas para la estimación
Llamamos calibración de cámaras al proceso mediante el cual encontramos los parámetros internos y/o externos de una cámara; los pará metros internos determinan las características geométricas y ópticas de la cámara. los pará metros externos determinan la orientación y posición de la misma con respecto a un marco de coordenadas. Los parámetros internos y externos son independientes entre si.
Este artículo tiene como ob¡etivo hacer una presentación básica de la calibración de cáma ras, en particular en el cómputo de los paráme tros internos de una cámara CCD (Charged eoupled Oevíce). Existen varios métodos para
la calibración de cámaras que han sido pro
puestos en los últimos años: un ejemplo clásico
de los parámetros internos y externos de una cámara.
El método descrito en este artículo esta basa do en el trabajo de Kanatani [3]: aunque el mé todo descrito no es automático es lo suficiente mente simple para poder calibrar la cámara en poco tiempo (una vez que se ha creado el códi go necesario). También tiene la ventaja de que, puesto que se toma en cuenta la incertidumbre inherente del proceso de captura. es posible obtener una estimación de la incertidumbre de los parámetros estimados: el cálculo de la incer tidumbre puede ser de extrema utilidad para ciertas aplicaciones, como la robótica, en donde suele ser necesario definir intervalos de confian za en el movimiento del robot.
Rev C,.;>ntl'O l 11 v i'Méx J Vol. 5 Num 19. .lul D11; :t002 41
![]() A
nfuu
·
A
nfuu
·
El articulo esta organizado como sigue: En la primera sección se describe el modelo de la cá mara, y cuáles son los parámetros internos de la misma. En la segunda sección se describe el método utilizado para eliminar las distorsiones producidas por el lente de la cámara. En la cuar ta sección se introducen algunos conceptos pre liminares de geometría proyectiva que son necesarios para definir el método de calibra ción. En la quinta sección se describe el método utilizado para hallar el centro óptico de la cáma ra, mientras el método utilizado para averiguar la longitud focal es descrito en la sexta sección.
![]()
Los parámetros que definen las características geométricas de la cámara son básicamente la longi ud focal f las coordenadas del centro ópti co de la cámara (X 0.Y0), y la razón entre las
escalas verticales y horizontales de la imagen1 ( k ,. k,.). La relación que describe el modelo de la cámara es descrita mediante la siguiente ecua ción linear:
![]()
sión discreta de la imagen proyectada en el sen sor de la cámara. Como la información acerca de la densidad de pixeles en el sensor no siem pre está disponible, es más conveniente conce bir al parámetro/ como un factor de conversión, cuyas unidades son pixeles en lugar de metros. Esta convención se utilizará en el resto de este artículo.
Las caracteristicas ópticas del modelo de la cámara son descritas como la distorsión pro ducida por el lente de la cámara (distorsión ra dialy tangencial). Como fue indicado por Tsai (5] en la mayoría de las polinomiales industriales de visión automatizada. únicamente se conside ra la distorsión radial.
3 Elln 1na .1 :n ele la d1slorsi6n.
El primer paso en el proceso de calibración es la ehminación de las distorsiones en la imagen producidas por el lente de la cámara. La distor sión es modelada con un par de funciones que mapean el pixel (x. y) en el plano de la imágen
capturado por la cámara (imagen distorsionada)
![]() [X l
[X l
l [0.,, O Xo l[X
a una nueva posición (x.. y ) .
y = z o (),1 ."1.1 :
En nuestro caso, las funciones se definen como las ecuaciones polinomiales:
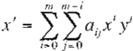
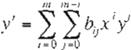 '
Ec
1)
'
Ec
1)
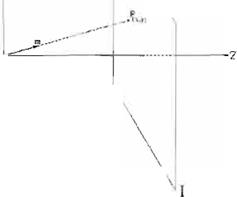
en donde (x,y), es la proyección del punto en la escena P= (X , Y, Z) en el plano de la imagen l (véase la Fig. 1), y los factores escala (o.,.CXi.J.
que combinan la longitud focal y la razón de aspecto de la imagen (ar = k.J.a, = k/> . Se
asume que el lente de la cámara está enfocado al infinito. por lo que la distancia focal represen ta la distancia entre el plano de la imagen y el origen (véase la Fig. 1). Las unidades de la distancia focal son las mismas utilizadas para representar las distancias en el espacio polino miales (e.g. metros) por lo que las unidades de las coordenadas en el plano de la imagen (x.yJ son también representadas en tales unidades. La imagen obtenida con la cámara es una ver-
' Razón de aspecto de la imagen,o -,mage aspect ratio".
42
(E . 2J
en donde m == 2 (x. y) y (/ /J y corresponden a las coordenadas de los puntos en la imagen original y la imagen deseada .
Un número N de coordenadas son obtenidas de ambas imágenes, y al sustituirlas en la Ec. 2 obtenemos un conjunto de ecuaciones lineares con respecto a los coeficientes o,J y b¡.,; resol viendo dichas ecuaciones bajo un criterio de minimos cuadrados (1] se halla una aproxima ción de las funciones que describen el mapeo.
![]() La forma más común de obtener la serie de coordenadas,necesarias en el proceso de elim inación de la distorsión, es utilizar la imagen de una malla
regular de cuadrados tomada con la cámara perfectamente perpendicular a ésta (imagen a) en la F;g. 2). Las esquinas de los
La forma más común de obtener la serie de coordenadas,necesarias en el proceso de elim inación de la distorsión, es utilizar la imagen de una malla
regular de cuadrados tomada con la cámara perfectamente perpendicular a ésta (imagen a) en la F;g. 2). Las esquinas de los
![]()
![]() •,\
•,\
\
\
\
¡,
,X \
'\
" --1>
![]() \ (...,., 1 --"
\ (...,., 1 --"
----1- - --··.
Plano de Ja imácn
|
' ' •. .. f 1 \
--z
(Xo.Yo)
Cen1ro
óp1ico
p f'linlo en la ecena
\y \
\
\
\
(x , y) Proyección d.:; P en el plano de la imágen f
O Ongen del sis1err1>1 de coor
denadas de IR cáimira
j 1
Fig 1 : Pmyo c c 10n nerspp1·tiva de 18: esa:nr:t n, 1 ._,¡ J/ ::1110 1ie Ir. i111agr-:1 1.
cuadrados son usadas como puntos de referen cia; para extraerlos se utiliza un de1ector de bor des Canny (2) (imagen b) en la figura 2), y líneas pueden entonces ser ajustadas a los bordes de cada cuadrado. Las coordenadas de las inter secciones de líneas de cada cuadro se utilizan corno una estimación de las coordenadas de las
esquinas de los cuadrados, o puntos de referen cia . En las imágenes utilizadas en la Fig. 2, cada cuadrado mide 1 cm. por lado, y la distancia entre la camara y la malla es de 13.5 cm. La imagen ideal fue modelada con una malla regu lar compuesta por 280 puntos. misma que fue centrada en la malla obtenida de la imagen ori ginal Las coordenadas de los puntos de la malla original y de la malla ideal fueron substi tuidas en la Ec.2, y el conjunto de parámetros a,1, y bu fueron estimados.
|
I'(x, y ) = r(M/x,y),M}' ( x,y))
En el ejemplo mostrado en la Fig. 2 el tama ño original de la imagen obtenida por la cámara es 640 x 480 pixeles; después del mapeo el tamaño de la imagen fue 672 x 487 .
Es conveniente, al momento de calcular las funciones que definen los mapas. normalizar las mallas real e ideal de puntos. de tal manera que sus valores varien entre - l y 1 , para así evitar problemas de precisión. También se puede ex perimentar con valores pares mayores a 2 para el orden de los polinomios utilizados (m= 4 ó m =
6) en la Ec. 2.
Es también necesario tomar en cuenta que al momento de hacer el mapeo entre la imagen original y la imagen corregida, cierto tipo de in terpolación de los valores de la imagen en cada pixel es necesaria. En las imágenes utilizadas en este articulo se utilizó una interpolación bili near; una muy buena descripción de los posi bles tipos de interpolación que pueden utilizarse puede encontrarse en Milan Sonka (5].
![]()
Esta sección contiene una breve introducción a conceptos basicos de geometría proyectiva y está basada principalmente en el trabajo semi nal de Kanatan1 [3]. que resalta de otros trabajos sobre el tema en los que se toma en cuenta la incertidumbre del proceso de captura, lo cual es muy importante para el trabajo que se hace en visión computacional, en donde no siempre se puede asumir una descripse sensa. Por motivos de espacio. no se incluyen aquí las demostra ciones de lo que en esta sección se afirma,pero
![]() 4J
4J
![]()

|
|
|
![]()
|
![]()
r í J - o r
( .J IJ o o u 1 -1 1
.J L 1 ¡-¡ 1
J · . i n = c 'J
'- '-· l :J ,- o
' _J - o
1 \...
f
u r 1
u
n
e ._ ,
a) o)
 ••••••••••••••••••
••••••••••••••••••
|
|
d) •••••••••e)
F 1g 2: P roceso de el11rnnM 1o n de fa distors1on. la w1agen a) muestra fa 1magn l)lliJinal, b) muestra los
!;01(16 aor emd o s cc11, e! u<A-.jclo1 de bordes Ga111'1. e) ·w13strí:. 12. mal/.::. ong1nc1 ' 'e ow1tos que $e ajusta ¿¡
/as esoi.ú ·:·-: d- h,.. cuadrados "'" la 1r•1ager1 /J J v d) mi.Jt::S(, a /2 1 1 -·,.,en co1reg1da
\
\
.x X
|
|
\
\ y
<I)
r \·-
0\: .--·-·
\y
1 \.t.
![]() \ -
\ -
í_y ---L
\
l b)
![]()
l '? ev C P.ntro /1111 ( 11, X I Vol ) N(1111 1<) f (I / D1<; '> UOI.
![]()
se pueden encontrar a detalle en el texto de Kanatani.
" 1 R epra.:8nt-:i·ór de ¡;un l. s y 1u1eac; P-11 el p!anr de la imagen
Los puntos y líneas en el plano de la imagen J son representados por medio de coordenadas homogéneas, que son definidas como una tri
pleta de números reales m = (m1. m2• m3l . en
donde no todos ellos son iguales a O. La relación entre las coordenadas homogéneas m, de un punto P. en el plano de la imagen y sus coordenadas cartesianas (:i., y ) está dado por
coordenadas (x, y) será representado por elvec tor normalizado
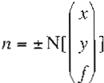
(Ec .5)
mientras la línea que yace en el plano de la ima gen, descrita por Ax + By +C = O. es representa
da por el vector normalizado
X = j
m ' , y :::o f m ,
m ,,. ± N(( ;]]
- - -
m3 m 1
C / f
. 6)
Una línea en el plano de la imagen puede definirse por una tripleta de números reales n = (11 1• nz, n.•?. en donde no todos ellos son iguales
a O; la linea representada por /1 aparecerá en el plano de la imagen. en las coordenadas carte sianas definidas por
![]()
(E 41
Las coordenadas homogéneas del punto P, en el plano de la imagen, pueden ser concebi das como el vector que partiendo del origen O y que apunta hacia el punto P (véase la imagen a) en la Fig. 4). Las coordenadas homogéneas de la linea L, en el plano de la imagen pueden, a su vez:, ser concebido como el vector normal al plano que pasa por el origen O, e intersecta la linea l (véase la imagen b) en la Fig. 4).
Como la relación entre coordenadas homogé neas y su equivalente representación Cartesia na depende únicamente de la orientación del vector, las coordenadas homogéneas pueden ser multiplicadas arbitrariamente por un número diferente a cero, sin perder sus propiedades; con el fin de mantener la magnitud del vector en un rango razonable, la dividimos por su norma. En elresto de este artículo nos referiremos a los puntos y a las lineas en el plano de la imagen,
usando su vector normalizado . De acuerdo a
esto. un punto en el plano de la imagen con
Rev Cvnfro lnv M 1:;1 x Vol 5. N .-., 19 ul·Dt . 2M
en donde f representa la longitud focaly N es el operador de normalización definido como sigue:
u N(u) = -
fu l
r L 7)
A. 2 Mciclel') eslatl1s1ir.1. ua• r uír'c
Cuando la imagen es capturada por la cámara , el ruido inherente del proceso tiene que ser tomado en cuenta, para así poder estimar la confiabilidad de las mediciones utilizadas para estimar los parámetros internos de la cámara (en nuestro caso. puntos y líneas en el plano de la imagen).
El ruido del punto de la imagen P cuyas coor denadas homogéneas están definidas por el vector m se define como la matriz de covarianza Vfm] con las siguientes propiedades:
• Es simétrica y positiva semi-definida.
• Es singular con respecto al vector
111 : V{m]m = O
• Su descomposición espectral está definida
por
![]()
o 8)
4 5
![]()
donde <J 1 • <J 2
y O, ( <J , a
>O) son los tres
De la misma manera el vector n de la linea l
2 2 1 2
eigenvalores de V[m} y {u, v m} son los eigen vectores correspondientes.
El RMS de la proyección ortogonal del ruido toma su máximo en la orientación del vector y el mínimo en la orientación del vector
La magnitud RMS del ruido es
![]() .Jtr(V(m]) = Ja; +a;
.Jtr(V(m]) = Ja; +a;
|
que une los puntos P y P' representados por los
vectores /11 y m' está dado por
n = N[m x m' ]
![]()
Cuando tenemos un conjunto de tres o más puntos, decimos que son colineares si hay una linea pasando a través de todos ellos: cuando tenemos un conjunto de tres o más líneas. deci mos que son concurrentes si todas ellas com parten el mismo punto de intersección. Formal mente decimos que un conjunto de puntos son colineares si el rango de su conjunto de vecto res es menor a tres, y un conjunto de líneas es concurrente si el rango de su conjunto de vecto res es menor a tres. El problema con esta defini ción es que es sumamente sensitiva al ruido; unas definiciones más robustas de concurrencia y de colinearidad son como sigue:
V[m.] =
e / ¡-2
2 (ui/ +
VVT
2
Un conjunto de N puntos en el plano de la
magen Pª con coordenadas homogéneas mt;/)
i
.2 2
donde
2(1 + r I f ) 1+ r I f ·
(E . 9)
a=J .. · N son colineares s1 el eigenvalor mas
pequeño de su matriz de momentos
|
"=1

|
r 2
V = ±U X Jn
( t.<.. '1 I )¡
en donde e representa la magnitud RMS del error, que en nuestro caso definimos como 1.
.1 .J Co.111eand ':! ·:i'O- pun,c . y concurr nc1 de
llney s
El vector m del punto de intersección P de dos líneas en el plano de la imagen I y l' represen tados por los vectores 11 y n ' respectivamente está dado por
m = N [ n x n' ]
(b 11)
( C r 1 . 1 )
donde Wua son constantes positivas, es igual a cero; el eigenvector asociado 11 es el vector de
la línea la. que pasa a través de Pa· De la mis
ma manera, un conjunto de lineas en el plano de la imagen l& con coordenadas homogéneas mw o:=J ···N , son concurrentes si el eigenvector mas pequeño de la matriz de momentos
|
N W n n T
No a u
a=I
1 .
donde W,va son constantes positivas, es igual a cero; el eigenvector asoc iado m es el vector del punto P que es la intersección común de las
líneas la .
Los conjunto de constantes W'.11a yW,"'ª son pesos que deben ser elegidos de tal manera
![]() N
.
1
' 00
N
.
1
' 00
![]()
![]()
que a datos confiables les correspondan pesos grandes mientras a datos no confiables se les asignen pesos pequeños. Los pesos óptimos en el sentido de máxima verosimilitud para las Ec. 13 y 14 estan definidos respectivamente por:
ra análoga. la matriz de covarianza de la estima ción óptima del vector 11., de la línea común entre N puntos colineares, esta definida por
UU 7 VVT
w = --1 -
V[n) = -+-
-
Mu n. (Vlmu Jn)
( Ec. 1tia )
A,, )1,v
¡Ec 18 )
![]() "'n
= m ·(V[n,.. lm)
"'n
= m ·(V[n,.. lm)
¡Ec . 1!.if)j
donde {n, u, v} es el sistema de eigenvectores de la matriz óptima de momentos. con los co rrespondientes eigenvalores {0,A.,.,"".}.
4 4 P1mtos en l')I ir fmi!o
El punto en el infinito de una línea en el espacio
Como el cómputo de los pesos óptimos involucra el uso del vector m o 11 que queremos avenguar, se utilizan las siguientes aproxima ciones
es definido como el límite de la proyección de un punto que se mueve a lo largo de dicha linea; si situamos a una línea en el origen de la cámara O, el punto en el infinito de tal linea está dado por la intersección de dicha línea con el plano de la imagen. De esta interpretación, se des
![]() WM(t
=
WM(t
=
t r ace ( V [m "' ] )
( - foa)
prende que, las líneas paralelas en el espacio, cuando se proyectan en el plano de la imagen, se intersectarán en un punto común en el infini to.
|
No. 1race(V [ n , , 1)
f Ec .6bJ
5 E'3trm.c1on delcentro :p·1co.
El centro óptico de la camara. o centro de la imagen, es calculado encontrando el foco de ex pansión (FDE) de un conjunto de puntos espa
Una vez que hemos definido la estimación ópti
ma de la línea formada de un conjunto de pun tos colineares, o un punto como la intersección de lineas concurrentes, es necesario considerar que el ruido de cada uno de los puntos que for man la línea, o de cada una de las líneas que intersectan un punto se propagará en la nueva
línea o en el nuevo punto. Por eso, definimos la
matriz de covarianza de la estimación óptima del vector m, que representa el punto de inter sección de N líneas concurrentes como
ciales de referencia, mientras la cámara es trasladada a lo largo de su eje óptico. El FDE se define como el punto en el infinito de las tra yectorias de los puntos que se mueven en la escena; si movemos la cámara a lo largo del eje óptico, las trayectorias de los puntos de referen cia serán paralelas al eje, y por lo tanto intersec tarán al plano de la imagen en el centro óptico.
El procedimiento para estimar el centro óptico será descrito a continuación:
• La cámara se monta en un "photographic co py stand·'. el cual nos permite controlar la dis tancia ente la cámara y el objeto que se va a capturar. La cámara se monta apuntando hacia abajo, con su eje principal paralelo al eje de movimiento. Un,, malla de cuadrados
donde {m, u, v} es el sistema de eigenvectores
de la matriz de momentos óptima, con los co
rrespondientes eigenvalores {O),,,A,.}. De mane-
P.ov C ::rHIO /111 fJ X) . 1 .• f lum 1.. .1J-D1c 2iJ'J
similar a la utilizada para el proceso de elimi nación de la distorsión óptica se usa como re ferencia. Se captura una secuencia de N imá-
genes, cada imagen se toma con la cámara situada a diferentes distancias de la malla de calibración, y el proceso de eliminación de la distorsión descrito anteriormente, se aplica a cada una de ellas.
Un número M de esquinas de la malla de cali bración se eligen como puntos de referencia. Las coordenadas de cada punto en el plano de la imagen se obtienen de una manera si milar al utilizado en el proceso de eliminación de la distorsión; ésto es. ajustando lineas a los bordes de los cuadros en la malla y, to mando la intersección de las lineas, como los puntos de referencia.
• M Lineas se ajustan a los M conjuntos de N puntos colineares. que fueron obtenidos de las coordenadas de cada esquina registrada en la secuencia de imágenes. La correspon diente matriz de covarianza de cada linea se calcula usando el método descrito en la sec ción 4.3 ( Ec. 13 y 14).
• Se calcula el punto de concurrencia de las lineas y su matriz de covarianza utilizando el método descrito en la sección 4.3 ( Ec.13 y 14).
'5 é.s\1mai.;1on d IGi lonoitud focal
Utilizamos el concepto de "conjugacy" para esti mar la longitud focal. Decimos que dos puntos P y P' con coordenadas homogéneas m y m' se conjugan entre ellos si y sólo si
m · m' = O
(Ec 19)
En otras palabras. dos puntos en el plano de la imagen se conjugan entre sí. si sus vectores correspondientes son mutuamente ortogonales. Podemos definir conjugación en términos de coordenadas cartesianas substituyendo la Ec. 3 en la Ec. 19; con ello podemos afirmar lo si guiente: dos puntos en el plano de la imagen, con coordenadas cartesianas ( a,b ) y (a', b') se conjugan entre si. si y sólo si
ªª , + hb' + ¡1 = o
(t: . 21))
De la definicíón de punto en el infinito y el concepto de conjugación podemos deducir lo si guiente: dos lineas espacíales son ortogonales
entre sí, si y sólo si sus puntos en el infinito son conjugados entre si en el plano de la imagen.
El procedimiento utilizado para estimar la lon gitud focal involucra la estimación de los puntos en el infinito con coordenadas homogéneas m y m' de dos líneas espaciales ortogonales proyec tadas en el plano de la imagen. Como los pun tos en el infinito no necesariamente caen en la imagen capturada por el sensor de la cámara . la mejor manera de representarlos es utilizando sus vectores normalizados. Corno coordenadas homogéneas normalizadas no proveen una ex presión explicíta para su equivalente en el plano de la imagen (si no conocemos el valor de la longitud focal), no podemos utilizar directa mente la Ec. 20. En lugar de eso expresamos la conjugación en términos de la razón de cambio del vector normalízado m al variar la longitud focal del sistema. De la definición de vector nor maliz.ado ( Ec. 5) obtenemos la siguiente expre sión: si m es el vector que representa un punto
en la imagen con respecto a la longitud focal f.
el punto m' representando el mismo punto con respecto a la distancia focalf' está dado por
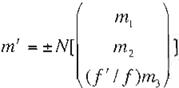
(E.:, 21)
Sustituyendo la Ec. 21 en la Ec. 20 obtene mos la siguiente expresión
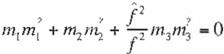
( -f" - ?)
donde m y m ' son los vectores de los puntos en el infinito de dos líneas en el espacio mutua
mente ortogonales, definidas con respecto a una longitud focal tentativa f , mientras 1es la verdadera longitud focal. De aquí se obtiene que la verdadera longitud focal se puede deter minar usando la siguiente ecuación
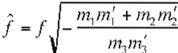
(Ec 23)
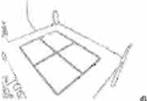
El par de puntos en el infinito conjugados puede ser encontrado por medio de la imagen de una superficie rectangular situada en la escena (véase la Fig. 4). El punto en el infinito VP es determinado como la intersección de las
lineas que pasan a través de los segmentos AB y DC , y el punto en el infinito VP' es deter minado como la intersección de las líneas que pasan a través de los segmentos DC y BC.
Como los puntos en el infinito VP y VP' con coordenadas homogéneas m y m' son calcula dos a partir de una imagen real, una cierta canti dad de ruido, descrita por las respectivas matri
ces de covarianza V[m] y V[m'] deben ser con sideradas. La varianza de la estimación de la distancia focal está dada por
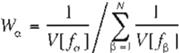
![]()
y la variancia del estimado óptimo de la longitud focal está dada por
V [ j ] = ( 1 V['.fa ]
t E 7)
De la variancia calculada de la estimación óptima de la longitud focal se puede calcular a un intervalo de confianza. La estadística
f - j )Jv [ j ] donde f es la verdadera longitud
|
m' -(V [mJm') + rr: ·(V[m'}m)
focal, obedece a la distribución normalestándar.
100 - a)% puede ser
4 (m1n )
_..; _ 24)
Un intervalo de confianza (
![]() definido como
definido como
La confiabilidad de la estimación de la longi tud focal también depende de la configuración espacia l de las líneas espaciales usadas para determinar los puntos en el infinito; la precisión de la estimación es degradada si los puntos en el infinito encontrados están lejos del centro de la imagen, pero como por definición ellos son conjugados entre sí, hay un número limitado de configuraciones que les permitiera a ambos estar relativamente cerca del centro de la ima gen. En lugar de hallar la configuración ideal para poder determinar la longitud focal. la pode mos estimar como el promedio ponderado sobre N mediciones obtenidas de imágenes diferen tes, en donde se prueban distintas configura
ciones. La longitud focal óptima estimada f se
define como
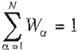
|
u•l
(Ec 25 )
donde fa, o: = 1 . ...,N son los estimados de la longitud focal sobre N imágenes diferentes.
Los pesos se definen en términos de la va rianc1a de las estimaciones independientes de
la longitud focal V{/] como
Re:: ':on r< lm (M x) Vol 5 Nurr1 1g Jul-01c 200.l
( E 281
donde A.a es el punto a% en la distribución normal estándar.
7 Procedrmiento para l(l estimaciór <.i · la 1 r gi tud focal
El procedimiento para estimar la longitud focal se resume en las siguientes líneas:
• Se capturan N imágenes del marco de cali bración con configuraciones espaciales dife rentes, y la distorsión óptica producida por el lente se elimina.
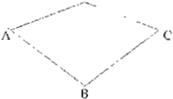
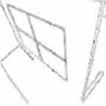
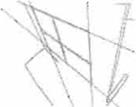
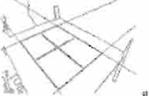
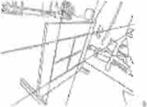
• Los bordes del marco de calibración se ex traen utilizando un detector de bordes Canny (véanse imágenes d)-f) en la Fig. 5).
• Las líneas se ajustan a los bordes del marco de calibración y sus matrices de covarianza se estiman utilizando el método descrito en la sección (ecuaciones 13, 15a, 15b y 18).
• Los puntos en el infinito y sus respectivas ma trices de covarianza e estiman utilizando las ecuaciones (véanse imágenes g)-i) en la Fig. 5).
• La longitud focal se estima utilizando el méto do descrito en la sección 6.

 ..
..
• '·


REFERENCIAS
1. Richard L. Surden y J Douglas Faires Análi sis Numérico, Grupo Editorial Iberoamerica na, 1985.
2. J. F. Canny. A computational approach to edge detection, IEEE Transactions on Pat tern Analysis and Machine fntel/igence, 8(6):679-698, Noviembre 1986.
3. Kenichi Kanatani. Geometric Computation for Machíne Visionn, Núm. 37, en Oxford
Engineering Sciences Series. Oxford Science Publications. 1993.
4. . Milan Sonka. Vaclaw Hlavac, y Roger Boyle. Jmage Processing, Analysis and Machine Vision. Chapman & Hall, 1993.
Roger Y Tsai. A versattle camera calibration technique for high-accuracy 30 machine vi síon metrology using off-the-shelf tv cameras and lenses,
IEEE Journal of Robotícs and Automatíon,RA-3(4):323-344, August 1987