Introducción
Es importante enfatizar que ante el desconocimiento de la dinámica de un nuevo virus la primera herramienta efectiva, conocida desde la antigüedad, para su control, es el aislamiento de la población, ya que el primer problema a enfrentar es la velocidad de contagio, esto es, la velocidad con la que se propaga el nuevo virus. Para el cálculo de esta velocidad de dispersión son necesarias al menos dos condiciones, la primera es que la población sea constante y la segunda que se controle o no exista la posibilidad de re-infección, lo cual se logra separando a la población infectada si es que no existe la inmunidad, que es el caso del virus SARS-CoV-2. A finales del año 2019 surge este nuevo virus SARS-CoV-2 en la ciudad de Wuhan, en China, donde se observó que éste se dispersa con una velocidad superior a otros virus conocidos, esta velocidad de contagio está relacionada con la tasa de transmisión. Ahora, como ya se mencionó, uno de los principales problemas que se presentan cuando surge un nuevo virus es precisamente el cálculo de la tasa de transmisión, ya que para obtenerlo se necesita un control estricto sobre la movilidad de la población, lo que es difícil de conseguir en una ciudad relativamente grande, ya que todo el tiempo hay flujo de personas que salen y entran a la ciudad. Hasta ahora en la literatura (Godio et al, 2020) y (Lin et al, 2020) han reportado un intervalo del parámetro de contagio del virus SARS-CoV-2 de 0.59 a 1.68, dependiendo del grado y tipo de interacción que hay entre la población y del tamaño de la población. Para visualizar la situación, el virus de la influenza H1N1 tiene un intervalo para el parámetro de contagio reportado (Gómez, 2021) de 0.0017 a 0.0021, el cual comparado con el del SAR-CoV2 es notoriamente más pequeño. Otro problema que presenta este nuevo virus es que hay un porcentaje alto de la población que carece síntomas, haciendo que las autoridades sanitarias queden prácticamente ciegas al no poder registrarlas, además de que las personas asintomáticas fungen como vectores transmisores, haciendo que la velocidad de propagación sea más grande al calculado por el registro de los datos. Lo anterior hizo que los primeros brotes del Covid-19 fueran rápidos y que las rutas de contagio se perdieran o no se pudieran determinar en muchos casos (Johansson et al 2020). Las pruebas revelan que un porcentaje alto de personas contagiadas son asintomáticos, lo que provoca que no acudan a los hospitales a hacerse las pruebas correspondientes, a pesar de haber estado en una situación de riesgo. En el contexto anterior y sin contar con un número suficiente de pruebas las autoridades sanitarias tienen que hacer sus proyecciones, en la mayoría de los casos, sólo con el registro de las personas sintomáticas graves y de los fallecidos, lo que conduce a subestimar el número de contagios, ya que la tasa de infección encontrada en estas condiciones está por debajo del valor real, esto debido a que la infección que se propaga de manera silenciosa por medio de las personas asintomáticas. Las principales estrategias que se han implementado para atacar este problema son: 1) proponer un modelo SIR dependiente del tiempo, 2) el uso de estadística inferencial y 3) el empleo de derivadas fraccionarias dentro del modelo SIR.
El presente trabajo utiliza el éxito del modelo SIR, ya que además de que en el caso del crucero Diamond Princess se presentan las condiciones óptimas para su aplicación, este modelo se ha empleado para simular diferentes epidemias como la viruela, el ébola, el sarampión y la gripe en poblaciones relativamente pequeñas (Lennette et al, 2009), pero además se hizo la simulación numérica de los primeros brotes de Covid-19 en la ciudad de Wuhan en China con varios escenarios propuestos (De Castro, 2020). En este trabajo entonces se usa del modelo SIR para simular el brote de Covid-19 en el crucero Diamond Princess por tratarse de un sistema cerrado y por descartar la re-infección, ya que las autoridades sanitarias manejaron el retiro de las personas una vez que fueron infectadas, con lo que se visualiza la dinámica de la dispersión del virus en un sistema cerrado. Los primeros resultados sobre el comportamiento de la pandemia por Covid-19 carecían de la información precisa para una correcta predicción, ya que los principales parámetros del modelo se obtuvieron de sistemas abiertos, los cuales presentan una gran cantidad de variables que influyen en el entorno en el que se desarrolla la infección. Así que, el estudio de un caso controlado proporciona información fundamental sobre la velocidad de propagación del virus. Se tiene registrado (Pengcheng et al 2020) que las características de espacio y de convivencia que se presentan en un crucero hacen que la mayoría de las infecciones respiratorias se produzcan de humano a humano. El Diamond Princess es un crucero de gran lujo que permite que la interacción entre pasajeros y tripulantes sea medianamente homogénea, por lo que el entorno para el contagio es favorable. En base a este conjunto de condiciones el presente trabajo propone que es factible implementar el teorema de umbral de epidemiología (modelo SIR) para el cálculo de la tasa de propagación y el uso del teorema total de probabilidad para inferir el número de asintomáticos.
1. Metodología
Comencemos por describir las condiciones que se presentaron en el crucero, así como una línea de tiempo de su recorrido. El Diamond Princess tiene una capacidad para albergar 3711 personas (2666 pasajeros y 1045 tripulantes). El crucero zarpó el 20 de enero del año 2020 del puerto de Yokohama Japón haciendo el siguiente recorrido durante 16 días: Hong Kong, China, enero 25; Puerto de Chan May, Vietnam, enero 27; Cai Lan, Vietnam, enero 28; Keelung, Taiwan, enero 31; Naha, Japón, febrero 1; Yokohama, Japón, febrero 4. El primer caso es reportado por las autoridades de Hong Kong el 1 de febrero, quedando entonces el Diamond Princess inmovilizado desde el día 4 de febrero. A continuación, vemos la cronología del brote.
- El día 20 de enero procedente de Shenzen, provincia China de Guangdong, se embarca en Yokohama Japón un hombre de 80 años (señor “A”), quien un día anterior presentó un cuadro clínico de tos y fiebre. El señor “A” deja el barco el 25 de enero.
- El día primero de febrero se confirma en Hong Kong como positivo a Covid-19 al señor “A”, dando ese mismo día el aviso al personal encargado del crucero. Sin embargo, se decide retrasar la noticia a los pasajeros y a la tripulación hasta el día 3 de febrero, manteniendo los dos primeros días de febrero las actividades normales del crucero, esto es: alberca abierta, gimnasio abierto, restaurantes buffet, fiestas y espectáculos nocturnos con normalidad. El cuatro de febrero se da la orden de cuarentena dentro de la embarcación. Finalmente, el desembarco total de pasajeros se realiza a finales de marzo.
- A finales de marzo se contabiliza un total de 711 personas infectadas dentro del crucero.
1.1. Registro de los casos y de las pruebas realizadas
Los criterios para aplicar las pruebas fueron, principalmente, que se tengan síntomas y que se haya tenido contacto cercano a una persona contagiada por Covid-19. La tabla 1 nos muestra los datos recopilados
Tabla 1
Tabla de contagios y pruebas realizadas
|
Fecha |
# de test |
Acumulado test |
Positivos/día |
Acumulado positivos |
|
Febrero 5 |
31 |
31 |
10 |
10 |
|
Febrero 6 |
71 |
102 |
10 |
20 |
|
Febrero 7 |
171 |
273 |
41 |
61 |
|
Febrero 8 |
6 |
279 |
3 |
64 |
|
Febrero 9 |
57 |
336 |
6 |
70 |
|
Febrero 10 |
103 |
439 |
65 |
135 |
|
Febrero 11 |
- |
- |
- |
- |
|
Febrero 12 |
53 |
492 |
39 |
174 |
|
Febrero 13 |
221 |
713 |
44 |
218 |
|
Febrero 14 |
- |
- |
- |
- |
|
Febrero 15 |
217 |
930 |
67 |
285 |
|
Febrero 16 |
289 |
1219 |
70 |
355 |
|
Febrero 17 |
504 |
1723 |
99 |
454 |
|
Febrero 18 |
681 |
2404 |
88 |
542 |
|
Febrero 19 |
607 |
3011 |
79 |
621 |
|
Febrero 20 |
52 |
3063 |
13 |
634 |
|
Marzo 1 |
- |
- |
- |
711 |
La tabla 2 nos muestra el número de asintomáticos y sintomáticos a partir del día 15 de febrero de 2020.
Tabla 2
Casos de sintomáticos y asintomáticos
|
Fecha |
# de Sintomáticos/día |
# de Asintomáticos/día |
Acumulado de asintomáticos |
|
Febrero 15 |
29 |
38 |
73 |
|
Febrero 16 |
32 |
38 |
111 |
|
Febrero 17 |
29 |
70 |
181 |
|
Febrero 18 |
23 |
65 |
246 |
|
Febrero 19 |
11 |
68 |
314 |
|
Febrero 20 |
7 |
6 |
320 |
1.2. Aplicación de la estadística inferencial y obtención del coeficiente de propagación
Recordando el teorema total de probabilidad (Spiegel, 1985) el cual establece que para un espacio muestral $S$ que contiene a los eventos mutuamente excluyentes $B,A_1,A_2,A_3,...,A_n$,la probabilidad de que suceda el evento $B$ está dada por la siguiente fórmula: $P(B)=\sum_{i=1}^{n}P(B|A_{i})$ , donde $P(B|A_{i})$ es la probabilidad de que exista el evento $B$, dado que el evento $A_i$ ha ocurrido. Ahora apliquemos lo anterior al caso donde los eventos serán los contagios ocurridos (Mansky et al 2020) en crucero Diamond Princess:
- Entonces, sea $C_{d}=1$ el evento una persona fue contagiada por el virus SARS-CoV-2 el día $d$, si no lo fue, este evento se designa por $C_d=0$.
- $P(C_d)$ será entonces la probabilidad de que alguien se contagie el día $d$.
- Si una persona se realiza la prueba el día $d$ lo registramos como $T_d=1$ y $T_d=0$ si no se realiza la prueba.
- $R_d=1$ representará el resultado positivo de la prueba y $R_d=0$ si el resultado de la prueba es negativo.
Por la ley de probabilidad total, la probabilidad de contagio puede escribirse como:
|
$$ P(C_{d}=1)=P(C_d=1|R_d=1)*P(R_d=1)+P(C_d=1|R_d=0)*P(R_d=0) $$ |
Esto es, la probabilidad de haber sido contagiado de SARS-CoV-2 el día $d$ es la probabilidad de estar contagiado haberse hecho la prueba y haber salido positivo, más, la probabilidad de estar contagiado haberse hecho la prueba y que el resultado sea negativo. Ahora tenemos que tener en cuenta que
|
$$ P(R_d=1)=P(R_d=1|T_d=1)*P(T_d=1), $$ |
es la probabilidad de salir positivo en la prueba, habiéndose hecho la prueba. Y que
|
$$ P(R_d=0)=P(R_d=0|T_d=1)*P(T_d=1) $$ |
es la probabilidad de salir negativo condicionada a haberse hecho la prueba. Por último,
|
$$ P(C_d=1|R_d=0)*P(R_d=0), $$ |
representa la probabilidad de estar contagiado habiendo salido negativo en la prueba, esto es, un falso negativo.
Por otro lado, veamos que las cantidades que se pueden medir de manera directa son:
- La probabilidad de que no hacerse la prueba $P(T_d=0)$, la cual está relacionada con el no contacto con personas contagiadas y la no presentación de síntomas.
- La probabilidad de hacerte la prueba $P(T_d=0)$, la cual depende de si hubo contacto con algún contagiado o si se presentan síntomas.
- La probabilidad de salir negativo en la prueba $P(R_d=0|T_d=1)$, esto es se presentaron síntomas y/o se mantuvo contacto con algún contagiado de Covid-19, se realizó la prueba y el resultado fue negativo.
- La probabilidad de salir positivo en la prueba $P(R_d=1|T_d=1)$.
Ahora la cantidad sujeta a discusión es, $P(C_d=1|T_d=0)$ , ya que es precisamente la cantidad que no podemos medir si no se desarrollan síntomas, esto es, la probabilidad de estar contagiado sin haberse hecho la prueba por no presentar síntomas. Para calcular la cantidad anterior procedamos de la siguiente manera, descompongamos a los enfermos de Covid-19 en dos tipos de pacientes:
- Los que presentan síntomas (sintomáticos).
- Los que no presentan síntomas (asintomáticos).
Una persona contagiada de Covid-19 y diagnosticada el día $d$ se designa por $S_d$ si es sintomático y $A_d$ si es asintomático. Se tiene que cumplir que $C_d=S_d+A_d$ , consecuentemente,
|
$$ P(C_d=1)=P(S_d=1)+P(A_d=1) $$ |
La fracción de asintomáticos está dada por
|
$$ P(A_d=1)=\alpha P(C_d=1) $$ |
Luego, combinando las ecuaciones (5) y (6) se obtiene
|
$$ P(C_d=1)=\frac{P(S_d=1)}{1-\alpha } $$ |
Puesto que la probabilidad de asintomáticos es menor a la probabilidad total de contagios se tiene que $0< \alpha < 1$ y la literatura, reporta Godio et al. (2020), $\alpha=[0.25\:0.45$].
Pasemos ahora al análisis dinámico del contagio dentro del crucero. El modelo SIR o teorema umbral de epidemiología es una primera aproximación que predice la evolución de una enfermedad contagiosa en una población que se supone fija y que además se supone también que una vez contraída la enfermedad la persona se vuelve inmune, esto es, no hay posibilidades de reinfección. En el caso del crucero Diamond Princess se cumple con la población constante y para evitar la reinfección se aisló a los enfermos y se les retiró, evitando así la exposición nuevamente al virus. El modelo coloca a la población en bloques o compartimentos dependiendo de su estado de salud. Las divisiones se establecen de la siguiente manera:
- S denotará a la población susceptible, esto es, la población sana.
- Cuando la población sana contraiga el virus pasará al compartimento de los infectados representados por I.
- Luego, la población infectada tendrá necesariamente que recuperarse o fallecer, en cualquiera de los dos casos ya no representarán una fuente de infección así que se considerará como población retirada R, que finalmente es lo que hicieron las autoridades sanitarias, retirar a os infectados para evitar la re-infección, dado que como se ha observado y reportado (J. Dan et al 2021) no hay inmunidad una vez contraído el virus.
La figura (1), representa gráficamente el flujo de la población hacia los compartimentos:
Figura 1
Flujos de entrada y salida a los compartimentos

Al tratarse de un sistema cerrado la población total, N, permanecerá fija. Ahora, la rapidez con la que se propaga el virus será proporcional a la interacción de la población entre sí, esto es, la población susceptible interactuando con la población infectada, lo cual se representa por el producto S*I. Entonces, la rapidez con la que la población susceptible o sana decrece se expresa en la ecuación (8), la población infectada aumenta de acuerdo a la interacción con la población sana y disminuye conforme salen de la enfermedad y se representa mediante la ecuación (9) y finalmente la rapidez de retiro depende del tamaño de la población infectada y del tiempo de recuperación de la enfermedad, ecuación (10).
|
$$ \frac{dS(t)}{dt}=-\beta S(t)I(t), $$ |
|
$$ \frac{dI(t)}{dt}=\beta S(t)I(t)-\mu I(t), $$ |
|
$$ \frac{dR(t)}{dt}=\mu I(t), $$ |
Donde $\beta > 0$ es el parámetro de transmisión, $\mu > 0$ es la tasa de retiro y $S_0, I_0, R_0$ son los valores iniciales para cada compartimento de la población. La tasa de retiro se toma como el inverso del tiempo que dura la enfermedad (Godio et al. 2020), así que en este caso $\mu =\frac{1}{15} = 0.066667$ ya que el paciente infectado tardaba 15 días en recuperarse.
Para obtener el parámetro de transmisión podemos aproximar la ecuación (9) de la siguiente manera
|
$$ I'\approx \beta S(0)I(0) $$ |
Despejando $\beta$
|
$$ \beta \approx \frac{I'(0)}{S(0)I(0)} $$ |
Apliquemos lo anterior, empecemos por tener en cuenta que el brote de Covid-19 dentro del crucero comenzó con una persona enferma el día 20 de enero, sin embargo, los registros empezaron el día cinco de febrero cuando se confirmaron 10 personas infectadas, así que se toma el día cinco de febrero como $T=0$, luego $I(0)=10$ y $S(0)$ donde la cantidad $I'(0)$ la podemos aproximar por el cociente
|
$$ I'(0)=I(1)-I(0)/1=10, $$ |
sustituyendo en la ecuación (12) encontramos que
|
$$ \beta =10/(3701)(10)=2.710^{-4} $$ |
2. Resultados y Discusiones
En base a las políticas que se tomaron de realizar la prueba para detectar a una persona infectada de Covid-19 si la persona tenía síntomas o si había estado en contacto con alguna persona infectada se calculan las siguientes probabilidades y el parámetro alfa, el cual es un factor de proporcionalidad de la población infectada asintomática con respecto al número total de infectados.
Tabla 3
Probabilidades calculadas y el parámetro alfa
|
Fecha |
$ P(T_d=1) $ |
$ P(R_d=1|T_d=1) $ |
$ P(C_d=1) $ |
$ P(A_d=1) $ |
$ \alpha $ |
|
02/05/20 |
0.0083 |
0.3132 |
0.3132 |
- |
- |
|
02/06/20 |
0.00274 |
0.1934 |
0.1934 |
- |
- |
|
02/07/20 |
0.0735 |
0.2236 |
0.2236 |
- |
- |
|
02/08/20 |
0.0751 |
0.2290 |
0.2290 |
- |
- |
|
02/09/20 |
0.0905 |
0.2077 |
0.2077 |
- |
- |
|
02/10/20 |
0.01182 |
0.3071 |
0.3071 |
- |
- |
|
02/11/20 |
0.1182 |
0.3071 |
0.3071 |
- |
- |
|
02/12/20 |
0.1325 |
0.3532 |
0.3532 |
- |
- |
|
02/13/20 |
0.1921 |
0.3055 |
0.3055 |
- |
- |
|
02/14/20 |
0.2066 |
0.3054 |
0.3054 |
- |
- |
|
02/15/20 |
0.2694 |
0.3062 |
0.5622 |
0.256 |
0.0209 |
|
02/16/20 |
0.3532 |
0.2910 |
0.6030 |
0.312 |
0.0321 |
|
02/17/20 |
0.5413 |
0.2429 |
0.6419 |
0.399 |
0.0519 |
|
02/18/20 |
0.7552 |
0.2253 |
0.6793 |
0.454 |
0.0772 |
|
02/19/20 |
0.9459 |
0.2061 |
0.7121 |
0.506 |
0.0986 |
|
02/20/20 |
0.9622 |
0.2069 |
0.7119 |
0.505 |
0.1005 |
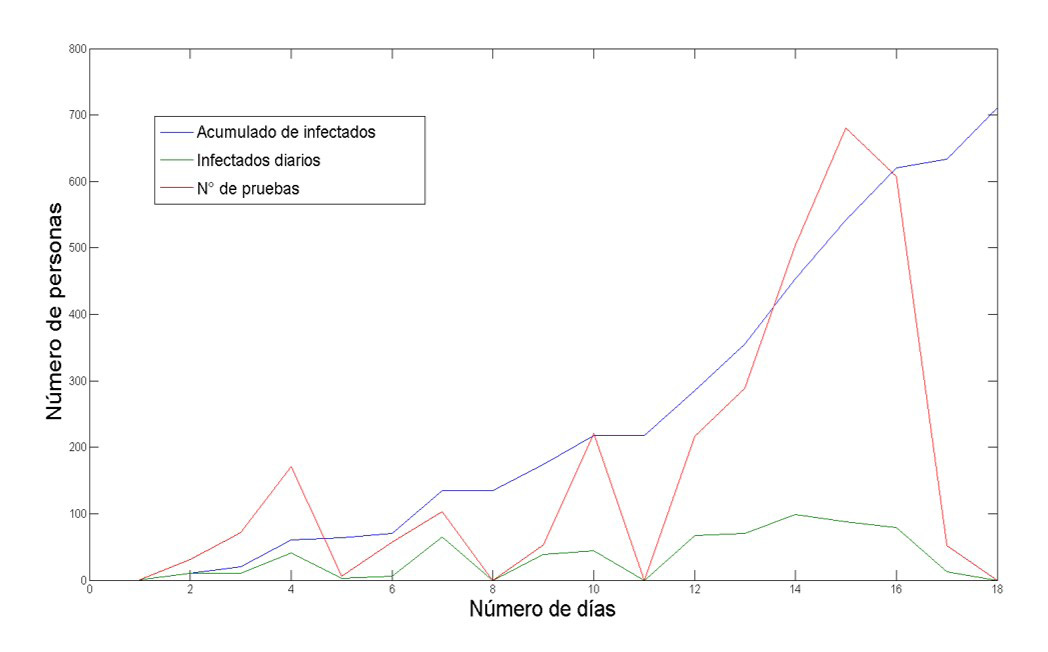
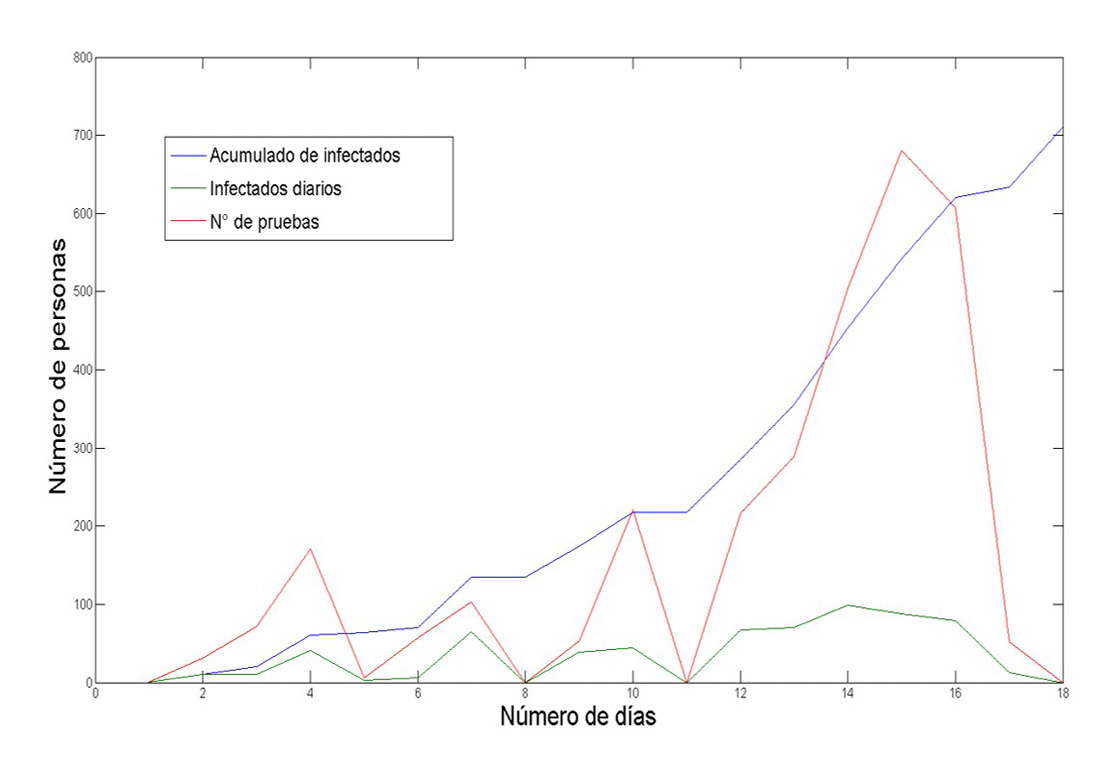
Las autoridades japonesas establecieron que las pruebas se aplicarían a las personas que presentaran síntomas o que hayan estado en contacto con algún enfermo por covid-19. En la tabla (3) la columna dos muestra la fracción de individuos que fueron sometidos a la prueba por Covid-19, los datos revelan que casi la totalidad de la población se hizo la prueba, lo que quiere decir que la mayoría de la población presentó síntomas o estuvo en contacto con algún enfermo por Covid-19. En la columna tres está la fracción de individuos que salieron positivos al hacerse la prueba de Covid-19. En la columna cinco se aprecia la porción de asintomáticos, donde, hay un retraso en los datos debido al tiempo en que tardan en aparecer los síntomas. En la columna cuatro se muestra, entonces, la probabilidad de estar infectado siendo sintomático o asintomático. Finalmente usando la ecuación (6) en la última columna vemos la evolución diaria del parámetro α, el cual siempre va en ascenso. El comportamiento de la columna uno se visualiza mejor en la figura (2), donde también podemos ver que aún con las medidas de aislamiento hay un crecimiento en la velocidad de propagación del virus SARS-CoV-2, por lo que se deduce que el contagio es considerablemente agresivo a pesar de aislar a la población.
Figura 2
Comportamiento de la infección provocada por el Covid-19 del crucero
2.1. Implementación del modelo SIR
El parámetro de transmisión, β, encontrado a partir de los datos reportados se utiliza en la implementación del modelo SIR, este parámetro β es único para cada problema, ya que está en función del tamaño de la población, lo que significa que si la población es grande la enfermedad se transmitirá más rápido. En este trabajo se implementa el modelo SIR para obtener la evolución del contagio en un escenario de no-confinamiento. En la figura (3) se muestra la proyección total de la evolución de los tres bloques de manera simultánea en el caso hipotético de que no se hubiera declarado la cuarentena. Veamos que debido al parámetro β el número de infectados alcanza su máximo alrededor del día diez y que la evolución de la enfermedad dura aproximadamente un mes. Lo anterior nos reafirma nuevamente de la rapidez del contagio que tiene el virus SARS-CoV-2.
Figura 3
Evolución del Covid-19 en un escenario sin control
3. Conclusiones
El cálculo del coeficiente de propagación en un entorno cerrado proporciona una importante primera aproximación, ya que se visualiza la potencialidad del virus para dispersarse entre la población. El cálculo de la velocidad de propagación cuando aún existía una interacción no limitada dentro del crucero advierte de la peligrosidad del no confinamiento y de un apresurado regreso a las actividades normales. La tendencia creciente del parámetro que es directamente proporcional con los pacientes asintomáticos, favorece a que el virus SARS-CoV-2 se disperse sin dejar rastros de su paso.
A principios de marzo del 2020 el saldo que dejó el nuevo virus SARS-CoV-2 en el Diamond Princess fué de 711 personas infectadas y 13 personas fallecidas, dando una idea ya de la capacidad de contagio del virus y de su letalidad, así que el tener herramientas de proyección y técnicas estadísticas que involucren a los asintomáticos es esencial para que una correcta toma de decisiones mitigue el efecto de la pandemia. El entorno en que se produjeron esos contagios también es un indicador de cuáles son los lugares que producen un ambiente propicio para la transmisión del virus, ya que, a más de un año de la pandemia ya se tiene claro que dentro de los principales mecanismos para la propagación del SARS-Cov-2 están los aerosoles producidos al hablar (Dbouk et al, 2020), por lo que, la decisión de mantener abiertas durante dos días las actividades recreativas en lugares cerrados como gimnasios, teatros, restaurantes, cines y salones de baile donde se acumulan en el ambiente las micro-gotículas de saliva resultó ser una decisión equivocada para lo que ahora sabemos. Lo anterior junto con el presente estudio nos lleva a concluir que los lugares cerrados y con aglomeración de personas son potencialmente peligrosos para la transmisión del SARS-Cov-2. Otro problema con el que se encuentran las autoridades sanitarias es el número real de personas infectadas, ya que las personas infectadas que no presentan síntomas del Covid-19 permanecen invisibles para los registros e incrementan la velocidad de con la que se propaga el virus en la población.
Agradecimientos
Agradecemos a la Universidad del Mar y al Tecnológico de Estudios Superiores Oriente del Estado de México por las facilidades otorgadas.
Referencias
Black, A.J. y McKane, A.J. (2010). Stochasticity in staged models of epidemics: quantifying the dynamics of whooping cough. Journal of the Royal Society Interface 7(49), 1219-1227. https://doi.org/10.1098/rsif.2009.0514
Colizza, V. y Vespignani, A. (2008). Epidemic modeling in metapopulation systems with heterogeneous coupling pattern: Theory and simulations. Journal of Theoretical Biology 251(3), 450-467. https://doi.org/10.1016/j.jtbi.2007.11.028
Dan, J.M.; Mateus, J.; Kato, Y.; Hastie, K.M.; Yu, E.D.; Faliti, C.E.; Grifoni, A.; Ramirez, S. I.; Haupt, S.; Frazier, A.; Nakao, C.; Rayaprolu, V.; Rawlings, S. A.; Peters, B.; Krammer, F.; Simon, V.; Ollmann Saphire, E.; Smith, D. M.; Weiskopf, D.; Sette, A. y Crotty, S. (2021). Immunological memory to SARS-CoV-2 assessed for up to 8 months after infection. Science, 371(6529), eabf4063. https://doi.org/10.1126/science.abf4063
Dbouk, T. y Drikakis, D. (2020). On coughing and airborne droplet transmission to humans. Physics of Fluids, 32(5), 053310. https://doi.org/10.1063/5.0011960
De Castro, C. (2020). Modelo SIR de la epidemia de Covid-19 en Colombia – Proyección según diversos escenarios. Revista de Salud Pública, 22, 1-9.
Godio, A.; Pace, F. y Vergnano, A. (2020). SEIR Modeling of the Italian Epidemic of SARS-CoV-2 Using Computational Swarm Intelligence. International Journal of Environmental Research and Public Health. 17(10), 05-18. https://doi.org/10.3390/ijerph17103535
Gómez-Osorio, H.; Isaza, S. y Osorio, P. (2021), Estimación de parámetros, análisis de sensibilidad y validación del modelo SIR aplicado a datos históricos del virus A(H1N1) en México. Cuadernos de Ingeniería Matemática, 1(1), 1-7. http://hdl.handle.net/10784/29843
Manski, C.F. y Molinari, F. (2020). Estimating the COVID-19 infection rate: Anatomy of an inference problem. Journal of Ecomometrics 220(1), 181-192. https://doi.org/10.1016/j.jeconom.2020.04.041
Lennette, E. H.; Halonen, P.; Murphy, F. A.; Balows, A. y Hausler Jr., W. J. (2012). Laboratory Diagnosis of Infectious Diseases Principles and Practice Volume II Viral, Rickettsial, and Chlamydial Disease. Springer.
Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S. S.; Wang, M. H.; Cai, Y.; Wang, W.; Yang, L.; He, D. (2020). A conceptual model for the coronavirus disease 2019 (COVID-19) outbreakin Wuhan, China with individual reaction and governmental action. International Journal of Infectious Diseases, 93, 211–216. https://doi.org/10.1016/j.ijid.2020.02.058
Mizumoto, K.; Kagaya, K.; Zrebski, A.; Chowell G. (2020). Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Euro Surveillance, 25(10), pii=2000180. https://doi.org/10.2807/1560-7917.
Oran, D.P. y Topol, E.J. (2020). Prevalence of asymptomatic SARS-CoV-2 infection : a narrative review. Annals of Intern Medicine, 173(5), 362-367. https://doi.org/10.7326/M20-3012
Xu, P.; Qian, H.; Miao, T.; Yen, H.L.; Kang, M.; Cowling, B.J. y Li, Y. ( Transmission routes of Covid-19 virus in the Diamond Princess Cruise Ship. medRxiv https://doi.org/10.1101/2020.04.09.20059113
Fang, Z.; Huang, Z.; Li, X.; Zhang, J.; Lv, W.; Zhuang, L.; Xu, X. y Huang, N. (2020). How many infections of Covid-19 there will be in the “Diamond Princess” Predicted by a virus transmisión model base on the simulation of crowd flow. arXiv. https://doi.org/10.48550/arXiv.2002.10616
Zill, D.G. (1997). Ecuaciones diferenciales con aplicaciones al modelado. Thompson