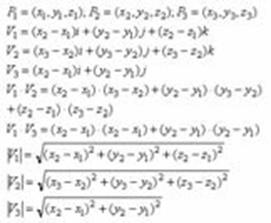Modelo Óptico de Estéreo Visión usando Visión por Computadora
Marco Antonio Moreno Armendáriz , Julián Aguilar Luna, Eduardo Gómez Ramírez & Xavier Vilasis Cardona
1
Laboratorio
de
Investigación
y Desarrollo de Tecnología Avanzada (LIDETEA)
UNIVERSIDAD
LA
SALLE
E-mail: egr@ci.ulsa.mx
 1
U. Ramon Llull, Departament d'Electrónica, Enginyeria i Arquitectura La Salle,
1
U. Ramon Llull, Departament d'Electrónica, Enginyeria i Arquitectura La Salle,
Pg. Bonanova 8, 08022 Barcelona, España,
E-mail: xvilasis@salleURL.edu
Recibido:Julio de 2003. Aceptado: Julio de 2003.
RESUMEN
A través de los tiempos, el hombre ha observado y estudiado la naturaleza para entender y replicar algunos de sus comportamientos por medio de
elementos artificiales. Los resultados obtenidos lo han ayudado a simplificar sus tareas en algunas áreas de trabajo.
Gracias a los estudios tecnológicos hoy día se cuenta con herramientas de apoyo que tienen funciones similares a las funciones humanas, tales como las
memorias permanentes que simulan una de las tantas actividades cerebrales, brazos mecánicos que simulan una de las dos extremidades humanas, etc. La
visión no es la excepción de estudio, en el presente trabajo se da a conocer una propuesta de desarrollo y aplicación de la visión artificial.
Palabras claves: Visión por computadora, estéreo visión, cinemática.
ABSTRACT
The research of robotics and computer vision aims to realize some aspects of human functions into mechanical systems. Trying to reproduce these
functions allow researchers to reach very simple and functional algorithms to be used within the industry.
Currently there are appropriate technologies based on this idea, like a special memory with the capaci- ty to simulate some kind of brain activities or
robot manipulators used to reproduce simple repetitive tasks. The computer vision aims to produce new schemes to bring autonomy and more flexibility to
these sys- tems. In this paper a new computer vision model is developed with the ability to locate automatically the position in the space of an
unknown point.
Keyword: Computer vision, stereovision, kinematics.
INTRODUCCIÓN
En tiempos recientes se ha llevado a cabo la automatización de diferentes tipos de procesos, como los industriales o los administrativos. Esto trae
como beneficio la reducción del tiempo, gracias al avance en los sistemas de cómputo y al surgimiento de nuevas tecnologías, como
son: los sistemas de visión por computadora, la lógica difusa y las redes neuronales.
Estos nuevos desarrollos han facilitado el tra- bajo del ser humano haciéndolo más eficiente. Existen diversos tipos de sistemas de visión por
computadora, catalogados por el número y tipo de sensores. Se componen principalmente de cámaras de video especializadas, encargadas de realizar la
adquisición de las imágenes y de un conjunto de algoritmos cuyo objetivo es extraer de éstas la información necesaria para el proceso a realizar.
Actualmente, la mayoría de los sistemas de visión por computadora que se emplean se encuentran instalados en las plantas manufactureras para efectuar
tareas de control de la calidad de productos, esto puede llevarse a cabo mediante algoritmos de conteo y detección de patrones, los cuales se seleccio-
nan por un supervisor experto, de acuerdo con las necesidades de cada proceso. Para este tipo de actividades es suficiente utilizar una sola cámara o
sensor, ya que no es necesario cono- cer la ubicación de un objeto en el espacio.
Por otra parte, existen tareas como en una línea de producción automatizada donde un conjunto de robots se encargan de elaborar un producto en etapas
previamente programa- dos con rutinas especificas, que ejecutan repeti- damente. Sin embargo, si se deseara imple- mentar una celda de manufactura
flexible, donde los robots tuvieran la capacidad de realizar diferentes actividades, sin la necesidad de tener que reprogramarlos. Una opción sería
implementar algunas de las tecnologías ante- riormente mencionadas con la finalidad de brindar mayor flexibilidad al robot. Un ejemplo de esta tecno-
logías son los sistemas de visión por computadora. Una de las tareas más comunes de estos sistemas es obtener la posi- ción del órgano terminal del
robot en el espacio de trabajo mediante la información visual. El valor obtenido de la posición se incorpora en el lazo de control del robot para que
éste lleve a cabo la tarea asignada.
Con la idea general de reconstrucción de imá- genes 3D a partir de 2D se hace necesario el tener al menos dos patrones lógicos que ayu- den a analizar
el comportamiento de las imá- genes, bajo esta estructura muchos experimen- tos publicados se han llevado a cabo, como la estructura a partir del
movimiento[1,2], estéreo correspondencia [3-7] y forma [8].
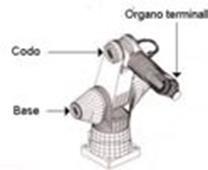
Figura 1. Partes del robot A465.
En el presente trabajo se diseñará un sistema de visión por computadora para obtener la infor- mación necesaria para el modelo óptico de estéreo visión
propuesto. Finalmente, se imple- menta este modelo para obtener visualmente algunos parámetros del modelo cinemático del robot A465. (Fig. 1)
l. PLATAFORMA DE VISIÓN.
I.1 Sistema de visión artificial.
El sistema de estéreo visión está formado por los siguientes elementos:
1. Dos cámaras análogas Pulnix TM72-EX
2. Dos lentes Cosmicar C815B
3. Una tarjeta de video NI PCI-1408
4. Una computadora Dell Optiplex GX240.

Figura 2. Sistema de visión por computadora.
Con el fin de reducir la cantidad de informa- ción a procesar, la escena y el robot se cubren en color negro (ver Figura 3). Después, se colo- can tres
marcas visuales (círculos blancos) sobre las partes indicadas en la Figura 1. A par- tir de estas marcas se obtendrá toda la informa- ción visual
necesaria para ubicar la posición en el espacio del órgano terminal del robot A465.
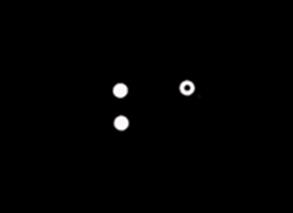
Figura 3. Imagen capturada con el sistema de visión por computadora
I.2 Distorsión radial
Las lentes utilizadas para las cámaras son las Cosmicar C815b, que tienen un área visual de 1194x1728 mm, a 2 m de distancia, de un objeto enfocado. La
convexidad de las lentes hace que las imágenes que pasan por ellas tengan una distorsión radial, como puede observarse en la Figura 4:

Figura 4. Imagen con distorsión radial.
Dado que el modelo óptico de estéreo visión se basa en la información extraída de imá- genes, es necesario tener una imagen sin dis- torsión. Para
eliminar la distorsión de las lentes utilizamos el algoritmo de corrección de imá- genes presentado por Chavarría, Soria y Wiederhold [9], que usa la
siguiente expresión matemática:
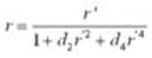
(Ec.1)
Donde r es el radio de corrección y r’ es el radio de distorsión. Experimentalmente, se ob- tienen los valores de corrección
de la imagen que son: d2 = -6.166e-7 y d4 = 2.083e-12. Así, las coordenadas sin
distorsión se obtienen mediante:
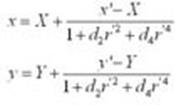
(Ec.2)
Donde (x’,y’) son las coordenadas de los centroides de las marcas con distorsión, (X , Y) es la coordenada del
centro de la imagen que, para este caso, (320,240) y (x,y) son las nuevas coordenadas sin distorsión. En la Figura 5 se muestra la imagen sin
distorsión.

Figura 5. Imagen con distorsión radial eliminada.
ll. ALGORITMOS DE VISIÓN POR COMPUTADORA
El sistema de visión por computadora es el encargado de calcular el centroide de las tres marcas visuales que aparecen en las imágenes capturadas con
las cámaras analógicas (ver Figura 6).

Figura 6. Diagrama de proceso de los algorit- mos de visión por computadora.
El proceso de obtención del centroide se divide en cinco etapas (ver Figura 7):
1. Binarización de la imagen.
2. Redimensionamiento de la imagen binarizada.
3. Segmentación de las marcas visuales.
4. Obtención de los centroides de las marcas visuales.
5. Etiquetado de las marcas visuales.
II. 1 Binarización
La imagen capturada por las cámaras analógi- cas se envía a la tarjeta PCI-1408 que se encar- ga de digitalizarla y binarizarla.
II. 2 Redimensionamiento
Completado el proceso de binarización se cuen- ta con una imagen de 640x480 píxeles, esta cantidad podría incrementar mucho el tiempo de procesamiento
si se maneja durante el proceso. Dado que el objetivo es obtener solamente el centroide de las marcas visuales, la imagen se reduce (redimensiona) de
tal forma que los píxeles resultantes proporcionen esta informa- ción. Para redimensionar la imagen utilizamos la siguiente ecuación:
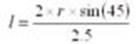
(Ec.3)
donde r es radio de los círculos en píxeles y I el número de píxeles.
Para esta aplicación r = 13 píxeles, por lo que l = 7 píxeles, dando como resultado que una imagen redimensionada es de 91x68 píxeles.
II. 3 Segmentación
En esta parte del proceso las marcas visuales se separan para después calcular su centroide y posteriormente etiquetarlas. Este proceso se lleva a cabo
mediante una búsqueda de la 8- conexidad,[10,11] que se encarga de agrupar a los puntos en tres objetos separados. Esto es posible dado que
las marcas visuales se encuentran en las extremidades del robot A465, pudiendo garantizar que éstas nunca se enci- marán.

Figura 7. Etapas del proceso de los algoritmos de visión por computadora.
II. 4 Cálculo del centroide
Para la obtención del centroide de las marcas visuales se localizan los puntos máximos y mínimos horizontales y verticales, (ver Figura 8) siendo el
centroide la intersección de ellas.

Figura 8. Cálculo de los valores máximos y mínimos
El valor de los centroides se obtiene con:
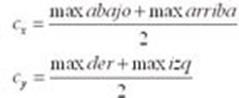
(Ec.4)
|
Objetos
|
Centroides
|
|
|
u
|
v
|
|
Objeto O1
|
267.5
|
213
|
|
Objeto O2
|
269
|
283
|
|
Objeto O3
|
411
|
207.5
|
|
|
En la Tabla 1, se presenta el valor de los cen- troides para el ejemplo de la Figura 7.
Tabla
1. Listado de los objetos y el valor de sus centroides.
II.5 Etiquetado de las marcas
Por último, los centroides se etiquetan depen- diendo el lugar en el que se encuentren coloca- dos sobre el robot A465 (ver Figura 1).

Figura 9.Segundo criterio usado para etiquetar las marcas visuales.
Para etiquetar los objetos, se toma el valor de la coordenada (u,v) del primer centroide de la Tabla 1, con estos valores se posiciona sobre
la imagen binarizada, y si el bit en esa posición es de color negro, se etiqueta como órgano ter- minal, de no ser así se toma el siguiente
valor hasta encontrar el centroide con estas caracte- rísticas. Para los dos puntos restantes se utiliza el criterio de posición, suponemos que uno de
ellos siempre estará por arriba del otro (ver Figura 9). Bajo este criterio se toman los valores de la coordenada v de la Tabla 1, nombrando al de
mayor valor base y el restante codo como se muestra en la Tabla 2.
|
Etiqueta
|
Centroide
|
|
|
u
|
v
|
|
Codo
|
267.5
|
213
|
|
Base
|
269
|
283
|
|
Órgano terminal
|
411
|
207.5
|
Tabla
2. Etiquetado de las marcas visuales
Con este proceso la computadora tiene la capacidad de correlacionar cada una de las marcas visuales con su correspondiente parte en el robot.
Hasta este punto se han descrito las diferen- tes herramientas encargadas del procesamien- to de las imágenes para obtener la información visual que se
usará en el modelo óptico de estéreo visión.
III. MODELO ÓPTICO DE ESTÉREO VISIÓN
En esta sección presentaremos nuestra princi- pal contribución. El modelo óptico de visión estéreo a cargo de localizar un punto descono- cido en el
espacio, con base en la información
visual. Para ello se requiere conocer el cen- troide (u,v) de las marcas visuales ubicadas en el codo y órgano terminal del robot, además de
los ángulos de rotación
0
1a,
0
1b de las cámaras (ver Figuras 10 y 13).

Figura 10. Proceso realizado por el modelo óptico de estéreo visión.
III. 1 Modelo óptico de la cámara
Con base en el modelo del telescopio de Gali- leo [12], en la Figura 11 se plantea un modelo geométrico que nos ayudará a obtener las dis- tancias
entre el robot A465 y las cámaras.
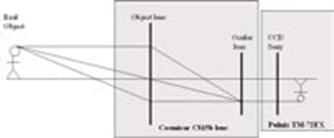
Figura 11. Diagrama óptico de la cámara Pulnix con lentes Cosmicar C815B.
Con base en el modelo óptico de la Figura 12 obtenemos las siguientes ecuaciones:
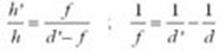
(Ec.5)

Figura 12. Variables definidas para el modelo óptico
III.1.1 Obtención de los parámetros f ,d’
De la ecuación 4 se obtienen las siguientes ex- presiones:
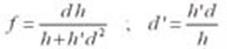
(Ec.6)
Experimentalmente se obtienen los valores para d,h,h,h’, posteriormente se sustituyen en la ec. 6, obteniendo f ,d’,
teniendo a h en centíme- tros y las unidades de h’ en píxeles. Por ello hacemos uso de un factor de conversión de unidades de píxel a
centímetro, del cual resultó experimentalmente que:
f
pix-cm
= 0.002708333.
Con este factor se obtuvieron los siguientes valores:
Con base en el diagrama geométrico del modelo óptico, (ver Figura 13) se obtienen las ecuaciones para el cálculo de las distancias:
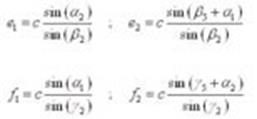
(Ec.7)
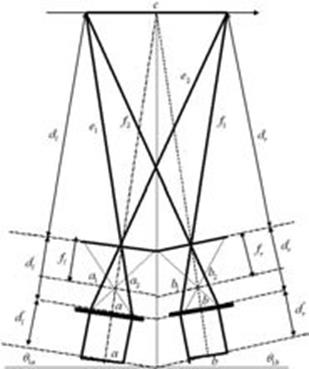
Donde, los ángulos a1,a2,b2,b5,g2,g5 se defi- nen por los triángulos determinados por las lí- neas c,e1,e2 ,f1,f2 (ver Figura 14) Estos valores se usarán en el siguiente paso.
 f = 0.585091 cm d’= 1.704799 cm
f = 0.585091 cm d’= 1.704799 cm
III.2 Distancia entre cámara y escena
En este paso resulta el valor de las distancias (e1,e2) y (f1, f2 ), que son las entre marcas visuales colocadas en las articulaciones del objeto ob- servado y las cámaras (ver Figura 13). Donde, c
es la distancia del codo al órgano terminal.
Hay que resaltar que este punto es uno de los más importantes, ya que las distancias calcu- ladas se obtienen cuando el robot se encuentra en posición
de inicio, de la que podemos obte- ner una coordenada de referencia.
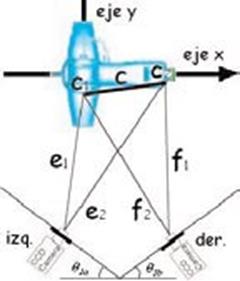
Figura 13. Distancia entre las cámaras y la escena.
Figura 14. Diagrama geométrico del modelo óptico
Obtención de la posición de un punto en el espacio.
Una vez que se han calculado las distancias (e1,e2) y (f1,f2), se
elige un punto conocido o de referencia, que será el centroide de la marca visual, encontrándose en el codo del robot A465 (ver Figura 15).
Posteriormente, éste se mueve, de tal forma que ahora la posición del órgano terminal es desconocida (ver Figura 16).
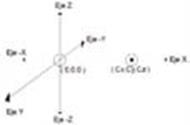 Así:
Así:
x=c’cos (
a
’) y=c’cos(
a
’)
(Ec.9)
Figura 15. Cuadro cartesiano a partir del codo
De ahí que, con esta nueva referencia, la posi- ción desconocida del órgano terminal es (Cx,CY,0).
III.3 Coordenada z
Para obtener el valor de la coordenada z, suponemos que ambas cámaras están mon- tadas a la misma altura, con lo que se establece la siguiente
relación:
z = k
r
uL =kruR
(Ec.8)
donde:
• Kr : es el factor de conversión de pixel a cm.
• uL y uR son las coordenadas en ambas imá- genes con respecto al eje z, para el centroide de la marca visual que
se encuentra en el órgano terminal.
III.4 Coordenadas x & y
Para obtener las coordenadas (x,y) se hace uso de un modelo geométrico análogo al mostrado en la Figura 14 para el calculo de las distancias c’ y el ángulo a‘ fórmula como se muestra en la Figura 16:
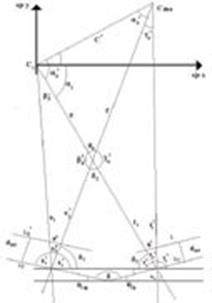
Figura 16. Valores requeridos para obtener las coordenadas (x,y).
En esta sección se implementan nuestros mo- delos en el robot CRS A465 (ver Figura 17).
IV. 1 Calculo de parámetros cinemáticos usan do información visual
Cualquier robot puede detallarse cinemática- mente mediante la medición de cuatro variables que describen completamente cada articula- ción. Dos
describen su propia articulación, y dos describen la conexión con las articulaciones. Estas variables se definen por la notación de Denavit-Hartenberg
[13]. Aplicando esta con- vención obtenemos el modelo cinemático para el robot A465 (ver Figura 17). El modelo se probó experimentalmente.
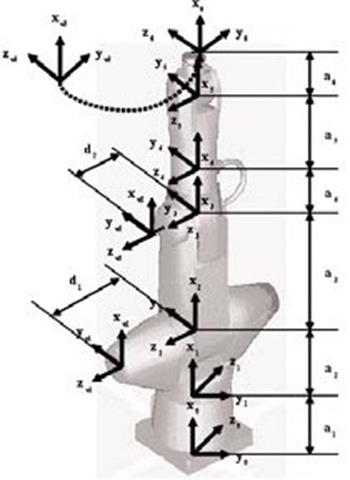
Figura 17. Diagrama del modelo cinemático del robot A465.
El modelo cinemático es:
Los ángulos se obtienen mediante:
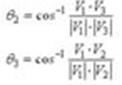 (Ec.12)
(Ec.12)
 (Ec.10)
(Ec.10)
El experimento consiste en calcular visual- mente los ángulos q2 (ángulo entre la base y la primera articulación del robot) q3 (ángulo entre la primera y la segunda articulación) que forman parte del modelo cinemático del robot.
Para obtener estos valores usamos las tres marcas visuales y el siguiente proceso:
1. Obtenemos el centroide (uL, vL) y (uR, vR) de las tres marcas
visuales.
2. Usando nuestro modelo óptico de visión estéreo obtenemos la posición correspon- diente (x,y,z), coordinada por los tres puntos visuales.
Estos valores se marcan como (P1,P2,P3).
3. Con esta información calculamos los valores
de los parámetros q2, q3 como sigue:
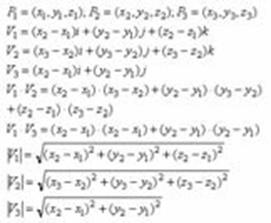
(Ec.11)
El experimento consiste en mover la segunda articulación del robot A465 (ver Figura 18 ) des- de -90º a 90º, y obtener usando la información visual el
ángulo q3 del robot A465.
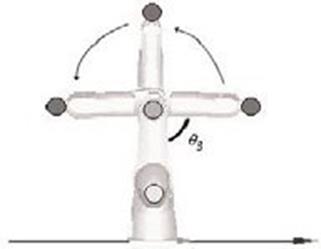
Figura 18. Experimento variando el ángulo q3 del robot A465
En la Tabla 3 se muestran los resultados, comparando la primera columna con la última, observamos que el error entre ambas es de tan sólo ±2º. Este
rango es aceptable para tareas que no requieran de alta precisión.
|
q
3
real
|
q
3
|
|
–90
|
–92.7840
|
|
–75
|
–76.7100
|
|
–60
|
–60.7780
|
|
–45
|
–45.6620
|
|
–30
|
–30.6810
|
|
–15
|
–15.7780
|
|
0
|
0.9057
|
|
15
|
13.8890
|
|
30
|
28.6460
|
|
45
|
43.4890
|
|
60
|
58.2490
|
|
75
|
72.7460
|
|
90
|
88.1120
|
Tabla
3. Resultados obtenidos con el modelo óptico de estéreo visión para diferentes ángulos de
q
3
.
CONCLUSIONES
La principal contribución consistió en el desa- rrollar e implementar un nuevo modelo óptico de estéreo visión, analizando los componentes ópticos del
sistema de visión por computadora. Este modelo se probó exitosamente en el robot A465, calculando los ángulos de su modelo cinemático. Nuestro modelo
puede usarse en diferentes aplicaciones de visión por computa- dora como por ejemplo, en control visual, en robots móviles para la reconstrucción en
tres dimensiones, etc.
AGRADECIMIENTOS
Agradecemos el apoyo brindado por el Labora- torio de Robótica de los Talleres y Laboratorios de la Escuela de Ingeniería de la Universidad La Salle, México.
REFERENCIAS
1. S.M. Seitz & C.R Dyer, Complete Scene Structure from Four Point Correspon- dences, Proc. 5th Int. Conf on Computer Vision, Cambridge
MA, EUA, pp. 330-337, 1995.
2. C.J Taylor & D.J. Kriegman, Structure and Motion from Line Segments in Multiple Images, IEEE Trans. on Pattern Analysis. Machine
Intelligence, núm. 17, vol. 11, 1995.
3. J.E.W. Mayhew & J.P Frisby, 3D Model Re- cognition from Stereoscopic Cues, MIT Press, 1991.
4. R. M. Haralick and L.G.Shapiro, Computer and Robot Vision II (Addison-Wesley Pub. Co., 1993).
5. E. Grosso, G.Metta, A.Oddera & G.Sandini, Robust Visual Servoing in 3-D Reaching Tasks, IEEE Trans. on Robotics and Automation, vol.
12, núm. 5, pp. 732-741, 1996.
6. S. B. Pollard, J. E. W. Mayhew and J. P. Frisby, A stereo correspondence algorithm using a disparity gradient limit, Perception,
14:449-470, 1985.
7. E. Trucco & A. Verri, Introductory Techni- ques for 3-Computer Vision, Prentice Hall, pp. 26-28, 1998.
8. R. Szeliski, From Image to Model (and Beyond): A Personal Restrospective, Vision Interface, núm 97, Kelowna, B.C, Mayo 21, 1997.
9. M. Chavarría, A. Soria & P. Wiederhold, Percepción monocular para el control de robots, Congreso Latinoamericano de Con- trol Automático, Guadalajara –México, D.F., 2002.
10. R. C. González y R. E. Woods, Tratamiento Digital de Imágenes, Addison Wesley / Díaz de Santos, 1996.
11. J. H. Sossa, Características Invariantes para el Reconocimiento de Formas en Visión por Computadora: una Panorámica. Instituto Politécnico
Nacional, Centro de Investigación en Computación, núm. 33, serie Azul, México, 1999.
12. E. Hecht y A. Zajac, Óptica, Colección Fondo Educativo Intermericano, 1977.
13. J. Denavit & R.S. Hartenberg, A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices, Journal of Applied Mechanics, pp.
215-221, 1955.
![]() 1
U. Ramon Llull, Departament d'Electrónica, Enginyeria i Arquitectura La Salle,
1
U. Ramon Llull, Departament d'Electrónica, Enginyeria i Arquitectura La Salle,




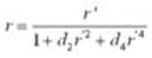
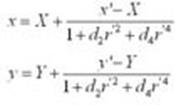




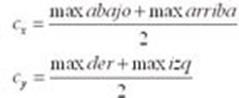



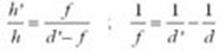

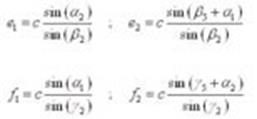
 f = 0.585091 cm d’= 1.704799 cm
f = 0.585091 cm d’= 1.704799 cm

 Así:
Así:


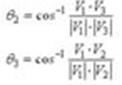 (Ec.12)
(Ec.12)
 (Ec.10)
(Ec.10)