Mejoras a un Algoritmo Genético Simple, aplicando conceptos de Computación Evolutiva

Claudia Hurtado González, Beatriz Izquierdo Rivera Marcela López Aguado Hernández, Armando Nicolás Cruz Eduardo Gómez Ramírez

Laboratorio de Investigación y Desarrollo de Tecnología Avanzada(LIDETEA) UNIVERSIDAD LA SALLE

E-mail: egr@ci.ulsa.mx

Recibido:Julio de 2002. Aceptado: Agosto de 2002

RESUMEN

Uno de los problemas con que se enfrentan los algoritmos evolutivos es la gran cantidad de tiempo que requieren para converger en la solución óptima. Por esta razón es muy importante el desarrollo de algorit- mos que mejoren su desempeño. En este artículo se presenta una versión mejorada de Algoritmo Genéti- co, así como la manera en que distintos parámetros internos, como mutación–número de padres afectan en la convergencia. Las pruebas propuestas se evaluaron estadísticamente, mediante un análisis de varianza. Esta metodología estadística de evaluación puede aplicarse para la sintonización

de cualquier Algoritmo Genético.

Palabras clave: Algoritmo evolutivo, algoritmo genético, padre adicional aleatorio, función memoria, con- tador estacionario, solución óptica, mutación, convergencia, análisis de varianza, sintonización.

ABSTRACT

The convergence time to the optimal solution is one of the most important problems of the evolutionary algorithms. This is the reason of the importance to develop new schemes that improve the performance of this kind of tools. A new version of Genetic Algorithm and a methodology to show the way internal para- meters such as mutation, number of parents, etc., correlated with the convergence are presented. The experiments were designed with a statistic methodology analysis of variance (ANOVA). This methodology can be applied with any similar GA. in order to tune its perfomance parameters.

Keywords: Evolutionary algorithm, genetic algorithm, add random parent, memory function, stable meter, optical solution, mutation, convergence, analysis of variance, tuning.

1. INTRODUCCIÓN

Hace algunos años todavía se hablaba de la dificultad para atacar problemas de tipo NP. Es decir, problemas cuya solución requería de una gran cantidad de pruebas y combinaciones, sin poder obtenerla con una solución analítica directa. Ejemplo de esto es el problema del agente viajero [1,2], cuya solución era intratable en términos de la computación tradicional. Esta dificultad no ha desaparecido pero sí se han incrementado las alternativas disponibles para resolver estos problemas. Por ejemplo, algorit-

mos como simulación de templado o recocido simulado (simulated annealing) [3] son alternati- vas ampliamente utilizadas para la solución de problemas como los mencionados anteriormen- te. Su principal problemática es que tienen una explosión combinatoria cuando se incrementa la cantidad de alternativas posibles. La com- putación evolutiva [4,5] ha propuesto importan- tes soluciones a este tipo de problemas. Inclu- sive en sitios WEB pueden encontrarse descrip- ciones muy interesantes a este respecto [6-12].

También ha habido una nueva tendencia a problemas de optimización utilizando teoría de juegos. Por ejemplo, en [13,14] puede revisarse una aplicación muy interesante en modelos de tráfico en comunicación móvil. A pesar de ser un importante recurso en el área de com- putación evolutiva y con una gran cantidad de aplicaciones desarrolladas, todavía no existen procedimientos formales, matemáticamente hablando, que permitan el análisis de estruc- turas con óptima convergencia. Es importante resaltar los esfuerzos que ha habido de varios autores [15-24] para demostrar la convergencia de diferentes propuestas de algoritmo genético en términos generales, es decir, convergencia a infinito, estabilidad, etc. Esto es, que aseguren una mejor convergencia que con técnicas de tipo aleatorio e, inclusive, que los parámetros utilizados internamente sean los óptimos para el propio algoritmo.

Este trabajo tiene como finalidad exponer algunas mejoras en el procedimiento para aplicar un Algoritmo Genético Simple, que per- mitan una mejor convergencia en términos de un menor número de individuos utilizados. Esto se traduce en menor tiempo de cómputo y por lo tanto en velocidad de respuesta del algoritmo. El punto de partida es el Algoritmo Genético (GA, por sus siglas en inglés) en su forma más sencilla, mismo que se fue modificando con el objetivo de mejorar su desempeño hasta llegar a la propuesta final, obteniendo, de esta mane- ra, tres versiones del algoritmo mejorado: Algo- ritmo Genético con Mutación, Algoritmo Genéti- co con Padre Adicional Aleatorio y Algoritmo Genético Propuesto. En cada una de las fases se realizó un estudio estadístico que permitió hacer un análisis del comportamiento del mode- lo en cuestión y así determinar la manera en que los cambios afectaban en el desempeño del algoritmo. Dicho estudio estadístico se realizó variando los parámetros que sintonizan el fun- cionamiento del algoritmo para determinar sus valores óptimos. La propuesta final de Algoritmo Genético comprende algunos conceptos que se exponen por primera vez como parte de la teoría de Algoritmos Genéticos.

2. METODOLOGÍA

El AG puede observarse como un proceso estocástico, al tener variables aleatorias como

condiciones iniciales, valores de probabilidad para la mutación o para algún otro tipo de pro- ceso. Es por eso que algunos autores han utilizado cadenas de Markov para modelar su comportamiento y hacer algunos estudios de convergencia (referencia); otros autores han utilizado otro tipo de estructuras, también estocásticas, para su estudio (referencia mía). En este caso se utilizará la metodología de diseño de experimentos (referencia Mont- gomery), en específico de análisis de varianza para estudiar su comportamiento.

2.1 Planeamiento del problema del número binario

A fin de probar las distintas versiones del mode- lo propuesto, se planteó un problema sencillo, cuyo objetivo es encontrar un número entero dentro del conjunto de los números naturales. Este problema se denominó como el problema del número binario y se detalla a continuación:

La meta es encontrar un número entero posi- tivo, N, que se genera de manera aleatoria en su forma decimal y posteriormente es conver- tido a su forma binaria. Debido a que se utiliza codificación binaria, el universo de búsqueda se acota por el número de genes que conforman a cada individuo. Por lo tanto, el universo de búsqueda se define como:

N Î U [0, 2 b - 1]

(Ec. 1)

donde: b es la dimensión del espacio solución.

La razón de utilizar distribución uniforme es que, por el momento, todo el rango de números tiene la misma probabilidad de seleccionarse. Los individuos de este universo son números enteros positivos, que se evalúan con la función objetivo planteada.

2.2 Metodología Estadística de Evaluación

Para el diseño del experimento se utilizó el enfoque de Análisis de Varianza (ANVAR) [25] para fundamentar los resultados. En específico, se utilizó el enfoque de k ejecuciones de un algoritmo para un mismo experimento. La muestra de k ejecuciones se denomina grupo.

El término de Análisis de Varianza surge de la manera en que este enfoque compara la varianza estimada de las medias de los grupos, contra la varianza de cada grupo. Cuando existe una clara separación entre las medias de cada grupo, la varianza es grande en comparación con la varianza de las medias. Esto se muestra en la siguiente figura.

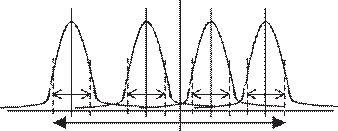
Figura 1. Análisis de varianza con clara sepa- ración en las medias

Por el contrario, cuando no existe una sepa- ración clara de las medias de cada grupo, la varianza es pequeña comparada con la varian- za entre las medias. Lo anterior se muestra en la siguiente figura.

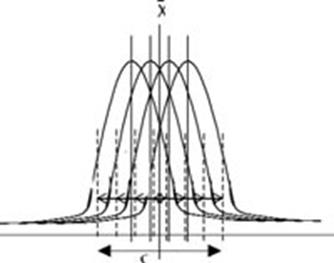
Figura 2. Análisis de varianza sin clara sepa- ración en las medias

Este enfoque utiliza conceptos muy intuitivos sobre el comportamiento de un sistema. Por ejemplo, supónganse distintos experimentos donde un solo parámetro es variado y se quiere saber el comportamiento o efecto de este parámetro en la respuesta. Para poder hacer una validación adecuada del comportamiento de la media del experimento para cada valor del parámetro, es necesario definir un número míni-

mo de ejecuciones. Sin una demostración ma- temática muy extensa, es posible entender que existe cierta relación proporcional entre el número de ejecuciones y la varianza obtenida para cada experimento.

En otras palabras, a menor varianza, existe mayor confiabilidad en los datos, ya que signifi- ca que éstos no están muy dispersos. Es nece- sario mencionar también, que un grado mayor de confiabilidad implica un mayor número de ejecuciones. De esta forma es posible obtener el número necesario de ejecuciones, en función de la varianza. Por otro lado, este número de ejecuciones también define un nivel de error permitido, obtenido a partir de la varianza de las medias. Estos dos parámetros, el nivel de con- fiabilidad y el nivel de error, son los que se uti- lizan como elementos para definir el número de ejecuciones. En la siguiente tabla se muestra la relación que existe entre el nivel de error y el nivel de confiabilidad [26].

Tabla 1. Tamaño de la muestra con respecto al nivel de confiabilidad y al nivel de error

	Error en Unidades de Varianza
Confiabilidad	0.05	0.06	0.07	0.08	0.09	0.10	0.11	0.12
0.99	2654	1844	1355	1037	820	664	549	461
0.98	2165	1504	1105	846	669	542	448	376
0.97	1884	1309	962	736	582	471	390	328
0.96	1688	1172	861	660	521	422	349	293
0.95	1537	1068	784	601	475	385	318	267
0.94	1415	983	722	553	437	354	293	246
0.93	1314	912	671	513	406	329	272	228
0.92	1226	852	626	479	379	307	254	213
0.91	1150	799	587	450	355	288	238	200
0.90	1083	752	553	423	335	271	224	188

Por ejemplo, un experimento que requiera u- na confiabilidad del 98% y un nivel de error del 0.1, necesita 542 ejecuciones.

Para el estudio estadístico realizado en la siguiente sección se tomaron los parámetros que se emplean normalmente en el diseño de experimentos, que son un error del 0.05 y una confiabilidad de 95%. Como puede observarse en la tabla 1, el número necesario de ejecucio- nes es de 1,537. En este caso se realizaron

1,540 ejecuciones. Con este valor puede asegu- rarse que las conclusiones sobre los experimen- tos tienen un alto nivel de confiabilidad y un error mínimo.

3. EXPLORACIÓN Y EXPLOTACIÓN

Cualquier algoritmo de optimización debe consi- derar dos técnicas para encontrar el objetivo buscado. La exploración busca nuevas áreas dentro del espacio de búsqueda, recabando información que, en una etapa posterior, será de utilidad. La explotación hace uso de la expe- riencia adquirida, ayudando a encontrar mejo- res soluciones.

Una búsqueda aleatoria es útil únicamente para llevar a cabo la exploración, mientras que un método heurístico aplica solamente la explotación.

Ambas técnicas deben aplicarse con un balance adecuado dentro de un AG, lo cual no es una tarea sencilla puesto que existe la posibi- lidad de que un gen influya de manera negativa en un individuo y puede llegar a ser dominante

4.1 Algoritmo Genético con Mutación

Es la primera versión del algoritmo propuesto en donde se aplicaron los conceptos de selección, recombinación y mutación.

El parámetro que determina la frecuencia con la cual se observará la mutación en algunos de los genes que conforman a los individuos se denominará, a partir de este momento, como Probabilidad de Mutación (PM) y se define como el valor utilizado en el algoritmo que indica si un gen determinado debe mutar o no. Se genera un número aleatorio (w) con distribución uniforme, comprendido entre 0 y 1:

w Î U [0,1]

(Ec. 2)

w se compara con la PM, si es inferior o igual a PM, entonces el gen mutará. Si denominamos Gi a cada gen de un individuo determinado, y a Gi un gen mutado, la mutación puede expre- sarse como:

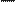en esa generación. Este fenómeno también se presenta en la naturaleza y se conoce como desviación genética. Para evitar una situación de este tipo dentro de un AG es necesario bus- car una probabilidad de mutación adecuada.

ìGi

í

îGi

w £ PM

w > PM

(Ec. 3)

4. RESULTADOS

Las dos primeras versiones del algoritmo pro- puesto, el Algoritmo Genético con Mutación y el Algoritmo con Padre Adicional Aleatorio, se de- sarrollaron en Matlab© por ser un lenguaje que permite un manejo sencillo de vectores y matri- ces. Mientras que la última versión, el Algoritmo Genético Propuesto, utiliza Microsoft Visual Ba- sic 5.0. Ambos lenguajes, presentan un tiempo de ejecución aceptable que permitió probar di- versos casos, respetando siempre el número de 1,540 ejecuciones por cada variación en los parámetros que sintonizan el algoritmo.

A continuación se presentan los resultados estadísticos obtenidos para cada uno de los algoritmos desarrollados.

Para todos los algoritmos aquí presentados la codificación es binaria y el criterio de selección es por rango. En el caso de la función objetivo se utilizó la función objetivo decimal, ya que el Algoritmo Genético con Mutación es el primer tipo de Algoritmo Genético con el que se realizaron estadísticas formales y análisis de sus resultados. La función objetivo decimal se define como el valor absoluto de la diferencia en su valor decimal del número buscado contra el número a evaluar.

La metodología del Algoritmo Genético con Mutación es la siguiente:

Paso 1. Generar de manera aleatoria la población inicial. Paso 2. Seleccionar los P mejores individuos para ser los padres de la generación. Paso 3. Recombinar a los padres con M punto(s) de cruce. Paso 4. Mutar: aplicar la probabilidad de mutación PM para cada hijo y determinar si debe mutar. Una vez que se determi- na que un hijo debe mutar, se aplica PM a cada uno de sus genes. Paso 5. Agregar los hijos que mutaron y los padres a la población de hijos generados. Paso 6. Evaluar a cada hijo de la nueva población con la función objetivo decimal. Paso 7. Regresar al paso 2.

uniforme. La gráfica 3 indica que los valores de PM comprendidos entre 8.5% y 9.5% son los más adecuados para el Algoritmo Genético con Mutación, porque para esos valores se obtiene un menor número de individuos generados; sin embargo, es importante mencionar que para la mayoría de los casos, el algoritmo terminó su ejecución al alcanzar el número máximo de generaciones.

Esto hace evidente que el algoritmo no con- vergió adecuadamente. La razón es que se uti- lizó una función objetivo que no explota las características de AG. Esto se puede explicar con el siguiente ejemplo. Supóngase la codifi- cación binaria de los siguientes números:

Como primer paso del estudio estadístico para este algoritmo se varió la probabilidad de mutación (PM) de 0.5% hasta 15%, con incre- mentos de 0.5%, fijando el resto de los pa- rámetros como sigue:

Parámetro	Valor
Número de Padres	2
Puntos de cruce	1
Población inicial	0.5%

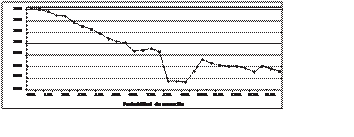
La figura 3 contiene un promedio del total de individuos que genera el Algoritmo Genético con Mutación para cada valor de PM. El prome- dio resulta después de 1,540 ejecuciones con un mismo valor de PM.

Figura 3. Algoritmo Genético con Mutación – Total de individuos contra PM

El número total de individuos es una métrica del desempeño del algoritmo, ya que indica la cantidad de números que fueron evaluados en cada ejecución y que debe ser menor a la canti- dad de números generados por una búsqueda secuencial y por una aleatoria con distribución

6310= 01111112

6410=10000002

La diferencia en decimal es de tan sólo 1 y su diferencia en binario, por ejemplo, utilizando distancia de Hamming es de 7. Este error es muy común en aplicaciones donde no se entiende la naturaleza del problema con respec- to a la función objetivo porque se evalúa única- mente al individuo, descartando la información que aporta cada gen en particular.

En estos casos es necesario utilizar otra fun- ción objetivo que considere la información de cada uno de los elementos del arreglo. Sin embargo, también se observó que a pesar de tener una función objetivo poco adecuada para el problema, es posible lograr la solución a un problema determinado por medio de un Algorit- mo Genético, ya que el Algoritmo Genético con Mutación llegó a encontrar el número solución, aunque no en la mayoría de los casos y no de la manera óptima.

El Algoritmo Genético con Mutación realiza una tarea de exploración más que de explota- ción dado que la función objetivo decimal no evalúa toda la información necesaria en cada individuo, es por ello que la solución al proble- ma del número binario se encontró únicamente en aproximadamente 10% del total de las ejecu- ciones realizadas. Es claro que si el número de generaciones o iteraciones no se hubiese limita- do, se habría encontrado la solución en todos

los casos, considerando que el AG funcionaba como una búsqueda aleatoria únicamente.

Esta sección solamente nos permitió enten- der un poco el funcionamiento de la función objetivo. En la siguiente sección se presentarán dos cambios; el de la función objetivo y otro nivel mutación mayor llamado padre adicional aleatorio.

4.2 Algoritmo Genético con Padre Adicional Aleatorio

La principal diferencia que tiene este algoritmo con respecto al Algoritmo Genético con Muta- ción es la introducción del Padre Adicional Alea- torio (PAA), que es un individuo generado de manera aleatoria, con distribución uniforme. El PAA se agrega al grupo de padres para la siguiente recombinación con la finalidad de dar mayor diversidad a la población generada.

Otra diferencia importante es que la mutación se aplica únicamente a los padres, para evitar que alguno de los hijos generados, que pudiera ser la solución del problema, se modifique y entonces se pierda.

Para esta versión del algoritmo se modificó la función objetivo decimal, convirtiéndose en una Función Objetivo Binaria. Esta función objetivo califica a los individuos de una población de acuerdo a su cercanía con el número binario buscado, sin perder de vista que lo más impor- tante es evaluar cuántos genes de cada indivi- duo tienen el valor correcto con respecto al número buscado. El individuo con un menor número de bits incorrectos es el más apto de la población actu

al.

El individuo con calificación de adaptación más baja es el mejor adaptado para el caso de la función objetivo binaria. Ésta es más comple- ja que la decimal, ya que requiere de 2 pasos. El primero es realizar una operación lógica de XOR entre el número buscado N y el individuo evaluado In:

T n = In Ä N

Tn será un número binario que contendrá tantos ceros como posiciones correctas tenga In con respecto a N. En el segundo paso, se determina la calificación de adaptación Cn, es el resultado de la suma de los valores de los bits que forman Tn.

La metodología del Algoritmo Genético con PAA es la siguiente:

Como primer paso del estudio estadístico para este algoritmo se varió la probabilidad de mutación. Se observó que el mejor compor- tamiento de este algoritmo se obtenía para valores de PM comprendidos entre 12% y 13%, por lo que este intervalo se amplió, haciendo variaciones de 0.1%. Esto se muestra en la figu- ra 4.

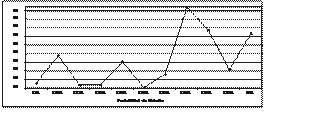
La figura 4 no muestra una tendencia clara cuando varía la probabilidad de mutación, ya que las variaciones en el número total de indivi- duos no son significativas con respecto al espa- cio total de búsqueda. Aún cuando la gráfica 4 muestra el mejor valor de PM en 12.5%, puede decirse que para el Algoritmo Genético con PAA valores de PM entre el 12% y el 12.5% son ade- cuados.

(Ec. 4)

mero total de individuos generados. Por otro la- do, el número de hijos obtenidos por genera- ción (I) está dado por la siguiente ecuación:

Figura 4. Algoritmo Genético con PAA -

I = (P + 1)R +1

(Ec. 5)

Total de individuos contra PM

Este algoritmo requiere de valores de PM altos ya que la mutación se aplica únicamente al grupo de padres, que es una población pequeña, con respecto al total de la población. Con valores bajos de PM, se observó que hay una tendencia a tener individuos repetidos constantemente, incrementando el riesgo de que el algoritmo llegue a un mínimo local.

Un mínimo local se define como el estado que se considera cuando un mismo individuo se repite como mejor padre en generaciones con- secutivas, sin alcanzar la solución óptima.

Por lo tanto, al incrementar la PM se generan menos individuos ya que existen más varia- ciones y se encuentra la solución más rápido.

En la figura 5 se muestra el comportamiento del número total de individuos promedio al modificar los puntos de cruce entre 1 y 2.

2949 1988

3500

3000

2500

2000

1500

1000

500

0

1 2

Puntos de cruce

Figura 5. Algoritmo Genético con PAA – Total de individuos contra número de puntos de cruce

La gráfica anterior muestra que, a mayor número de puntos de cruce menor será el nú-

Está ecuación es aplicable únicamente a

este algoritmo, ya que el número de padres al momento de la recombinación siempre será P+1 debido a la presencia del PAA.

La ecuación 5 nos dice que a mayor núme- ro de puntos de cruce (R), mayor será el número de individuos generados por iteración. Sin embargo, vemos en la figura 5 que para el total de individuos el resultado es el opuesto. Esto se explica a través de la función objetivo binaria, que evalúa correctamente a cada indivi- duo y selecciona como nuevos padres real- mente a los mejores números entre todos los generados en una población mayor, favorecien- do la convergencia del Algoritmo Genético con PAA.

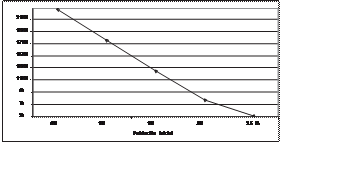
Para el caso del Algoritmo Genético con PAA, se estudió también el comportamiento al variar la población inicial de 0.5% a 2.5%, con incre- mentos de 0.5%. La figura 6 muestra el compor- tamiento del número de individuos obtenidos a partir de la primera recombinación, es decir, no toma en cuenta la población inicial ya que esto representa un incremento automático en el total de individuos generados por el algoritmo.

Como se observa en la figura 6, a mayor por- centaje de población inicial, menor será número de individuos generados durante la ejecución del algoritmo, ya que la población de la primera generación crece, obteniendo como primeros padres, individuos que son cada vez más cer- canos a la solución del problema. Mientras más grande sea la población inicial aleatoria, tam- bién será menor el número de generaciones que el algoritmo empleará para llegar a la solu- ción final. Sin embargo, no se recomienda tener poblaciones iniciales muy grandes, ya que esto reduciría la ejecución del Algoritmo Genético a una búsqueda semi-aleatoria.

permitió agregar mayor diversidad a la población bajo ciertas condiciones específicas. Primero, cuando el algoritmo llega a un mínimo local y cuando el mejor individuo de una genera- ción se repite. Finalmente la última aportación permite detener al algoritmo cuando se ha caído en un estado de mínimo local sin lograr salir del mismo.

Figura 6. Algoritmo Genético con PPA- Individuos generados contra población inicial

El Algoritmo Genético con PAA siempre re- suelve el problema del número binario, pero evalúa constantemente individuos ya evaluados previamente, por lo que se determinó que un mecanismo que elimine estos individuos repeti- dos favorecería el desempeño.

Por otro lado, el PAA es una forma de muta- ción de magnitud alta, que introduce súbita- mente gran diversidad a la población. En este modelo se insertó el PAA en cada generación, lo que incrementó el número total de individuos que, en promedio, genera el algoritmo; además de que en ocasiones evita que la ejecución llegue a un estado de mínimo local, pero en otras no aporta ningún tipo de mejoría, ya que el PAA es más lejano de la solución que los padres obtenidos en la última selección. De acuerdo con todo lo anterior, se determinó que el PAA sería utilizado únicamente cuando se detecte una situación de mínimo local, lo cual lleva a implantar un mecanismo que permita determi- nar que se ha llegado a un mínimo local.

Todas estas mejoras se desarrollan en el si- guiente modelo.

4.3 Algoritmo Genético Propuesto

Las principales diferencias de este algoritmo con respecto a la versión anterior son la inclusión de la función Memoria, uso del PAA de manera condicionada y la introducción del Con- tador Estacionario. La primera de estas adecua- ciones permitió que los individuos desechados no se consideraran nuevamente en generacio- nes subsecuentes. Esto permitió que el número de individuos obtenidos fuera menor que en las versiones anteriores; la segunda aportación

La metodología del Algoritmo Propuesta es la siguiente:

Para el estudio estadístico del algoritmo pro- puesto se analizaron variaciones en la probabili- dad de mutación (PM), en el número de padres, en el número de puntos de cruce y en la po- blación inicial. Además, estos análisis se enca- denaron, ya que después de determinar el me- jor valor de PM, éste fue utilizado para la deter- minación del número de padres, y así sucesiva- mente.

El primer paso para hacer la sintonización del Algoritmo Genético Propuesto fue determinar el valor para el contador estacionario, a través de la variación de la probabilidad de mutación (PM), desde 0.5% hasta 10%. Para cada valor de PM, el algoritmo se ejecutó 1,540 veces y se

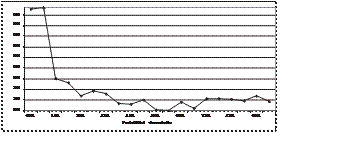
obtuvo el valor más alto alcanzado por el conta- dor estacionario, mismo que se determinó en 670 para las corridas subsecuentes. Estos valo- res se muestran en la figura 7.

Figura 7. Valores máximos del contador estacionario

Al variar la Probabilidad de Mutación de 0.5% a 10% con incrementos de 0.5% se encontró que el valor con el cual se generan el menor número de individuos fluctuaba entre 5% y 6.5%, por lo que al hacer un mayor ajuste entre estos valores, se encontró que el valor era 6.2%.

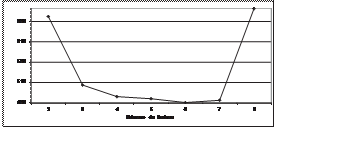
El número de padres varió entre 2 y 8. Es importante ver que, aún cuando a mayor núme- ro de padres el Algoritmo Genético Propuesto genera un mayor número de individuos por generación, el número total de individuos promedio es menor. Esto quiere decir que la diversidad obtenida a partir de la recombinación favorece una solución en términos de velocidad para el problema del número binario. Esto se debe a que el algoritmo hace un uso efectivo de la explotación de información. La función me- moria puede influir también en este sentido, ya que siempre se recombinan individuos diferen- tes y mejores con respecto a la generación an- terior. Los resultados se muestran en la figura 8.

Figura 8. Algoritmo Genético Propuesto – Total de individuos contra número de padres

Para entender la figura 8 es necesario consi- derar que a mayor número de padres se pro- duce una mayor descendencia, por lo tanto se elimina un mayor número de individuos y la probabilidad de que un nuevo individuo se encuentre en el universo de los elementos elimi- nados es mayor. Esto da como resultado que el número de individuos evaluados y considerados en la contabilización total de individuos es menor conforme el número de padres aumenta. Sin embargo, es necesario tener en cuenta que un número excesivo de padres podría ocasionar resultados contrarios a los esperados, tal como sucedió en los ensayos con 8 padres.

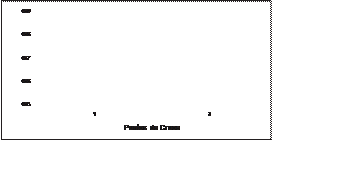
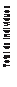A mayor número de puntos de cruce se gene- ra un mayor número de individuos. Si el número de puntos de cruce incrementa, el número de individuos obtenidos por generación aumentará, además de que también se incrementa la posi- bilidad de obtener individuos repetidos, lo cual es compensado con la acción de la función me- moria, que los elimina. Estos resultados se ob- servan en la figura 9.

468
466

Figura 9. Algoritmo Genético Propuesto –

Total de individuos contra número de puntos de cruce

Debido a la variación de individuos casi des- preciable se determinó el uso indistinto en los puntos de cruce.

La población inicial fue variada entre 0.5% y 5%, con incrementos del 0.5%. Conforme au- menta la población inicial, el número total de individuos aumenta. Por cada incremento en la población inicial se producen aproximadamente 328 individuos más, que corresponden al incre- mento de 0.5% de 65536. Es por ello que la grá- fica de la figura 10 muestra los valores que co- rresponden a los individuos que se generaron a partir de la recombinación y mutación, es decir,

corresponde a la resta del total de individuos generados menos la población inicial. Graficar los datos de esta manera permite hacer un estu- dio más objetivo del comportamiento del algorit mo con respecto a los incrementos de la pobla- ción inicial.

Figura 10. Algoritmo Genético Propuesto – Individuos generados contra población inicial

De acuerdo con la gráfica anterior, el número de individuos generados decrece conforme se incrementa la población inicial, lo cual es un resultado esperado, ya que a mayor población inicial hay una mayor posibilidad de tener mejo- res individuos para ser los padres elegidos para la primera recombinación. Esto significa que los padres estarán cada vez más cerca de la solu- ción, mientras más individuos se obtengan en la población inicial.

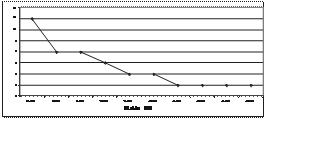
En cuanto al comportamiento del número de generaciones, éste tiende a reducirse a mayor población inicial, como se muestra en la figura 11.

Haciendo una análisis conjunto de las gráfi- cas 10 y 11, se observa que aún cuando hay disminuciones de hasta 100 individuos al incre- mentar la población inicial, el número de gene- raciones no mejora significativamente. Por otro lado, es importante mencionar que el tiempo de ejecución del algoritmo incrementa considera- blemente conforme se aumenta el porcentaje de la población inicial. Por esta razón, es recomen- dable utilizar un porcentaje pequeño para la po- blación inicial, entre el 0.5% y el 1.5%, para no incrementar excesivamente el total de individuos generados, así como para tener tiempos de ejecución aceptables.

De manera general, el Algoritmo Genético Propuesto alcanza la solución al problema con menor número de individuos generados y con menor número de generaciones, si se com- para con las versiones anteriores. Debido al uso de la función memoria, se optimiza el proceso de evaluación y de selección.

Otro aspecto importante que contempla el modelo propuesto es que realiza, de manera equilibrada, la exploración y la explotación de la información que va obteniendo a lo largo de la ejecución. Se recurre a la explotación al momento de evaluar y determinar a los mejores individuos tratando de encontrar la solución. Sin embargo, cuando se llega al estado de mínimo local, se hace uso de la exploración para inser- tar diversidad, a través del padre adicional alea- torio con la finalidad de superar dicho estado.

Por otra parte, el Contador Estacionario es el

llega a un mínimo local y, por lo tanto, regula el uso de los padres adicionales aleatorios. Por otro lado, marca una nueva condición de termi- nación que evita procesamiento inútil cuando el

Figura 11. Algoritmo Genético Propuesto – Número de generaciones contra población inicial

El número de generaciones se reduce con- forme aumenta la población inicial, con variacio- nes máximas de 3 generaciones por cada incre- mento de población inicial. También es impor- tante mencionar que incrementar la población inicial arriba del 3.5% no reporta ningún tipo de mejoría, ya que el número de generaciones no desciende más allá de 5.

aceptable de generaciones. Dependiendo de la naturaleza del problema es posible considerar, en varios casos, que el mínimo local alcanzado es igual al global dentro del espacio solución, o al menos está muy cerca de la solución.

5. DISCUSIÓN

Una manera sencilla de calificar el desempeño de un Algoritmo Genético es comparar sus resultados contra búsquedas aleatorias con dis- tribución uniforme y contra búsquedas secuen- ciales, las cuales no requieren de mucha complejidad para su desarrollo; sin embargo, pueden llegar a consumir amplios períodos de procesamiento, ya que son poco eficientes.

Los tres algoritmos presentados anteriormen- te se comparan contra 1540 ejecuciones de una búsqueda secuencial que resuelve el problema del número binario, así como contra 1540 ejecu- ciones de una búsqueda aleatoria con distribu- ción uniforme para llegar al número buscado. Los resultados muestran el número total de indi- viduos generados, ya que es la principal métrica de desempeño en un Algoritmo Genético.

Los parámetros considerados para el Algorit-

observamos en la figura 13 que el Algoritmo Genético Propuesto genera el menor número total de individuos. El Algoritmo Genético con Padre Adicional Aleatorio genera un mayor nú- mero de individuos que el Algoritmo Genético con Mutación, no obstante, esto es lógico por dos motivos principales. El primero es que siempre se tiene un número de padres mayor aún cuando el número predeterminado sea de dos, ya que la inclusión del padre adicional aleatorio siempre lo incrementa en uno. El segundo motivo es el hecho de saber que el Algoritmo Genético con Mutación, en la mayoría de los casos, no encuentra la solución al proble- ma, por lo que la comparación no es totalmente válida con los datos actuales.

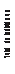co con PAA y el Algoritmo Genético Propuesto fueron los siguientes:

Probabilidad de mutación	1%
Número de padres	2
Población inicial	0.5%

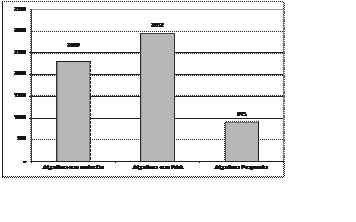
La figura 12 muestra los resultados logrados, donde se observa que siempre se obtendrán mejores resultados con un Algoritmo Genético que con una búsqueda secuencial o aleatoria con distribución uniforme.

70000

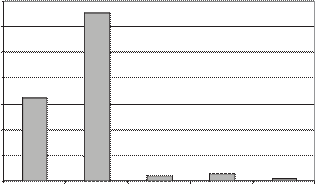
Figura 13. Número total de Individuos promedio por tipo de algoritmo

Para hacer posible la comparación del Algo- ritmo Genético con Mutación contra una bús- queda secuencial, una búsqueda aleatoria con distribución uniforme o contra cualquier otro

60000

50000

65917

modelo, sería necesario eliminar la condición

de terminación que marca el máximo de gene- raciones permitido.

40000

30000

20000

10000

0

32677

2299 2952 915

Es importante observar que el Algoritmo Genético Propuesto genera en promedio 915 individuos para los parámetros propuestos al principio de esta sección. Este número de indivi- duos representa el 1.39% del espacio total de

Búsqueda secuencial

Búsqueda Aleatoria

Algortimo con mutación

Algoritmo con PAA

Algoritmo Propuesto

búsqueda y donde el 0.5% corresponde a la

población inicial aleatoria, por lo que muestra

Figura 12. Número total de Individuos promedio

por tipo de algoritmo, incluyendo búsquedas secuencial y aleatoria

Haciendo el mismo tipo de comparación, úni- camente entre los tres modelos presentados,

un alto desempeño, ya que encuentra la solu- ción explorando únicamente el 0.89% del espa- cio total de búsqueda, en este caso, de 65,536 números.

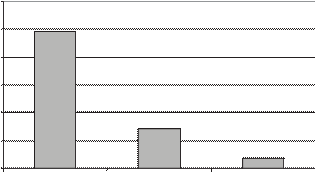
Al observar el número de generaciones ob- tenido en cada uno de los modelos estudiados, vemos que va decreciendo conforme el algorit- mo se mejoró.

1200

987

El estudio estadístico mostró que las modifi- caciones realizadas al algoritmo en realidad aportaron mejoras, porque se observó una dis- minución en el número total de individuos y en el número total de generaciones. Por su parte, el algoritmo propuesto tuvo un impacto positivo en la velocidad de convergencia. Aún cuando todos los experimentos realizados tuvieron un

1000

800

600

400

0

291

76

Algor timo con mutación Algoritmo con PAA Algoritmo Propuesto

universo de búsqueda de 65,536 individuos, se observó una tendencia a favorecer la velocidad de convergencia cuando el espacio de búsque- da sea mayor, ya que hay una relación expo- nencial.

El planteamiento de un problema de solución conocida, el problema del número binario, fue

Figura 14. Número de generaciones promedio por tipo de algoritmo

Como se ve en la figura 14, el Algoritmo Genético Propuesto tiene una drástica caída con respecto al Algoritmo Genético con PAA, lo cual nos indica que los mecanismos que se agregaron en esta versión contribuyen a mejo- rar su desempeño. También es necesario men- cionar que a partir del momento en que se cambió la función objetivo decimal a función objetivo binaria, el Algoritmo Genético desarro- llado siempre resolvió el problema del número binario.

6. CONCLUSIONES

Partiendo de un Algoritmo Genético Simple se generó un modelo nuevo de Algoritmo Genético, donde se incluyeron los conceptos que fueron desarrollados a lo largo de este trabajo: Padre Adicional Aleatorio, Función Memoria y Conta- dor Estacionario.

La introducción del Padre Adicional Aleatorio produce una mutación de alta magnitud, que se aplica únicamente cuando el algoritmo ha llega- do a un mínimo local. La Función Memoria se utiliza para evitar la evaluación de individuos uti- lizados anteriormente. La Función Memoria además ayuda a minimizar el número total de individuos generados. Por último, el Contador Estacionario es un parámetro que regula la uti- lización del Padre Adicional Aleatorio cada vez que el algoritmo ha alcanzado un mínimo local y es una condición de salida adicional para evitar procesamiento innecesario.

útil por un lado para la compresión de los con- ceptos de recombinación, mutación, evaluación y selección. Por otro lado, facilitó el desarrollo de la metodología de sintonización, que poste- riormente puede aplicarse a cualquier otro pro- blema resuelto por medio de Algoritmo Genéti- co.

El Algoritmo Genético con Mutación aplica dos tipos de mutación a los hijos, la primera se aplica para decidir si el individuo muta o no y la segunda se realiza al nivel de genes aplicando el mismo procedimiento. En este algoritmo, las estadísticas muestran que la convergencia va mucho más allá del máximo de generaciones que se definió, siendo esto un resultado basado en la exploración y derivado de la función objeti- vo decimal incorrecta.

En el segundo algoritmo propuesto, Algoritmo Genético con Padre Adicional Aleatorio, se a- porta el primer concepto, introduciendo el Padre Adicional Aleatorio para la creación de hijos por medio de la recombinación, mutación de los padres y la selección de los mejores individuos para la nueva generación. De esta forma, el número de individuos se incrementa en cada generación debido al Padre Adicional Aleatorio. Cabe mencionar que este algoritmo converge en un número de generaciones menor a mil, debido a que la función objetivo fue redefinida como binaria, la cual evalúa al individuo toman- do en cuenta la aportación de la información contenida en cada uno de sus genes, es decir, la función objetivo binaria refleja correctamente la naturaleza del problema.

En el algoritmo final se aplican, adicional- mente, la Función Memoria y el Contador Esta- cionario. Los resultados de estos nuevos con- ceptos, propuestos arrojan una mejoría notable en la disminución de la cantidad de individuos y de generaciones. La Función Memoria evita la evaluación innecesaria de individuos al com- parar cada elemento de la nueva generación con los individuos descartados, reduciendo el número total de individuos. El Contador Esta- cionario, por su parte, determina el momento de introducir un Padre Adicional Aleatorio cuando el algoritmo ha llegado a un mínimo local. Si el algoritmo no supera este estado a través de la introducción de Padres Adicionales Aleatorios sucesivos, el Contador Estacionario también permite terminar la ejecución del algoritmo, sin haber alcanzado la solución, con el fin de evitar un procesamiento innecesario.

Como trabajo futuro se puede tomar el algo- ritmo propuesto para aplicarlo en un problema real, en donde se compruebe si los parámetros definidos y la estructura en general son apropia- dos para la solución de un problema en particu- lar. La sintonización de un Algoritmo Genético varía en función de las características del pro- blema a resolver. Por ejemplo, un problema con mayor riesgo de caer en mínimos locales proba- blemente requiera la introducción de más de un Padre Adicional Aleatorio.

Una mejora a este algoritmo es utilizar más la explotación por medio de un ajuste fino cuando el Contador Estacionario se active y el mejor individuo se encuentre a una determinada dis- tancia del óptimo global. Para este tipo de situa- ciones, este mecanismo deberá sustituir la intro- ducción del Padre Adicional Aleatorio.

El futuro de la Computación Inteligente es uti- lizar un sistema híbrido para la solución de pro- blemas, un trabajo posterior interesante sería realizar un Algoritmo Genético en combinación con otro de los paradigmas, Lógica Difusa o Redes Neuronales Artificiales. El tipo de combi- nación o de sistema híbrido que se vaya a realizar dependerá del problema en cuestión.

Finalmente, una aportación muy importante de este trabajo es la explicación clara de los pasos utilizados para realizar la sintonización del algoritmo propuesto.

7. REFERENCIAS

1. Baskaran, G., Fu, Y. & Anderson, P. W., On The Statistical Mechanics of the Traveling Salesman Problem. Journal of Statistical Physics, núm. 45, pp. 1-25, 1986.

2. Kirkpatrick, S. & Toulouse, G., Configura- tion Space Analysis Of Traveling Salesman Problems. Journal de Physique, núm. 46, pp. 1277-1292, 1985.

3. Kirkpatrick, S., Gelatt (Jr.), C. D. & Vecchi,

M. P., Optimization by Simulated Annealing.

Science, núm. 220, pp. 671-680, 1983.

4. Bäck Thomas, Fogel David, Michalewicz Zbigniew, Handbook of Evolutionary Com- putation, The Institute of Physics Publish- ing, 1998-2000.

5. Vázquez Nava, A. & Figueroa Nazuno J., Algoritmo Genético: un método eficiente para problemas de optimización. XXXIV Congreso Nacional de Física. México, DF, 21-25 de octubre, 1991.

6. Obitko, Marek, Genetic Algorithms, http://cs.felk.cvut.cz/~xobitko/ga/main.html, 1998.

7. European Network Of Excellence On Evo- lutionary Computation (EvoNet), Flying Cir- cus–Genetic Programming, http://www.cs.- vu.nl/ci/Flying_Circus/, noviembre de 1997.

8. Beasly David, The Hitch-Hicker’s Guide to EvolutionaryComputation,http://surf.de.uu. net/research/softcomp/EC /FAQ/part2, sep- tiembre de 2000.

9. Fernández Jaime, The GP Tutorial,-

http://www.geneticprogramming.com-

/Tutorial/index.html, julio de 1985.

10. Genetic Programming, Inc., Genetic Pro- gramming Tutorial,http://www.genetic-pro- gramming.com/gpanimatedtutorial.html, octubre de 1999.

11. Merelo Guervós,J. J., Informática Evoluti- va: Algoritmos Genéticos,http://geneura.- ugr.es/~jmerelo/ie/ags.htm,GeNeura Departamento de Arquitectura y Tecnología de los Computadores de la Universidad de Granada, mayo de 1997.

12. Andina de la Fuente, Diego, Tutorial de la Universidad Politécnica de Madrid (UPM), http://www.gc.ssr.upm. es/inves/ann2/con- cepts/biotype.html, España, enero de 2001.