Cellular Neural Networks Learning using Genetic Algorithm

Eduardo Gómez Ramírez, Ferran Mazzanti* & Xavier Vilasis Cardona* Laboratorio de Investigación y Desarrollo de Tecnología Avanzada (LIDETEA) UNIVERSIDAD LA SALLE

E-mail: egr@ci.ulsa.mx

*Departament d'Electrónica, Enginyeria i Arquitectura La Salle, U. Ramon Llull, Pg. Bonanova 8, 08022 Barcelona, España

E-mail: mazzanti@salleURL.edu xvilasis@salleURL.edu

Recibido: Julio de 2002. Aceptado: Agosto de 200

ABSTRACT

In this paper an alternative to CNN learning using Genetic Algorithm is presented. The results show that it is possible to find different solutions for the cloning templates that fulfill the same objective condition. Different examples for image processing show the result of the proposed algorithm.

Keyword: Cellular neural network, learning, genetic algorithm, cloning templates, image processing.

RESUMEN

En este trabajo se propone una alternativa para el aprendizaje de Redes Neuronales Celulares utilizando algoritmo genético. Con las simulaciones realizadas se observó que es posible encontrar diferentes com- binaciones de matrices de pesos con las que se obtienen los mismos resultados. Se muestran diferentes ejemplos para el procesamiento de imágenes para representar el comportamiento del algoritmo.

Palabras clave: Redes neuronales celulares, aprendizaje, algoritmo genético, plantilla donadora, proce- samiento de imagen.

INTRODUCTION

Cellular Neural Networks (CNNs)1 are arrays of dynamical artificial neurons (cells) locally inter- connected. This essential characteristic has ma- de possible the hardware implementation of lar- ge networks on a single VLSI chip2 and optical

1 O. Chua & L. Yang: "Cellular Neural Networks: Theory",

IEEE Trans. Circuits Syst., vol. 35, pp. 1257-1272, 1988.

O. Chua & L. Yang: "Cellular Neural Networks: Applica- tions", IEEE Trans. Circuits Syst., vol. 35, pp.1273-1290, 1988.

2 Liñan, L., Espejo, S., Dominguez-Castro, R., Rodriguez- Vazquez, A. ACE4K: an analog VO 64x64 visual micro- processor chip with 7-bit analog accuracy. Int. J. of Circ. Theory and Appl. en prensa, 2002.

Kananen, A., Paasio, A. Laiho, M., Halonen, K. CNN appli- cations from the hardware point of view: video sequence segmentation. Int. J. of Circ. Theory and Appl. en prensa, 2002.

computers.3 The particular distribution of neu- rons in two–dimensional grids has turned CNNs into a particularly suitable tool for image pro- cessing.

Determining the correct set of weights for CNNs is traditionally a difficult task. This is, essentially, because gradient descent methods get rapidly stuck into local minima.4 One finally resorts either to template the library, or sophisti-

3 Mayol W, Gómez E.: "2D Sparse Distributed Memory- Optical Neural Network for Pattern Recognition". IEEE International Conference on Neural Networks, Orlando, Florida, 28 de junio a 2 de julio, 1994

4 M. Balsi, "Hardware Supervised Learning for Cellular an Hopfield Neural Networks", Proc. of World Congress on Neural Networks, San Diego, Calif, 4 al 9 de junio, pp. III, 451-456, 1994.

cated elaborations requiring a deep insight of the CNN behavior.5 Among global optimization methods for learning, Genetic Algorithms reveal to be a popular choice6. However, authors usua- lly show a genetic algorithm to find only one of

A. Mathematical Model

The simplified mathematical model that defines this array8 is the following:

dx c

the matrixes. The authors Doan, Halgamuge et = - xc (t ) +

a c y d (t ) +

b c u d + ic

al 7 solely show experiments for specific cases dt

å d å d

and possibly the examples presented only work with these constraints that, of course, reduce the space solution.

d ÎN r ( c )

d ÎN r ( c )

(Eq.1)

In this work a genetic algorithm approach is developed to compute all the parameters of a Cellular Neural Network (weights and current).

y c (t ) = 1 (xc (t ) + 1 - xc (t ) - 1))

2

(Eq.2)

The results show that it is possible to find many different matrixes that fulfill the objective condi- tion. Different examples of image processing are presented to illustrate the procedure developed.

The structure of the paper is the following: Section 2 describes the theory of Cellular Neural Networks, Section 3 the genetic algorithm pro- posed and in Section 4 the way the algorithm was applied to find the optimal parameters for image processing.

CELLULAR NEURAL NETWORKS

As it was defined on its origins, a CNN is an identical array of non-linear dynamic circuits. This array could be made of different types depending on the way they are connected or the class of the neighborhood.

where xc represents the state of the cell c, yc the

output and uc its input. The state of each cell is controlled by the inputs and outputs of the adja- cent cells inside the r-neighborhood Nr(c). The outputs are feedback and multiplied by acd and the inputs are multiplied by control parameters bcd. This is the reason that acd is called retro and bcd is called control. The value ic is constant and is used for adjusting the threshold 9. These coef- ficients are invariants to translations and it would be called cloning template.

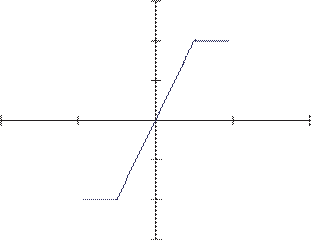
The output yc is obtained applying the equa- tion (2). This equation limits the value of the out- put on the range between [-1,1], in the same way the activation function does in the classical ANN models (Fig. 1).

1.5 y

5 Zarandy, A., The Art of CNN Template Design. Int. J. of Circ. Th. Appl., pp. 5-23, 1999.

6 Kozek, T., Roska, T., Chua, L.O. Genetic Algorithm for CNN Template Learning. IEEE Trans. Circ. Syst., pp. 392- 402, 1993.

P. López, M. Balsi, D.L. Vilario, D. Cabello, Design and Training of Multilayer Discrete Time Cellular Neural Net- works for Antipersonnel Mine Detection using Genetic Algorithms, Proc. of Sixth IEEE International Workshop on Cellular Neural Networks and their Applications, Cata- nia, Italia, 23 al 25 de mayo, 2000.

Taraglio S. & Zanela A., Cellular Neural Networks: age- netic algorithm for parameters optimization in artificial vision applications, CNNA-96., Proceedings, Fourth IEEE International Workshop, pp. 315-320, 24 al 26 de junio,

Sevilla, España, 1996.

7 Doan, M. D., Halgamuge, S., Glesner M. & Braunsforth, Application of Fuzzy, GA and Hybrid Methods to CNN Template Learning, CNNA-96, Proceedings, Fourth IEEE International Workshop, pp. 327-332, 24 al 26 de junio, Sevilla, España, 1996.

1

0.5

0

-4 -2 0 2 4

-0.5

-1

-1.5

Figure 1. Output function

8 Harrer H. & Nossek J.: "Discrete-Time Cellular Neural Net- works". Cellular Neural Networks. Editado por T. Roska &

J. Vandewalle. John Wiley & Sons, 1993.

9 This coefficient is equivalent to the input bias on other arti- ficial neural networks.

B. Discrete Mathematical Model

The mathematical model illustrated before could be represented by the following expression:

c

problem with the use of gradient error techni- ques, as in these cases, it is not possible to find an optimal solution. One alternative is the use of evolutionary computation techniques that can be applied to find the different solutions or alter-

dx

dt

where:

k c =

= - xc( t ) + k c

a c y d ( t ) +

(Eq.3)

b c u d + ic

natives to the same problem.

The next section describes the methodology of Genetic Algorithm used in this work.

å d

d ÎNr ( c )

å d

d ÎN r ( c )

GENETIC ALGORITHM

Because the final state is obtained evaluating x(¥), the model could be simplified as:

Genetic Algorithm (GA) is a knowledge model inspired on some of the evolution mechanisms observed in nature. GA usually follows the next

x c (k ) =

å ac yd (k ) +

å bcud + ic

cycle 11: (Fig. 2)

d

d

d ÎN r ( c )

d ÎNr (c )

(Eq. 4)

• Generation of an initial population in a ran- dom way.

• Evaluation of the fitness or some objective

Some authors also considered a modification

to the output (eq. 2), as follows [4]:

function of every individual that belongs to the population.

• Creation of a new population by the execu-

y c (k ) =

f ( xc ( k - 1))

tion of operations, like crossover and muta- tion, over individuals whose fitness or profit

ì 1

y c (k ) = í

î- 1

si x c (k - 1) > 0

si x c (k - 1) < 0

(Eq. 5)

value have been measured.

• Elimination of the former population and ite- ration using the new one until the termination criteria is fulfilled or it has reached a certain

However, the simplification made (eq. 4) could be used with the function of the eq. 2.10 [1]. Equation (4) can be represented using the convolution operator like:

X k = A*Yk + B *Uk + I

(Eq. 6)

where matrix A and B correspond to the rotation of 180º of the corresponding coefficients acd and bcd . The previous step is not necessary if the matrix has the property of A=AT.

The cloning template, in some cases, is a set of different combinations that fulfill the same conditions, e.g., there are different matrixes that can solve the same problem. This can be a

10 M. Alencastre-Miranda, A. Flores-Méndez & E. Gómez Ramírez: "Comparación entre Métodos Clásicos y Redes neuronales celulares para el análisis de imágenes". XXXVIII Congreso Nacional de Física. Zacatecas, Zaca- tecas, México, 16 al 20 de octubre, 1995.

number of generations.

In this work the crossover or sexual recombi- nation, the mutation and other special process that we call ‘add parents’12 and ‘add random parents’ are used. Next Sections describe these processes.

Figure 2. Operators of Genetic Algorithm

11 Alander J. T., An Indexed Bibliography of Genetic Algo- rithms: Years 1957, 1993, 1994, Art of CAD Ltd. Bedner I., Genetic Algorithms and Genetic Programming at Stan- ford, Stanford Bookstore, 1997.

12 E. Gómez-Ramírez, A. Poznyak, A. González Yunes & M. Avila-Alvarez. Adaptive Architecture of Polynomial Artifi- cial Neural Network to Forecast Nonlinear Time Series. CEC99 Special Session on Time Series Prediction. Hotel Mayflower, Washington D.C., EUA, 6 al 9 de julio, 1999.

A. Crossover

éM1 ù

The crossover operator is characterized by the

F g = ê

M

ë

ú, M 1 = [a

2 û

b ], M 2 = [c d ]

combination of the genetic material of the indivi-

duals that are selected in function of the good

Example:

é[a

ê

b ]¬ù

ú

performance (objective function).

C (Fg

)= ê[a d ] ú

ë

û

ê[c b] ú

To explain the multipoint crossover for each fixed number g=1,..,ng, where ng is the number

ê[c

d ]¬ú

of total generations, let introduce the matrix Fg which is the set of parents of a given population. This matrix is Boolean of dimension, Fg: npxnb, where np is the number of parents of the popula- tion at the generation g and nb is the size of every array (chromosomes). Let C(Fg,nt) be the crossover operator which can be defined as the combination between the information of the parents set considering the number of intervals nt of each individual and the number of sons ns such that:

s p

n = n nt

(Eq. 7)

Note that with this operator the parents Fg of

the population g are included in the result of the crossover.

For the problem of CNN learning every sec- tion of one father can be represented by one column or one row of one matrix of the cloning template (matrix acd and bcd ).

B. Mutation

The mutation operator just changes some bits that were selected in a random way from a fixed probability factor Pm; in other words, we just vary the components of some genes. This ope- rator is extremely important, as it assures the maintenance of the diversity inside the popula-

tion, which is basic for the evolution. This opera-

Then C(Fg,nt):npxnb -7 nsxnb. To show how

the crossover operator can be applied the follo-

tor M :nsxnb

-7 nsxnb

changes with probability

wing example is introduced. Let Fg has np=2 and

n t =2. This means that the array (the information

P m a specific population in the following way:

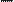of one father) is divided in 3 sections and every

M F , P

ìFij

r (w) £ Pm

section is determined with ai and bi respectively

( ij

m )= í

F ij

r (w) > Pm

for i=1,..,nt. It's important to appoint that with this operator the parents Fg of the population g are included in the result of the crossover:

î

C. Add Parents Mutated

(Eq. 8)

In this part the parents Fg are mutated and added to the result of the crossover process, then the population Ag at the generation g can be obtained like:

é C(Fg ) ù

A g = êM (F , P )ú

ë g m û

(Eq. 9)

Figure 3. Multipoint Crossover Operator

This step and the previous one ensure the convergence of the algorithm, because every generation at least has the best individual obtained in the process. With this step the origi- nal and mutated parents are included in the

generation g and with some probability the indi- viduals tend to the optimal one.

D. Selection Process

The Selection Process Sg computes the objec- tive function Og that represents a specific crite- rion to maximize or minimize and selects the best np individuals of Ag as:

of the matrix. In the current case only mutations are used.

APPLICATION IN IMAGE PROCESSING

The procedure used to train the network was:

1. To generate the input patterns using a known matrix in image processing to find the different kind of lines (horizontal, verti-

n p

S g (Ag , np )= min

O g (Ag )

(Eq. 10)

cal, diagonal) in different images.

2. To train the network using the methodology explained above using GA.

3. Test the results using a new pattern.

Then, the parents of the next generation can be calculated by:

F g +1 = Sg (Ag , np )

(Eq. 11)

Summarizing, the Genetic Algorithm can be describe with the following steps:

1. For the initial condition g=0 select the A0 in a random way, such that A0 : nsxnb

2. Compute F1= S0(A0)

3. Obtain Ag

4. Calculate Sg

The results were repeated to obtain different templates for the same problem. The parame- ters used are: 4,000 individuals in the initial population and 5 parents. The change in the values for every coefficient was evaluated using an increment of 0.125 to reduce the space solu- tion.

Example 1 Horizontal Line Detector

Figures 4 and 5 show the input and output pa- tterns used. This pattern was obtained using a well known matrix:

5. Return to step 3 until the maximum number of generations is reached or one of the indivi- duals of Sg obtains the minimal desired value of Og

é0

M = ê0

ê

êë0

-1 0ù

2 0ú

ú

-1 0úû

E. Add Random Parents

To avoid local minimal a new scheme is intro- duced and it is called ‘add random parents’. If the best individual of one generation is the same

The parameters obtained are: First Simulation:

é- 0.125 0 0 ù

than the previous one, a new random individual is included like parent of the next generation. This step increases the population because when crossover is applied with the new random parent, the number of sons increases. This step is tantamount to have a major mutation probabil-

A = ê 0

ê

êë - 0.75

2.5

- 1.375

0.125ú

ú

0.125úû

ity and to search in a new generation points of the solution space.

é- 0.125

B = ê 0.375

ê

- 2 0 ù

2.75 0 ú

ú

To apply the previous theory of GA, every individual is the corresponding matrix A (acd) and B (bcd). The crossover is computed using every column of the matrix like previous explanations and the mutation is applied to every component

êë 0.375

- 0.875

I=-2.875

- 0.25úû

Input Output

Second Simulation

é 4.5

- 2.25

- 0.5 ù

A = ê- 1.625

ê

êë 2.125

0.75

- 0.875

3.375 ú

ú

- 0.875úû

é 0.75

- 7.125

- 0.625ù

B = ê 2.625

ê

- 0.875

2.25 ú

ú

êë- 3.125

- 0.875

I=0.625

2.375 úû

Example 2 Vertical Line Detector

Figures 6 and 7 show the input and output pa- tterns used. These patterns were obtained using a well known matrix:

Figure 4. Input and Output patterns for CNN Learning

é 0 0

M = ê- 1 2

ê

êë 0 0

0 ù

Input Output

-1ú

ú

0 úû

In this case we put constraints to select only the matrix B. The parameters obtained are:

First simulation

Figure 5. Input and Output Patterns for CNN Test

é0 0

A = ê0 0

ê

êë0 0

0ù

Input Output

0ú

ú

0úû

é 0 0 0 ù

B = ê-1

ê

1.75

- 0.75ú

ú

êë 0 0

0 úû

I=0

Figure 6. Input and Output patterns for CNN

Learning