La Construcción de la transitividad de la desigualdad con números enteros negativos en la Escuela Secundaria

María Concepción Terríquez Paz Universidad La Salle Guadalajara E-mail:mterriquez@yahoo.com

Asesora: María Guadalupe Moreno Bayardo

Recibido: Abril de 2005. Aceptado: Mayo de 2005

RESUMEN

Esta es una investigación descriptiva y cualitativa en tres etapas, a lo largo de un ciclo escolar, realizada en una escuela secundaria oficial. El objetivo principal fue dar cuenta del proceso mediante el cual los niños y adolescentes construyen la transitividad con números enteros. Se partió de la hipótesis de que hay un paralelismo en la construcción de las operaciones y relaciones de orden, cuando menos en el nivel de las unidades simples. Se utilizaron las entrevistas clínicas para plantear a los sujetos de la muestra situaciones problemáticas y una actividad de correspondencia entre figuras geométricas de diferentes tamaños y etiquetas que hacían referencia a números enteros, positivos y negativos; esto permitió detectar que los niños y adolescentes construyen la transitividad con números enteros en el orden de las unidades simples mediante una secuencia de tres niveles constructivos: alteración, composición e integración. Esta secuencia está correlacionada con el avance de los sujetos en operaciones y ecuaciones aditivas, relaciones de orden, el estatus del cero, la abstracción y generalización y la evolución de los modelos que utilizan para justificar sus respuestas; muestran diferente desempeño de acuerdo con el contexto de la situación problemática, así como un anclaje en lo concreto, esto es, les cuesta trabajo justificar su repuesta a una situación problemática sin hacer referencia a situaciones concretas; además, verbalizan más ante una ecuación que ante una operación directa y muestran un rezago en la toma de conciencia con respecto a lo que pueden hacer con operaciones físicas o mentales.

El objetivo principal de esta investigación fue dar cuenta del proceso mediante el cual los niños y adolescentes construyen la transitividad con números enteros. Los particulares fueron describir las secuencias de desempeño en las que se manifiesta la evolución de los sujetos en su construcción de la transitividad de la desigualdad, dentro de la construcción más general de las relaciones de orden y operaciones con números enteros negativos. Además, construir cuando menos un principio teórico, con carácter hipotético, sobre la construcción de la transitividad de la desigualdad con números enteros, desde una perspectiva psicológica. Se presentan los hallazgos, a manera de una gran hipótesis que tendría que confirmarse con estudios posteriores, además de las limitaciones y los aportes de esta investigación.1

Palabras clave: Construcción de la transitividad, números enteros, resolución de problemas, desigualdad.

ABSTRACT

This is a descriptive and qualitative research in three stages, along a school period, made in an official secondary school The main goal was to realize the process children and adolescents use to built transitivity with whole numbers. A starting hypothesis respect the existence of a paralell link between the development of operations and order relationships, at least at the simple units level. Clinic interviews were applied to provide the subjects of the sample problematic situations and a corresponding activity between geometrical figures of various sizes and labels related to whole numbers, positive and negative; this allowed detecting that chidren and adolescents built transitivity with whole numbers following the simple units order through a sequence of three building levels: alteration, composition and integration. This sequence is correlated with the advance of the subjects with additive operations and equations, order relationships, status of zero, abstraction and generalization, and the models evolution used to justify their answers.

They show a diverse performance acording to the context of the problem, as well as being anchored in the concrete, which means, they find it hard to justify their answers to a problem without refering to concrete situations; besides, they verbalize more in front of an equation than in front of a direct operation and show some falling behing in awareness respect to what they can do with physics and mental operations.

The main objective of the present research was to realize the process through children and adolescents built transitivity with whole numbers. The details were to discover manifested performance sequences where evolution of subjects in the building of uneven transitivity, within a more general construction of order relationships and operations with negative whole numbers. Besides, to built at least a theoretical principle as a hypothesis on unevenness of transitivity construction with whole numbers, from a psychological approach. The findings are shown, as a major hypothesis that needs to be confirmed with later research, considering also the limitations and contributions of this research.

Key words: Transitivity construction, whole numbers, problem solving, unevenness.

1. La escuela secundaria

Los planes y programas de estudio de la Secretaría de Educación Pública (SEP)2 para la educación secundaria enfatizan que la finalidad de la matemática es desarrollar habilidades operatorias y la capacidad para la solución de problemas. La SEP recomienda a los profesores de matemáticas en la escuela secundaria dedicar atención a la enseñanza de los números con signo.

Con respecto a la formación de profesores, en Jalisco hay dos instituciones que por excelencia han sido las formadoras de los docentes en el área de matemáticas para el nivel secundaria: la Escuela Normal Superior de Jalisco y la Normal Superior Nueva Galicia. En las tesis de licenciatura de estas instituciones, uno de los temas frecuentes es la enseñanza de los números negativos, de ahí que hay una aceptación de la importancia que tiene el contenido en la formación de los estudiantes de secundaria.

Además, hay investigadores de prestigio, como Vergnaud,3 quien reconoce que hay serias dificultades en el aprendizaje de los números negativos.

Sin embargo, se considera que la mejor justificación para esta investigación es que los alumnos de secundaria donde se hizo la investigación tienen dificultades para construir los números enteros, positivos y negativos, además de que les cuesta trabajo construir las relaciones de orden con los mismos números. Se presenta como evidencia el caso de una alumna que sí pudo resolver la operación (+8) + (-5) = +3 en un examen escrito, pero que cambia su respuesta ante la contra argumentación:

· Investigadora: ¿Por qué salió un número positivo?

· Alumna: Porque así es.

· I: Tus compañeros dicen que es tres negativo. ¿Tú que crees?

· A: [No contesta, borra la respuesta y escribe –3].4

Algunos(as) alumnos(as) de la secundaria donde se realizó la investigación ordenaban los números negativos de las formas siguientes:

ÿ Por parejas: 0, -1, +1, -2, +2, -3, +3...

Ø Aceptan que los negativos son menores que el cero, pero los ordenan en forma no simétrica: -1, -2, -3..., 0, +1, +2, +3...

Ø Ordenación simétrica: ...-3, -2, -1, 0, +1, +2, +3..., pero diciendo: "Van así porque así dijo el maestro" o "Porque Dios así quiso".5

2. Antecedentes de investigación

Investigaciones anteriores a ésta, como las de Vergnaud6 y Gallardo,7 están centradas en operaciones (suma y resta), no consideran a las relaciones de orden como objeto de estudio y no dan una definición de lo que implica construir el concepto de número negativo.

Gallardo8 realizó su investigación en una escuela secundaria del medio urbano. En el trabajo exploratorio encontró que, además de tener dificultades con las operaciones, los alumnos tienen dificultad para comprender el orden entre enteros. Ella llevó a cabo una propuesta pedagógica con el método chino modificado (la unidad negativa anula a la positiva), e hizo una serie de entrevistas clínicas después del tratamiento, con lo cual identificó 4 diferentes perfiles de desempeño, sin embargo, el orden entre enteros no es un indicador de los mencionados perfiles.

Terríquez9 en una investigación de diagnóstico y propuesta de neutralización en una escuela secundaria femenil, encontró que no se han investigado lo suficiente las relaciones de orden y que hay un paralelismo en la construcción de relaciones de orden y operaciones aditivas, cuando menos en el nivel de las unidades simples.

Cid10 en una investigación documental de corte histórico, sugiere la posibilidad de que los adolescentes tengan obstáculos epistemológicos para la construcción de los números negativos.

Bruno y Espinel11 realizaron su investigación sobre números negativos en la escuela secundaria. Hicieron una comparación entre tres métodos de enseñanza (redactar problemas, resolver problemas y aplicación de reglas), encontrando que los sujetos resolvían con operaciones o con representaciones gráficas de desplazamientos en los tres casos.

Gallardo12 analizó, en otra investigación, la extensión del dominio de los números naturales al dominio de los enteros en la transición de estudiantes de la aritmética al álgebra. Encontró 4 niveles de aceptación del número entero: sustraendo, número relativo, número aislado, número negativo formal. Los primeros 3 niveles fueron observados en 35 estudiantes de secundaria (12-13 años de edad).

La revisión de las investigaciones sobre números negativos muestra que, básicamente, hay dos tipos de propuestas: 1) De neutralización: los números negativos se consideran opuestos a los positivos, por lo que una unidad positiva más una unidad negativa es igual a cero. 2) De desplazamiento: los números negativos se desplazan en sentido contrario que los positivos, ya sea en una recta numérica, un termómetro o el plano cartesiano.13 Pero estas mismas investigaciones no dan evidencia de cuáles son los modelos que los sujetos utilizan cuando resuelven situaciones problemáticas que requieren números enteros. Además, hay un dominio de las operaciones aditivas sobre las relaciones de orden con números negativos, de la cardinalidad sobre la ordinalidad, y una secuencia rígida de enseñanza (primero el orden, después las operaciones aditivas).

A partir de los puntos anteriores, se precisó el objeto de estudio de esta investigación en el contexto de la escuela secundaria: ¿Cuáles secuencias de desempeño muestran los niños y adolescentes en la construcción de la transitividad de la desigualdad con números enteros positivos y negativos? Partiendo de ahí se diseñó un estudio en tres etapas, con sujetos de los tres grados de secundaria, con la intención de inferir el proceso que siguen para pasar de un estado de menor conocimiento de la transitividad con números enteros a otro de mayor conocimiento.

3. Bases teóricas

Las bases teóricas son el constructivismo de Piaget y García,14 con aportes de Delval15 y García,16 entre otros. Piaget17 inició sus investigaciones con el supuesto de que hay una convergencia entre la construcción psicológica del conocimiento, la historia de las ciencias y el análisis formal de las matemáticas. Esto no significa que haya una coincidencia de contenidos entre la psicología, las demostraciones formales y la historia del número negativo, sino que hay una convergencia de los mecanismos de pasaje de un nivel a otro, supuesto del que se comparte en esta investigación.

Se ha constatado que la estructura formal de la transitividad de la igualdad "si X=Y y Y=Z, entonces, X=Z, cualesquiera que sean X, Y y Z", no se adquiere de una vez por todas independientemente de su contenido, sino que se requieren tantas adquisiciones distintas y repetidas como contenidos diferentes a los que pueda aplicarse, por ejemplo, masa, peso, volumen y número natural,18 y en esta investigación se considera que los números enteros son el mismo caso.

Dada una relación asimétrica, tal que a<b, los sujetos comienzan comprendiendo los casos particulares: a<b, b<c, c<d, pero sin hacer conexiones entre ellos. El sujeto comienza a identificar que un elemento e es menor que f, g, h, y mayor que a, b, c y d. Después logrará hacer una intercalación inmediata de elementos sobreañadidos, y podrá invertir la serie tal que a<b, b<c, c<d se transforma en d>c>b>a, entonces se dice que ha construido la transitividad en esa relación.19 La transitividad de la igualdad con números naturales se construye en forma análoga.

En la construcción del número natural, se fusionan las relaciones de clases y las asimétricas, de acuerdo con las investigaciones de Piaget y Szeminska:20 "En consecuencia [...] el número se presenta como la síntesis de la clase y de la relación asimétrica o, lo que viene a ser lo mismo, de la relación simétrica (igualdad) y de las

diferencias (relaciones asimétricas)", y al iniciar esta investigación se esperaba algo semejante con los números enteros.

4. Metodología

De acuerdo con Delval21 y con Hernández Sampieri, Fernández Collado y Baptista Lucio,22 un estudio longitudinal permite observar los procesos de construcción del conocimiento, pero requiere hacer un seguimiento constante de unos cuantos sujetos, lo cual no era posible en esta investigación; con los diseños transversales se pueden tomar muestras de diferentes edades y reconstruir los procesos mediante inferencias, lo que es más fácil para el investigador, pero tiene el inconveniente de que se requieren muestras grandes de sujetos; en cambio, con los diseños mixtos,23 también llamados panel,24 es posible evitar los inconvenientes de ambos tipos de estudio, y reconstruir el proceso con una muestra relativamente pequeña de sujetos de los tres grados de secundaria y entrevistas periódicas, aunque este diseño no ofrece la validez de los estudios longitudinales.

Por estas razones, en esta investigación se utilizó un diseño mixto, consistente en la selección al azar de 21 sujetos de los tres grados de secundaria (seis de primero, siete de segundo y ocho de tercero), para hacer un estudio con entrevistas clínicas en tres momentos del ciclo escolar 2002-2003 (octubre del 2002, y febrero y junio del 2003),25 y describir la construcción de la transitividad de la desigualdad y del número entero mediante inferencias.

Se consideró conveniente entrevistar alumnos(as) de los tres grados escolares ya que se requerían sujetos con desempeños diferentes, que fueran transformándose a lo largo del período en que se realizó la investigación y que permitieran observar el proceso de transición de la transitividad de los números naturales a la transitividad de los números enteros, y estas transformaciones podían esperarse en los estudiantes de la secundaria, ya que el estudio de los números enteros forma parte del curriculum de este nivel educativo. La población de la secundaria donde se hizo este estudio tenía un rango de edad entre los 11 y los 16 años en el turno matutino, pero los sujetos de la muestra tenían entre 12 y 15 años al iniciar el estudio.

Se partió de la hipótesis de que las operaciones suma y resta, y las ecuaciones (es decir, asociatividad, reversibilidad por inversión y transitividad de la igualdad) se construyen paralelamente a las relaciones de orden con enteros (transitividad de la desigualdad y reversibilidad por reciprocidad), cuando menos con las unidades simples, del -9 al +9, y la síntesis de estas operaciones y relaciones da como resultado la construcción del concepto de entero positivo y negativo.

La situación experimental consistió en el planteamiento oral de una serie de 8 problemas sobre números negativos, para observar lo que dicen y hacen los niños y adolescentes de la muestra al resolverlos; en una actividad con material concreto, consistente en hacer una correspondencia uno a uno entre 9 figuras geométricas con la misma forma pero diferente tamaño y 9 tarjetas con las leyendas “tengo 1”, “tengo 2”, “tengo 3”, “tengo 4”, “debo 1”, “debo 2”, “debo 3”, “debo 4” y “no tengo y no debo” y en la entrevista clínica con contra argumentación por parte del experimentador.

En el trabajo de campo se utilizaron tres versiones de un mismo instrumento, con la intención de obtener datos cuyo análisis permitiera describir el proceso de construcción de la transitividad con números enteros, positivos y negativos, y se modificó el instrumento en función de los hallazgos hechos en cada etapa de esta investigación y de las consecuentes transformaciones de las hipótesis de trabajo.

La intención no era ajustar las hipótesis a los datos, sino construir un corpus comprensivo que describiera el proceso de construcción de la transitividad con números enteros positivos y negativos, a partir de los datos, en forma inductiva.

5. Modelo analítico

No se utilizó un modelo de análisis ya elaborado, sino que se construyó uno en forma inductiva, considerando como base el modelo de García,26 quien distingue entre complejo cognoscitivo y sistema cognoscitivo. El complejo cognoscitivo consistió en los datos sin organizar obtenidos con las entrevistas, y el sistema cognoscitivo, en la organización que se hizo de este material para formar un sistema interpretativo sobre cómo los sujetos construyen el número entero en general, y la transitividad en particular.

El análisis pasó por dos niveles interpretativos:

Primer nivel. Análisis e interpretación del material empírico de base, en este caso, de las entrevistas que se aplicaron a los sujetos que participaron en esta investigación.

Segundo nivel. Construcción de principios teóricos, que dieron cuenta del proceso de construcción del número negativo, es decir, se formuló una descripción, con carácter hipotético, sobre la construcción el número entero, en general, y sobre la transitividad, en particular. Esto requirió que a partir del análisis efectuado en el primer nivel, se formulara un principio teórico, coherente con el material empírico de base, pero intentando despegarse de los hechos.

El análisis de datos requirió un modelo flexible que fue modificándose antes, durante y después del trabajo campo. Lo mismo ocurrió con las categorías analíticas. Después de la transcripción de las entrevistas, se separó lo que estaba relacionado con 2 organizadores generales: transitividad de la igualdad y transitividad de la desigualdad. Después, para cada una de las transitividades, se fragmentó la entrevista y se agrupó lo que estaba vinculado con los siguientes organizadores específicos:

I. Relaciones de orden. En este organizador se agrupó lo relacionado con la forma como ordenaban enteros y el estatus del cero en esa relación.

II. Operaciones y ecuaciones aditivas. En este organizador, lo relacionado a sumas, restas, ecuaciones donde la incógnita es un sumando y ecuaciones donde la incógnita es un sustraendo.

III. Modelos. Se consideró a los modelos organizadores como representaciones mentales simples o complejas, que subyacen a una teoría (física, social, numérica, etc.), de acuerdo con Moreno Marimón.27 En el caso de los números

negativos, los modelos que utilizaron los alumnos para justificar una relación de orden fueron: situaciones concretas (como deudas y ganancias), operaciones, desplazamientos (como una recta numérica) y de neutralización (la unidad negativa anula a la positiva).

IV. Abstracción y generalización. Se refiere a enunciados o “formas” que expresaban reglas, procedimientos, justificaciones, operaciones y relaciones, ya sean particulares o generales, con un contenido referido a una situación concreta o sin él.

Los 4 organizadores pertenecen a campos semánticos distintos: los dos primeros (relaciones de orden, operaciones y ecuaciones aditivas) se refieren al contenido matemático que investigué, por lo que son específicos de la transitividad y del número negativo, mientras que los últimos (modelos, abstracción y generalización) se refieren al proceso que siguen los sujetos, y son generales en la construcción del conocimiento.

A partir de este análisis se obtuvo el desempeño de cada uno de los 21 alumnos de la muestra: de cada protocolo se elaboró un reporte que incluye los 4 organizadores específicos, y en cada organizador, fragmentos de las respuestas de los entrevistados y una descripción de lo que el sujeto podía hacer, a partir de categorías que fueron surgiendo durante el análisis de datos y el desempeño del sujeto en cada categoría, (Tabla 1).

En la primera etapa de la investigación, la descripción del desempeño sólo permitía distinguir a los sujetos que podían resolver una situación problemática de aquéllos que no podían, sin embargo, a partir de los hallazgos fue desapareciendo esta dicotomía y aparecieron diversidad de descriptores del desempeño, tales como “resuelve componiendo dos operaciones”, “resuelve con una operación” y “resuelve pero no justifica”.

No fue posible separar completamente el contenido perteneciente a cada uno de los organizadores, ya que un mismo fragmento de la entrevista podía contener elementos que pertenecían a organizadores diferentes, y éstos a su vez, podían pertenecer a campos semánticos distintos (contenido matemático-construcción del conocimiento).

Posteriormente se hizo una tabla de cada uno de los organizadores, incluyendo a los 21 alumnos. Haciendo una lectura horizontal (desempeño h, i, j, k…), se identificó un nivel de desempeño, el cual se agregó en la última columna (Tabla 2).

Tabla 1. Reporte individual.

Tabla 2. Desempeño de la muestra en un organizador.

Después se elaboró una tabla concentrando todos los organizadores específicos y el nivel de desempeño de los sujetos (Tabla 3) y se hizo un retorno reflexivo, esto es, se regresó a los organizadores generales, transitividad de la desigualdad y transitividad de la igualdad, para hacer una descripción de ambas transitividades, a través de los organizadores específicos, categorías, desempeños y niveles de desempeño, haciendo lecturas horizontales de un mismo sujeto y lecturas verticales entre sujetos.

Uno de los hallazgos de la primera etapa del trabajo de campo fue que los sujetos verbalizaban más cuando resolvían ecuaciones, lo que llevó a la hipótesis de que los sujetos resolvían tan rápidamente las operaciones directas que no se daban cuenta de cómo lo hacían; en cambio, las ecuaciones, por ser procesos inversos, implican mayor grado de dificultad, lo que les hacía tomar conciencia del proceso, y en la segunda etapa del trabajo de campo se incluyeron más reactivos de ecuaciones que de operaciones.

Asimismo, varios de los sujetos cambiaron la ordenación de los enteros durante la entrevista, por lo que en la segunda etapa se incluyeron actividades de ordenación en dos contextos diferentes, para observar qué tan sólida era su respuesta. Estos cambios en las hipótesis de trabajo, llevaron consigo cambios en las categorías analíticas y en los formatos de las tablas.

Se elaboraron tablas comparativas para cada uno de los organizadores, con los resultados de la primera y la segunda etapa (Tabla 4), registrando los cambios observados, y revisando las tablas de desempeño una y otra vez (Tabla 2), para hacer nuevas conjeturas y nuevas hipótesis.

Después del análisis de la segunda etapa de entrevistas se observó que los sujetos tenían retrocesos aparentes. Así, un sujeto que había tenido un nivel de desempeño 2 en la primera etapa, mostró un nivel 1 en la segunda; sin embargo, junto con las variaciones de nivel, también había variaciones en el contexto del problema, por lo que se consideró otra hipótesis de trabajo: los desempeños y los niveles de desempeño varían con el contexto. Esto llevó consigo modificaciones en las categorías analíticas y en los formatos de las tablas, en las que se hicieron especificaciones del contexto de la

situación problemática o actividad de correspondencia planteada a los alumnos (Tablas 5, 6 y 7).

Tabla 3. Niveles de desempeño de la muestra.

Tabla 4. Cambios en el desempeño de la muestra en un organizador.

Por último, como se elaboraron las tablas a partir de hipótesis y categorías distintas, no fue posible (ni pertinente) hacer una comparación entre las 3 etapas de manera directa, por lo que se hizo una comparación de elementos análogos, esto es, elementos de las tablas que podían ser comparables entre sí porque eran observaciones hechas a un mismo sujeto, y compartían el mismo contexto de situación problemática planteada a los alumnos y el mismo tipo de relación o de operación; por ejemplo, ecuaciones donde la incógnita es un sumando en el contexto de deudas y ganancias, en la segunda y la tercera etapa. O bien, situaciones problemáticas con el mismo tipo de relación o de operación, y en la misma etapa, pero en diferente contexto.

El análisis de datos permitió identificar tres niveles de desempeño en la construcción de la transitividad de la desigualdad: alteración, composición e integración, y niveles análogos para la transitividad de la igualdad. No se seleccionaron sujetos ‘iniciales’, ‘intermedios’ y ‘avanzados’, sino que fueron elegidos al azar, y después se les dio forma y sentido a los hallazgos.

¿Por qué tres exactamente? Se consideró que el objeto de estudio de esta investigación, la construcción de la transitividad con enteros negativos, implicaba cambios a lo largo del tiempo, y estos cambios se observaron en un momento incipiente de la construcción, o estado inicial; un momento de logro de la construcción, o estado final, y un momento de transición del estado inicial al estado final. Con base en lo detectado, se puede afirmar que siempre es posible describir cuando menos tres niveles de la transformación de un proceso cualquiera.

De acuerdo con la postura teórica que sustenta esta investigación, los tres niveles podrían estar vinculados con estadios, es decir, que fuera obligado el paso por cada uno de los niveles para la construcción de la transitividad, sin embargo, los alcances y límites de esta investigación no permiten afirmarlo; pero sí queda como una hipótesis de trabajo para posteriores investigaciones.

Tabla 5. Ficha individual.

Tabla 6. Desempeño de la muestra en un organizador en diferentes contextos.

Tabla 7. Nivel de desempeño de la muestra en diferentes contextos.

Los tres niveles de construcción de la transitividad se corresponden con los tres niveles propuestos por Piaget y García28 para describir funcionalmente la construcción del conocimiento: 1) Nivel intraobjetal, durante el cual los sujetos analizan las características del objeto del conocimiento, pero sin establecer relaciones entre ellas. 2) Nivel interobjetal, durante el cual el sujeto reconoce las relaciones y las transformaciones. 3) Y por último, nivel transobjetal, caracterizado por la constitución de la estructura de conjunto.

1. Confiabilidad y validez

Las siguientes características le confieren confiabilidad y validez al instrumento empleado en esta investigación:

Delval,29 considera la posibilidad de hacer cambios en las entrevistas, pero sugiere no introducir demasiados cambios debido a que esto dificulta la comparación entre sujetos. En esta investigación se modificó el instrumento en las tres etapas de la investigación, sin embargo, sólo se compararon elementos análogos que sí podían ser comparados, por lo que las transformaciones observadas en los sujetos no se deben a los cambios realizados en el instrumento.

Los sujetos que participaron en esta investigación tuvieron diferentes desempeños en la actividad de correspondencia entre las figuras geométricas y las tarjetas, lo que es un indicador de que la actividad tiene un grado de complejidad que permite percibir o discriminar el desempeño de los sujetos, lo que además le da validez al instrumento. Análogamente, los sujetos presentaron diferentes desempeños en la resolución de las situaciones problemáticas y actividades de correspondencia planteadas.

Para dar cuenta de la transformación a lo largo del tiempo, se puede utilizar un diseño transversal con sujetos de diferentes edades, reconstruyendo el proceso con el supuesto de que los sujetos construyen la transitividad con enteros negativos a través de niveles consecutivos, lo que reduce el trabajo de campo a una etapa única; sin embargo, con un diseño mixto se ha podido reconstruir el proceso sin tener que recurrir a dicho supuesto.

Un indicador de que las diferencias de desempeño se debían al avance en la construcción del número entero es que había sujetos que, aunque estaban en algún nivel como “integración de la transitividad de la igualdad”, tenían rasgos del nivel anterior, esto es, las creencias no desaparecían abruptamente, y se dieron varios casos de alumnos que mostraban rasgos de dos niveles contiguos; como una alumna, quien en la exploración 2 resolvió una situación problemática de dos formas: componiendo con dos operaciones y con una sola operación (integración).

Los alumnos progresaban en cada etapa, lo que era de esperarse dado que eran sujetos escolarizados y el contenido matemático que se investigó forma parte del curriculum de la escuela secundaria, y esto da muestras de que el instrumento permite indagar si han ocurrido procesos de transformación. Además, de acuerdo con la postura teórica y el objetivo de esta investigación, era fundamental dar cuenta de cómo los sujetos pasaban de un estado de conocimiento a otro estado más avanzado, y se presentan los hallazgos correspondientes. Además, se presenta una descripción del trabajo analítico, lo que permite que los lectores puedan reconstruir el procedimiento utilizado en esta investigación.

Lo fundamental es que el instrumento “mida lo que pretende medir”, sin que esto implique datos cuantitativos, sino que sea un instrumento que permita dar cuenta del fragmento de la realidad que se pretende conocer. Una crítica que podría hacerse es con respecto a lo abierto de algunas situaciones problemáticas, lo que permitía que algunos sujetos dieran respuestas iniciales como “Así califica el maestro de Historia”, “Portándome bien”, “Hay cambios en el clima”, sin embargo, era suficiente hacerles otra pregunta para que expresaran enunciados que reflejaban su construcción del número entero, tales como “¿Cómo?”, “¿Por qué?” y, la que ayuda a que los sujetos continúen hablando sin sugerirles una respuesta, “¿Y?”. La mayoría de las preguntas podían ser contestadas con múltiples respuestas, lo que es necesario en una entrevista clínica, esto es, hay que hacer preguntas que ubiquen a los sujetos en una parcela de la realidad, pero que no los obliguen a dar determinada respuesta.

De acuerdo a la postura epistemológica y teórica de esta investigación, la confiabilidad de un sistema cognoscitivo no depende de cada afirmación, sino de la consistencia del sistema que se ha construido. Y lo más importante: el objetivo de esta investigación no era demostrar o generalizar, sino describir cómo los niños y adolescentes construyen la transitividad con números enteros en el contexto de la escuela secundaria, dentro de los límites y alcances que impone el tipo de estudio y el tamaño de la muestra.

2. Hallazgos

Los diversos desempeños y avances en las tres etapas de la investigación que presentaron los sujetos sugieren una secuencia constructiva de las operaciones aditivas, sin ser lineal: A) Suma de números enteros, y restas sólo en el caso particular de 2 enteros, (-a)-(-b), tal que a>b.30 B) Ecuaciones donde la incógnita es un sumando y

restas con el sustraendo mayor que el minuendo, (+a)-(+b), tal que a<b, y C) Restas con doble inversión del número, (+a)-(-b)=+c, y ecuaciones donde la incógnita es un sustraendo.31

Además, la forma como pasan de no resolver a resolver ecuaciones es mediante el procedimiento de componer la respuesta con dos operaciones, primero sin considerar al cero como punto de referencia, después considerándolo.

De acuerdo con las transformaciones mostradas por los sujetos de la muestra, la ordenación de enteros pasa por 3 momentos. Primero ordenan por parejas, ya sea +1, - 1, +2, -2… ó -1, +1, -2, +2…; posteriormente separando enteros +1, +2, +3, -1, -2, -3 ó

-1, -2, -3…, +1, +2, +3, y por último, ordenan simétricamente: …-3, -2, -1, +1, +2, +3… La evidencia a favor es que los alumnos que presentaron cambios en la ordenación de enteros lo hicieron en esta secuencia constructiva.

Se reconsideró el término paralelismo, que inicialmente se había definido como “avance correlacionado y simultáneo”, y se redefinió como “avance correlacionado pero no simultáneo”, debido a los desfases observados en la construcción de las operaciones aditivas y las relaciones de orden. Sin embargo, la correlación se manifestó en lo siguiente:

a. Hay una construcción progresiva de las relaciones de orden y operaciones y ecuaciones aditivas con enteros, es decir, no hay una secuencia primero relaciones de orden, después operaciones y ecuaciones.

b. Los sujetos justifican las relaciones de orden con operaciones aditivas.

c. El cero relativo juega un rol importante en la resolución de ecuaciones, en particular donde la incógnita es un sustraendo.

d. Hay desfases en la construcción de las operaciones aditivas, las relaciones de orden y el estatus del cero, pero en su más alto nivel de desempeño tienden a converger en los sujetos que muestran mayor avance en todos los contextos de las situaciones problemáticas.

Dado que la transitividad de la igualdad y la desigualdad son elementos del número entero, se esperaba encontrar otro paralelismo constructivo de ambas transitividades.

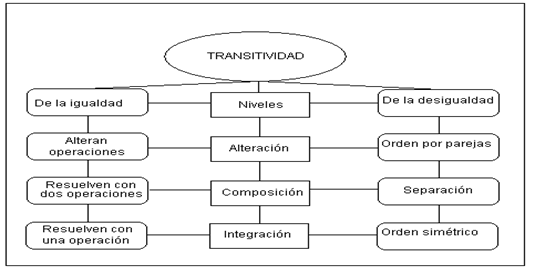
Los hallazgos permiten afirmar, a manera de hipótesis, que sí hay un paralelismo análogo al de las operaciones y relaciones de orden, y que se trata de procesos no simultáneos. Esta afirmación equivale a decir que no hay una secuencia “primero transitividad de la desigualdad, después transitividad de la igualdad”, sino que ambas transitividades se van construyendo gradualmente, y que la culminación de ambas (integración del orden, en el caso de la desigualdad; integración en una operación, en el caso de la igualdad) no se da al mismo tiempo, puede ser que primero logren una de las dos transitividades. Además, se identificaron tres niveles constructivos para la transitividad de la desigualdad y la igualdad (Figura 1):

Un primer nivel llamado “alteración”, consistente en que los sujetos incorporan los enteros negativos, pero los someten a las mismas reglas que a los números naturales. Con el término alteración se hace referencia al hecho de que los sujetos alteran el signo de los números o del operador, pero no ambos, y aplican la transitividad aún en el dominio de los números naturales, por ejemplo: “(+5)+(-2)=(+5)+(+2) y (+5)+(+2)=(+7) entonces (+5)+(-2)=+7”. Ordenan por parejas de enteros (+1, -1, +2, -2… ó -1, +1, -2, +2…), reconociendo un valor diferente para los enteros negativos, pero en forma cualitativa y particular, a cada número lo consideran menor (o mayor) que su simétrico.

Un segundo nivel llamado “composición”, que es cuando los sujetos además de incorporar los enteros negativos, comienzan a operar con ellos reconociéndolos como diferentes a los números positivos, pero necesitan componer sus soluciones con dos operaciones, en particular, cuando resuelven ecuaciones o procesos inversos, por ejemplo, la ecuación (-4)+( )=+5, la resuelven sin considerar al cero como punto de referencia: “(+5)+(-4)=+1, (+1)+(+4)=(+5) entonces (-4)+(+5)+(+4)=+5 y (+5)+(+4)=+9”, o

bien, considerando al cero como punto de referencia “(-4)+(+4)=0 y 0+(+5)=+5 entonces (-4)+(+4)+(+5)=+5 y (+4)+(+5)=+9”. Ordenan separando enteros (-1, -2, -3, +1, +2, +3… ó +1, +2, +3, -1, -2, -3…), y el valor diferente para los enteros negativos se ha generalizado, todos los enteros negativos son menores (o mayores) que los positivos, pero aún no se ha cuantificado esta relación.

Un tercer nivel llamado “integración”, que se caracteriza porque los sujetos logran resolver ecuaciones con una sola operación y aplican la transitividad en el dominio de los enteros positivos y negativos. Ordenan en forma simétrica (-3, -2, -1, 0, +1, +2, +3…), y se ha cuantificado el valor diferente de los negativos, además de haberse generalizado (todos los negativos son menores que los positivos), por lo que aceptan que -3 es el inverso aditivo o simétrico de +3, esto implica que aceptan que -3 es menor que +3, que todos los negativos son menores que +3 y que -3 y +3 tienen el mismo número de unidades, pero con diferente valor relativo. Es cuando los sujetos aceptan que si A=B y B=C entonces A=C, y que si A<B y B<C entonces A<C en el caso de que A, B y C sean números enteros, positivos y negativos.

Figura1.Niveles de construcción de la transitividad.

El estatus del cero como absoluto, como el mayor de los números o como relativo, también juega un rol importante en la construcción de la transitividad. Se esperaba una relación entre los progresos de la transitividad y el estatus del cero, sin embargo, no fue así. Pueden darse casos como los siguientes: que un alumno ordene separando enteros, pero siga considerando un cero absoluto: 0…-1, -2, -3…, +1, +2, +3…, o bien, que lo considere el mayor de los números: …-1, -2, -3…, +1, +2, +3…, 0. Sin embargo, se observó en los sujetos más avanzados una tendencia a ordenar en forma simétrica con cero relativo: -3, -2, -1, 0, +1, +2, +3…

A partir de los hallazgos de la investigación, se descubrió lo siguiente: cuando un alumno ordena por parejas –1, +1, -2, +2, -3, +3....0, y coloca al cero en el lugar del mayor, es matemáticamente incorrecto, pero es un avance con respecto a ordenar 0, -1,
+1, -2, +2..., ya que implica una movilidad de pensamiento. La movilidad se debe a que pueden sumar enteros positivos y negativos, cuando menos en contextos específicos; el orden está construido con la suma de simétricos: (-1) + (+1) = 0, (-2) + (+2) = 0, (-3) + (+3) = 0... Los sujetos colocan el cero al final, de menor a mayor, porque es el resultado de las sumas anteriores.

Se obtuvieron hallazgos que contradicen parcialmente lo expuesto por Beth y Piaget32 con respecto al avance simultáneo de la seriación, la clasificación y la conservación del número natural. En esta investigación, se observó que los desfases son la norma y los avances en fase de todos los elementos o aspectos del número entero son la excepción, es decir, un mismo sujeto, en situaciones problemáticas en el mismo contexto, puede presentar mayor avance en relaciones de orden que en operaciones, o al contrario.

En el caso de que la exigencia de la necesidad y la confianza en las reglas fueran necesarias para la construcción del número entero, permitirían que los sujetos acepten soluciones con enteros positivos y negativos que no están dadas por sus experiencias, sin embargo, lo que se encontró es que los sujetos resuelven las situaciones problemáticas más cercanas a su entorno y experiencias (calificaciones, deudas y ganancias). A partir de los hallazgos se puede afirmar que un primer nivel de equilibrio en la construcción del número entero se da cuando los sujetos pueden resolver situaciones problemáticas que requieren para su solución relaciones de orden con cero relativo y operaciones y ecuaciones aditivas, en diversidad de contextos y con unidades del -9 al +9; dentro de este proceso los sujetos pasan por una secuencia de desempeño en la que se manifiesta la construcción de la transitividad de la igualdad y la desigualdad: alteración, composición e integración. A este primer nivel de equilibrio se le llamó “concepto de número entero”. Otros elementos que intervienen en este proceso evolutivo son (Figura 2):

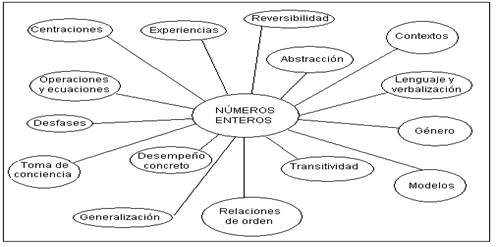
Figura2.Elementosque intervienen en la construcción del número entero. Dimensión cognitiva.

• El lenguaje y la verbalización. Los sujetos verbalizan más ante un problema que exige un proceso inverso que ante uno directo, esto es, no suelen dar explicaciones sobre cómo resuelven una suma, y verbalizan más cuando resuelven ecuaciones.

• Las experiencias del sujeto en cada contexto de la situación problemática que tiene que resolver. En el caso de los sujetos que participaron en esta investigación, los contextos que les resultan más accesibles son “calificaciones” y “deudas y ganancias”, y los menos accesibles, “tiempo” y “temperaturas”, y los sujetos que se encuentran en el tercer nivel de construcción del número entero ya han generalizado los contextos.  De acuerdo con varias investigaciones33 este diferente desempeño en cada contexto se da en  los  sujetos  de  todos  los  niveles  educativos  y  en  todos  los  contenidos  de  las
  matemáticas, y no se debe a dificultades cognitivas sino a la especialización del conocimiento debido a la experiencia.

33  a) Castro, E., Rico, L., Castro E., Estructuras aritméticas elementales y su modelización, Bogotá: Grupo Editorial Iberoamérica, 1995.

• Saiz, I., “Dividir con dificultad o la dificultad de dividir.”, en C. Parra e I. Saiz (Comp.), Didáctica de las matemáticas, aportes y reflexiones, pp. 185-217, Argentina: Paidós Educador, 1994.
• Hoyos, V., “Un estudio exploratorio sobre la asignación de sentido a las representaciones básicas de la variación, al término de la primaria y el inicio de la secundaria”, en Educación Matemática, Vol. 6, Nº 3, pp. 65- 81, México: Grupo Editorial Iberoamérica, 1994.
• Ojeda, A. M., “Contextos, representaciones y la idea de probabilidad condicional”, en F. Hitt Espinoza (Edit.), Investigaciones en matemática educativa, (pp. 291-310). México: Grupo Editorial Iberoamérica, 1996.
• Sánchez, E., Hernández, R., “Análisis de resultados de un cuestionario sobre la regla del producto en probabilidad, aplicado a estudiantes de bachillerato y primer año profesional”, en Memorias del VII Simposio Internacional en Educación Matemática Elfriede Wenzelburger, UPN (pp. 152-158). Cd. de México: Grupo Editorial Iberoamérica, 1999.
• Waldegg, G., De Agüero, M., “Habilidades cognoscitivas y esquemas de razonamiento en estudiantes universitarios”, en Revista Mexicana de Investigación Educativa, Vol. 4, Nº 8, pp. 203-244, 1999.
• Valiente, S., “Análisis de 4 algoritmos operatorios en investigación de campo con adultos analfabetas”, en

EducaciónMatemática, Vol. 7, Nº 2, pp. 60-73. México: Grupo Editorial Iberoamérica, 1995.

• Bruno, A. y Espinel, M. C., op. cit.
• Gallardo, A., op. cit., “El paradigma…