Métricas de complejidad para la transformación del problema de la detección de cáncer basado en mamografías1

RESUMEN

Desde el GRSI (por sus siglas en inglés), Grupo de Investigación en Sistemas Inteligentes de la Salle, se trabaja en diferentes vertientes del problema de la detección de cáncer de mama. Las líneas de investigación han abordado el procesado de la imagen de las mamografías, la extracción de datos para configurar la descripción de los atributos relevantes y la predicción del diagnóstico médico con clasificadores aplicando técnicas de aprendizaje automático.

El problema parte de una base de datos en la cual se describen las microcalcificaciones presentes en una mamografía. Cada paciente dispone de un conjunto variable de microcalcificaciones que para ser tratadas deben resumirse en un caso sintético. Clásicamente, este aspecto se ha resuelto realizando la media de las descripciones de todas las microcalcificaciones y de este modo obtener un único caso. Sin embargo, este procedimiento, conocido como aplanamiento de los datos, no está respaldado por ningún fundamento. Por lo tanto, este proyecto pretende evaluar posibles transformaciones y determinar cuál es la mejor para sintetizar un caso.

En una primera fase, se presenta el estudio de diferentes métodos para transformar las microcalcificaciones y, en una segunda fase, el análisis que indica cuál es la transformación que aporta más información para la clasificación. Para ello, se aplican varias métricas de complejidad que caracterizan la dificultad del problema basándose en el conjunto de datos propuesto. Para completar el proyecto y extraer las conclusiones sobre las propuestas de transformación y la garantía que ofrecen las métricas, los resultados obtenidos se validan con los resultados generados por sistemas clasificadores.

Palabras clave: microcalcificaciones, mamografías, clasificadores, métricas de complejidad.

ABSTRACT

In Intelligent Systems Research Group, at La Salle University (GRSI, for its initials in English) a work on the mammal cancer detection problem is developed from several approaches of the problem. The research lines have addressed the mammography images, processing the data extraction to configure the relevant attributes description, and the medical diagnose prediction with classifiers, applying techniques of automate learning.

The starting point of the problem is a data base where present micro- calcifications in a mammography are described. Each patient has at her disposal a variable set of micro-calcifications that, in order to be treated must be summarized in a synthetic case. Classically, this aspect has been solved proceeding to measure the descriptions of all micro- qualifications to obtain, under these terms, a unique case. Nevertheless, this procedure, known as data flattening, is not supported by any foundation. Thus, this project aims to evaluate possible transformations and determine which is best to synthesize a case.

In a first phase, the study of different methods to transform micro- calcifications is presented; and, in a second phase, the analysis indicating, which is the transformation that provides more information for classification. In order to do so, several complexity metrics characterizing the problem’s difficulty based on the proposed set of data are presented. To complete the project and extract conclusions on the transformation proposals and the guarantee offered by metrics, the achieved results are validated against results generated by classifying systems.

Key Words: micro-calcifications, mammography, classifiers, complexity metrics

1 PLANTEAMIENTO DEL PROBLEMA

El cáncer de mama es el cáncer de mayor incidencia entre las mujeres y, aunque en general se atribuye al género femenino, también se declara en un 1% de los hombres.

El índice de superación de esta enfermedad depende de la fase en que se encuentra el tumor en el momento de su detección; por este motivo, médicos y especialistas recomiendan revisiones y exámenes radiológicos periódicos, siendo la mamografía una de las pruebas más solicitadas en el diagnóstico precoz. Se trata de una radiografía de la mama, donde pueden localizarse posibles lesiones en el tejido mamario. Lo que revela la posibilidad de cáncer son las calcificaciones casi microscópicas de los vasos de la mama, conocidas como microcalcificaciones, que pueden corresponder a tumores malignos o benignos, o pertenecer simplemente a un proceso natural. El principal problema es que no existe un único indicio para determinar la presencia de este cáncer y se desconocen sus causas, aunque se hayan catalogado una serie de factores de riesgo que pueden predisponer a sufrirlo.

Algunos de ellos son antecedentes familiares por línea materna, inicio precoz de la menstruación, menopausia tardía, gestación después de los 30 años, no haber tenido hijos y haber estado expuesta a radiaciones ionizantes. No obstante, el 80% de los casos no presentan ninguno de estos cuadros. Entonces a partir de varios estudios se han destacado cuáles son los atributos relevantes de las microcalcificaciones, como el tamaño y la distribución. Sin embargo, no han sido suficientes para que la medicina haya podido elaborar una sintomatología que permita establecer un diagnóstico fiable sin la necesidad de acudir a pruebas invasivas como la biopsia quirúrgica.

Para reducir la aplicación de estas técnicas, la investigación científica ha propuesto el aprendizaje automático, con métodos de aprendizaje supervisado donde el material de base son los históricos de pacientes. El procedimiento consiste en digitalizar la mamografía y, mediante técnicas de procesado de la imagen, extraer el valor de los atributos que previamente oncólogos y radiólogos han considerado características relevantes de las microcalcificaciones para la construcción del conjunto de datos. Todos los casos que participan en la extracción de atributos disponen del diagnóstico real obtenido mediante biopsia. Para diagnosticar a una nueva paciente, se utiliza un sistema clasificador, que determina el resultado a partir de la base de datos, que maneja dos tipos de clase: benigno y maligno. Por lo tanto, la extracción y el análisis de las microcalcificaciones requieren cuatro fases: digitalizar las mamografías, detectar las áreas sospechosas, extraer los valores de los atributos de las microcalcificaciones de la mamografía digitalizada y analizar los atributos aplicando técnicas de aprendizaje automático como clasificadores. El éxito de estos últimos depende de la complejidad de la base de datos; una condición necesaria es resumir los datos de cada paciente en un único caso, de aquí el uso de las métricas de complejidad. En este proyecto2 se quiere comprobar la posible relación lineal entre la complejidad de una base de datos y el error cometido por el clasificador.

2 JUSTIFICACIÓN

El problema de la detección de cáncer de mama es un problema de clasificación en el cual hay que predecir, a partir de un conjunto de microcalcificaciones, si el paciente puede desarrollar o no la enfermedad. Las microcalcificaciones agrupadas en mamografías pueden constituir lesiones malignas y por consiguiente se consideran como la anticipación de un proceso canceroso. La caracterización de las lesiones supone un problema complejo independientemente de la experiencia del radiólogo y esto queda demostrado por la gran cantidad de biopsias que se realizan, todas ellas para solventar situaciones dudosas. La asistencia por computadora aparece como una solución que proporciona soporte al diagnóstico del especialista y disminuye tanto falsos positivos como negativos.

2.1 Proceso de diagnosis precoz

El análisis de las mamografías engloba diferentes áreas de investigación como el tratamiento y procesado de la imagen, la manipulación de conjuntos de datos y las técnicas de aprendizaje automático. La figura 1 presenta las fases del proceso de diagnosis precoz.

Figura 1. Proceso de diagnosis precoz.

Se diferencian cuatro etapas: la recopilación de datos, la transformación del conjunto de datos, el entrenamiento del sistema clasificador y la predicción de un nuevo caso. En primer lugar, se efectúa el tratamiento de la imagen de todas las mamografías de cada paciente para obtener una base de datos donde se almacena el conocimiento. El siguiente paso consiste en transformar el conjunto de casos resultante para aplanar los datos y que éstos puedan ser tratados por el sistema clasificador. Con este proceso se intenta simplificar la estructura geométrica del conjunto sin perder información. La calidad de la transformación se determina utilizando las métricas de complejidad y se verifica con el porcentaje de aciertos del sistema clasificador, entrenado con el conjunto de datos transformado. Finalmente, el diagnóstico de un nuevo caso se realiza con el motor de clasificación generado en la fase de entrenamiento. Cada nueva entrada ha de ser sometida al tratamiento de la imagen para extraer la descripción del caso. El detalle de las diferentes etapas del proceso se referencia al estudio realizado por el GRSI en [1].

Extracción de atributos

La forma y la distribución son características de las microcalcificaciones que ayudan a elaborar el diagnóstico sobre la probabilidad de cáncer y se definen a partir de un conjunto de 21 atributos (tabla 1).

Tabla 1. Atributos descriptores de una microcalcificación.

ATRIBUTO Descripción

Etiqueta Identificador numérico de la microcalcificación.

Área Número de píxeles que forman la μCa3.

Perímetro Longitud total de los límites de la μCa.

Compacidad Esfericidad, derivada del perímetro (P) y del área (A) de la

μCa, se calcula como P²/4πA.

Caja mínima X,Y Coordenadas del extremo inferior izquierdo de la μCa.

Caja máxima X,Y Coordenadas del extremo superior derecho de la μCa.

3 Microcalcificación.

Existe una gran diversidad de microcalcificaciones y posibles clasificaciones. Una de ellas las separa en dos categorías, según la distribución en grupo y según la morfología individual. [2] Las microcalcificaciones pueden ser benignas o sospechosas de malignidad según el tamaño, el aspecto, y la distribución. Las malignas acostumbran a destacar por ser numerosas, agrupadas y pequeñas, con forma de punto o alongadas, pero su tamaño, forma y densidad puede variar. Contrariamente, las microcalcificaciones benignas, más homogéneas en tamaño y forma, con una distribución más difusa, se distinguen por ser grandes, redondas y menos numerosas que las malignas. Sin embargo, su caracterización es un problema complejo ya que en muchos casos la estructura de las microcalcificaciones malignas no difiere de las benignas (véase figura 2).

Figura 2. Ejemplos de microcalcificaciones.

Base de datos del conjunto original

El conjunto de datos suministrado en la fase de requerimientos ha sido cedido por el Hospital Universitario de Girona, Doctor Josep Trueta. Está compuesto por 216 instancias donde destacan 121 casos benignos y 95 malignos diagnosticados por biopsia quirúrgica. Las características de las microcalcificaciones se describen mediante 21 atributos comentados en la tabla 1 (fig. 3).

Figura 3.Estructuración de los datos.

2.2 Complejidad de la clasificación

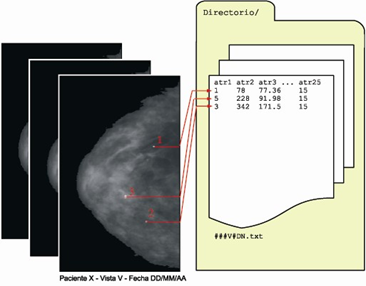
El error promedio cometido por el clasificador y/o el porcentaje de aciertos son los estimadores hasta ahora utilizados para determinar la corrección del sistema. Cuando se aplica un clasificador en un determinado problema y se mide su porcentaje de aciertos (o errores), esta medida depende de dos factores:

• La complejidad del problema.

• La calidad del clasificador propiamente.

Típicamente se ha centrado la atención en la construcción de clasificadores intentando que éstos sean cada vez más precisos y rápidos, olvidando el estudio de la complejidad inherente al problema que a menudo es la causa del error del clasificador.

La dificultad de un problema está sujeta a tres causas [3,4]:

• Ambigüedad de las clases: Algunos problemas de clasificación contienen clases que no se pueden distinguir dado que hay instancias que, para clases opuestas, presentan los mismos valores en todos los atributos. Este fenómeno es debido a la ambigüedad intrínseca de la clase o a la falta de atributos discriminantes. Para este último caso, se puede redefinir o ampliar el conjunto de atributos. La ambigüedad de las clases fija un límite inferior de la tasa de error, llamado error de Bayes. Estas propiedades se cumplen independientemente del tamaño o la dimensión del espacio de atributos (ver fig. 4).

Figura 4. Clases ambiguas a causa de (a) la definición de la clase; (b) la falta de atributos.

• Complejidad de la frontera: Otros problemas pueden tener una frontera de separación entre clases muy compleja que requiere un conjunto de descripción más amplio o un algoritmo complejo para representarla. La complejidad de la frontera se puede caracterizar con la complejidad de Kolmogorov o la longitud mínima del programa que se necesita para reproducirla. Esto es independiente de la ambigüedad de las clases y del tamaño del conjunto de entrenamiento, ya que disponiendo de suficientes puntos sin ambigüedad en la clase, la descripción de la frontera puede ser todavía compleja. En el peor de los casos se puede necesitar una enumeración de todos los puntos con la clase relativa (fig. 5).

Figura 5. Problemas de clasificación de diferente complejidad geométrica: (a) problema linealmente separable con márgenes anchos y clases compactas; (b) problema linealmente separable con márgenes estrechos y clases dispersas; (c) problema con frontera de clases no lineal; (d) clases entrelazadas con una distribución de tablero de ajedrez.

• Conjunto de ejemplos reducido y dimensión del espacio de atributos: La cantidad y representatividad de las instancias del conjunto de entrenamiento influye en la capacidad de generalización del clasificador. Con un conjunto de entrenamiento pequeño se puede errar en la estimación de la complejidad del problema y catalogarlo de simple; es probable que los datos no sean suficientemente representativos y no reflejen la totalidad del problema. Si el número de ejemplos de entrenamiento es insuficiente y la dimensionalidad en número de atributos es elevada, pueden provocar que, aunque se obtenga un buen resultado de clasificación en entrenamiento, los aciertos en la fase de test con nuevas instancias sea pobre e inestable.

Las imperfecciones en la precisión de los clasificadores son una consecuencia de la combinación de estos aspectos, lo que indica que la mejora no está tanto en la construcción del clasificador sino en el análisis de la complejidad del conjunto de datos. En definitiva, nace un nuevo ámbito de estudio que centra su atención en los datos y no sólo en la calidad del clasificador. Las métricas muestran la geometría del conjunto de datos y destacan su complejidad para poder determinar su naturaleza, como por ejemplo si el problema es linealmente separable.

Empíricamente se ha observado que los resultados de los sistemas clasificadores dependen de las características del conjunto de datos [5]. El desconocimiento de esta dependencia ha comportado que en los estudios, tanto teóricos como prácticos realizados hasta la fecha, se hayan obtenido resultados poco determinantes e insatisfactorios en los límites de las clases. De hecho, las métricas actuales se basan en aspectos estadísticos y descripciones teóricas de la información cuando en realidad deberían evaluar la geometría de los datos. El objetivo de las métricas de complejidad consiste en destacar las características geométricas de la distribución de las clases y proporcionar un indicador que estime cómo están separadas o entrelazadas, es un factor que puede resultar crítico en la precisión de la clasificación. A partir del estudio del conjunto de datos, se puede predecir el comportamiento de varios clasificadores que se basan en el mismo modelo geométrico. Una medida clásica de la dificultad del problema es el error medio cometido por el clasificador elegido. Pero las métricas van más allá de esta elección. Tin Kam Ho, en sus estudios, [6,7] intenta representar los problemas del mundo real como puntos en un espacio, de tal manera que las agrupaciones de los puntos creen dominios de resolución de un determinado clasificador y permitan identificar un catálogo de problemas con una complejidad equivalente. Tanto en el aprendizaje supervisado como no supervisado, las estructuras agrupadas son características esenciales en los problemas de discriminación. La figura 6 ofrece una perspectiva en sólo dos dimensiones para poder ilustrar la idea de dominio de competencia de los clasificadores, pero conceptualmente el espacio podría construirse sobre n dimensiones correspondientes a diferentes métricas de complejidad calculadas.

Figura 6.Representación espacial de la complejidad de problemas reales.

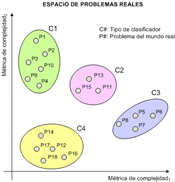
En este esquema confluyen dos conceptos, la complejidad asociada a un problema y el nivel de complejidad que admite un clasificador para conseguir el máximo rendimiento. En el espacio de la complejidad de los problemas se muestran las diferentes zonas de influencia de cada clasificador. De esta manera, cada vez que se trata un nuevo problema, éste se sitúa en el espacio y se conoce el clasificador que mejor se adapta a su geometría y que permite obtener mejores resultados de clasificación. Por ejemplo, idealmente los problemas P11, P13 y P15 según las métricas de complejidad MC1 y MC2 se encuentran en el dominio del clasificador C2.

El estudio de los datos para determinar la complejidad de un problema es una disciplina reciente. Las métricas de complejidad se reparten en tres grandes familias que se centran en diferentes aspectos de los datos: el nivel de discriminación de los atributos individualmente, la separabilidad de las clases y la topología de las clases como su grado de solapamiento y su distribución en hiperesferas. La literatura recopila estas métricas pero se intuye la dificultad de su comprensión puesto que es difícil representar gráficamente qué significa cada medida. La extracción de información de los datos no permite establecer exactamente la relación entre la geometría real y la medida numérica. Ciertamente, algunas métricas se muestran más estables que otras y son éstas las que intervendrán en la fase de experimentación.

3 OBJETIVOS

Los objetivos del proyecto se concentran en tres bloques:

1. Realizar el estudio y la implementación de diferentes métodos para transformar el conjunto de datos extraídos de las mamografías de cada paciente.

2. Estudiar las diferentes métricas de complejidad que recoge la literatura e implementar las más destacadas para aplicarlas a los conjuntos de transformación generados.

3. Validar los resultados de las métricas de complejidad con el test de los conjuntos transformados mediante sistemas clasificadores.

4 METODOLOGÍA

El alcance del proyecto queda delimitado por tres fases: (i) la transformación del conjunto de datos original que se ha proporcionado en la fase de requerimientos, (ii) la medida de la complejidad de los conjuntos transformados y, finalmente, (iii) la validación de las métricas con sistemas clasificadores.

Las métricas de complejidad son una herramienta polivalente que ha sido utilizada para:

1. Predecir el error del clasificador, donde se ha hallado una relación casi lineal entre la complejidad estimada del problema con métricas de complejidad geométrica y el error cometido y

2. Caracterizar la dificultad de los problemas de clasificación y estipular un dominio de competencia de los clasificadores.

Sin embargo, este proyecto se interesa por una nueva línea que utiliza las métricas para modelar un problema y se asimila al preprocesado de la Minería de Datos o Data Mining, donde las métricas de complejidad guían la elección del sistema clasificador en problemas específicos, generando subproblemas formados gracias a la transformación de vectores de atributos. La figura 7 muestra las

diferentes fases que configuran la minería de datos, comentadas a continuación:

Figura 7. Minería de datos.

• Selección: creación del conjunto de datos o muestras sobre el cual se realiza el análisis.

• Preprocesado: limpieza de los datos preprocesando la información ruidosa, errónea, faltante e irrelevante, así como la integración de múltiples fuentes de datos en una única.

• Transformación: búsqueda de las características más significativas de los datos y la representación más adecuada para su tratamiento, como el proceso de aplanamiento.

• Minería de Datos: aplicación de diversos métodos para extraer patrones de datos.

• Interpretación y consolidación: análisis y evaluación de los patrones obtenidos para generar un modelo que permita clasificar correctamente.

En esta secuencia de operaciones, las métricas se ubican en la fase de preprocesado con el objetivo de aportar información sobre los datos para proceder a su transformación. La propuesta de este proyecto se traslada esquemáticamente a la figura 8. Se recupera el espacio de problemas reales propuesto por Tin Kam Ho, pero esta vez como instrumento para situar los problemas a estudiar. Si para su complejidad no está disponible ningún clasificador, se efectúa una serie de transformaciones para desplazar el problema hacia la región que interese.

Figura 8. Nuevo enfoque de las métricas de complejidad.

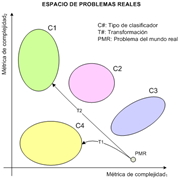
Esta metodología constituye la parte innovadora del uso de las métricas, pero el planteamiento del problema comienza por encontrar un conjunto de transformaciones del problema de la detección de cáncer de mama. Si las métricas de complejidad alcanzan una correlación lineal, se podría establecer el dominio de competencia para los clasificadores utilizados en la experimentación. En el croquis, el problema PMR se encuentra en un agujero del espacio de complejidad para el cual no existe ningún clasificador que asegure el éxito de la predicción. Entonces, aplicando las transformaciones T1 y T2, se desplaza la complejidad del problema al dominio del clasificador C4 y C1, respectivamente.

El esquema de la figura 9 resume la globalidad del proyecto con todos sus componentes y diferencia claramente los tres bloques – transformación, complejidad y validación– sobre los cuales se ha ido insistiendo.

Figura 9. Enfoque general de la transformación del problema de las mamografías según la complejidad del problema.

4.1 Transformaciones

En la extracción de atributos (tabla 1) se indica que el problema está definido por 21 atributos, pero en los conjuntos resultantes de las transformaciones no se tienen en cuenta ni la etiqueta ni la medida de

micras/píxel puesto que solamente son datos informativos que no participan propiamente en la definición de las microcalcificaciones. El objetivo de las transformaciones es aplanar cada mamografía en un único vector de atributos siguiendo dos estrategias:

1. Una única microcalcificación determina si la mamografía es cancerígena o no.

2. La globalidad de las microcalcificaciones determina si la mamografía es cancerígena o no.

4.1.1 Agrupación de todas las microcalcificaciones

En una primera aproximación no se realiza ninguna transformación y se recogen en un único conjunto todas las microcalcificaciones de las mamografías seleccionadas por el oncólogo.

4.1.2 Promedio

Esta transformación corresponde al método clásico, donde un caso sintético es la media de todos los valores de cada atributo de todas las microcalcificaciones de una mamografía.

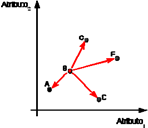
4.1.3 Centroide

De todas las microcalcificaciones de una mamografía se calcula el centroide, es decir, el punto con mínima distancia euclidiana respecto al resto. A continuación se muestra un ejemplo de localización del centroide, donde según el cálculo de distancias el punto B, con el valor más pequeño, se considera el centro del grupo (fig. 10).

E (5,4) 12.80

Figura 10. Ejemplo de centroide.

4.1.4 Valores extremos

El caso sintético queda especificado por el valor extremo del atributo seleccionado. Para identificar la malignidad de éste se ha consultado el estudio estadístico (tabla 2). [8]

Tabla 2: Valores extremos de malignidad.

ATRIBUTO	Malignidad
Área	MÍNIMO	Las microcalcificaciones pequeñas son más
		informativas en la diagnosis médica y acostumbran
		a ser más peligrosas.
Aspereza	MÁXIMO	Cuanto más rugosa y menos esférica, más
		sospechosa es.
Compacidad	MÁXIMO	Cuanto mayor es el valor, más indicios de
		malignidad. Una microcalcificación redonda tiene
		valor 1 y el índice se incrementa cuanto más
		alargada es.
Elongación del feret	MÁXIMO	Cuanto más alargada es la microcalcificación, más
		sospechosa desde un punto de vista médico.
Número de agujeros	MÁXIMO	Cuantos más agujeros presenta una
		microcalcificación, más sospechosa.

4.1.5 Aleatoria

Se selecciona de manera aleatoria una microcalcificación de cada mamografía. Se propone esta transformación como estimador de dificultad del problema. Si la métrica de complejidad asociada a esta transformación da un valor equivalente a las otras medidas puede suponer un indicio de la alta complejidad del problema y de su estructura aleatoria.

4.1.6 Conjunto reducido

Se repiten todas las transformaciones propuestas con el conjunto reducido a seis atributos: área, compacidad, número de agujeros, elongación del feret, aspereza y eje principal, que tienen un papel significativo según el artículo [9].

4.2 Métricas de complejidad

La experimentación se centra en los métodos de la familia de separación de clases y más concretamente en los de identificación mixta: boundary e intra/inter class, teniendo en cuenta que son los que mejor aproximan una relación lineal entre el error cometido por el clasificador y la métrica, como se demuestra en el estudio [3].

4.2.1 Distancia de la frontera entre clases

También conocida como boundary, surge del test propuesto por Friedman y Rafsky. Proporciona el porcentaje de nodos que conectan clases opuestas en un árbol de expansión mínimo (Minimum Spanning Tree, MST). La construcción del árbol se origina a partir del grafo que se obtiene de las relaciones de cada entrada entre ellas, mediante la distancia euclidiana. Esta métrica es un indicador de la separación de las clases y de la tendencia a los clusters. Para n puntos de entrenamiento se generan n-1 conexiones en el MST, pero el cómputo se normaliza como si fuera sobre un porcentaje de n. Cuanto mayor es el valor de la medida, más se acentúa la presencia de puntos cercanos de diferente clase. El peor caso es cuando el árbol de expansión mínimo no contiene ninguna arista que conecte dos puntos de la misma clase. Por el contrario, cuanto menor es el valor, más agrupadas están las clases y menos dificultad aparente denota el problema. Esta métrica no es adecuada para diferenciar si los problemas son linealmente separables. En el caso de dos clases considerablemente entrelazadas, la mayoría de puntos se sitúan cerca de la frontera de las clases. Lo mismo puede ocurrir en un problema linealmente separable donde los márgenes sean más estrechos que la distancia entre puntos de la misma clase.

Para obtener el mapa de conexiones binarias se transforma el grafo que generan todas las muestras en un MST mediante el algoritmo de Kruskal.

hacer

PASO 1. Calcular todas las distancias de las aristas del grafo. PASO 2. Ordenar las conexiones en sentido ascendente.

PASO 3. mientras la lista ordenada de distancias no esté vacía

3.1 Conectar los nodos de distancia mínima.

3.2 si la conexión deriva en un grafo cíclico

entonces

fmientras

3.2.1 Deshacer la conexión.

fsi

La figura 11 muestra la construcción del árbol binario. El punto de partida es un grafo con todos los nodos conectados entre ellos y a cada arista su distancia euclidiana asociada. Se empieza por ordenar las distancias de

manera creciente. El paso 1 siempre corresponde a la arista de distancia mínima, para este caso d=5. En el paso 2, la siguiente distancia a analizar es colindante con la primera y no forma ningún círculo cerrado, por lo tanto se unen. Los pasos 3 y 4 ilustran las uniones siguientes. A partir del paso 4, el resto de iteraciones tratan todas las aristas, que no prosperan porque sus conexiones derivan en grafos cíclicos.

Figura 11. Obtención del MST según el algoritmo de Kruskal.

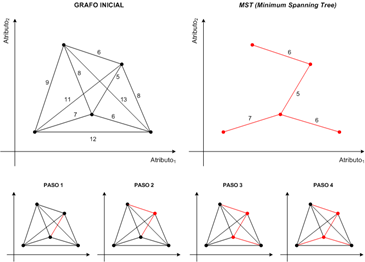
Generado el MST, se contabilizan las conexiones entre nodos de diferentes clases. En el ejemplo de la figura 12, los enlaces rojos unen clases opuestas y representan las fronteras que delimitan las agrupaciones de puntos (microcalcificaciones). En resumen, la medida se calcula como:

boundary =

3 = 0.18

17

Figura 12. Distancia de boundary.

4.2.2 Ratio entre las distancias del vecino más próximo de la misma clase y de fuera de la clase

Conocida también por intra/inter class, compara la dispersión dentro de las clases respecto a la separabilidad entre clases distintas. El cálculo se computa como:

⎛

n

⎜ådint ra

( xi, xj

) ⎞ / n

donde dintra es la mínima distancia euclidiana entre dos instancias vecinas xi y xj de la misma clase.

⎝ r =1 ⎠

dinter es la mínima distancia euclidiana entre dos

⎟

⎛

n

⎜ådint er

(xi, xj

)⎞ / n

instancias vecinas xi

y xj

de clases opuestas.

⎟

⎝ r =1 ⎠

n es el número de instancias del problema.

Se calculan las distancias euclidianas de cada punto con el vecino más próximo de su misma clase y con el de fuera de la clase. Se promedian todas las distancias del vecino más próximo entre puntos de la misma clase (intraclass) y también las distancias del vecino más próximo entre puntos de clases opuestas (interclass). La ratio de las medias constituye la métrica de complejidad. La proximidad de puntos opuestos afecta la tasa de error de un sistema clasificador k-NN. Es decir, cuanta más dispersión presenta el conjunto de datos, mayor es el error cometido por el clasificador. El valor de la medida puede ser superior a 1 si la distancia entre el vecino más cercano de la misma clase es mayor que la del vecino más cercano de la clase opuesta. Cuanto menor es su valor, más agrupadas están las instancias de la misma clase y más separadas de la clase opuesta (fig. 13)

Figura 13. Distancias entre el vecino más próximo de la misma clase y el vecino más próximo de fuera de la clase.

A continuación se muestra un ejemplo del cálculo como lo muestra la figura 14:

Figura 14. Cálculo de la intra/inter class.

4.3 Validación con clasificadores

Para llevar a cabo la validación con clasificadores se utiliza la herramienta WEKA [10]. Es un proyecto dirigido por la Universidad de Waikato de Nueva Zelanda que ofrece una colección de algoritmos de aprendizaje automático. Implementa numerosas técnicas de procesado de datos, clasificación, regresión, clustering, asociación de reglas y visualización. En este proyecto se aplican concretamente los algoritmos clasificadores IB1, IB3 y J48, este último más conocido como C4.5.

5 RESULTADOS

5.1 Métricas de complejidad

La tabla 3 resume los resultados de las dos métricas de complejidad estudiadas, el límite entre clases y la distancia intra/inter entre clases, sobre dos juegos de pruebas. La primera aproximación se efectúa sobre un conjunto de 23 atributos y la segunda sobre el conjunto reducido a 6.

Tabla 3: Resultados de las métricas de complejidad.

	23 atributos		6 atributos
	Boundary	Intra/Inter	Boundary	Intra/Inter
Promedio’	0.370	0.898	-	-
Número de agujeros	0.412	0.927	0.458	0.922
Todas	0.417	0.928	0.442	0.931
Aleatoria	0.421	0.960	0.467	0.952
Compacidad	0.423	0.966	0.472	0.914
Promedio	0.425	0.955	0.425	0.914
Aspereza	0.435	0.954	0.458	0.913
Centroide	0.439	0.971	0.481	0.953
Elongación del feret	0.458	1.005	0.425	0.927
Elongación	0.462	0.966	0.458	0.913
Área	0.523	0.979	0.513	1.007

Los valores obtenidos se sitúan en el intervalo [0.37-0.52] para la boundary y [0.89-1.00] para la intra/inter class, en ambos se destaca la poca amplitud. Esto significa que todas las transformaciones conllevan una complejidad similar. La mejor medida se consigue con la transformación del promedio facilitada con el conjunto original y para la cual se utilizan únicamente 21 atributos que no se han podido identificar (Promedio'). La peor corresponde a la área en la boundary y a la elongación del feret en la intra/inter class. Estos resultados cambian cuando se reduce el conjunto pero la área se mantiene como la peor de las transformaciones, tal y como se detectó con el conjunto de 23 atributos.

En general las dos métricas han obtenido resultados en la misma dirección, es decir que cuando la boundary predice una determinada complejidad, la métrica intra/inter class la confirma. La gráfica de la figura 15 representa la complejidad del problema sobre las dimensiones de las dos métricas: boundary e intra/inter class.

Figura 15. Complejidad del problema respecto a las métricas boundary e

intra/inter class.

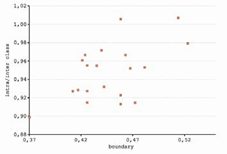
Se constata que las dos métricas de complejidad presentan un cierto grado de correlación. Esta relación también se observa en los estudios [3,7]. Además, se detecta que las medidas de las transformaciones se agrupan en círculo, delimitando un posible dominio de competencia del clasificador.

5.2 Clasificadores

Las tablas 4 y 5 presentan el porcentaje de aciertos y la raíz del error cuadrático cometido por los sistemas clasificadores IB1, IB3 y C4.5

desarrollados por el WEKA sobre los conjuntos transformados. Al igual que en las métricas de complejidad, los resultados se dividen en dos grupos.

Tabla 4: Resultados de los clasificadores para el conjunto de 23 atributos.

	IB1		IB2		IB3
	Acierto4	Error5	Acierto	Error	Acierto	Error
Promedio’	62.963	0.608	65.277	0.504	62.500	0.507
Número de agujeros	60.185	0.631	60.648	0.523	62.037	0.520
Todas	58.941	0.640	60.595	0.529	65.083	0.479
Aleatoria	57.870	0.649	60.648	0.521	54.629	0.519
Compacidad	52.777	0.687	55.092	0.568	55.555	0.566
Promedio	59.722	0.634	54.629	0.563	62.500	0.533
Aspereza	57.870	0.649	54.166	0.553	64.351	0.491
Centroide	54.166	0.677	54.166	0.555	53.240	0.533
Elongación del feret	53.240	0.683	57.870	0.551	71.296	0.452
Elongación	52.777	0.687	55.092	0.568	55.555	0.566
Área	52.777	0.687	54.629	0.554	57.407	0.519

Tal y como se intuye en los resultados de las métricas de complejidad (tabla 3), los valores obtenidos se mantienen homogéneos dentro de un estrecho intervalo [52%-65%], con la excepción del clasificador C4.5 que alcanza un acierto del 71,29% en la transformación de la elongación del feret. Por lo que respecta a los clasificadores de la familia IBk, cabe destacar la relación de la métrica de complejidad con la precisión de clasificación. La métrica de complejidad más favorable ha obtenido el mejor resultado de clasificación (Promedio’ [boundary: 0.37, intra/inter: 0.89, acierto: IB1: 62.9% IB3: 65.2% C4.5: 62.5%]) y la peor ha coincidido con uno de los resultados más bajos (Área [boundary: 0.52, intra/inter: 0.97, acierto: IB1: 52.7% IB3: 54.6% C4.5: 57.4%]).

En el segundo juego de pruebas, el porcentaje de aciertos tiende a empeorar para los IBk y mejorar para el C4.5, aunque sería necesario aplicar un test estadístico para determinar si la diferencia es significativa. El área se mantiene como la peor transformación.

Tabla 5: Resultados de los clasificadores para el conjunto de 6 atributos.

	IB1		IB3		C4.5
	Acierto	Error	Acierto	Error	Acierto	Error
Número de agujeros	56.018	0.663	56.481	0.555	64.351	0.494
Todas	55.870	0.664	57.311	0.540	65.698	0.474
Aleatoria	55.092	0.670	50.463	0.569	52.314	0.524
Compacidad	55.092	0.670	56.018	0.559	59.722	0.507
Promedio	61.111	0.623	56.481	0.436	65.740	0.489
Aspereza	60.185	0.631	54.629	0.554	63.888	0.496
Centroide	53.703	0.680	47.685	0.572	51.851	0.516
Elongación del feret	56.018	0.662	63.425	0.524	71.296	0.451
Elongación	55.092	0.670	56.018	0.559	59.722	0.507
Área	45.370	0.739	49.537	0.583	61.574	0.491

 

5.3 Análisis

Se representan gráficamente las métricas de complejidad y el porcentaje de aciertos de los tres clasificadores. (fig. 16)

Figura 16. Correlación entre el porcentaje de aciertos y la boundary.

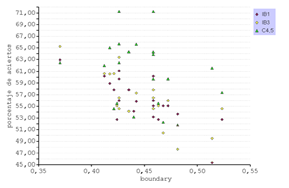
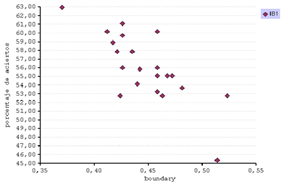
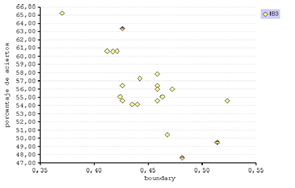
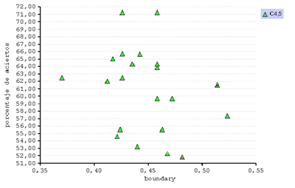
En general el C4.5 presenta una eficiencia mayor en comparación al k- NN. Esto se debe a que el algoritmo del árbol de decisión clasifica aplicando un proceso de selección de atributos discriminantes. Incluso así, este método presenta una distribución irregular pero en cambio el IB1 e IB3 se aprecian correlatos.

La representación en función del error confirma la buena correlación con el IB1 y permite observar cómo se agrupan los resultados de cada método. El comportamiento del C4.5, obteniendo una buena predicción, es errático y no ha establecido una relación con las métricas de complejidad. Inexplicablemente, en el caso de la transformación de la elongación del feret, se obtiene la mejor clasificación cuando la métrica de complejidad indica lo contrario (fig. 17).

Figura 17. Correlación entre el error del clasificador y la boundary.

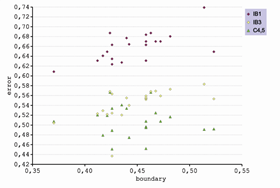
La gráfica de la figura 16 que reúne el porcentaje de aciertos y la métrica intra/inter class dibuja una tendencia lineal en los tres clasificadores, pero se identifica muy claramente para el IB1 (fig. 18).

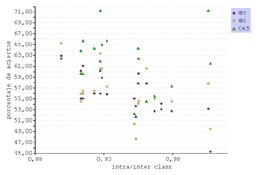
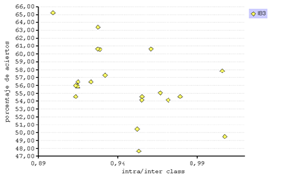
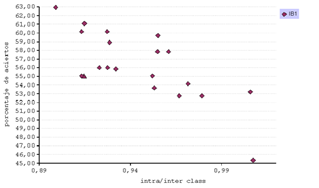
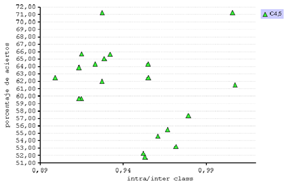
Figura 18. Correlación entre el porcentaje de aciertos y la intra/inter class.

Se recorre a la gráfica del error (fig. 17) para demostrar una relación lineal con los otros dos métodos, pero sólo se resalta en IB3. El C4.5 sigue con una oscilación variada. En este análisis también se detecta que los resultados de cada clasificador se agrupan entre ellos (fig. 19).

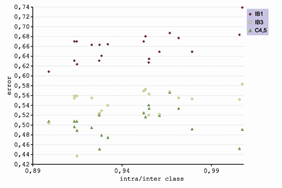
Figura 19. Correlación entre el error del clasificador y la intra/inter class.

La experimentación ha producido valores interesantes como la correlación entre métricas y la relación entre la métrica de la frontera (boundary) y el error del clasificador IB1.

5.4 Error respecto al clasificador XCS

Sobre las gráficas de la métrica boundary (fig. 16) y de la intra/inter class (fig.

19) del estudio, [3] se puede situar el problema de cáncer de mama, utilizando los resultados de la transformación Promedio’ obtenidos en este

proyecto. El error se expresa como 1-accuracy, que corresponde al porcentaje de instancias mal clasificadas y no al error cuadrático (fig. 20).

Figura 20 Porcentaje de errores cometido por el clasificador XCS según las métricas: (a) boundary e (b) intra/inter class.

Según la relación lineal, el error en la predicción que cometería el XCS sería del 24% para la boundary y del 39% para la intra/inter class, sabiendo que los valores de la métrica en la transformación son de un 37% y un 0.89, respectivamente.

Tabla 6: Resultados de la clasificación de la transformación Promedio'.

Clasificador Acierto (%) Error (%)

IB1 62.96 37.03

IB3 65.27 34.72

C4.5 62.50 37.50

Comparando el valor de la gráfica y los porcentajes de errores de la Tabla 6, se constata que la métrica intra/inter class aproxima un error de clasificación parecido al obtenido para los clasificadores IB1, IB3 y C4.5 y, justifica que esta métrica sirve de estimador del error.

6 CONCLUSIONES

Este proyecto se ha centrado en el problema de detección de cáncer de mama, una de las líneas de investigación del GRSI6. Actualmente esta enfermedad afecta un gran colectivo de mujeres y puede llegar a ser mortal. Su superación depende del estado del tumor en el momento de su detección, de aquí la insistencia en la prevención: autoexploraciones mamarias y visitas periódicas al especialista. Pero la mejor prevención es la diagnosis precoz a partir de las microcalcificaciones, un proceso que requiere el tratamiento de la imagen y la extracción de características. En esta última fase, un paciente dispone de un conjunto variable de microcalcificaciones. Esto supone un primer problema, ya que para que esta información pueda ser tratada por un clasificador debe ser sintetizada en un único caso. Hasta ahora, esta síntesis

se ha realizado promediando todas las microcalcificaciones, pero este procedimiento no tiene base teórica por lo que este proyecto intenta evaluar si hay otras transformaciones mejores que puedan aportar mayor información o por el contrario confirmar el uso de la primera.

Esta evaluación se realiza mediante métricas de complejidad. Esta parte es la más innovadora del proyecto, ya que habitualmente se evalúa si un problema se modela correctamente o no a partir del porcentaje de aciertos en la clasificación, lo cual puede estar demasiado vinculado a resultados de un clasificador en particular.

Los objetivos definidos al inicio del proyecto se engloban en tres áreas diferentes pero a la vez entrelazadas: la transformación de los datos, el cálculo de la complejidad con métricas de complejidad y la validación de los resultados aplicando sistemas clasificadores.

6.1 Transformaciones

Las transformaciones propuestas se resumen en la tabla 7:

Tabla 7: Resumen de las transformaciones propuestas.

TRANSFORMACIONES

Resumen

Todas   Promedio Centroide   Valores extremos Aleatoria

Recopila todas las microcalcificaciones presentes en una mamografía. Calcula la media de cada atributo de todas las microcalcificaciones de una mamografía. Busca la microcalcificación que constituye el centro de gravedad respecto al resto. Selecciona la microcalcificación según el valor máximo o mínimo de malignidad del atributo especificado. Escoge una microcalcificación aleatoria de cada mamografía.

Sobre los conjuntos generados de cada transformación se han aplicado dos métricas de complejidad: boundary e intra/inter class dado que en el estudio [3] muestran una relación casi lineal con el error del clasificador. Los resultados no han destacado diferencias significativas entre las transformaciones. Las métricas de boundary han oscilado entre los márgenes de [0.37-0.52] y las de intra/inter class entre los márgenes [0.89- 1.00].

En la transformación que agrupa todas las microcalcificaciones, se esperaba que las métricas revelasen la dificultad de establecer una relación entre un volumen tan grande de datos y su diagnóstico, lo que hubiera indicado la presencia de microcalcificaciones irrelevantes. Sin embargo, los resultados no han sido esclarecedores y permanece un conjunto igual de válido que los demás. Para la transformación aleatoria, los resultados obtenidos se asemejan al resto de transformaciones estudiadas, siendo un síntoma de la complejidad del problema y su posible estructura aleatoria.

Por otro lado, la experimentación se ha divido en dos partes diferenciadas por el número de atributos del conjunto de datos: uno de 23 y el otro reducido a 6 según su relevancia especificada en [9]. Teniendo en cuenta que las transformaciones propuestas no han generado resultados destacables, se confirma la complejidad del problema. En las pruebas realizadas, los valores no cambian visiblemente entre el conjunto de 23 atributos y el de 6, lo que indica que el conjunto reducido está formado por las características realmente relevantes. No obstante, el porcentaje de aciertos no es extremadamente elevado y, por lo tanto se podría interpretar que faltan otras características más significativas para incrementar la información y que podrían haberse omitido durante la selección dirigida por los oncólogos.

Finalmente, en el presente proyecto y dadas las condiciones expuestas, la transformación basada en la elongación del feret, resuelta por el C4.5, es la mejor con diferencia. Para el clasificador IBk, la transformación con mejor rendimiento es la media que se proporcionó al inicio del proyecto y que está compuesta por 21 atributos.

6.2 Métricas de complejidad

Las métricas de complejidad fijan la dificultad de la clasificación a partir de la estructura geométrica de la separación de las clases, aunque el análisis de la

complejidad de los problemas es todavía una disciplina reciente donde hay una falta de comprensión de las métricas. De hecho es difícil representar gráficamente el significado de cada métrica. Por ejemplo, determinar el porcentaje de puntos en la frontera de las clases da una idea general de la proximidad entre puntos de diferentes clases pero no necesariamente un valor elevado de ésta implica que el problema sea extremadamente complejo.

Algunas de estas métricas de complejidad se han utilizado antes, de manera separada, para caracterizar problemas de clasificación, pero hay pocos estudios sobre su efectividad. Se han obtenido métricas que son buenas para determinados tipos de conjuntos de datos como es el caso del ratio del discriminante de Fisher, útil para indicar la separación de clases que siguen una distribución de Gauss pero no para dos clases que forman anillos concéntricos, uno dentro del otro sin solaparse. Es por este motivo, que las líneas de estudio prevén que otras métricas aplicadas de manera combinada deberían ofrecer una noción más completa de la separación de las clases y de la dificultad de la clasificación.

En este proyecto, la experimentación ha revelado una correlación lineal entre la boundary y la intra/inter class. No hay que precipitarse con esta conclusión puesto que otros estudios indican que no en todos los casos se produce y podría ser fruto de resultados ad hoc al problema analizado.

También se observa que una buena métrica de complejidad no garantiza que los resultados del clasificador sean buenos, pero la premisa contraria si se cumple. Una medida mala de complejidad implica malos resultados en clasificación y por lo tanto permite descartar aquellos conjuntos de datos.

6.3 Validación de los resultados

Las primeras pruebas se han realizado con el conjunto de datos completo y los resultados han sido satisfactorios, aunque el estudio con los 23 atributos haya conseguido valores ligeramente inferiores a los del artículo [9]. Se esperaba una variación de valores superior a la obtenida, el porcentaje de aciertos se sitúa en un rango que varía entre 41 y 71% pero la gran mayoría de valores se encuentran alrededor del 55%. No son resultados muy destacables pero sí comparables a los resultados de [9]. Con el fin de extender el estudio y comprobar el comportamiento de las métricas, las transformaciones se han repetido con un conjunto reducido a 6 atributos relevantes. La relevancia de estos atributos se ha determinado a partir del análisis realizado en [9]. Los resultados han sido equivalentes y, por lo tanto se confirma que los atributos escogidos son discriminantes respecto al resto del conjunto. La experimentación se alinea con otros estudios y confirma la linealidad entre la métrica boundary y la intra/inter class. También, se puede asegurar la correlación lineal entre el error cometido y las dos métricas de complejidad con el clasificador IB1.

Este estudio revela que las métricas de complejidad sirven para predecir el error cometido por el sistema clasificador, y se desprende una futura línea de investigación acerca de la representación de la complejidad y su relación con la precisión de la clasificación.

1 Trabajo ganador de la Medalla “Hno. Salvador González 2007”, Área: Ingeniería y Tecnología, Nivel: Licenciatura, Categoría: Avanzada.”, XIVI Jornadas de Investigación, Universidad La Salle, Mayo 2007.

2 Este trabajo de investigación es fruto del Proyecto Final de Carrera (PFC), defendido el pasado 16 de octubre de 2006 en la ETSEEI La Salle, Universitat Ramón Llull.

4 Porcentaje de aciertos.

5 Raíz del error medio cuadrático.

6 Grupo de Investigación en Sistemas Inteligentes, Enginyeria i Arquitectura la Salle (Universitat Ramon Llull).

REFERENCIAS

[1] Golobardes, E. (2005). Apuntes de la asignatura de Inteligencia Artificial. Documento interno. Enginyeria i Arquitectura La Salle.

[2] Blanch Carles, M. (2004). “Detecció automàtica de microcalcificacions i grups de microcalcificacions a partir de l'anàlisi de les imatges mamogràfiques”. J. Freixenet i Bosch (dir.); D. Raba Sánchez (tut.) Proyecto final de carrera. Universitat de Girona. Escola Politècnica Superior.

[3] Bernardó Mansilla, E.; Ho, T.K. (2005). “Domain of competence of XCS classifier system in complexity measurement space". IEEE Transaction Evolutionary Computation. núm. 1, 9, 82-104.

[4] Ho, T.K. (2006). Geometrical complexity of classification problems. [En línea]. Disponible en: arxiv.org/pdf/cs.CV/0402020.

[5] Ho, T.K. (2002). ”A data complexity analysis of comparative advantages of decision forest constructors". Pattern Analysis and Applications. 5, 102-112.

[6] Ho, T.K.; Basu, M. (2002). “Complexity measures of supervised classification problems". IEEE Transaction on Pattern Analysis and Machine Intelligence, 3(24), 289-300.

[7] Ho, T.K.; Bernardó Mansilla, E. (2006). “Data complexity and domains of competence of classifiers". Pattern Recognition.

[8] Barceló, C.; Thió, S. (1997). “Estudio piloto sobre el diagnóstico de benignidad o malignidad de las microcalcificaciones mamarias mediante digitalización y análisis estadístico”. Sección de Estadística y Análisis de Datos del Departamento de I.M.A.

[9] Golobardes, E. et al. (2001). ”Classifying microcalcifications in digital mammograms using machine learning tecniques". Proceedings del 4rt Congrés Català d'Intel·ligència. 92-99.

[10] Witten, I.A.; Frank, E. (2000). Data mining. Practical machine learning tools and techniques with Java implementations. 1a ed. Morgan Kaufmann Publishers.

BIBLIOGRAFÍA

Aha, D.W.; Kibler, D.; Albaert, M.K. (1991). “Instance-based learning algorithms". Machine Learning. 6(1), 37-66.

Bernardó Mansilla, E. (2002). “Contributions to genetic based classifier systems”. Tesis doctoral. Universitat Ramon Llull. Enginyeria i Arquitectura La Salle.

Blake, C.L.; Merz, C.J. (2006). “UCI Repository of machine learning databases. 1998” [En línea]. Universitat de California. Irvine. Department of Information and Computer Sciences. Disponible en:

<http://www.ics.uci.edu/$\sim$mlearn/MLRepository.html>.

Dietterich, T.G. (1998). “Approximate statistical tests for comparing supervised classification learning algorithms". Neural Computation, 7(10), 1895-1924.

Ho, T.K. (2000). “Complexity of classification problems and comparative advantages of combined classifiers". Proc. First International Workshop on Multiple Classifier Systems. Lecture Notes in Computer science, 1857, 97-106.

Ho, T.K. (2006). Geometrical complexity of classification problems. [En línea]. Presentación PPT. Disponible en:

<www.disi.unige.it/person/MasulliF/ricerca/school2002/contributions/vietri 02-lect-ho1.pdf>.

Molina López, J.M.; García Herrero, J. (2004). Técnicas de análisis de datos. Universidad Carlos III de Madrid.

Quinlan, R. (1993). C4.5: Programs for machine learning. 1a ed. San Mateo [California]: Morgan Kaufmann Publishers, ISBN: 1-55860-238-0.

Servente, M. (2002). “Algoritmos TDIDT aplicados a la minería de datos inteligente”. Tesis doctoral, Universidad de Buenos Aires, Facultad de Ingeniería.

Wall, L. (1996). Programming Perl. 3a ed. O'reilly & associates, ISBN: 1- 56592-149-6.