Martha Buschbeck1 y Gabriel Cuevas2.
1 Escuela de Ciencias Químicas. Universidad La Salle. E mail: mebuschbeck@yahoo.de
2 Instituto de Química, Universidad Nacional Autónoma de México. E mail: gccgb@servidor.unam.mx
Recibido: Mayo 31, 2007. Aceptado: Julio 12 2007
RESUMEN
El proceso de inversión de la ciclohexanona y la 4-metilciclohexanona muestran una superficie de energía potencial similar, controlada por los metilenos de las posiciones 2 y 6, mientras que la topomerización está suprimida. La 2 y la 3-metilciclohexanona muestran superficies controladas de igual manera por los metilenos de las posiciones 2 y 6 y presentan un proceso de topomerización complejo. Debido a la baja energía de los estados estacionarios, los diferentes métodos teóricos muestran dificultad para ubicar y describir estados estacionarios, por lo que deben ser revisados. Los resultados de energías conformacionales y energías de inversión calculadas concuerdan satisfactoriamente con los resultados experimentales reportados en la literatura.
Palabras clave: topomerización, ciclohexanona, superficie de energía, energía.
ABSTRACT
Inversion process of cyclohexanon and 4-metylcyclohexanon show a similar potential energy surface controlled by methylenes of positions 2 and 6, while topomerization is suppressed. 2 and 3-metylcyclohexanon show controlled surfaces likewise controlled by methylenes of positions 2 and 6 and show a complex topomerization process. Given the low energy of stationary states, diverse theoretical methods show difficulty to locate and describe stationary states; thus, they have to be reviewed. Results of conformational energies and calculated inversion energies satisfactorily match the experimental results reported in the literature.
Key words: topomerization, ciclohexanon, energy superficie, energy.
INTRODUCCIÓN
Las moléculas no son, por lo general, estructuras planas e inmóviles como se concluye a partir de los dibujos que se suelen hacer de ellas. Son especies tridimensionales en donde los modos normales de vibración se encuentran activos debido al efecto de la temperatura. Así, los enlaces giran continuamente y ése es el campo que aborda el análisis conformacional, eje central de la presente comunicación; ya que los diferentes isómeros ocasionados por el giro de los enlaces sencillos tienen asociado un valor de energía. El análisis conformacional se ocupa del estudio de los diferentes arreglos de las moléculas originados en el giro de enlaces sencillos.
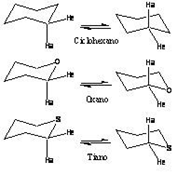
Un caso especialmente relevante para el desarrollo del análisis conformacional son los anillos de seis miembros, como el ciclohexano, oxano, tiano, etc., (esquema 1), que se caracterizan porque sus energías de inversión son elevadas respecto a anillos de otros tamaños y por lo tanto se les puede estudiar de forma tanto experimental como teórica.

El ciclohexano, de simetría D3d tiene dos conjuntos de átomos de hidrógeno geométricamente diferentes. Un conjunto de ellos es paralelo al eje S6 y se le denomina hidrógenos axiales y el otro conjunto se ubica en el “ecuador de la molécula” y se les denomina ecuatoriales. Cuando se produce la inversión, varios de los enlaces sencillos C-C de la molécula giran y los enlaces axiales adoptan la posición ecuatorial mientras que los ecuatoriales pasan a ser axiales. Esto sucede en el ciclohexano con una frecuencia de unas 100,000 veces por segundo a temperatura ambiente. [1]
La inversión de una molécula es un mecanismo conformacional caracterizado por un cambio de signo en cada uno de los ángulos de torsión que la conforman y el proceso se compone de varias etapas que determinan el progreso de dicha inversión, en las que participan estructuras de inversión. Existen también estructuras intermedias, llamadas topómeros, que sufren intercambio en la posición de enlaces idénticos y que generan el proceso de topomerización. La topomerización de una molécula se distingue por convertir a dicha molécula en otra que es superponible con la molécula original, pero en la cual dos o más átomos o ligantes han intercambiado lugares. [2]
La conformación silla del anillo de seis miembros (esquema 1) para el ciclohexano es lo suficientemente estable debido a que la tensión angular es nula por mantener un valor tetraédrico en sus ángulos, haciéndola muy abundante en la naturaleza, y es debido a su movilidad conformacional que se observa la inversión. [2] Este proceso se ha establecido mediante numerosos estudios de resonancia magnética nuclear dinámica y espectroscopía infrarroja, así como cálculos de campos de fuerza. En 1985, en un estudio basado en mecánica molecular llevado a cabo por Kolossvary y Guida, [3] se hizo evidente que la inversión es un proceso independiente de la topomerización, involucrando varios pasos intermedios, produciéndose primero un máximo energético con conformación de media silla que, en un segundo paso isoenergético, con el primero la invierte. [4]
La importancia de la descripción del proceso de inversión para este primer sistema anular radica en que ha servido como base para el estudio de otros anillos de seis miembros con diferentes sustituyentes, cuya conformación influye en diversos fenómenos de la química orgánica y bioorgánica relacionados con mecanismos de reacción y procesos de reconocimiento molecular. [4]
En los libros de texto de análisis conformacional se suele presentar el proceso de inversión de este tipo de anillos indicando la existencia de un intermediario en el proceso al que se le llama bote torcido. También el proceso describe la existencia de botes y semisillas, que son requeridas para establecer el mecanismo de inversión. En el esquema 2 se muestran algunos confórmeros análogos al del ciclohexano cuando un metileno se sustituye por oxígeno.
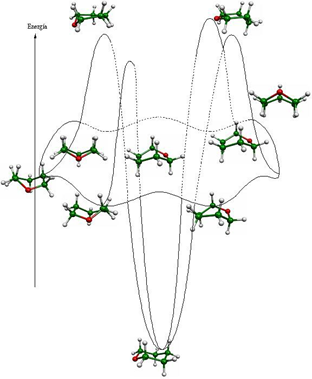
Debido a que se puede demostrar que el mecanismo de inversión está sujeto a los mismos principios a los que están sujetos los mecanismos de reacción, es posible describirlos en forma rigurosa, por lo que es necesario describir los dos mínimos energéticos asociados a cada estado de transición. Ésta es la razón del por qué los esquemas descritos en los textos comunes de análisis conformacional son imprecisos. [1,2]
Como parte del estudio de las propiedades conformacionales de los anillos base de los carbohidratos, recientemente se describió en forma rigurosa la superficie de energía potencial del ciclohexano, oxano, tiano, [4,5] y su correspondiente sulfona. [6] Una superficie de energía potencial está definida por tres ejes; dos de ellos formados por coordenadas de variables termodinámicas independientes denominadas grados de libertad y el otro por una variable dependiente que representa la energía total de la molécula.
Al parecer el comportamiento conformacional es similar entre los anillos de seis miembros aunque hay aspectos que aún no se conocen bien, como los factores que estabilizan ciertos estados de transición. El contribuir al conocimiento de estos factores es el objeto del presente artículo, por lo que se aborda un sistema carbocíclico, la ciclohexanona, que es un compuesto cíclico de seis miembros con un grupo carbonilo y que tiene fórmula molecular C6H10O. La conformación más estable de este sistema es la silla que presenta el ángulo C-C(O)-C de 115.3°, [7] debido a la hibridación sp2 del carbonilo. Se ha calculado que el confórmero bote torcido de la ciclohexanona tiene una energía de 2.72 kcal/mol mayor que la de la silla y que la energía de activación experimental para la inversión es de 4.0 kcal/mol, [8] que es considerablemente menor que la del ciclohexano, cuya energía de activación es de alrededor de 10.5 kcal/mol. [9]
A pesar de la relevancia del estudio de este compuesto por ser clave en el desarrollo del análisis conformacional y por servir como punto de referencia para otros compuestos, [8] hasta la fecha no se han establecido los confórmeros implicados en el proceso de inversión para la ciclohexanona ni para sus tres derivados monometilados, por lo que tampoco se conoce el cambio energético de las moléculas durante las diferentes etapas del proceso. Por esta razón, en el presente trabajo se estudió de manera rigurosa la superficie de energía potencial del proceso de inversión de la ciclohexanona y de los isómeros 2-, 3- y 4-metilciclohexanona.
Un aspecto que vale la pena destacar con fines aclarativos es el hecho de que muchas de las conformaciones que puede adquirir una molécula no corresponden a mínimos energéticos, y aquéllos que sí lo son se denominan isómeros conformacionales o confórmeros. Un isómero conformacional es un tipo de estereoisómero (isómeros de constitución idéntica, pero que se diferencian en el arreglo de sus átomos en el espacio) que difiere en su o sus ángulos de torsión. [2] En términos de la conformación o conformaciones de las moléculas, es posible interpretar o predecir sus propiedades físicas y químicas, así como su contenido energético. [2] A este estudio se le conoce como análisis conformacional.
La química computacional permite analizar los mecanismos conformacionales a través de las propiedades electrónicas de los estados de transición, pues dado que son estados estacionarios en la superficie de energía potencial, es posible abordarlos en forma similar a los mínimos, lo que la hace una herramienta fundamental.
METODOLOGÍA
Para determinar la secuencia y/o secuencias posibles de los procesos completos de inversión y de topomerización y realizar una descripción precisa de la geometría y energía asociadas a cada estado estacionario de estos sistemas, se realizó la optimización geométrica de los principales confórmeros de cada compuesto, seguido del análisis de los modos normales de vibración y la obtención de la energía total de cada uno de dichos confórmeros buscando todos los estados de transición, así como mínimos energéticos involucrados en dichos procesos a través de las coordenadas intrínsecas de reacción (IRC, por sus siglas en inglés), utilizando el funcional de intercambio de Becke y el funcional de correlación de Lee-Yang-Parr ajustado por una ecuación de 3 parámetros (B3LYP). En algunos casos se recurrió al método MP2 (operador de perturbación Möller- Plesset, denotado como la teoría MPn). Para ambos casos se empleó la base 6- 31G(d,p), que es una base doble ξ de valencia dividida que incluye polarización en los átomos pesados y ligeros. [10]
Con base en los principales arreglos conformacionales para los estados de transición (semisilla, bote y bote torcido) y para mínimos energéticos (silla y bote torcido) de la ciclohexanona, se buscó el arreglo más próximo a éstos con el visualizador Gauss-View, [11] y se optimizaron todos los estados de transición pertinentes para cada sistema; se calculó la energía total de cada confórmero, así como sus frecuencias vibracionales verificando que correspondieran, ya sea a estados de transición (puntos de silla con una frecuencia imaginaria) o a mínimos energéticos (índice de punto crítico igual a cero).
Posteriormente, se procedió a interconectar a cada estado de transición con sus dos correspondientes mínimos energéticos a través del cálculo de las IRC. Éstas definen puntos sobre las coordenadas de reacción en función de la longitud de la curva hasta dicho punto y el ángulo que forma la tangente a ese punto con respecto al eje X en la superficie. Para este cálculo se definió un número de puntos en cada dirección de la trayectoria de reacción, que no siempre coincide con el mínimo energético en cada lado de ésta, de modo que al terminar el cálculo de IRC se optimizó la estructura buscando un mínimo energético en la superficie y verificando su naturaleza por medio del cálculo de frecuencias (cero frecuencias imaginarias para puntos de mínima energía).
Finalmente, se realizó la interconexión de cada uno de los estados estacionarios procesados para establecer la superficie de potencial que describe a cada sistema. Para la obtención de las propiedades moleculares y coordenadas de reacción se ocupó el programa de química computacional Gaussian 94 [12] y/o Gaussian 03. [13]
Para conseguir todos los resultados que se presentan en este trabajo se utilizaron tres computadoras: estación de trabajo ocupada para visualización tipo O2 con procesador MIPS R5000, estación de trabajo ocupada para procesamiento de cálculos tipo Origin 200 con cuatro procesadores MIPS R12000, y dos estaciones de trabajo ocupadas para procesamiento de cálculos tipo Altix 350 con dos procesadores Itanium 2 cada una.
RESULTADOS Y DISCUSIÓN
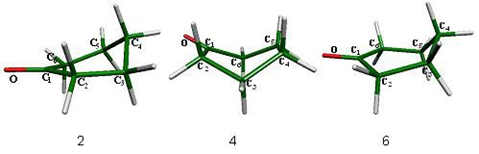
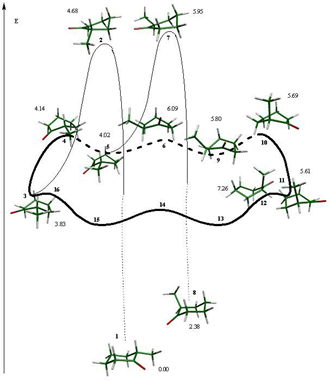
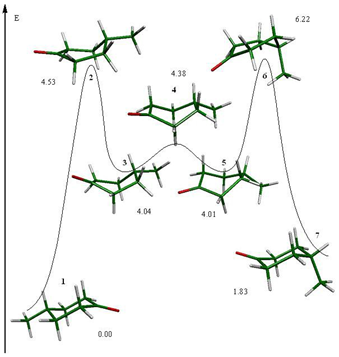
Para el proceso de inversión topomerización de la ciclohexanona se encontraron tres estados de transición diferentes (fig. 1), de los cuales, las semisillas 2 y 6 son parte del proceso de inversión y el bote 4 pertenece al proceso de topomerización. Estos estados estacionarios se muestran en la figura 1.
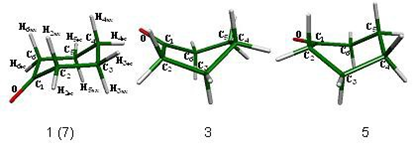
Asimismo existen tres mínimos energéticos en el proceso, la silla 1 que es idéntica a la silla 7 y dos botes torcidos (3 y 5) que están interconectados por el bote 4. Los cuatro mínimos en la superficie se presentan en la figura 2.
Como resultado de los estados estacionarios ubicados, se preparó el esquema 3 en donde se presenta la inversión de la ciclohexanona.
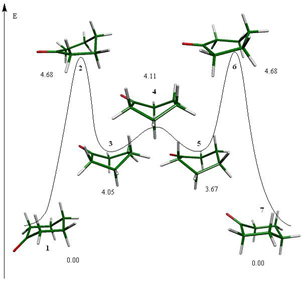
diferencias de energía (kcal/mol) con respecto al confórmero de mínima energía.
La silla 1 tiene una energía potencial de -309.90523 Hartrees y es el arreglo conformacional más estable para esta molécula, por lo que este valor de energía será utilizado para calcular la diferencia energética (ÄE) de todos los confórmeros asociados a este sistema (véase esquema 3).
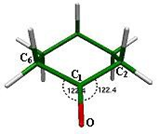
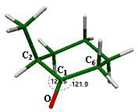
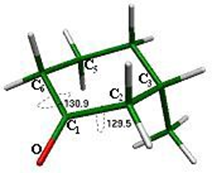
Los ángulos que forma el grupo carbonilo en este confórmero son O-C1-C6 = 122.4° y O-C1-C2 = 122.4°, valores muy cercanos a los 120°, que normalmente se presentan en la hibridación sp2 del carbonilo y son de igual magnitud por tratarse de una molécula
simétrica (fig. 3).
En el caso del ciclohexano, debido a la tensión anular, los ángulos de torsión para los hidrógenos del anillo sufren una desviación pequeña con respecto a los 60° óptimos que se observan en el propano, [14] reportándose ángulos de torsión Hec-C-C-Hax = 54.9°, Hec- C-C-Hec = 65.1° y C-C-C-C = 54.9°. En el caso de la ciclohexanona, se espera una desviación aún mayor, originada por la hibridación sp2 del grupo carbonilo encontrándose los ángulos de torsión H3ec-C3-C2-H2ax = 56.1°, H3ec-C3-C2-H2ec = -63.0°, C4-C5-C6-C1 = -51.6°. En estos datos, se observa que el grupo carbonilo obliga al ángulo de torsión formado por los carbonos C4-C5-C6-C1 a cerrarse. En un centro tetraédrico, cuando se cierra el ángulo C-C-C-C, obliga a la apertura del ángulo formado por los hidrógenos axial y ecuatorial enlazados a carbonos adyacentes con el ángulo de torsión H3ec-C3-C2-H2ax; que a su vez hace que el ángulo de torsión entre hidrógenos ecuatoriales H3ec-C3-C2-H2ec se cierre y así quedan alternados los cambios en la magnitud de estos ángulos.
Algunos ángulos de torsión formados por átomos que cambian notablemente su arreglo geométrico durante el primer proceso conformacional para la inversión en este sistema son O-C1-C2-C3 = 132.2° y O-C1-C6-C5 = -132.2°, los cuales muestran la simetría de la silla 1 (fig. 4).
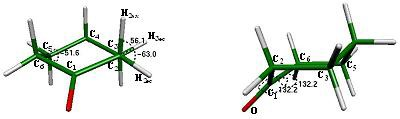
Figura 4. Ángulos de torsión H3ec-C3-C2-H2ax = 56.1°, H3ec-C3-C2-H2ec = -63.0° C4-C5-C6-C1 = -51.6°, O-C1-C2-C3 = 132.2° y O-C1-C6-C5 = 132.2°
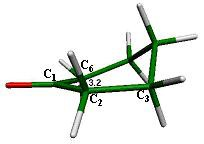
En esta superficie de energía potencial existe un estado estacionario a 4.68 kcal/mol por arriba de la silla, que corresponde a la semisilla 2 (fig. 5). Los datos que se han obtenido de manera experimental establecen una energía de inversión de 4.0 kcal/mol, [8] valor próximo al obtenido en el presente trabajo.
Normalmente, los estados de transición de inversión presentan un segmento aplanado como se observa en el ángulo de torsión C6-C1-C2-C3 = 3.2°, donde estos átomos se ubican en el plano de la molécula.
La frecuencia imaginaria de este estado de transición es de -102.79 cm-1 en donde el grupo que controla la inversión es el metileno C6 con vibración por arriba y abajo del plano, lo que obliga a la redistribución del resto de los átomos de la molécula en sentido opuesto, de tal manera que si C6 se dirige hacia abajo del plano, los dos carbonos adyacentes lo hacen hacia arriba para generar un bote torcido. De suceder lo opuesto el sistema evoluciona para generar la silla 1 ya descrita.
La secuencia que siguen los confórmeros y estados de transición en el proceso de inversión de la ciclohexanona es: la silla 1 que es el mínimo global del sistema, continuado por el estado de transición que promueve la inversión del ciclo, la semisilla 2, que conduce a un bote torcido que es un mínimo en la superficie y forma parte del proceso de topomerización y el cual está conectado a otro bote torcido (5) a través de un estado de transición, el bote 4. Finalmente el bote torcido 5 lleva a otro estado de transición de inversión que conecta con la silla 7, que es el confórmero invertido de la silla
Las diferencias energéticas con respecto al mínimo energético del sistema, la silla 1, para todos los confórmeros que componen el proceso se muestran en el esquema 3.
En el esquema 4 se presenta la inversión topomerización de la 2-metilciclohexanona. La silla en la que el grupo metilo se localiza en posición ecuatorial es el mínimo global, siendo el confórmero axial 2.38 kcal/mol menos estable al nivel de teoría B3LYP/6- 31G(d,p). Algunos resultados experimentales publicados indican que la preferencia conformacional de la 2-metilciclohexanona es de 1.58, [15] 2.16, [16] 1.57, [17] 1.8 [18] y 1.33 [19] kcal/mol y los resultados reportados en la literatura obtenidos por métodos de mecánica molecular y ab initio son de 2.92 y 2.38 respectivamente, [15] por lo que el valor encontrado en el presente trabajo está en concordancia con publicaciones anteriores.
La energía resultante del cálculo de energías a nivel B3LYP para el confórmero silla ecuatorial de la 2-metilciclohexanona tiene un valor de –349.22393 Hartrees; este valor será utilizado como referencia para la obtención de las diferencias energéticas (ÄE) del resto de los confórmeros que constituyen todas las etapas del proceso, ya que resultó ser el mínimo global del sistema (véase esquema 4).
Los ángulos que forma el grupo carbonilo en este confórmero son O-C1-C6 = 122.1° y O-C1-C2 = 122.5°, valores muy cercanos a los 120° que se presenta normalmente en la hibridación sp2 del carbonilo (fig. 6). Por otro lado, los ángulos que forman los carbonos
adyacentes, es decir, en posición a al grupo carbonilo, son cercanos al valor del ángulo tetraédrico para los carbonos sp3 de 109.2° con valores de C1-C2-Cme = 112.2° y C1-C6- H6eq = 108.4°, aunque se observa una ligera deformación en la que el ángulo que se forma con el sustituyente metilo es mayor, obligando al ángulo formado por los átomos C1-C6-H6eq a cerrarse; esto debido posiblemente a la presencia del sustituyente, aunado al efecto Thorpe-Ingold, el cual establece que en un carbono tetraédrico, cuando el ángulo entre un par de sustituyentes se distorsiona en un sentido, el ángulo formado por el otro par de sustituyentes se distorsionará de manera opuesta; [20,21] es decir, si un ángulo se abre, el otro deberá cerrarse.
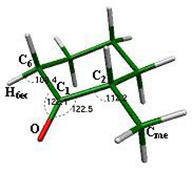
C1-C6-H6eq = 108.4° del confórmero silla ecuatorial 1 de la 2-metilciclohexanona.
Los ángulos de torsión formados por los átomos que rigen el proceso de inversión de la silla ecuatorial 1 son O-C1-C2-C3 = 129.1° y O-C1-C6-C5 = -128.4° como se muestra en la figura 7.
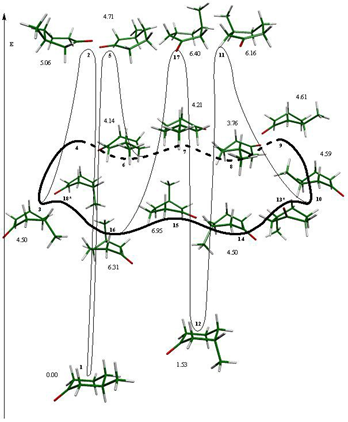
La silla 1, (con el grupo metilo en posición ecuatorial) es el confórmero más estable del sistema y está interconectada por medio de la semisilla 2 (fig. 8) con el confórmero de topomerización bote torcido 3; el proceso de topomerización está compuesto por 4 estados de transición, los botes 4, 6, 10 y 12, y por 4 mínimos en la superficie de potencial: los botes torcidos 3, 5, 9 y 11. De estos mínimos energéticos, los botes torcidos 3 y 5 generan los dos estados de transición semisillas 2 y 7, asociados a la inversión del ciclo y que están conectados con las sillas 1 (sustituyente en posición ecuatorial) y 8 (sustituyente en posición axial) respectivamente, como se observa en el esquema 4. Cabe señalar que no todos los confórmeros de topomerización esperados pudieron ser calculados al nivel de energía B3LYP/6-31G(d,p), quedando sin interconexión dentro del proceso de topomerización los estados estacionarios 3 y 12.
La inversión de este derivado se lleva a cabo cuando se supera la barrera energética de 4.68 kcal/mol, que es ligeramente mayor que la requerida para la inversión de la ciclohexanona y ésta sucede a través de los estados de transición de inversión semisilla 2 que interconecta a la silla 1 y al bote torcido 3 y de la semisilla 7 que interconecta al bote torcido 5 y a la silla 8 (fig. 8). Es importante hacer notar, según mostraron los modos vibracionales calculados, que son el carbono 2, enlazado al sustituyente metilo, y el carbono 6, los que controlan el proceso de inversión para los casos de ambas semisillas.
Las diferencias de energía con respecto al mínimo global de todos los estados estacionarios que componen el proceso se muestran en el esquema 4.
f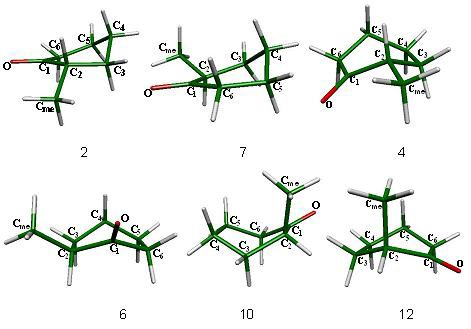
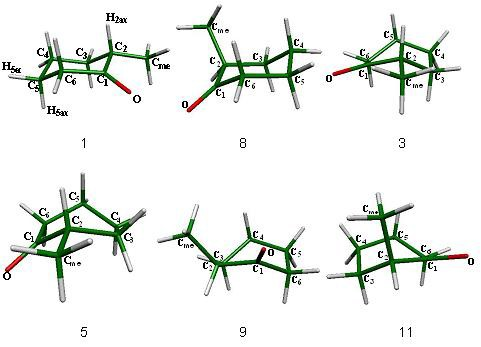
Figura 9. Mínimos en la superficie sillas 1 y 8 y botes torcidos 3, 5, 9 y 11 de la 2-metilciclohexanona.
La silla axial 8, con una energía potencial de -349.22014 Hartrees tiene una ÄE de
2.38 kcal/mol con respecto al confórmero 1. Esta energía está de acuerdo con el valor descrito en la literatura. [15] Una diferencia de 2.38 kcal/mol no es despreciable, y equivale a una proporción de entre 95 y 99% del confórmero ecuatorial en el equilibrio a una temperatura de 25°C.
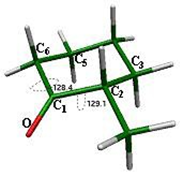
En el caso de la silla 8 con el sustituyente en posición axial, se cumple también con el valor de los ángulos de la hibridación sp2 del grupo carbonilo: O-C1-C2 = 121.6° y O-C1- C6 = 121.9° (fig. 10).
c. 3-metilciclohexanona
En el esquema 5 se presenta la inversión topomerización de la 3-metilciclohexanona. Al igual que en el sistema 2-metilciclohexanona, la silla en la que el grupo metilo se localiza en posición ecuatorial es el mínimo global, siendo el confórmero axial menos estable por 1.53 kcal/mol. En diferentes publicaciones se ha reportado que el valor del ÄH obtenido de manera experimental para este compuesto tiene valores de 1.1, [18] 1.55 [22], 1.35, [23] 1.31 [16] y 1.30 [15] kcal/mol; así mismo, en un cálculo hecho con mecánica molecular se obtuvo un valor de 1.37 kcal/mol y el resultado a nivel B3LYP/6-31G (d,p) reportado en aquella ocasión fue de 1.53 kcal/mol, [15] que es el mismo para la diferencia energética entre los dos confórmeros más estables obtenida en el presente trabajo.
Los confórmeros que forman parte del proceso de inversión topomerización de la 3- metilciclohexanona se presentan en las figuras 11 y 12.
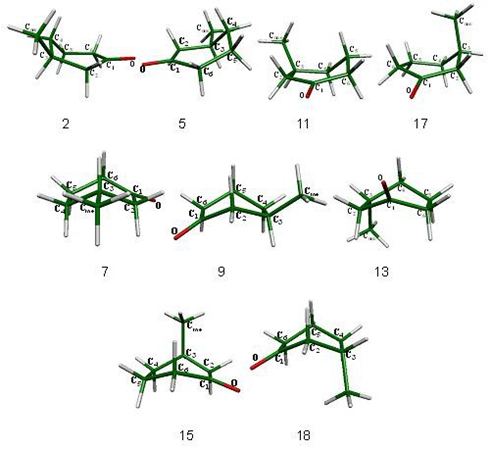
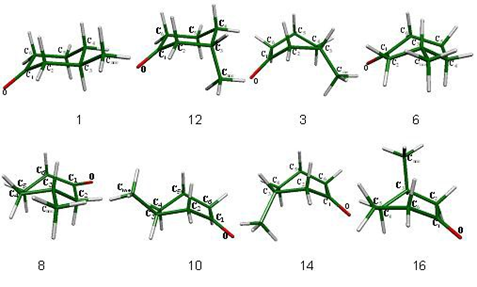
Figura 12. Mínimos en la superficie sillas 1 y 12 y botes torcidos 3, 6, 8, 10, 14 y 16 de la 3-metilciclohexanona.
La silla ecuatorial del confórmero 3-metilciclohexanona tiene una energía potencial de -349.22331 Hartrees, valor que será utilizado para obtener la diferencia energética de todos los confórmeros que participan en la inversión (véase esquema 5). Los ángulos de torsión que caracterizan a la silla con el sustituyente metilo en posición 3 ecuatorial son O-C1-C2-C3 = 131.2°, O-C1-C6-C5 = -131.9° y Cme-C3-C2-C1 = 176.7°. El ángulo de torsión
que forma el oxígeno con respecto a los carbonos C3 y C5 es de alrededor de los 130° como se ha observado en los derivados monometilados de la ciclohexanona estudiados en el presente trabajo, debido a la hibridación sp2 del grupo carbonilo.
Aunado a que los cicloalcanos presentan una tensión angular en la conformación tetraédrica de los carbonos que constituyen el ciclo, es posible que la hibridación sp2 del carbono C1 ocasione un cambio en el ángulo torsional del sustituyente metilo con respecto a los hidrógenos unidos al carbono adyacente al metino que lo soporta gracias a
|
entre el hidrógeno axial de la posición dos (H 2ax) y el carbonilo, observándose los ángulos de torsión Cme-C3-C2-H2ax y Cme-C3-C2-H2ec con valores de -57.6° con respecto al hidrógeno axial H2ax, y de 60.9° con respecto al ecuatorial H2ec como se observa en la figura 13. Sin embargo, estos valores están dentro del rango que ubica a este metilo en la posición ecuatorial para los confórmeros silla en cicloalcanos. [2]

del confórmero silla ecuatorial (1) de la 3-metilciclohexanona.
La silla ecuatorial se asocia a dos puntos de silla de la superficie de potencial que describen la geometría de las dos semisillas 2 y 6. La barrera energética del confórmero silla ecuatorial para comenzar el proceso de inversión es de 5.06 kcal/mol o de 4.71 kcal/mol para llegar a los estados de transición semisilla 2 y semisilla 5, respectivamente.
La silla axial 12 tiene una energía de -349.22088 Hartrees y una diferencia de 1.53 kcal/mol que representa entre el 5 y el 10% de ésta con respecto al isómero más estable.
Los ángulos de torsión que caracterizan a la silla con el sustituyente metilo en posición 3 axial son O-C1-C2-C3 = 129.5°, O-C1-C6-C5 = -130.9°. El ángulo de torsión que forma el oxígeno con respecto a los carbonos C3 y C5 es también de alrededor de los 130° como sucedió en el caso del confórmero ecuatorial correspondiente, y es causado de igual manera por la hibridación sp2 del grupo carbonilo. Estos ángulos de torsión se encuentran desplazados en el mismo sentido que los ángulos correspondientes en la silla ecuatorial, es decir, el ángulo de torsión O-C1-C2-C3, que se encuentra más alejado del metino C3 para el confórmero con sustituyente ecuatorial es de 131.9°, y el ángulo formado por los átomos más cercanos al metino que soporta al sustituyente metilo O-C1- C6-C5 es de -131.2°. Esto podría deberse a que el sustituyente ocasiona que el ángulo de torsión sobre el que influye se cierre, produciendo en consecuencia la apertura del ángulo opuesto.
Este confórmero está interconectado a través de las semisillas 11 y 17 con los botes torcidos 10 y 16, respectivamente (fig. 14).
En este sistema, al igual que ha sucedido en los sistemas descritos anteriormente, los carbonos que rigen el proceso son los que se encuentran en posición alfa al carbonilo, es decir, los metilenos C2 para las semisillas 2 y 11 y C6 para las semisillas 5 y 17.
El bote torcido 3 no pudo interconectarse con el bote torcido 6, ya que el bote que se esperaba en función de la razón de cambio entre los ángulos de ambos botes torcidos no pudo determinarse a ninguno de los dos niveles de teoría empleados. La secuencia de los confórmeros dentro del proceso de topomerización son botes torcidos 6 y 8 interconectados por medio del bote 7, botes torcidos 8 y 10 interconectados a través de bote 9, botes torcidos 10 y 14 interconectados por el bote 13, el cual únicamente logró optimizarse con el método MP2. Los botes torcidos 14 y 16 están asociados al bote 15 y finalmente los botes torcidos 16 y 3 están interconectados por medio del bote 18 que al igual que el bote 13 únicamente se encontró a nivel MP2. Las diferencias energéticas con respecto a la silla 1 (mínimo global), para todos los confórmeros que componen el proceso se muestran en esquema 5. En el caso de los botes 13 y 18 no es posible hacer una comparación entre su valor de energía y el valor correspondiente al mínimo global ya que están calculados a un nivel de cómputo diferente.
En el esquema 6 se presenta la inversión topomerización de la 4-metilciclohexanona. La silla en la que el grupo metilo se localiza en posición ecuatorial es el mínimo global, siendo el confórmero axial 1.83 kcal/mol menos estable. Los resultados experimentales publicados indican que este valor es de 2.10 ± 0.20 kcal/mol, mientras que otros datos obtenidos por métodos teóricos reportan valores de 1.67 kcal/mol para MMX, 1.87 kcal/mol para MM3 y 2.00 kcal/mol para B3LYP/6-31G(d), los cuales son muy cercanos al obtenido al nivel de teoría ocupado en el presente trabajo. [24]
El proceso de inversión del derivado 4-metilciclohexanona es muy parecido al proceso de inversión de la ciclohexanona observándose nuevamente que los átomos que controlan el proceso son los que se encuentran adyacentes al grupo carbonilo como se describirá más adelante.
La silla ecuatorial 1 tiene una energía potencial de -349.22303 Hartrees, valor que será utilizado para obtener la diferencia energética de todos los confórmeros que participan en la inversión (ver esquema 6). Los ángulos de torsión que caracterizan a este arreglo conformacional en el que el metilo se encuentra en posición axial son los hidrógenos enlazados a los metilenos adyacentes al metino que soporta al sustituyente Cme-C4-C3-H3ax = -59.2°, Cme-C4-C3-H3ec = 57.1°, Cme-C4-C5-H3ax = 59.2°, Cme-C4-C5-H3ec = -57.1°, ya que sus valores son muy cercanos a los valores indicados para la relación equivalente en los hidrógenos axiales y ecuatoriales del ciclohexano que son de 54.9° para hidrógeno ecuatorial con respecto a hidrógeno axial y 65.1° para hidrógeno ecuatorial con respecto al hidrógeno ecuatorial adyacente. [2]
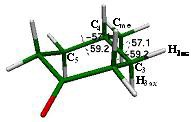
Figura 15. Ángulos de torsión Cme-C4-C3-H3ax = -59.2°, Cme-C4-C3-H3ec = 57.1°, Cme-C4-C5-H3ax = 59.2°, Cme-C4-C5-H3ec = -57.1°
La silla axial 7 por su parte tiene una energía de -349.22012 Hartrees y ÄE de 1.83 kcal/mol, que equivale a una proporción del 1 al 5% de ésta con respecto a su isómero ecuatorial. [1]
Los ángulos que caracterizan a la silla axial son los que relacionan al sustituyente metilo axial con los hidrógenos enlazados al metileno vecino (fig. 15). Los valores de estos ángulos de torsión son Cme-C4-C3-H3ax = 168.1° y Cme-C4-C3-H3ec = 51.8°, relación de valores muy parecida a la reportada para los hidrógenos en el ciclohexano de 174.9° entre hidrógenos axiales y 54.9° entre un hidrógeno axial y uno ecuatorial.
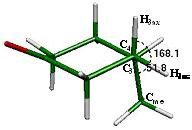
Este sistema tiene una secuencia de inversión similar a la de la ciclohexanona, observándose mejor en este sistema el cambio en la posición del sustituyente de la posición ecuatorial a la posición axial. De igual forma, en este sistema se cumple el hecho de que los átomos que controlan el proceso de inversión son los que se encuentran en posición alfa al carbonilo, es decir, los metilenos C2 y C6, como se observa en los modos vibracionales calculados para los máximos de inversión, las semisillas 2 y 6 y no participa el metino que soporta al metilo. Los confórmeros que integran el proceso de inversión de la 4-metilciclohexanona se muestran en las figuras 17 y 18.
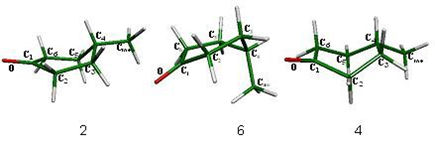
Figura 18. Confórmeros silla 1, botes torcidos 3 y 5 y silla 7.
CONCLUSIONES
Los cálculos a nivel B3LYP/6-31G(d,p) y MP2/6-31G(d,p) permiten reproducir satisfactoriamente tanto las barreras conformacionales como la diferencia en energía conformacional de la ciclohexanona y de sus tres derivados monometilados. En principio se esperaría que los grupos metileno y el mismo grupo carbonilo pudieran participar en el proceso de inversión de las ciclohexanonas estudiadas aquí; sin embargo, como se analizó en cada uno de los casos de inversiones se encontró que únicamente participan los metilenos adyacentes al grupo carbonilo. Aún cuando se buscó optimizar conformaciones en las que el carbono con el sustituyente o el grupo carbonilo pudieran regir la inversión, no se encontraron estos estados estacionarios para ninguno de los sistemas estudiados, contrastando estos esquemas generales de inversión con los reportados anteriormente, en los que el heteroátomo de la posición 1 y el metileno de la posición 4 controlan el proceso de inversión. [5]
Los métodos teóricos no permitieron encontrar todos los estados estacionarios esperados para la 2 y 3-metilciclohexanona. Esto implica serias limitaciones en los métodos teóricos empleados y sería conveniente estudiar los procesos a un nivel de teoría que represente de manera más adecuada el comportamiento de todos los sistemas. Una propuesta para mejorar la descripción de estos dos sistemas es ocupar el método MP2 para la búsqueda de todos los confórmeros que participan en el proceso de inversión, ya que este método describe las interacciones electrónicas de mejor forma, y se vio que funcionó para encontrar algunos de los estados de transición que no fue posible optimizar a nivel B3LYP como en el caso de confórmeros 13 y 18 pertenecientes al proceso de inversión-topomerización de la 3-metilciclohexanona.
REFERENCIAS
[1] Juarista, E. (1998). Introducción a la estereoquímica y al análisis conformacional, Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, México.
[2] Eliel, E., Wilen, S. (1994). Stereochemistry of Organic Compounds, John Wiley & Sons, Inc., E.U.A.
[3] Kolossvary, I., Guida, W. C. (1993). J. Am. Chem. Soc., 115, 2107.
[4] Fernández-Alonso, M. C., Cañada, J., Jiménez-Barbero, J., Cuevas, G. (2005). Chem. Phys. Chem., 6, 671.
[5]. Fernández-Alonso, M. C., Asensio, J. L., Cañada, F. J., Jiménez-Barbero, J., Cuevas, G. (2003). Chem. Phys. Chem., 4, 754.
[6] Notario, R., Roux, M. B., Cuevas, G., Cárdenas, J., Leyva, V., Juarista, E. (2006). J.
Phys. Chem. A, 110 7703.
[7] Pillen, J., Geise, H. J. (1980). Journal of Molecular Structure, 69, 137.
[8] Anet, F. A. L., Cheng, A. K., Jostein, Krane. (1973). J. Am. Chem. Soc., 95:13, 4423.
[9] Anet, F. A. L., Bourn, A. J. R. (1967). J. Am. Chem. Soc., 89:4, 760.
[10] Cuevas, G., Cortés, F. (2003). Introducción a la Química Computacional, Fondo de Cultura Económica, México.
[11] Dennington II, R., Keith, T., Millam, J., Eppinnett, K., Hovell, W. L., Gilliland, R. (2003). GaussView, Version 3.09, Semichem, Inc., Shawnee Mission, KS.
[12] Frisch, M. J., Trucks, G. W., Schlegel, H. B., Gill, P. M. W., Johnson, B. G., Robb, M.
A. J., Cheeseman, R., Keith, T., Petersson, G. A., Montgomery, J. A., Raghavachari, K., Al-Laham, M. A., Zakrzewski, V. G., Ortiz, J. V., Foresman, J. B., Cioslowski, J., Stefanov,
B. B., Nanayakkara, A., Challacombe, M., Peng, C. Y., Ayala, P. Y., Chen, W., Wong, M. W., Andres, J. L., Replogle, E. S., Gomperts, R., Martin, R. L., Fox, D. J., Binkley, J. S., Defrees, D. J., Baker, J., Stewart, J. P., Head-Gordon, M., Gonzalez, C., Pople, J. A. (1995). Gaussian 94, Revision D.4, Gaussian, Inc., Pittsburgh, PA., E.U.A.
[13] Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Montgomery, Jr., J. A., Vreven, T., Kudin, K. N., Burant, J. C., Millam,
J. M., Iyengar, S. S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson, G. A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J. E., Hratchian, H. P., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Ayala, P. Y., Morokuma, K., Voth, G. A., Salvador, P., Dannenberg, J. J., Zakrzewski, V. G., Dapprich, S., Daniels, A. D., Strain, M. C., Farkas, O., Malick, D. K., Rabuck, A. D., Raghavachari, K., Foresman, J. B., Ortiz, J. V., Cui, Q., Baboul, A. G., Clifford, S., Cioslowski, J., Stefanov, B. B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R. L. D., Fox, J., Keith, T., Al-Laham, M. A., Peng, C. Y., Nanayakkara, A., Challacombe, M., Gill, P. M. W., Johnson, B., Chen, W., Wong, M. W., González, C., Pople, J. A. (2004). Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT., E.U.A.
[14] Dunitz, J. D. (1970). Journal of Chemical Education, 47(7), 488.
[15] Abraham, R. J., Chadwick, D. J., Griffiths, L., Sancassan, F. (1980). J. Am. Chem. Soc., 102, 5128.
[16] Cotterill, W. D., Robinson, M. J. T. (1964). Tetrahedron, 20, 777.
[17] Allinger, N.L., Blatter, H.M. (1961). J. Am. Chem. Soc., 83, 994.
[18] Abraham, R. J., Chadwick, D. J., Griffiths, L., Sancassan, F. (1980). J. Am. Chem. Soc., 102, 5128.
[19] Servis, K. L., Bowler, D. J., Ishii, C. (1975). J. Am. Chem. Soc., 97, 73. [20] Baker, J. W. (1934). Tautomerism, 179.
[21] Beeslev, R. M., Ingold, C. K., Thorpe, J. F. (1915). J. Chem. Soc., 107, 1080.
[22] Potts, A. R., Baer, T. (1997). J. Phys. Chem. A, 101, 8970.
[23] Allinger, N., Freiberg, L. A. (1962). J. Am. Chem. Soc., 84, 2201.
[24] Potts, A. R., Baer, T. (1998). J. Chem. Phys., 108, 869.