Diseño de una red de intercambio de calor utilizando la metodología supertargeting del punto de pliegue

RESUMEN

La integración de procesos es un campo en crecimiento en la ingeniería de procesos. El análisis de punto de pliegue es una metodología para el diseño de sistemas de intercambio de calor más eficientes que llevan a un mejor diseño del proceso a través de consideraciones sistemáticas para el mejor consumo de la energía, en la inversión de capital y en la reducción de emisiones. La tecnología ha evolucionado para obtener los costos de capital previos al diseño, la cual recibe el nombre de SUPERTARGETING. El objetivo del trabajo es diseñar una red de intercambio de calor de un proceso utilizando la metodología SUPERTARGETING. Para poder seleccionar una red de intercambio de calor se requieren diferentes criterios, los cuales son especificados por las necesidades del diseño y por la flexibilidad de cada diseño. Se analizan diferentes criterios de selección y se propone uno. El uso de la metodología de punto de pliegue da un acercamiento al desarrollo de redes de intercambio de calor óptimas. La metodología es muy efectiva dado que permite utilizar en su valor mínimo los servicios auxiliares manteniendo un área mínima de intercambio de calor. Conjuntamente, proporciona una gran variedad de redes de intercambio de calor y una gran flexibilidad en el diseño de las redes, con lo que da la posibilidad de poder escoger de los diferentes diseños cuál es el óptimo para la planta que se está armando.

Palabras clave: Pinch, Tecnología, Supertargeting, Intercambiadores de calor, redes.

ABSTRACT

Process integration is a growth field in Process Engineering. The Pinch Technology is a methodology to design heat exchanger networks in a more efficient way leading to a better process design through systematic considerations for better energy consumption, for capital investment, and in reducing emissions. Technology has evolved to obtain capital costs previous to the design; its name is SUPERTARGETING. The aim of this work is to design a process heat exchanger network using SUPERTARGETING methodology. In order to select a heat exchanger network several criteria are required, which are specified by the needs of design and by the flexibility of each design. Diverse selection criteria are analyzed and one is proposed. The use of the Pinch Technology provides an approach to optimal heat exchangers networks development. Methodology is rather effective as it allows using in its minimum value the auxiliary services keeping a minimum area of heat exchange. It also provides a great variety of heat exchange networks and a great flexibility in designing networks, generating the possibility of choosing out of the various designs, which one is the optimum for the plant being assembled.

Key words: Pinch, Technology, Supertargeting, Heat exchangers, Network.

INTRODUCCIÓN

El elevado crecimiento de la economía en los últimos años se traduce en una extraordinaria expansión del consumo de energía, por lo que la eficiencia energética se ha convertido en un tema importante en el sector industrial. Los costos energéticos representan una proporción elevada en los presupuestos globales de producción en distintos sectores industriales. Al mismo tiempo, éstos enfrentan una severa competitividad en el mercado y en las regulaciones ambientales.

Bajo estas premisas la mayoría de las compañías se centran en incrementar el uso eficiente de energía que, junto con la diversificación energética, es la principal herramienta para disminuir el consumo de energía en el mundo.

El incremento en los precios de la energía, las limitaciones de capital, los recursos humanos y la incertidumbre del suministro de energía, han hecho que los estudios integrales de energía sean una estrategia de gran importancia para la división industrial.

La integración de procesos es un campo en crecimiento en la ingeniería de procesos. Este término fue desarrollado hace más de veinte años por distintas universidades como UMIST, ICI, ETH Zurch, Leeds University, entre otras y representa opciones para optimizar energéticamente las operaciones unitarias del proceso, así como la interacción de estas unidades, maximizando la eficiencia energética del proceso. En todos estos años se han podido identificar una gran variedad de objetivos cuando se utilizan como:

• Minimizar el costo total anual identificando el punto óptimo entre los costos de operación y los de inversión.

• Incrementar la producción a través de esta forma para quitar los cuellos de botella de la planta.

• Minimizar emisiones indeseables del proceso.

Ante esto, el análisis de punto de pliegue es una metodología para el diseño de sistemas de intercambio de calor más eficientes que llevan a un mejor diseño del proceso a través de consideraciones sistemáticas para el mejor consumo de la energía, en la inversión de capital y en la reducción de emisiones. Esta tecnología demuestra que es posible el establecimiento de diseños de intercambio térmico con un número mínimo tanto de unidades de intercambio de calor como de área de transferencia de calor maximizando la recuperación de calor y distribuyendo de forma óptima el uso de los servicios auxiliares.

Linnhoff [1] y Robin Smith [2] presentan una metodología que es un acercamiento gráfico que permite entender cómo se comporta el proceso termodinámico y cómo se utilizan las leyes de la termodinámica para alcanzar el diseño óptimo de la red de intercambio de calor. Esta metodología se basa en identificar metas en el uso de la energía de un proceso [3] e identificar el punto de pliegue [4]. Este punto es un nivel de temperatura en el que el proceso presenta un cuello de botella para la recuperación de energía. El procedimiento predice el funcionamiento óptimo de ésta, considerando los costos de capital y de energía, haciéndose previo al diseño. Después, se desarrolla el esquema alcanzando la meta [5]. Finalmente, se optimiza tanto para los costos de capital como para los de energía.

La tecnología ha evolucionado para obtener los costos de capital previos al diseño [6]. Por lo que, esta nueva metodología termodinámica ha surgido para alcanzar los mínimos en el uso de la energía y en los de capital previos al diseño [7], la cual recibe el nombre de SUPERTARGETING.

Así, el objetivo del trabajo es diseñar una red de intercambio de calor de un proceso utilizando la metodología SUPERTARGETING de punto de pliegue y para efectuar el diseño se utilizará el software desarrollado por la compañía Linnhoff & March llamado SUPERTARGET.

METODOLOGÍA

Conceptos básicos y características de la metodología de punto de pliegue.

El diseño de procesos inicia con el sistema de reacción. Una vez determinados los flujos de alimentación y del producto y la recirculación de las corrientes, se diseñan los separadores. Posteriormente, se continúa con el diseño del sistema de intercambio de calor. Los servicios auxiliares se utilizarán para satisfacer el calentamiento y enfriamiento que no se pudo satisfacer con la red de intercambio de calor entre corrientes de proceso.

El papel de los principios termodinámicos en la tecnología de punto de pliegue (pinch).

En general, la tecnología de punto de pliegue se basa en el diseño de redes de intercambio de calor (HEN, por sus siglas en inglés) y en los servicios auxiliares. El concepto clave para realizar el análisis se presenta en la construcción de curvas compuestas que son diagramas de temperatura (T) contra entalpía (H). Éstas se usan para realizar metas energéticas precediendo al diseño o al rediseño del proceso y predice la localización del punto de pliegue [1].

Antes de llevar a cabo cualquier diseño, esta técnica se enfoca en obtener metas prácticas como incrementar el funcionamiento energético del sistema y alcanzar un número óptimo en los equipos que conformen la red de unidades de transferencia de calor (o intercambiadores) [1]. Para mucha gente, la termodinámica está asociada con costos energéticos y sus argumentos sólo son prácticos si el costo de capital es bajo [1].

Hay dos efectos termodinámicos básicos que influyen en el costo de capital. El primero es la fuerza impulsora en el diseño del intercambiador de calor que se refleja en el gradiente de temperatura para la transferencia de calor [8] y el otro efecto es el de la carga total de energía (servicios auxiliares).

Cuando los diseños son estrechos se reduce la diferencia de temperatura, por lo que se necesitan menos servicios y disminución en la carga de energía del proceso, pero el costo de capital se incrementa. Sin embargo, cuando decrece la diferencia de temperatura, la carga de energía mengua.

Estas opciones apuntan hacia posibles ahorros de energía, de capital o diferentes alternativas de integración (diferentes opciones de redes de intercambio de calor).

La técnica de punto de pliegue permite estudiar puntos óptimos entre la recuperación de energía contra el área total de intercambio de calor. El número de unidades individuales de intercambio de calor (enfriadores, calentadores, intercambiadores) necesarios para satisfacer los requerimientos energéticos del proceso son más importantes que el de reducir la recuperación de calor [1], independientemente del área total de intercambio.

Metas energéticas.

La tecnología de punto de pliegue se caracteriza por proporcionar metas energéticas previas al diseño de las redes de intercambio de calor [1].

Curvas compuestas.

El calor que se intercambió entre varias corrientes de proceso ya sean calientes o frías se analiza de la misma manera que se analiza el intercambio de calor entre dos corrientes. Cuando se efectúa entre varias corrientes se realiza una curva compuesta de las calientes y una de las frías las cuales se grafican en un diagrama Temperatura vs. Entalpía (T/H).

La naturaleza de éstas muestra que la diferencia mínima de temperatura puede ocurrir en cualquier punto de la zona de intercambio de calor entre ellas. Para un valor mínimo de ΔTmin, la cantidad de servicios que se muestran son los requeridos para satisfacer el proceso y es el valor del punto de pliegue del proceso [1]. Esto quiere decir que es posible diseñar una red de intercambio de calor que utilice sólo el mínimo de los servicios auxiliares indispensables en este punto el intercambiado de calor y opere a valores de ΔT inferiores a ΔTmin.

La curva compuesta Grand. [1]

La curva compuesta Grand (GCC, por sus siglas en inglés) es una representación gráfica de la cascada de energía del proceso. Ayuda a entender las fuentes de energía y los sumideros de energía del proceso. El punto de pliegue divide en 2 regiones características al proceso: el sumidero de energía localizado arriba y la fuente de energía en la parte inferior del mismo [1].

Al mismo tiempo, es una herramienta del análisis del punto de pliegue que proporciona los requerimientos de los servicios auxiliares.

Algoritmo de la Tabla Problema.

El algoritmo de la tabla problema es un procedimiento donde no es necesario realizar gráficas y se lleva a cabo en tres pasos:

1. Convertir las temperaturas del proceso en intervalos incrementando o disminuyendo por ΔTmin el valor de la corriente, según sea fría o caliente, respectivamente.

2. Realizar el balance de energía de las corrientes que forman los intervalos de temperatura.

3. Proporcionar el flujo de calor del servicio auxiliar de calentamiento sobre la base del valor más negativo de la cascada producida.

Con este ajuste de la cascada se puede identificar que uno de los intervalos tiene valor cero (punto de pliegue). Y se muestran dos temperaturas de pliegue (caliente y fría) ya que el valor de la tabla anterior es un intervalo.

Los valores que salen y entran en esta misma columna (cascada corregida) son las cantidades necesarias de calentamiento y enfriamiento del problema para el valor de ΔTmin que se usó.

Costos energéticos del proceso.

Una vez que se escogió la ΔTmin y que los requerimientos energéticos del proceso son evaluados por las curvas compuestas, se procede a obtener los costos energéticos para los niveles de servicios auxiliares requeridos por el proceso.

Metas de Capital.

Obtención del área mínima de la red de intercambio de calor.

La tecnología de punto de pliegue permite crear una meta que sirva para comparar qué tan ideal es el diseño de la red de intercambio de calor. Ésta es el área mínima de la red de intercambio de calor.

Ésta se obtiene de las curvas compuestas balanceadas, las cuales se dividen en regiones verticales llamadas intervalos de entalpía. Con ello, el balance de energía, se puede encontrar el valor del cambio de entalpía del intervalo y las temperaturas que conforman el intervalo y emplear la ecuación de diseño de las unidades de intercambio de calor para obtener el área mínima suponiendo que es una unidad de intercambio totalmente vertical (intercambiadores a contracorriente) y considerando coeficientes de película individuales independientes de los tipos de fluidos que interactúan.

Número mínimo de unidades de transferencia de calor.

Para obtener el número mínimo de unidades de transferencia de calor (Umin) requeridas para la recuperación máxima de energía, la red de intercambio de calor se evalúa previa al diseño de la red utilizando una simplificación del teorema general de redes de Euler, el cual se aplica al diseño de la red de intercambio de calor por medio de la siguiente fórmula:

Donde:

Umin = N – 1 (eq. 1)

Umin = Número mínimo de unidades de intercambio de calor.

N = Número de corrientes de proceso junto con las corrientes de los servicios auxiliares.

Un acercamiento real del número mínimo de unidades de transferencia de calor para alcanzar la máxima recuperación de calor (UminMER) en la red de intercambio de calor es la suma de las unidades obtenidas por este teorema, evaluando por separado las regiones de arriba y de abajo del punto de pliegue.

Costos de capital.

Costo de la red de intercambio de calor.

Cuando se obtiene el área de la red de intercambio de calor y las unidades de transferencia de calor, se puede estimar el costo de la red de intercambio de calor a través de la siguiente fórmula [7]:

(eq. 3)

En este trabajo se utilizarán los siguientes valores de las constantes:

Tabla 1. Constantes de la ecuación de costo de un intercambiador de calor.

Estimación del valor óptimo de ΔTmin.

En este punto recae la importancia de utilizar la metodología de SUPERTARGETING y por medio de la optimización de ΔTmin se puede encontrar el costo total mínimo de la red de intercambio de calor.

Cuando la diferencia de temperaturas mínima disminuye, el área de la red de intercambio de calor aumenta, disminuyendo el costo de la energía (servicios). Y si la diferencia de temperaturas mínima aumenta, los costos de la energía aumentan y los del área disminuyen.

La diferencia mínima de temperaturas óptima se obtiene con el costo mínimo total de la red de intercambio de calor.

Desarrollo de la red de intercambio de calor óptima.

Diseñando para alcanzar la máxima recuperación energética del proceso.

Por arriba del punto de pliegue las corrientes calientes son enfriadas desde la temperatura suministrada hasta la temperatura donde se presenta el punto de pliegue, y las frías calentadas desde la del punto de pliegue hasta la final. Por debajo del punto de pliegue la posición es invertida con las corrientes calientes, enfriadas desde la temperatura del punto hasta la requerida por el proceso y las corrientes frías son calentadas desde la suministrada hasta la del punto de pliegue.

El diseño se ejecuta por medio de los siguientes puntos:

· Dividir el problema en el punto de pliegue.

· Diseñar por separado las dos regiones.

· Empezar el diseño en el punto de pliegue.

· Seguir las desigualdades de los CPs.

· Maximizar las cargas de calor de las unidades de intercambio.

· Sólo poner servicios de calentamiento por arriba del punto de pliegue, y de enfriamiento por debajo del punto de pliegue.

El método que se usa en este punto para diseñar la red de intercambio de calor [5] lleva a encontrar las redes de intercambio de calor que satisfagan las metas de energía, pero no se cumplen las de área. Para aproximarse al valor óptimo dentro del 10% de las metas se propuso una extensión al método de punto de pliegue [9]. Esto se hace utilizando el número mínimo (o cerca del mínimo) de unidades de intercambio de calor y manteniendo los requerimientos de servicios auxiliares del proceso. En la práctica no se diseña queriendo alcanzar un intercambio de calor vertical porque esto llevaría a un diseño demasiado complejo para llevarlo a la práctica (muchas unidades de intercambio de calor y muchas divisiones de corrientes). No obstante, se tratará de alcanzar un diseño de red de intercambio de calor lo más vertical posible con el número mínimo de unidades de intercambio y de divisiones de corrientes.

En otras palabras, se sacrificará una pequeña cantidad del área para alcanzar una mayor simplificación en la estructura de la red manteniendo las metas energéticas que se alcanzaron en el proceso. Para lo anterior es necesario utilizar la metodología de punto de pliegue junto con las técnicas que utiliza SUPERTARGET e ir sondeando el diseño hasta hallar el óptimo. Esto puede llevar a más de dos corridas, por lo que se irá detallando cómo se pueden comparar los diseños con las metas descritas anteriormente.

Las dos técnicas propuestas por el software son:

· Desarrollar la gráfica de fuerzas impulsoras de las unidades de intercambio propuestas en la red de intercambio y

· Explicar un análisis cuantitativo para identificar si el intercambiador propuesto es factible en términos de costo de capital.

Gráfica de la fuerza impulsora de las unidades de intercambio de calor.

El área mínima que se alcanzó por medio de las curvas compuestas está basada en diferencias de temperaturas verticales. Idealmente se necesita cuantificar éstas de las unidades de intercambio propuestas en el diseño de la red de intercambio contra las fuerzas impulsoras disponibles en las curvas compuestas del proceso. Un método simple para realizar el objetivo anterior es representar la diferencia de temperatura vertical entre las curvas compuestas y analizar el cambio que presenta este valor con respecto a la curva compuesta fría (Tfría), por ejemplo. Esta línea se considera la línea “ideal” de DT, es decir, a la que se debieran aproximar los cambiadores de calor.

Después se grafican las unidades de intercambio propuestas en la red de intercambio de calor. Lo que se busca con esta comparación es utilizar correctamente las fuerzas impulsoras de las unidades de intercambio de la red, como lo de la figura 1, que se explica a continuación:

Para alcanzar el valor del área mínima propuesta por el método es necesario que cada intercambiador en la red alcance la diferencia de temperatura que se muestra en la figura 1(a).

El intercambiador propuesto de la figura 1(b) se acerca mucho a la línea “ideal” de ∆T de la gráfica por lo que es una propuesta de intercambio que tiene un buen uso de las fuerzas impulsoras. Mientras que el propuesto en la gráfica 1(c) no se acerca a la línea “ideal” de ∆T y hace un mal uso de las fuerzas impulsoras.

Figura 1. Obtención de la gráfica de fuerzas impulsoras.

Análisis cuantitativo del problema.

El análisis que hace la gráfica de las fuerzas impulsoras sólo analiza la diferencia de temperatura sin considerar el efecto de la carga térmica en el área de intercambio. Con lo que se necesita una valoración cuantitativa de la gráfica de las fuerzas impulsoras, mediante una mejor aproximación al área mínima.

Cuando se diseña la red y se propone un intercambiador, es importante cuantificar si el propuesto traerá un incremento en el uso de los servicios (se hará una penalidad) sin terminar el diseño de la red. Este análisis se realiza proponiendo un intercambiador y analizando otra vez la red (obtener los requerimientos mínimos de la “nueva red”) solamente con lo que queda. Haciendo esto, dos resultados pueden ocurrir al obtener otra vez todos los requerimientos:

1. La cantidad necesaria de servicios auxiliares para satisfacer el proceso no cambia. En este caso, el usuario conoce que el intercambiador propuesto no trae una penalización que significa incrementar el uso de los servicios auxiliares.

2. Se incrementa el uso de servicios auxiliares. En este caso, el intercambiador está transfiriendo calor a través del punto de pliegue o puede traer otra propuesta que cambie calor a través de este punto y se siga el diseño. Si la propuesta no transfiere calor, entonces el incremento en los servicios recae en que el intercambiador es demasiado grande respecto al que se propuso.

El uso más importante del análisis cuantitativo es alcanzar la meta de área mínima.

Después de realizar el análisis anterior, se puede hacer una comparación entre las diferentes redes de intercambio de calor obtenidas, a lo que llamamos “análisis de Unidades Auxiliares (UA)”.

El análisis de UA es una comparación de los valores de UA entre las diferentes redes de intercambio, el cual muestra los posibles cambios que se pueden llevar a cabo en el área total de la red de intercambio de calor.

Optimización de la red de intercambio de calor.

La metodología utiliza dos herramientas para poder alcanzar un valor de UA cercano al ideal, las cuales son:

· Encontrar los ciclos y las trayectorias de la red de intercambio.

· Proponer un valor de la diferencia mínima en un intercambiador (EMAT, por sus siglas en inglés).

La ventaja de utilizar estas dos herramientas es la de simplificar el diseño, obteniendo una red con un número mínimo de unidades de intercambio y mantener el uso de servicios auxiliares al mínimo posible.

Ciclos y caminos en la red de intercambio de calor.

Como se mencionó anteriormente, la metodología de punto de pliegue se enfoca en diseñar la red de intercambio de calor que consuma la mínima cantidad de energía mientras se mantenga el número de unidades de intercambio de calor en su mínimo. La gráfica de fuerzas impulsoras y el análisis cuantitativo ayudan al usuario a minimizar el área de la red, pero el costo total no está en su valor mínimo y se requiere de una optimización final.

Los grados de libertad disponibles para realizar la optimización son los siguientes:

• Mientras que la red inicial se obtiene respetando la descomposición del punto de pliegue y el no violar la diferencia mínima de temperaturas, se encontrarán más unidades de intercambio que las mínimas propuestas. Esto quiere decir que existen ciclos en la red, donde se pueden encontrar más de dos unidades de intercambio y teniendo capacidades de transferencia de calor que pueden ser modificadas de modo sistemático sin cambiar las temperaturas de las corrientes. Estos ciclos pueden ser empleados para quitar unidades de intercambio pequeños o simplemente para distribuir el área de la red bajando el costo total anual del proceso.

• El otro son las trayectorias que se pueden encontrar en la red y se definen como la ubicación de dos servicios auxiliares (caliente y frío) que se conectan con un intercambiador de calor del proceso. Se utilizan para restaurar las fuerzas impulsoras que fueron afectadas por utilizar los ciclos, los cuales al quitar un intercambiador cambian su capacidad y sus temperaturas. Ayudando a restablecer el ΔTmin, ubicar mejor el área y la capacidad de transferencia de calor del intercambiador. Sin embargo, hay un incremento en el consumo de servicios auxiliares.

La segunda herramienta propuesta por la metodología es: utilizar una diferencia mínima en un intercambiador (EMAT). Ésta permite proponer un EMAT para un intercambiador permitiendo que existan entrecruzamientos de temperaturas en el diseño de la red de intercambio de calor. Su uso crea nuevos diseños para mantener un número de unidades de intercambio bajo y evita que existan divisiones en las corrientes. También se puede utilizar con los ciclos.

El SUPERTARGET utiliza el EMAT para simplificar la red de intercambio de calor y proporciona el valor de UA para cada red que se diseña y comparando el diseño que se realiza con el “ideal”. Este valor da una idea de qué tan eficiente es el diseño en términos del costo de capital manteniendo el del energético constante.

RESULTADOS

Aplicación de la metodología de punto de pliegue a un caso simple de cuatro corrientes.

En la figura 2 se presenta un diagrama de flujo simplificado del proceso.

Figura 2. Diagrama de flujo del caso base para aplicar la metodología.

Las corrientes que se considerarán para la aplicación de la metodología son las que se presentan en la tabla 2 y los servicios de calentamiento y enfriamiento en la tabla 3.

Tabla 2. Corrientes de proceso y de servicios del caso base.

Tabla 3. Corrientes de proceso y de servicios del caso base

Selección del valor de ΔTmin inicial.

En la tabla 4 se presentan valores recomendados de ΔTmin para diferentes sectores industriales. Para este proceso se utilizará una ΔTmin inicial de 20°C.

Tabla 4. Valores de ΔTmin recomendados [1]

Curvas compuestas.

Con la información anterior, se obtienen las curvas compuestas caliente y fría del proceso. En la figura 3 se presenta la gráfica de las curvas compuestas del caso base y en la figura 4, la de Grand.

Figura 4. Curva compuesta Grand

Costos energéticos.

Se manejarán 1000 KW de vapor de alta presión con un costo de 71.10 dólares por KW al año y se emplearán 800 KW de agua de enfriamiento con un costo de 6.7 dólares por KW al año.

Número mínimo de unidades de intercambio de calor.

Usando la ecuación de Hohmann, se determina el número mínimo de unidades de transferencia de calor para cada sección del punto de pliegue.

Arriba del punto de pliegue: NUTmin = (5 -1) = 4 Abajo del punto de pliegue: NUTmin = (4 -1) = 4 Por lo tanto: NUTminRed = 4 + 3 = 7

Obtención del área mínima de la red de intercambio de calor.

Mediante la propuesta del arreglo vertical, se obtiene el valor del área mínima y el de UA de toda la red, que servirá de comparación cuando se realice el diseño de la red de intercambio de calor (véase tabla 5).

Tabla 5. Áreas mínimas arriba y abajo del punto de pliegue y valor de UA del caso base.

Costos de capital.

Utilizando la ecuación (2), se tiene que el costo de capital de la red, el cual es de 255,875 USD/año.

Optimización del valor de ∆Tmin.

Para calcular este valor es necesario obtener, para varios valores de ∆Tmin, el de costo total de la red de intercambio de calor. El óptimo de ∆Tmin es el que tenga los costos mínimos. La siguiente gráfica presenta la curva de optimización de ∆Tmin.

Figura 5. Curva de optimización de ΔTmin

El valor óptimo de ΔTmin es 26°C. En este punto se presenta un área mínima de 537.86m2. Los requerimientos de servicios auxiliares de calentamiento son 1,240KW y para los servicios de enfriamiento 1,040KW dando un costo de 95,132 USD/año, y para los de capital, aunque se necesitan las mismas unidades de intercambio, disminuye a 233,184.9 USD/año.

Diseño de la red de intercambio de calor óptima.

En esta sección se diseñarán tres redes de intercambio de calor. El objetivo es demostrar qué red de intercambio de calor da los mejores resultados tanto para el costo de capital como para el energético.

Las redes de intercambio de calor que se presentarán serán las siguientes:

•Primer caso, con el valor inicial de ∆Tmin y UA menor.

•Segundo caso, con el valor óptimo de ∆Tmin y UA menor.

•Tercer caso, con el valor óptimo de ∆Tmin y unidades de transferencia mínimas.

Para cada red se dará tanto el costo de capital como el de servicios y su distribución de áreas para escoger cuál es mejor.

La primera red de intercambio presenta el valor más pequeño de UA. La figura 6 es la representación de las unidades de intercambio y la figura 7 presenta la gráfica de las fuerzas impulsoras. Para el análisis cuantitativo, SUPERTARGET hace un arreglo que mantiene el uso de los servicios auxiliares requeridos y permite una violación del punto de pliegue para optimizar la red de intercambio de calor, por lo que el análisis cuantitativo está ligado al valor de UA de la red de intercambio.

Figura 6. Red de intercambio de calor de la primera propuesta.

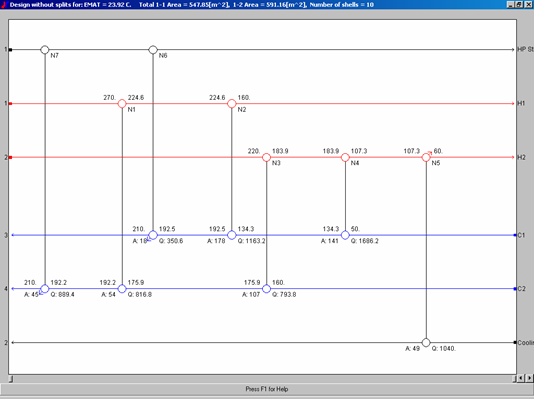
Figura 7. Fuerzas impulsoras de la primera propuesta.

En la gráfica anterior se puede ver que la red presenta un buen comportamiento con lo que respecta a las fuerzas impulsoras. El costo de esta red se presenta en la Tabla 6:

Tabla 6. Valores de la primera opción

La segunda y la tercera opción se analizan de la misma manera. Las figuras 8 y 9 presentan la red de intercambio de calor y la gráfica de fuerzas impulsoras de la segunda opción, respectivamente, mientras que las figuras 10 y 11, la red de intercambio de calor y la gráfica de las fuerzas impulsoras de la tercera opción.

Figura 8. Red de intercambio de calor de la segunda opción.

Figura 9. Fuerzas impulsoras de la segunda opción.

Figura 10. Red de intercambio de calor de la tercera opción.

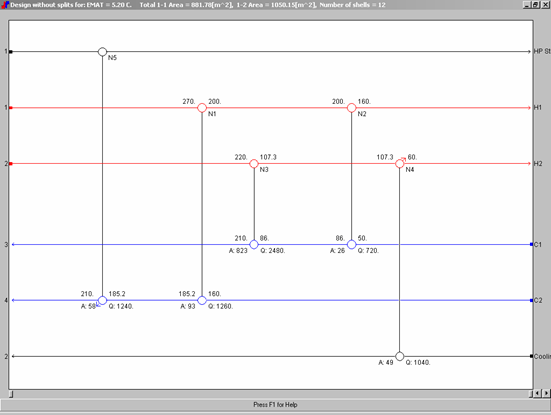
Figura 11. Fuerzas impulsoras de la tercera opción.

En la figura 9 se observa que la segunda opción hace buen uso de las fuerzas impulsoras, mientras que para la tercera opción (fig. 11), las unidades de transferencia HX2 y HX3 hacen mal uso de las fuerzas impulsoras, originando un exceso de área de esta red.

En la tabla 7 se presentan los resultados para las tres opciones analizadas:

Tabla 7. Valores de costos, UA y número de cambiadores de las opciones analizadas.

ANÁLISIS DE RESULTADOS

Selección de la red de intercambio de calor optima.

Para poder seleccionar una red de intercambio de calor se requieren diferentes criterios, los cuales son especificados por las necesidades del diseño y por la flexibilidad de cada diseño.

En esta sección se analizarán diferentes criterios de selección. Se hará una breve explicación de los criterios y se propondrá uno más.

Opción propuesta por Bodo Linnhoff [1] y Robin Smith. [2]

El método propuesto por estos investigadores se basa en la selección de dos tipos diferentes de intercambiadores. El primer tipo es un intercambiador a contracorriente de coraza y tubos, el cual presenta una coraza y un paso en los tubos (intercambiador del tipo 1-1). Los investigadores descubrieron que este tipo de cambiador presenta poca área pero es más complicado el mantenimiento y la eficiencia; mientras que con el segundo tipo que es una coraza y dos pasos de tubos, sólo se necesita mayor área de intercambio pero presenta ventajas prácticas cuando se consideran (mantenimiento y eficiencia).

Los intercambiadores 1-2 (una coraza y dos pasos por los tubos) muestra un flujo a contracorriente y uno a corriente, por lo que la eficiencia en las fuerzas impulsoras se reduce a comparación al intercambiador 1-1. Por eso se introduce un factor de corrección (Ft), que se obtiene a partir de dos valores que se relacionan con las temperaturas de entrada y de salida del intercambiador. Cuando se utiliza este factor se encuentran tres posibilidades:

i. Existe una aproximación: la temperatura inicial de la corriente caliente es mayor que la final de la corriente fría.

ii. La aproximación es cero: la temperatura inicial de la corriente caliente es igual a la de salida de la corriente fría.

iii. Hay un cruzamiento en las temperaturas: la temperatura de salida de la corriente fría es mayor a la inicial de la corriente caliente.

Para cada caso se dará un valor de Ft y el valor mínimo permitido es de 0.8, que es lo aceptable para un cruzamiento de temperaturas. Valores de Ft menores al propuesto caen en una zona en la que no es posible el intercambiador. Aquí, se requiere diseñar un intercambiador donde existan más pasos por los tubos y más corazas.

Esta opción considera que la mejor red será la que contenga un número mínimo de unidades de intercambio de calor.

Opción propuesta por Badr Abdullah Al-Riyami y Jiri Klemes [10], del departamento de integración de procesos de la Universidad de Manchester.

Esta opción considera dos tamaños diferentes de intercambiadores, obteniendo el número de corazas y la relación del área total de la red de intercambio de calor. Se asignan a los cambiadores 1-1 con la coraza del mismo tamaño. Asimismo, se toma en cuenta la red óptima que es la que tenga menos área total, y el arreglo de los cambiadores de dos tamaños cada uno con el tamaño de coraza promedio. Una consideración importante es que el arreglo debe de respetar el uso mínimo de servicios auxiliares que se tomó al principio.

Opción que se propone en este trabajo.

Se basa principalmente en el aspecto práctico del diseño de la red de intercambio de calor. Cuando se analiza la red de intercambio de calor se denota que las unidades de transferencia de calor diseñadas presentan una distribución de áreas. Al estudiarlo se vio que cada unidad contiene una cantidad determinada de intercambiadores de calor. Este trabajo propone que la red que tenga una distribución de áreas más estable en las unidades de intercambio de calor, será la más sencilla de colocar y la que no contenga gastos extras por diseño de materiales especiales para satisfacer la que se propuso en SUPERTARGET.

Este análisis se fundamenta en que cuando queremos diseñar sólo podemos encontrar intercambiadores existentes (áreas estándar) y los accesorios para éstos. Por lo que mandar a hacerlos especiales traería un costo adicional en los accesorios y en el mantenimiento para cada uno.

Así, la propuesta presente simplifica el diseño de la red después de los resultados que nos proporciona el SUPERTARGET, ya que mantiene los costos de servicios auxiliares al mínimo con el área lo más estable posible (prácticamente realizable). Por lo que esta opción se derivó de las dos anteriores. De la opción de Bodo Linnhoff [1] se toma cómo se colocarían las unidades de transferencia de calor (serie o paralelo) por medio del valor de Ft y de la segunda se consideró el uso de los 2 intercambiadores estándar para hacer el diseño de la red.

Aplicación de las opciones. Opción de este trabajo.

Se puede ver que por medio de las gráficas de las fuerzas impulsoras la distribución de áreas que se propone es mejor para la primera y la segunda opción. Si en estos dos casos se toma la unidad de intercambio de calor más pequeña y se le asigna a un tamaño de cambiador se puede demostrar que es más factible para ambas. Ahora el criterio de selección se convierte en que la segunda es más barata, porque la efectividad de la metodología encontró el uso mínimo de servicios auxiliares para el valor óptimo de ΔTmin.

Opción de Bodo Linhoff [1] y Robin Smith. [2]

Para ésta se debe hacer un análisis de la red que presenta el número mínimo de unidades que son la segunda y la tercera propuesta. La siguiente tabla da el análisis de las redes y la distribución de los cambiadores en la red:

Tabla 8. Consideraciones para escoger la red por medio de Linnhoff [1] y Smith [2].

La segunda red de intercambio de calor nos muestra más unidades de intercambio de calor pero menos corazas. Al analizar las áreas si queremos que nuestra red de intercambio sea práctica debemos utilizar las intercambiadores 1-2, por lo que se escogió la segunda que nos da un número menor de corazas y el área de los intercambiadores 1- 1 y el área de los intercambiadores 1-2 son muy parecidas y los valores de Ft cercanos a uno. Esto quiere decir que el área es menor y se ajusta a un diseño práctico. Con lo que, el mejor arreglo es la segunda opción.

Opción de la Universidad de Manchester. [10]

Para ésta la consideración del área mínima es para la segunda red de intercambio de calor, tomando un tamaño de coraza promedio para las unidades de intercambio. Las áreas de cada red, se muestran en la Tabla 9:

Tabla 9. Representación de la opción de la Universidad de Manchester.

Esta opción también nos demuestra que la segunda es la mejor red de intercambio de calor.

CONCLUSIONES

El uso de la metodología de punto de pliegue da un acercamiento al desarrollo de redes de intercambio de calor óptimas. La metodología es muy efectiva dado que permite utilizar en su valor mínimo los servicios auxiliares manteniendo un área mínima de intercambio de calor. Conjuntamente, proporciona una gran variedad de redes de intercambio de calor y una gran flexibilidad en el diseño de las redes, con lo que da la posibilidad de poder escoger de los diferentes diseños cuál es el óptimo para la planta que se está armando.

REFERENCIAS

[1] Linnhoff, B. et al. (1982). “A user guide on process integration for efficient use of energy”, Chem. Eng.

[2] Smith Robin. (1995). “Chemical Process Design”, McGraw Hill, Nueva York.

[3] Linnhoff, B and Flower, J. R. (1978). “Synthesis of HEN. Part 1: Systematic generation of energy optimal networks”, AIChE Journal, 24 (4), 642.

[4] Linnhoff, B., Mason, D. R., and Wardle, I. (1979). “Understanding heat exchanger networks”, Comp Chem Eng, 3, 295.

[5] Linnhoff, B. y Hindmarsh, E. (1983). “The pinch design method of heat exchanger networks”, Chem Eng Science, 38 (5).

[6] Townsend y Linnhoff. (1984). “Surface area targets for heat exchangers networks”. I. Chem. E. 11th Annual Res. Meeting, Bath, UK.

[7] Ahmad, S. (1985). “Heat exchanger Networks: Cost tradeoffs in energy and capital”, Ph. D. thesis, University of Manchester Institute of Science and technology, England.

[8] Linnhoff, B. y Vredeveld, D. R. (1984). “Pinch technology has come of age”, Chem Eng Prog, 33-40.

[9] Linnhoff, B. y Ahmad S. (1990). “Cost Optimum Heat Exchanger Networks – I Minimum Energy and Capital using Simple Models for Capital Cost”, Comp. Chem. Eng. 14 (7), 729-750.