E. Vargas-Medina1, Walterio W. Mayol-Cuevas2, J. Figueroa Nazuno3 1UAM-Iztapalapa (México)
E-mail: evm@xanum.uam.mx,
2Department of Computer Science, University of Bristol (UK),
3Centro de Investigación en Computación-IPN (México) E-mail: jfn@cic.ipn.mx
Recibido: Abril 3, 2008. Aceptado: Junio 28, 2008
RESUMEN
En el estudio de los modelos estocásticos de interacción de partículas, han surgido una gran cantidad de procedimientos matemáticos que permiten estudiar la interacción de entidades abstractas, bajo diferentes situaciones de “influencia” o efectos mutuos. Uno de estos modelos es el de votación en una, dos y tres dimensiones.
En este trabajo se presenta un breve resumen de un modelo de partículas en interacción (IPS, por sus siglas en inglés) en varias dimensiones y se presentan los resultados de su simulación computacional para el estudio de retículos de partículas en una, dos y tres dimensiones. Se presentan los resultados obtenidos de la modificación de diversos parámetros y condiciones iniciales del sistema de partículas en interacción, que permiten ilustrar su aplicación en el estudio de procesos de participación social, como es la conducta de votación. Se muestra cómo estas herramientas permiten probar diversas hipótesis de los procesos sociales de votación genuina, los cuales no son posibles de estudiar directamente. Los resultados de la simulación computacional muestran la potencialidad de estos métodos para el estudio de fenómenos complejos y que es posible mostrar algunos factores que pueden determinar los cambios abruptos o críticos (transición de fase).
Palabras clave: sistemas complejos, dinámica social, modelos de votación, sistemas de partículas interactuantes.
ABSTRACT
In the study of stochastic models of particle interaction, there have been a number of mathematical procedures allowing to studying abstract entities interaction, under different situations of "influence" or mutual interaction. One of these is the voting model in one, two, and three dimensions.
This paper presents a brief summary of a model of interacting particles (IPS) in various dimensions and presents the results of their computer simulation to study lattices of particles in one, two, and three dimensions. The results present the modification of various parameters and initial conditions of the interacting particles system, allowing illustrating this application in the study of social participation processes, such as voting performance. Results show how these tools enable to test various scenarios of the social processes of political voting, which are not possible to study directly. The results of computer simulation show, in one side, the potential of these methods to study complex phenomena and, in the other side, that it is possible to find some factors that may determine critical changes (Phase Transitions).
Keywords: complex systems, social dynamics, models of voting, interacting particles systems.
INTRODUCCIÓN
Un sistema es un conjunto de elementos o partes que interaccionan entre sí a fin de alcanzar un objetivo concreto. De aquí se desprenden dos implicancias fundamentales. Primero, que existe una influencia mutua entre sus elementos componentes, es decir, que el cambio experimentado en uno de ellos repercute y afecta inevitablemente al resto. Y segundo, que una serie de elementos reunidos (es decir, un conjunto), que no persigue un propósito común (un objetivo), de ninguna manera constituye un sistema. En síntesis, para que el comportamiento de un sistema esté adecuadamente descrito, es necesario conocer, además de sus elementos, las interacciones o relaciones entre ellos. Pero no sólo eso: también se requiere saber sus estados (los valores instantáneos de todos los elementos) y sus transiciones (los cambios dinámicos de esos estados).
Los sistemas complejos se caracterizan fundamentalmente porque su comportamiento es imprevisible. Sin embargo, complejidad no es sinónimo de complicación: este vocablo hace referencia a algo enmarañado, enredado, de difícil comprensión. En realidad, y por el momento, no existe una definición precisa y absolutamente aceptada de lo que es un sistema complejo, pero pueden darse algunas peculiaridades comunes. En primer término, está compuesto por una gran cantidad de elementos relativamente idénticos. Por ejemplo, el número de células en un organismo, o la cantidad de personas en una sociedad. En segundo lugar, la interacción entre sus elementos es local y origina un comportamiento emergente que no puede explicarse a partir de dichos elementos tomados aisladamente. Un desierto puede contener billones de granos de arena, pero sus interacciones son excesivamente simples comparadas con las que se verifican en las abejas de un enjambre. Por último, es muy difícil predecir su evolución dinámica futura; es decir, lo que ocurrirá más allá de un cierto horizonte temporal.
En la naturaleza se pueden encontrar una gran cantidad de ejemplos de sistemas complejos que se extienden desde la física hasta la neurología, desde la economía hasta la biología molecular, desde la sociología hasta las matemáticas. Por ese motivo, esta clase de sistemas no constituye un caso raro ni excepcional sino que se manifiesta en la inmensa mayoría de los fenómenos que se observan a diario. Sin embargo, y a pesar de su gran diversidad y abundancia, se pueden identificar conductas dinámicas genéricas, no importa su naturaleza (física, química, biológica o social); entre ellas, las leyes de crecimiento, la autoorganización y los procesos colectivos emergentes. Como ejemplos de sistemas complejos se pueden mencionar ―entre otros― una célula, un cerebro, un organismo, una computadora, un ecosistema, una sociedad de insectos, un sistema inmunológico o una economía de mercado.
Estos sistemas complejos manifiestan propiedades denominadas por algunos autores como “emergentes”, es decir, el comportamiento de estos sistemas no depende del comportamiento de cada uno de sus elementos sino de su interacción: se autoorganizan y se adaptan.
Todas esas cuestiones, y otras muchas, son consideradas muy difíciles de estudiar y simular con técnicas clásicas, debido a que estos sistemas o redes (sociales, eléctricas, neuronales, etc.) contenían una gran cantidad de elementos con muchos grados de libertad,1 dándose entre éstos complejas interacciones no-lineales. Aunque se conozca el comportamiento de cada unidad que forma este tipo de sistemas (un individuo, una neurona, un transformador eléctrico, un grupo social, una colectividad, etc.), la suma de los comportamientos de esas unidades no informa sobre el comportamiento de la red o sistema en lo global.
Un aspecto fundamental es que en muchos de estos fenómenos colectivos es extraordinariamente difícil la realización de estudios empíricos; en particular, el probar en forma rigurosa hipótesis explicativas. Desde hace muchos años, en diversas disciplinas científicas se trabaja con modelos matemáticos y/o computacionales; sin embargo, los métodos clásicos para el estudio de los sistemas multivariados, son los sistemas de ecuaciones diferenciales parciales —en algunos casos, con características estocásticas—. Por las razones expuestas ha surgido la necesidad de nuevas formas de estudio de estos fenómenos multivariados. Es en esta perspectiva que surge el paradigma de investigación de los sistemas complejos, siendo uno de estos enfoques el modelo de partículas en interacción.
SISTEMAS DE PARTÍCULAS EN INTERACCIÓN (IPS)
El estudio de los Sistemas de Partículas en Interacción (IPS, por sus siglas en inglés) surgió en la década de los años 60, desarrollándose principalmente como una rama de la Mecánica Estadística aplicada al estudio de los denominados sistemas complejos. [1] Su evolución ha proporcionado nuevas herramientas y puede aplicarse al estudio de diversos campos, como son: redes neuronales, crecimiento de tumores, expansión de enfermedades o infecciones, interacciones conductuales en humanos y, en general, los denominados procesos de difusión. [2-4]
Durrett [5] presenta la definición general de los IPS e introduce diversas clases de estos sistemas. A continuación se presenta el modelo formal de los mismos:
Notación y terminología
1. Consideremos que las partículas interactuantes del sistema están representadas por un conjunto S (ordinariamente finito) de puntos en un retículo (lattice) n-dimensional. Para la mayoría de los autores S = Zd con d≥ 1.
2. Sea F un conjunto finito de valores que simbolizan los estados posibles de cada partícula en cada momento, el cual siempre está en uno de dos estados posibles:
{0,1} o {-1, 1} (presencia-ausencia, ocupado-no ocupado, a favor-en contra).
3. Sea c = Fs el conjunto de todas las funciones desde S hasta F. Si η Є c entonces
η(x) da el estado en x, por lo que η describe la configuración del sistema.
4. Sea L igual al conjunto de todos los subconjuntos de S. Si a Є F, el mapeo η ® {x: η(x) = a} da una correspondencia de 1-1 de L y de x. En algunos ejemplos L es un espacio de estado más conveniente que c.}
Descripción formal
Un IPS es un fuerte proceso de Markov con espacio de estado c o L. Para demostrar resultados interesantes se asume que el proceso se describe mediante una función c:
LXc ® [0,¥] lo cual determina la evolución a través de la ecuación:
P(ηt+d(x) ≠ ηt(x) para todo c Є A | ηt = η)=(∑ c(B,η)) d + 0(d) con d ® 0 [Ec. 1]
BÉA
1 Se entiende como grados de libertad (GDL) de un sistema el número de parámetros independientes que se necesitan para definir unívocamente su comportamiento en cualquier instante.
Es decir, c(A,η) es la tasa a la que cambian los valores en todos los sitios en A cuando la configuración es η. En la mayoría de los modelos que se han estudiado c(A,η)=0 a menos que |A|, la cardinalidad de A, es 1 o 2, y en casi todos estos casos, el proceso es uno de los dos tipos siguientes:
a) sistemas “spin-flip”: c(A,η)=0 a menos que |A|=1. En estos modelos sólo un sitio cambia su estado en un momento, lo que corresponde a: c({x},η) como c(x,η).
b) sistemas de partículas en movimiento (particle motion): F={0,1} y c(A,η)=0 a menos que A={x,y} y η(x)=1, η(y)=0 o que |A|=1. En estos modelos se marca la ubicación de las partículas. En el primer caso una partícula cambia de x a y; en la segunda, aparece o desaparece.
Cada IPS depende de la naturaleza exacta de la interacción y de las herramientas que se utilicen para abordarlo. Cada fenómeno requiere de una formulación matemática específica, tal es el caso de los diferentes modelos generados en esta rama: modelo estocástico de Ising, modelo de votación, procesos de contacto, procesos de exclusión, procesos de difusión o propagación, modelo de autoorganización crítica (self-organized criticaly) etc. [6-12]
Los aspectos más comunes de los IPS son: [13]
1. Como se trata de procesos estocásticos, lo que interesa es observar la evolución de su comportamiento en tiempos relativamente grandes, es decir, lo que ocurre con la sucesión cuando →∞
2. Otro aspecto importante es analizar la ergodicidad del proceso, esto es, si el modelo tiende hacia alguna distribución estacionaria.
3. Es conveniente observar los estados iniciales, es decir, las distribuciones originales de las partículas en la red, para determinar, en la medida de lo posible, qué estados tienden hacia qué configuraciones.
Modelo de Votación
En este modelo cada sitio representa a una persona que puede tener una opinión a favor de uno u otro de varios partidos en disputa, a cada uno de los cuales se asigna un color diferente (estados). El proceso de votación se da por la interacción entre una partícula y sus vecinas más cercanas. En un momento determinado, la persona adopta la opinión o estado de cualquiera de sus vecinas o, contrariamente, puede transmitir la suya. Conforme transcurre el tiempo es posible observar la formación de bloques, de cuya pugna surge finalmente el consenso a favor de uno de ellos. [14,15] Es interesante observar el comportamiento y desarrollo de los bloques o configuraciones en la simulación, poniendo especial énfasis a lo que sucede en los límites de los agrupamientos.
La simulación de este proceso de IPS la realiza Durrett [16,17] en una, dos y tres dimensiones (D), por medio de varios modelos, tres de los cuales se analizan a continuación:
La notación matemática para este modelo en sus tres dimensiones es la siguiente [5:112-113]:
C(x,η)=∑p(y) 1(η(x+y)≠η(x)) [Ec. 2]
yÎS
donde:
c(x,η) es la proporción de cambio de cada una de las partículas x cuando la configuración es ηÎ[0,1] Zd, p(y)≥0 y ∑ p(y)=1
yÎS
Durrett describe el modelo de la siguiente forma: “En el modelo de votación los sitios pueden considerarse como casas de individuos que viven en una gran ciudad idealizada. Los estados 0 y 1 representan la opinión a favor o en contra de una proposición en particular. El individuo en x asigna un peso p(y) a la opinión de la persona en x+y y cambia su opinión con una proporción que es igual a la suma de los pesos de la opinión opuesta”. [5:113].
ESTUDIO EXPERIMENTAL SIMULACIONAL
A continuación se presentan los resultados obtenidos de la simulación por computadora de un caso particular de los IPS: el modelo de votación en una, dos y tres dimensiones. Además, se presentan los resultados en el caso de dos de los modelos en 1-D y en 2-D cambiando las condiciones iniciales (configuración aleatoria vs. no-aleatoria).
Modelo de votación en una dimensión
Este algoritmo simula el modelo de votación unidimensional con 198 sitios. El número de opiniones (estados) que compiten puede ir de 2 a 15, representados por diferentes colores. Consiste en una situación en donde los participantes se encuentran distribuidos en forma tal que cada partícula se comunica y puede ser influida por sus vecinos más cercanos (derecha, izquierda). En este modelo la configuración inicial es aleatoria. Las variables que se pueden manipular al inicio de la simulación son: tiempo de la simulación y número de colores (estados) que interactúan.
El sistema inicia eligiendo una partícula al azar en un momento determinado, ésta adopta al azar el estado (opinión) de uno de sus vecinos cercanos. Este mecanismo conduce al sistema hacia un consenso total y la atención se centra en cómo se forman configuraciones de partículas con la misma opinión y tienden a crecer o a ir cambiando su configuración.
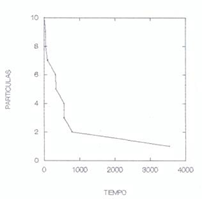
En las gráficas 1 y 2 se muestran las evoluciones de dos ejemplos con este modelo, con 10 y 15 estados respectivamente.

Evolución en tiempo de la cantidad de partículas en interacción para 10 partidos. El eje y representa la cantidad de partículas existentes en cada paso de la evolución.
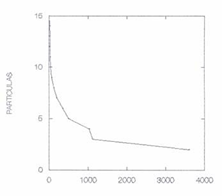
Evolución en tiempo de la cantidad de partículas en interacción para 15 estados diferentes (colores).
Modelo de votación en dos dimensiones
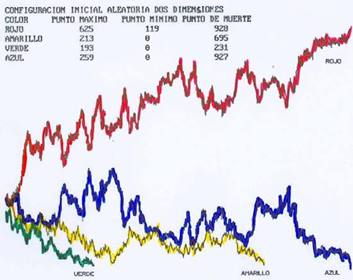
Para simular el modelo en 2D con cuatro estados se construyó el siguiente algoritmo. Tenemos un retículo rectangular de 25x25 sitios (625 participantes), como votantes:
(0, 1, ..., m - × 1) (0, 1, ..., n - 1).
Cada sitio tiene cuatro vecinos; los vecinos de (i, j) son:
(i + 1, j), (i - 1, j), (i, j + 1), y (i, j - 1),
Con esta estructura de vecinos, nuestro conjunto de sitios topológicamente es toroidal (una rosquilla en forma de superficie).
Cada sitio puede estar en cualquiera de 4 diferentes estados, indicados por diferentes colores (azul, verde, rojo o amarillo). Inicialmente, a cada sitio se le asigna al azar uno de los estados posibles (colores). Sin embargo, el sistema puede configurarse para que el estado de un sitio pueda seleccionarse de una lista determinada.
El tiempo de evolución de este sistema es discreto, y la dinámica del proceso de votación en cada tiempo de evolución es como sigue: en cada momento t,
1. Un sitio es elegido al azar (cada sitio tiene la misma probabilidad de ser elegido),
2. Un vecino de este sitio es elegido al azar (cada uno de los 4 vecinos tiene la misma probabilidad de que sea elegido).
3. El estado del sitio seleccionado se cambia al estado del vecino seleccionado.
Para que todos los sitios tengan el mismo color, es decir, para que lleguen a consenso, el lapso de tiempo requerido es del orden de C log n. Se puede observar gráficamente la evolución de la simulación. En cada actualización se lleva un registro del conteo de partículas de cada estado; generalmente, el sistema se detiene cuando todas las partículas llegan a tener un mismo estado.
En las figuras 2 (a-d) se muestra un ejemplo con las configuraciones inicial, dos intermedias y final de una simulación tipo.
a) 
b)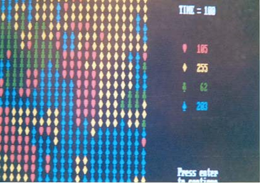
c) 
d)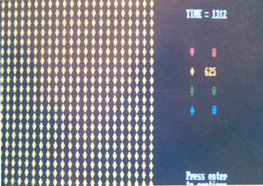
Resultados de la simulación de un proceso de interacción entre cuatro estados (representados por colores y figuras diferentes) en diferentes momentos: inicial (a), intermedios (b, c) y final (d)
Es claro que entre más vecinos del mismo estado se tengan, la probabilidad de lograr el consenso (“ganar”) es mayor. En las gráficas 3 y 4 se muestra el comportamiento de las partículas en diversos tiempos de evolución. En la primera simulación el sistema lleva al consenso en 928 pasos y en la segunda, en 1640 pasos.
Evolución en tiempo de la cantidad de partículas en interacción entre los 4 partidos
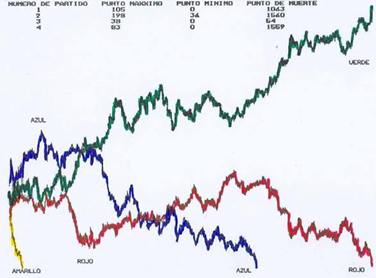
Evolución en tiempo de la cantidad de partículas en interacción entre los 4 partidos
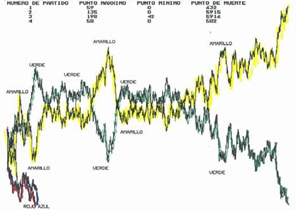
Este algoritmo simula el modelo de votación en 2-D en un cuadrado de 20 x 25 sitios, en el cual a cada sitio se asigna, en forma aleatoria, uno de 2912 estados posibles, es decir, la combinación de 224 caracteres ASCII y 13 colores elegidos al azar (224 x 13 = 2912). El parámetro en el programa original que se puede seleccionar es el tiempo requerido para observar un determinado número de interacciones, o si se desea que el sistema llegue al consenso se puede dejar el programa corriendo hasta que termine (generalmente arriba de 3,000 unidades de tiempo promedio, de acuerdo con los experimentos realizados).
En las figuras 3 (a-e) se muestra un ejemplo con las configuraciones inicial, intermedias y final de una simulación tipo.

Resultados de la simulación de un proceso de interacción entre trece estados (representados por colores diferentes y figuras) en varios momentos: inicial, intermedios y final
Como puede observarse en las secuencias fotográficas, conforme transcurre el tiempo y el sistema evoluciona, las partículas de cada partido se agrupan en bloques que compiten entre sí, de tal manera que se van eliminando hasta que sólo interactúan dos partidos (ver figuras 3c y 3d). En general, se observó que una vez formados los bloques la pugna generalmente se lleva a cabo en los límites. Finalmente, uno de los partidos puede lograr ganar y los 625 sitios quedan ocupados por ese estado (ver figuras 3e y 2d).
Los casos anteriores se refieren a la asignación aleatoria de estados (colores) a sitios en un cuadrado uni y bidimensional. Con el fin de observar el efecto de las interacciones cuando a un estado se le asigna una determinada cantidad de sitios (configuración inicial no-aleatoria), se realizó una modificación al programa con el fin de variar el porcentaje de partículas que interactúan inicialmente de cada estado.
En la tabla 1 se presentan las diferentes configuraciones iniciales que se variaron (Diseño experimental), con la finalidad de encontrar un valor “crítico” a partir del cual un partido o estado determinado tiene la mayor probabilidad de llegar al consenso, de acuerdo con la cantidad de elementos o “adeptos” que inicialmente tiene al empezar a aplicarse la regla de interacción y que el sistema evolucione.
PARTIDOS |
||||
% SITIOS AZULES |
ROJO |
AMARILLO |
VERDE |
AZUL |
25 |
156 |
156 |
156 |
157 |
30 |
145 |
145 |
145 |
190 |
35 |
135 |
135 |
136 |
219 |
40 |
125 |
125 |
125 |
250 |
45 |
114 |
114 |
114 |
243 |
50 |
104 |
104 |
104 |
313 |
55 |
95 |
93 |
93 |
344 |
60 |
83 |
83 |
83 |
376 |
65 |
73 |
72 |
73 |
407 |
70 |
62 |
62 |
63 |
438 |
75 |
52 |
52 |
52 |
469 |
80 |
41 |
41 |
41 |
502 |
85 |
31 |
31 |
31 |
532 |
Diseño experimental para el caso C.
13 configuraciones iniciales para la simulación del modelo.
En la gráfica 5 se muestra el comportamiento tipo de una configuración inicial de partículas distribuidas equitativamente en la red (22% de un partido y el resto en proporciones iguales a los demás). A pesar de tal equilibrio, dos de los partidos se extinguen rápidamente (en los tiempos 582 y 632, respectivamente), mientras que los otros dos partidos interactúan hasta el tiempo 5916.
En las gráficas 6 y 7 se presentan las simulaciones para los casos de porcentajes de 71% y 85% de sitios azules en la configuración inicial.
Evolución en tiempo de la cantidad de partículas en interacción entre los 4 partidos
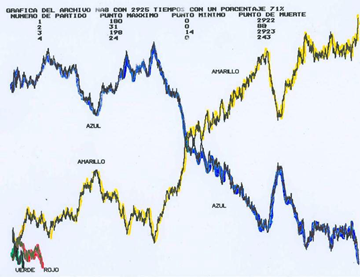
Evolución en tiempo de la cantidad de partículas en interacción entre los 4 partidos
Distribuidos de esta manera, se esperaría que el estado azul lograra el consenso y que los demás se extingan con cierta rapidez, lo cual no sucede. Como se puede observar, uno de los partidos minoritarios en la configuración inicial llega incluso a rebasar el número de partículas del partido mayoritario, e incluso lo supera y gana el consenso (estado amarillo). Esto pudiera deberse a la interacción entre cantidad de partículas y su distribución en el sistema, lo cual permite la aparición de agrupamientos “exitosos” que se difunden en el trascurso de la simulación. Este fenómeno se asemeja a procesos de influencia social denominados “minoritarios”, en donde una “minoría activa” presenta este tipo de manifestación. [18,19]
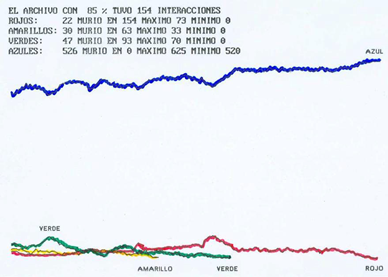
Evolución en tiempo de la cantidad de partículas en interacción
Comparación de resultados en ambas condiciones: configuración inicial aleatoria vs. no- aleatoria
En la tablas 2 y 3 se presentan los resultados de 30 simulaciones diferentes en 1-D y en 2-D respectivamente, con configuraciones iniciales aleatorias, en donde se puede apreciar las diferentes dinámicas de los sistemas.
ESTADOS (PARTIDOS) |
|||||
CORRIDAS |
ROJO |
AMARILLO |
VERDE |
AZUL |
PASOS TOTALES |
1 |
1271 |
***** |
2525 |
426 |
2526 |
2 |
***** |
636 |
2604 |
1469 |
2605 |
3 |
***** |
769 |
2675 |
12728 |
12728 |
4 |
625 |
115 |
2675 |
***** |
2655 |
5 |
***** |
671 |
3645 |
1397 |
3646 |
6 |
***** |
1298 |
66 |
2592 |
2593 |
7 |
***** |
2163 |
501 |
306 |
2164 |
8 |
912 |
30 |
***** |
643 |
913 |
9 |
1386 |
764 |
46 |
***** |
1387 |
10 |
513 |
2612 |
***** |
9701 |
9702 |
11 |
169 |
***** |
690 |
4472 |
4473 |
12 |
6669 |
24 |
***** |
823 |
6670 |
13 |
676 |
4475 |
459 |
***** |
4476 |
14 |
2288 |
195 |
1304 |
***** |
2289 |
15 |
2190 |
11396 |
2388 |
***** |
11397 |
16 |
644 |
1648 |
87 |
***** |
1649 |
17 |
***** |
1367 |
34 |
101 |
1368 |
18 |
784 |
***** |
172 |
292 |
785 |
19 |
460 |
***** |
4181 |
1715 |
4182 |
20 |
***** |
102 |
814 |
8822 |
8823 |
21 |
675 |
1690 |
***** |
5460 |
5461 |
22 |
786 |
1048 |
***** |
256 |
1049 |
23 |
3452 |
361 |
***** |
853 |
3453 |
24 |
652 |
303 |
***** |
5723 |
5724 |
25 |
***** |
738 |
14844 |
308 |
14845 |
26 |
***** |
104 |
10488 |
342 |
10489 |
27 |
7340 |
176 |
***** |
2324 |
7341 |
28 |
452 |
5839 |
***** |
1915 |
5840 |
29 |
467 |
***** |
903 |
6279 |
6280 |
30 |
***** |
2688 |
77 |
1158 |
2689 |
33.33% |
16.66% |
30.00% |
20.00% |
µ= 5006.60 σ = 3772.19 |
|
Nota: ***** = llegó a consenso
Pasos en que cada partido va “desapareciendo” en el sistema, pasos totales necesarios para llegar al consenso y % de veces que cada partido llega al consenso
CORRIDAS |
ROJO |
AMARILLO |
VERDE |
AZUL |
PASOS TOTALES |
1 |
176 |
771 |
481 |
***** |
772 |
2 |
1718 |
991 |
917 |
***** |
1719 |
3 |
348 |
***** |
2079 |
103 |
2080 |
4 |
***** |
152 |
1645 |
600 |
1646 |
5 |
300 |
1362 |
***** |
161 |
1362 |
6 |
***** |
259 |
878 |
752 |
878 |
7 |
924 |
172 |
***** |
1949 |
1950 |
8 |
218 |
1069 |
1286 |
***** |
1287 |
9 |
1120 |
***** |
1023 |
683 |
1121 |
10 |
207 |
***** |
168 |
1946 |
1947 |
11 |
293 |
***** |
609 |
1012 |
1013 |
12 |
2073 |
82 |
657 |
***** |
2074 |
13 |
215 |
***** |
1599 |
115 |
1600 |
14 |
***** |
255 |
499 |
273 |
500 |
15 |
2051 |
***** |
47 |
252 |
2052 |
16 |
192 |
***** |
1209 |
549 |
1210 |
17 |
491 |
106 |
423 |
***** |
424 |
18 |
352 |
1516 |
***** |
565 |
1517 |
19 |
***** |
129 |
414 |
568 |
569 |
20 |
***** |
534 |
1319 |
373 |
1320 |
21 |
144 |
701 |
***** |
559 |
701 |
22 |
***** |
306 |
524 |
1640 |
1641 |
23 |
1641 |
***** |
166 |
1622 |
1642 |
24 |
55 |
***** |
364 |
1111 |
1112 |
25 |
***** |
91 |
512 |
1304 |
1305 |
26 |
198 |
390 |
217 |
***** |
391 |
27 |
502 |
***** |
54 |
192 |
503 |
28 |
***** |
413 |
83 |
2620 |
2621 |
29 |
450 |
***** |
299 |
858 |
859 |
30 |
558 |
171 |
1266 |
***** |
1267 |
25.00% |
38.00% |
13.80% |
23.00% |
µ=1246.74 σ = 598.44 |
Nota: ***** = llegó a consenso
Pasos en que cada partido va “desapareciendo” en el sistema, pasos totales necesarios para llegar al consenso y % de veces que cada partido llega al consenso
En las tablas 4 y 5 se presentan los resultados de 30 simulaciones diferentes en 1-D y en 2-D respectivamente, con configuraciones iniciales no-aleatorias (descritas en la tabla 1), en donde se puede apreciar las diferentes dinámicas de los sistemas.
PARTIDOS |
|||||
% SITIOS AZULES |
ROJO |
AMARILLO |
VERDE |
AZUL |
PASOS TOTALES |
25 |
***** |
542 |
6205 |
1235 |
6306 |
30 |
4378 |
9754 |
164 |
***** |
9755 |
35 |
229 |
***** |
4614 |
1938 |
4615 |
40 |
496 |
***** |
81 |
1663 |
1664 |
45 |
***** |
82 |
11003 |
589 |
11004 |
50 |
597 |
***** |
370 |
2763 |
2764 |
55 |
126 |
1993 |
***** |
14422 |
14423 |
60 |
81 |
837 |
2330 |
***** |
2331 |
65 |
102 |
200 |
***** |
12773 |
12774 |
70 |
186 |
994 |
17 |
***** |
995 |
75 |
36 |
189 |
528 |
***** |
529 |
80 |
339 |
***** |
129 |
4879 |
4880 |
85 |
36 |
2 |
1734 |
***** |
1735 |
15.38% |
30.76% |
15.38% |
38.46% |
µ= 5675 σ=4776.44 |
|
Nota: ***** = llegó a consenso.
Pasos en que cada partido va “desapareciendo” en el sistema, pasos totales necesarios para llegar al consenso y % de veces que cada partido llega al consenso
PARTIDOS |
|||||
% SITIOS AZULES |
ROJO |
AMARILLO |
VERDE |
AZUL |
PASOS TOTALES |
25 |
80 |
525 |
1064 |
***** |
1065 |
30 |
299 |
250 |
564 |
***** |
565 |
35 |
1747 |
***** |
247 |
533 |
1748 |
40 |
***** |
289 |
37 |
533 |
534 |
45 |
170 |
192 |
1333 |
***** |
1334 |
50 |
802 |
399 |
73 |
***** |
803 |
55 |
***** |
438 |
122 |
385 |
439 |
60 |
202 |
366 |
162 |
***** |
367 |
65 |
222 |
80 |
277 |
***** |
278 |
70 |
56 |
1186 |
443 |
***** |
1187 |
75 |
160 |
70 |
1455 |
***** |
1456 |
80 |
64 |
10 |
93 |
***** |
94 |
85 |
154 |
63 |
93 |
***** |
155 |
15.38% |
7.69% |
0.00% |
76.90% |
µ= 771.15 σ = 536.51 |
|
Nota: ***** = llegó a consenso
Pasos en que cada partido va “desapareciendo” en el sistema, pasos totales necesarios para llegar al consenso y % de veces que cada partido llega al consenso
Al comparar estos resultados obtenidos, se observan diferencias significativas en el desarrollo de los agrupamientos o bloques de partículas del mismo estado (partido) así como el porcentaje de veces que una opinión llega al consenso. Se observa claramente como la evolución del sistema con configuración no-aleatoria en una dimensión, no se ve afectada en forma significativa por las condiciones iniciales; sin embargo, en el de dos dimensiones las condiciones iniciales si afectan al mismo. En la tabla 5 también se observa un punto “crítico” de cuando una opinión o estado con cierto porcentaje de miembros afiliados llega al consenso, siendo del orden de 55-60%.
Experimentos similares se realizaron para los programas en 2-D con 13 estados y 1- D con 10 y 15 estados. Se observó el mismo comportamiento que en el modelo anterior. [20] La simulación en 3-D se realiza en un cubo de 25 x 25 x 25.
CONCLUSIONES Y DISCUSIÓN
Los sistemas de partículas en interacción proporcionan una herramienta para analizar fenómenos de diferentes niveles de complejidad y campos, como son procesos sociales, expansión y difusión de fuego y rumor, dispersión de enfermedades, etc.
En este trabajo se presentó una generalización y análisis experimental de la interacción entre grupos de partículas aplicado a un fenómeno social específico: la pugna entre partidos a lo largo de un proceso de votación.
En conclusión se muestra cómo se puede simular un sistema de partículas en interacción particular: la conducta de voto, en donde:
a) La opinión de la partícula “x” al tiempo “t” cambia en razón del número de vecinos de opinión distinta a la suya entre el total de vecinos que tiene.
b) La interacción entre una partícula y sus vecinas es un fenómeno meramente local. Habrá mayor probabilidad de que adquiera una opinión contraria si se encuentra rodeada por una gran cantidad de partículas de otro partido.
c) La distribución de partículas semejantes al inicio del proceso puede ser un factor importante a considerar, entre más aleatoria sea esta distribución inicial, más difícil será llegar al consenso (debido a las posibilidades de comunicación o interacción entre sus miembros).
d) En los casos de dominancia cuantitativa se reproducen efectos como la aparición y casi desaparición de un partido, como ocurre en la política en el largo plazo (procesos de equilibrios políticos graduales).
e) Cuando un partido es muy fuerte tiende a mantener o aumentar su dominancia, como ocurre en situaciones reales.
f) El porcentaje de miembros de cada partido también es importante (aunque menos que el de la distribución).
g) En las simulaciones se puede observar que, bajo ciertas circunstancias, aparece el fenómeno de “minorías activas” ya mencionado; fenómeno que afecta sustancialmente los procesos políticos. [19]
h) En las diferentes simulaciones se mostró cómo ocurren situaciones que en el estudio de sistemas complejos aparecen en muy diferentes fenómenos: la transición de fase o de cambio crítico. [21,22]
Sobre este modelo es posible implementar otra serie de variables y elementos para hacer más rica la interacción del sistema colectivo. Por ejemplo, analizar la dinámica del mismo cuando a un estado determinado (partido o posición) se le da mayor peso de influencia; esto es, analizar la relación entre peso o fuerza del partido vs. la cantidad de adeptos al mismo. Otro ejemplo a experimentar podría ser analizar el efecto de la constitución de alianzas entre partidos; esto es, que dos partidos (A y B) se puedan fusionar en un tercero (C), bajo ciertas circunstancias, como sería cuando les queden menos del 20% de miembros; y ver cómo estas alianzas afectan la evolución del sistema (si logran el consenso a pesar de la desventaja numérica).
Este modelo puede representar una opción para formalizar el estudio de fenómenos complejos en situaciones acotadas, en donde las partículas se ven influenciadas sólo por sus vecinos más cercanos. El caso de modelos para dimensiones mayores a 2 sigue siendo complicado, es necesario seguir trabajando y mejorando este tipo de modelos debido a que estos últimos se aproximan más a los fenómenos reales. En este sentido, cabe mencionar los avances que se han logrado en este campo del IPS mediante la mejora de estos algoritmos en diferentes fenómenos. Ejemplos de ello, son los trabajos presentados en la Escuela del Instituto Isaac Newton en U. K., con el tema “Non- equilibrium dynamics of Interacting Particles Systems”, en marzo-abril de 2006 (programa y abstracts en: <http://www.newton.cam.ac.uk/programmes/PDS/pdsw02.html> y los trabajos más recientes de <Durrett> y cols. [4,6,23,24] y <Liggett> [3,10].
REFERENCIAS
[1] Liggett, T. (1985). Interacting Particle Systems (New York: Springer, Series of Comprehensive Studies in Mathematics, 276). Se reimprimió en Heidelberg/Springer Berlin, 2005 (en su serie Classics in Mathematics).
[2] Durrett, R. (1995). Ten Lectures on Particle Systems, Lecture Notes in Mathematics
1608 (Heidelberg/Springer Berlin).
[3] Liggett, T. M. (2002). “Interacting Particle Systems — An Introduction”. Conferencias impartidas en la Escuela y Conferencia sobre Probability Theory en el International Center for Theoretical Physics, Trieste, mayo 13-17. [En línea]. Disponible en:
<http://users.ictp.it/~pub_off/lectures/lns017/Liggett/Liggett.pdf>, consulta: febrero 20 de 2008.
[4] Cox, J. T., R. Durrett & E. A. Perkins. (2000). “Rescaled voter models converge to super-Brownian motion”, The Annals of Probability, Institute of Mathematical Statistics, Ithaca, New York, USA, vol. 28, no. 1, pp. 185-234.
[5] Durrett, R. (1981). An introduction to Infinite Particles Systems, Stochastic Processes and their Applications, St. Louis, MO, USA: Elsevier, no. 11, pp. 109-150.
[6] Durrett, R. & Paul Jung. (2007). “Two phase transitions for the contact process on small worlds”, Stochastic Processes and their Applications, no. 117, pp. 1910-1927, [En línea]. Disponible en: <http://www.math.cornell.edu/~durrett/smw/smallworld0308.pdf>, consulta: febrero 18 de 2008.
[7] Dorogovtsev, S. N. (2006). “New critical phenomena in complex networks”, Taller del Issac Newton Institute: Non-equilibrium Dynamics of Interactive Particles Systems, GB, 27 marzo- 7 abril, resumen [en línea]. Disponible en:
<http://www.newton.cam.ac.uk/programmes/PDS/Abstract2/dorogovtsev.html>, consulta: febrero 18 de 2008.
[8] Durrett, D. & E. A. Perkins. (1999). “Rescaled contact processes converge to super- Brownian motion in two or more dimensions”, Probability Theory and Related Fields, New York: Springer, no. 114, pp. 309-399.
[9] Wagner, A. B. & Venkat Anantharam. (2002). “Designing an Interacting Particle System: Optimization of the Piecewise-Homogeneous Contact Process”, 2002 Conference on Information Science and Systems, Princeton University, USA, marzo 20-
22. [En línea]. Disponible en:
<http://www.eecs.berkeley.edu/~ananth/2002+/Aaron/cisspaper.pdf>, consulta: diciembre 12 de 2007.
[10] Liggett, T. M. (1997). “Stochastic models of interacting systems”, The Annals of Probability, Institute of Mathematical Statistics, Ithaca, New York, USA, vol. 25, no. 1, pp. 1-29.
[11] Cox, T. & Griffeath, D. (1986). “Diffusive clustering in the two dimensional voter model”, The Annals of Probability, Institute of Mathematical Statistics, Ithaca, New York, USA, no. 14, pp. 347-370.
[12] Mayol Cuevas, W.; Fernández Liz, J.; Vargas-Medina, E. & Figueroa-Nazuno, J. (1991). “Análisis de la dinámica de un sistema de partículas en interacción en 1 y 2D”, XXXIV Congreso Nacional de Física, 21-25 de octubre, resumen publicado en: Suplemento del boletín de la Sociedad Mexicana de Física, 5-2.
[13] De Alba González, M.; Vargas-Medina, E., Contreras Ibáñez, C. & Figueroa-Nazuno,
J. (1989). “Modelo de votación: un modelo para el estudio de partículas en interacción en 1, 2 y 3 dimensiones”, XXXII Congreso Nacional de Física, León, Gto., México, 23-27 de octubre.
[14] Canto, J. M. y Gómez, L. (1996). “Influencia social en el cambio de los estereotipos”,
Psicothema, vol. 8, no. 1, pp. 63-76. [En línea]. Disponible en:
<http://redalyc.uaemex.mx/redalyc/pdf/727/72780105.pdf>, consulta: diciembre 22 de 2007.
[15] Canto, J. M., Navarro, C. y Fraegel, H. (2000). “Actitudes políticas, autoposicionamiento ideológico y conducta de voto”, en A. Ovejero, M. M. Moral y P. Vivas. Aplicaciones en psicología social. Madrid: Biblioteca Nueva.
[16] Durrett, R. (1988). “Crabgrass, Measles and Gypsy Moths: An introduction to Interacting Particle Systems”, The Mathematical Intelligencer, New York: Springer, vol. 10, no. 2, pp. 37-47.
[17] Durrett, R. (1989). “Lecture Notes on Particle Systems and Percolation”, (Wadsworth, Belmont, CA).
[18] González, L. y Canto, J. M. (1995). “La influencia minoritaria en psicología social: apuntes para una reconstrucción histórica”, Revista de Psicología Social, Universidad de La Rioja, España, vol. 10, no. 1, pp. 75-99.
[19] Salgado Lévano, A. C. (2006). “Conceptualización sobre psicología política y una mirada a sus investigaciones durante los últimos años”, Liberabit. Revista de Psicología, Universidad de San Martín de Porres, Perú, no. 12, pp. 95-106. [En línea]. Disponible en:
<http://redalyc.uaemex.mx/redalyc/pdf/686/68601210.pdf>, consulta: enero 12 de 2008.
[20] Mayol Cuevas, W.; Fernández Liz, J.; Vargas-Medina, E. & Figueroa- Nazuno, J. (1993). “Un modelo matemático y su simulación de un proceso de participación social: el voto”, III Congreso Nacional de Psicología Social, México, D. F., México, 15-18 de junio.
[21] Martin, O. C., Monasson, R. & Zecchina, R. (2001). “Statistical Mechanics Methods and Phase Transitions in Optimization Problems”, Theoretical Computer Science, New York, USA: Elsevier, vol. 265, no. 1-2, pp 3-67.
[22] Figueroa Nazuno, J. y E. Vargas Medina (1992). “Los sistemas complejos: una nueva forma de análisis en las ciencias contemporáneas”, en: Campos, Miguel Ángel, y Roberto Varela (eds.), Prospectiva social y revolución científico-tecnológica, México: UNAM-UAM, pp. 73-79.
[23] Durrett, R. & C. Neuhauser (1994). “Particle systems and reaction diffusion equations”, The Annals of Probability, Institute of Mathematical Statistics, Ithaca, N. Y., USA, no. 22, pp. 289-333.
[24] Cox, J. T., R. Durrett & E. A. Perkins. (1999). “Rescaled particle systems converging to super-Brownian motion”, en M. Bramson & R. Durrett, editors, Perplexing Problems in Probability: Festschrift in Honor of Harry Kesten, Birkhäuser, Basel.