Revista del Centro de Investigación de la Universidad La Salle
Vol. 13, No. 52, julio-diciembre 2019, pp. 19-66
DOI: http://doi.org/10.26457/recein.v13i51.1925

Diseño de rutas de recolección utilizando el algoritmo de optimización por colonia de hormigas

Design of collection routes using the ant colony optimization algorithm

Francisco Javier Márquez Cortés¹, Katya Rodríguez-Vázquez², Beatriz Aurora Garro Licón³

¹Facultad de Ciencias – UNAM (México)
²IIMAS-UNAM (México)
³IIMAS-UNAM (México)

Correspondencia del autor: franciscomarquez@ciencias.unam.mx

Recibido: 03 de junio de 2019 | Aceptado: 18 de noviembre de 2019 | Publicado: 03 de junio de 2020 |

Copyright © 2019 "Francisco Javier Márquez Cortés, Katya Rodríguez-Vázquez & Beatriz Aurora Garro Licón." This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

---

Solid waste management is a very relevant problem in densely populated cities such as Mexico City. In Mexico it is common that a collection truck passes in front of each home to take away the waste. The routes that the trucks follow to collect the waste have been empirically designed by the drivers operators, which are affected by other problems such as traffic, lack of personnel, blocked roads or repairs, among others. In this sense, it is necessary to look for new techniques that help improve this form of collection without affecting the citizens, and also, that reduce the travel times and the distance traveled with respect to the current routes. This research describes a methodology based on swarm intelligence techniques aimed to design optimal routes, seeking to improve the management of waste collection and reduce operating costs. Particularly, a technique based on the behavior of ants known as Ant Colony Optimization (ACO) is used. To achieve this, first, the graph corresponding to the geographical area of interest is obtained; a transformation is carried out immediately to obtain an instance of the arc routing problem, that is, a graph that best represents the area and its restrictions; on that graph the ACO technique is applied to obtain new routes. The performance of the proposed methodology was evaluated in the streets of the Villa Milpa Alta neighborhood, one of the twelve towns belonging to the Milpa Alta mayor's office in Mexico City, the routes obtained were compared with the routes currently used by the truck collector. The results showed that it was possible to reduce the distances and travel time to the collection trucks.

Keywords: Ant Colony Optimization, Solid waste collection

Resumen

---

El manejo de residuos sólidos es una problemática muy relevante en ciudades densamente pobladas como la Ciudad de México. En México se tiene la costumbre de que el camión recolector pase frente a cada hogar para llevarse los residuos. Las rutas que siguen los camiones para recoger los residuos han sido obtenidas de manera empírica por los mismos operadores, las cuales se ven afectadas por otras problemáticas como tráfico, falta de personal, vialidades bloqueadas o en reparación, entre otras. En este sentido, es necesario buscar nuevas técnicas que ayuden a mejorar esta forma de recolección sin afectar a los ciudadanos, y, además, que reduzcan los tiempos de traslado y la distancia que se recorre con respecto a las rutas que se utilizan de forma cotidiana. En este artículo, se describe una metodología basada en técnicas de inteligencia colectiva para el diseño óptimo de rutas, buscando así mejorar el manejo de la recolección de residuos, disminuir costos de operación y obtener un conjunto de rutas posibles a seguir. Particularmente, se utilizará una técnica basada en el comportamiento de las hormigas cuando están en busca de alimento conocida como Optimización por colonia de hormigas (ACO por sus siglas en inglés). Para lograr esto, primeramente, se obtendrá el grafo correspondiente a la zona geográfica de interés; en seguida se realizará una transformación para obtener una instancia del problema de ruteo por arcos, es decir, un grafo que represente mejor la zona y sus restricciones; sobre ese grafo se aplicará la técnica de ACO para obtener nuevas rutas. El desempeño de la metodología propuesta se evaluó en las calles de la colonia Villa Milpa Alta, uno de los doce pueblos perteneciente a la alcaldía Milpa Alta de la Ciudad de México, las rutas obtenidas fueron comparadas con las rutas que actualmente son utilizadas por el camión recolector. Los resultados mostraron que era posible reducir las distancias y tiempo de traslado a los camiones recolectores.

Palabras clave: Optimización por colonia de hormigas, recolección de residuos sólidos.

Introducción

---

La contaminación es una de las problemáticas más grandes alrededor del mundo. En ciudades densamente pobladas como la Ciudad de México, la generación de residuos sólidos es uno de los principales factores contaminantes. Actualmente, se producen alrededor de 12,893 toneladas de basura por día por lo que es muy importante contar con los medios y técnicas adecuadas para poder disponer de todos esos residuos de manera adecuada.

El manejo de la basura generada por las viviendas en la ciudad, se ve afectado por otras problemáticas como tráfico, falta de personal, vialidades bloqueadas o en reparación, entre otras. Además, en México se tiene la costumbre de que el camión recolector pase frente a cada hogar para llevarse los residuos, por lo que sería difícil que los usuarios acepten otra forma de deshacerse de su basura. Debido a esto, se deben de buscar nuevas técnicas que ayuden a mejorar esta forma de recolección sin afectar a los ciudadanos, y, además, que reduzcan los tiempos de traslado y la distancia que se recorre con respecto a las rutas que se utilizan de forma cotidiana.

Hablando de movilidad, en la Ciudad de México, no es fácil encontrar una buena ruta para desplazarse de un lugar a otro ya que continuamente enfrentamos problemas como manifestaciones, inundaciones, obras, fiestas y celebraciones, embotellamientos, etc. Esto no solo incrementa los tiempos de traslado, sino que aumenta los gastos de operaciones y cambia constantemente las mejores rutas para transitar. En ese sentido, tener una herramienta que auxilie en la búsqueda de rutas en determinados momentos, sería de gran ayuda para los camiones recolectores que tienen que lidiar con estos problemas diariamente para poder proporcionar el servicio de recolección a todos los ciudadanos.

Actualmente, la ruta que siguen los camiones para recoger los residuos ha sido obtenida de manera empírica por los mismos operadores. Es por ello que aplicar técnicas computacionales para el diseño óptimo de rutas puede mejorar el manejo de la recolección de residuos, disminuir costos de operación y obtener un conjunto de rutas posibles a seguir que serán las mejores bajo ciertas condiciones.

En el año de 1992 Marco Dorio propuso una técnica para obtener una ruta óptima en un grafo (Dorio and Stützle, 2004); dicha técnica estaba basada en el comportamiento de las hormigas cuando están en busca de alimento. Esta técnica es conocida como Optimización por Colonia de Hormigas (ACO por sus siglas en inglés). A partir de su publicación han aparecido bastantes soluciones a problemas en grafos, uno de estos problemas es el llamado “problema del cartero chino” el cual nos pide encontrar una ruta que minimice tiempo y distancia para entregar la correspondencia en todas las calles de una ciudad. Para este tipo de problemas no existe algoritmo que pueda encontrar una solución en tiempo polinomial debido a que es un “problema NP-Duro”; sin embargo, utilizando ACO, se puede obtener una muy buena solución relativamente en poco tiempo. El problema de ruteo de vehículos por arcos (CARP, por sus siglas en inglés) consiste en satisfacer las demandas sobre los arcos de un grafo mediante uno o varios vehículos con capacidad limitada, los cuales inician su recorrido en un depósito y finalizan en el mismo. Además, se requiere que el recorrido que realicen los vehículos sea mínimo, es decir, que de todas las opciones posibles, la ruta escogida por el vehículo tenga la menor distancia, tiempo, o cualquier otra variable considerada en la función objetivo.

Diferentes autores han buscado resolver el problema de optimización y recolección de residuos mediante diferentes técnicas como búsqueda tabú (Angelelli and Speranza, 2002) y optimización por colonia de hormigas con un enfoque VRP (Liu and He, 2012; Otoo et al., 2014; Aynodkar and Bhosale, 2015; Xue and Cao, 2016; Ismail and Loh, 2009).

El problema CARP simula de una muy buena manera al problema de recolección en las ciudades, debido a que se tiene una flota de vehículos, los cuales tienen una capacidad limitada y a su vez deben brindar su servicio en los arcos de un grafo, lo que equivale a las calles de la ciudad. En ese sentido, el problema que se busca resolver es optimizar los recorridos que pueda seguir un vehículo en un proceso de recolección de residuos para encontrar la mejor ruta, logrando así mejorar la distribución de los camiones recolectores y, por ende, mejorar el servicio.

Lacomme y otros (2004b) presentan una aplicación de una colonia de hormigas al problema CARP. La particularidad de esta propuesta es que utiliza dos tipos de hormigas, las elitistas que se encargan de que la solución converja a un mínimo y las no elitistas que se encargan de explotar el espacio de búsqueda para evitar caer en mínimos locales. En (Longo et al., 2006) se propone una técnica de solución para el CARP en la que cada arco se reemplaza por dos vértices para convertir el problema a una instancia de CVRP, la restricción es que los vértices que forman un arco deben ser visitados de manera consecutiva para simular el recorrido por el arco original. Para resolver este VRP se utilizó la técnica de Branch and cut and Price (Fukasawa et al., 2006). En (Lacomme et al., 2004a) se extiende al CARP con restricciones más realistas como la prohibición de ciertas vueltas o la aplicación de un servicio en ambos lados de la calle. En (Vidal, 2017), se probaron 1528 instancias de 18 distintos benchmarks utilizando la búsqueda local iterada (Prins, 2009) y búsqueda genética hibrida unificada (Vidal et al., 2014) en distintos tipos de problemas de ruteo como el CARP, NEARP, NEARP con restricción en las vueltas, PCARP entre otros.

Entre las aportaciones principales de esta investigación se puede mencionar que se resuelve una problemática social real que no había sido abordada hasta ahora, la cual busca generar un beneficio directo para la sociedad a partir de mejorar el servicio de recolección de residuos, mejorando las rutas que se utilizan actualmente en una colonia representativa de la alcaldía Milpa Alta, reduciendo el tiempo de traslado entre los distintos viajes que realizan los camiones recolectores, minimizando la distancia total de recorrido para cada camión y minimizando los costos de operación, sentando así un precedente en la aplicación de estas técnicas para resolver problemáticas similares que se presentan en la ciudad.

El objetivo que tiene esta investigación es encontrar la mejor ruta o una muy buena aproximación para resolver el problema de la recolección de residuos. Este problema será planteado como una instancia del problema de ruteo por arcos (ARP por sus siglas en inglés) en un grafo, para lo cual se realizará la implementación de la metaheurística de optimización por colonia de hormigas. Además, se tomarán en cuenta algunas de las restricciones con las que se realiza dicha actividad y se considerarán tiempos promedio de carga y descarga en los camiones. Particularmente, se buscará mejorar las rutas de recolección de residuos sólidos en uno de los doce pueblos pertenecientes a la alcaldía Milpa Alta (Villa Milpa Alta) tomando como criterio el reducir distancias y tiempo de traslado a los camiones recolectores. Para lograr esto, primeramente, se obtendrá el grafo correspondiente a la zona geográfica sobre la que se desea trabajar (en este caso, las calles de la colonia Villa Milpa Alta); en seguida se realizará una transformación para obtener una instancia del problema de ruteo por arcos, es decir, un grafo que represente mejor la zona y sus restricciones; sobre ese grafo se aplicará la técnica de ACO para obtener nuevas rutas.

1. Conceptos básicos

---

En esta sección, se describirán los conceptos necesarios para entender la base de esta investigación, para comprender la metodología y los resultados obtenidos. Particularmente, se realizará acercamiento a la teoría de grafos, se explicará en que consiste el problema de ruteo de vehículos y sus variantes, así como la definición de optimización y los diferentes algoritmos basados en la optimización por colonia de hormigas.

2. Teoría de Grafos

---

De manera sencilla, podemos ver a un grafo como un conjunto de puntos y otro de flechas o líneas, las cuales conectan a los puntos entre sí dada una relación común entre ellos. Los puntos reciben el nombre de vértices o nodos y las flechas se llaman adyacencias. Los vértices pueden representar cualquier objeto o entidad como personas, ciudades, números o estaciones en una red; mientras que las adyacencias representan las relaciones que existen entre ellos, como pueden ser la amistad entre un conjunto de personas, donde algunas conexiones serán más fuertes que otras, los diferentes caminos que puede haber entre un conjunto de ciudades, la relación matemática entre dos o más valores, etc. Para representar la relación entre dos vértices cualesquiera, normalmente se utilizan tuplas de la forma $(a,b)$ donde $a$ y $b$ son vértices; esto se puede leer como “$a$ está relacionado con $b$”.

Formalmente, un grafo $G$ se representa como $G = (V,E)$ donde $V$ es un conjunto de elementos llamados vértices y $E$ es un subconjunto de elementos del producto cartesiano $V \, \mathrm{X}\, V$, de modo que $E\subseteq V \, \mathrm{X}\, V$ y representa las adyacencias (Berge, 1970). Cada vértice presenta un valor asociado llamado grado, el cual indica la cantidad de adyacencias que inciden en él. Como las adyacencias representan la relación entre cualesquiera dos vértices $a$ y $b$, puede suceder cualquiera de los siguientes casos:

• $a$ está relacionado con $b$ pero $b$ no está relacionado con $a$.
• $a$ está relacionado con $b$ y, al mismo tiempo, $b$ esta relacionado con $a$.
• $a$ esta relacionado con $b$ pero $b = a$.

Dado las relaciones anteriores se tienen tres tipos de adyacencias: los arcos, las aristas y los lazos.

Un arco es una adyacencia en la cual la dirección de la relación está definida de manera explícita (Berge, 1970). Por esto, un arco representa el primer caso. Para verlo de manera gráfica se utiliza una flecha que indica el sentido de la relación.

Siguiendo la definición de Berge, una arista representa el segundo caso, e indica que la relación se da en ambos sentidos ya que no hay dirección explícita. Para representarla, se utiliza una simple línea o una flecha bidireccional.

Berge define a un lazo (también le llama bucle) como la relación que tiene un vértice consigo mismo. Se utiliza una flecha o línea que empieza y termina en el mismo vértice para representarlo.

Berge clasifica a los grafos de acuerdo al tipo de adyacencias que presentan; los grafos dirigidos son aquellos en los que las relaciones entre vértices están denotadas por arcos, es decir, todas tienen dirección específica. Los grafos no dirigidos, por el contrario, no presentan dirección en ninguna de sus adyacencias, es decir, todas son aristas. Por último, tenemos los grafos mixtos que, como su nombre lo indica, presentan arcos y aristas por igual. Las adyacencias a su vez, pueden tener un valor asociado llamado peso, en caso de no indicar un peso, se tomará el valor de 1.

Sean $x$, $y$ vértices (no necesariamente distintos) de un grafo no dirigido $G = (V,E)$.

1. Un camino $x-y$ en $G$ es una sucesión alternada finita sin lazos $W$ tal que $W=\left \{ x=v_{0} ,e_{1},v_{1},e_{2},v_{2},...\, ,e_{k},v_{k}\, =y\right \}$, cuyos términos son vértices y adyacencias de manera alternada de modo que, $e_{1}=(v_{1}-1,v_{1})$ con $1\leq i\leq k$.
2. La longitud de un camino es $k$, donde $k$ es el número de adyacencias que contiene el camino. Si $k=0$ entonces es un camino sin aristas y $x=y$. A este camino se le denomina trivial.
3. Cualquier camino donde $x=y$ es un camino cerrado. Esto quiere decir que empieza y termina en el mismo vértice, si no sucede así, el camino es abierto.
4. Sea $W$ un camino $x-y$ en un grafo $G$, si no se repite ninguna adyacencia en $W$ entonces el camino es un recorrido $x-y$.
5. Un recorrido $x-x$ cerrado es un circuito.
6. Si ningún vértice del camino $x-y$ se presenta más de una vez, el camino es un camino simple $x-y$.
7. Un ciclo consiste en un camino simple $x-x$.

Una vez que se tiene la representación de un grafo podemos recorrerlo a través de sus aristas. Existen diversos nombres para la forma y las restricciones de cada recorrido, los más famosos son el circuito Euleriano y el ciclo Hamiltoniano.

3. Optimización por Colonia de Hormigas

---

Cuando se toma una decisión siempre se busca que sea la mejor, pero, ¿cómo sabemos que es realmente la mejor? Para tener certeza en esto, tendríamos que conocer todas las posibles opciones y compararlas una a una para determinar si realmente es la mejor o no. Este proceso al cual todos nos hemos enfrentado al menos una vez en la vida se le llama optimización. La optimización es el acto de obtener el mejor resultado posible bajo ciertas circunstancias (Astolfi, 2006). Es el proceso de determinar la mejor opción (Parkinson et al., 2013). La optimización es una técnica ampliamente usada en la Investigación de Operaciones que ha sido empleada en muchas aplicaciones. El objetivo es maximizar o minimizar una función sujeta a un conjunto de restricciones tanto de igualdad como desigualdad.

Sea $\pi$ un problema de optimización, una instancia de $\pi$ es una tripleta $(S,f,\Omega)$ donde $S$ es el conjunto de soluciones candidatas, $f$ es la función objetivo que asigna un valor $f(s)$ a cada $s\, \in\, S$, y $\Omega$ es el conjunto de restricciones. Las soluciones que satisfacen a todas las restricciones en $\Omega$ se llaman soluciones factibles y se representan como el conjunto $\tilde{S}\, \subseteq S$. El objetivo es encontrar una solución factible $s^{*}\in \, S$ de modo que, si el problema es de minimización, $f(s^{*})\leq f(s)\forall s\in\tilde{S}$ (Dorigo and Stützle, 2004). Un ejemplo podría ser encontrar al máximo global de una función matemática $f:\mathbb{N}\rightarrow \mathbb{N}$, el conjunto de posibles soluciones corresponde al dominio de la función $\mathbb{N}$, pero encontrar el valor que maximiza la función requiere evaluar todos los posibles elementos del dominio o aplicar técnicas de cálculo.

Cuando se dice que un problema es de optimización combinatoria, se refiere al hecho de que el dominio de la función objetivo es finito o es numerable. A los problemas de optimización combinatoria también se les conoce como problemas de optimización discreta. Algunos de los problemas de optimización combinatoria más famosos en la computación son: problema del agente viajero (Chvátal et al., 2010), problema del cartero chino (Kwan, 1962), problema de la mochila (Martello and Toth, 1990) y coloración de grafos (Ufuktepe and Bacak Turan, 2005). Para resolver este tipo de problemas utilizando una computadora se aplican varias técnicas, una de ellas son los algoritmos evolutivos los cuales utilizan funciones heurísticas.

De acuerdo con (Russell and Norvig, 2010), una función heurística $h(n)$ estima el costo de una solución a partir de un estado $n$. Se dice que una heurística es la aplicación de toda la información que se tiene de una instancia de un problema que permite encontrar una solución aproximada en menos tiempo del necesario para encontrar una solución óptima; al ser creada para una instancia en particular, no garantiza su efectividad en otras instancias. Además, la calidad de la solución es variable y puede ser muy buena en algunos casos y mala en otros.

Una vez que se ha definido una heurística, es muy difícil tener una heurística distinta para cada problema que se presente, pero también, algunas heurísticas se pueden reusar en otros problemas, ya que su planteamiento no tiene nada que ver con la instancia del problema en sí. De esta manera surgen las metaheurísticas, que se definen como: un proceso de generación iterativa que guía a una heurística subordinada al combinar de manera inteligente distintos conceptos de exploración y aprovechamiento del espacio de búsqueda, se utilizan estrategias de aprendizaje para estructurar la información a modo de encontrar soluciones cercanas a la óptima (Osman and Laporte, 1996). Otra definición de metaheurística es: el conjunto de conceptos algorítmicos que pueden ser usados para definir métodos heurísticos aplicables a un conjunto de problemas. (Dorigo and Stützle, 2004).

Existen varios ejemplos de metaheurísticas, entre los más famosos se encuentran los algoritmos evolutivos, los cuales son un método de búsqueda probabilista que actúa sobre una población de soluciones simulando, a un nivel de abstracción alto, la evolución de las especies en la naturaleza (Pereira and Tavares, 2009). Dentro de los algoritmos evolutivos se encuentran a los algoritmos genéticos (Holland, 1992), programación genética (Koza, 1992) y colonia de hormigas (Dorigo and Stützle, 2004). Todas estas técnicas han sido aplicadas a una gran diversidad de problemas de manera satisfactoria porque no fueron creadas pensando en resolver un problema en particular, sino más bien como una herramienta que permita optimizar la codificación recibida, por lo que basta poder transformar algún problema a la forma requerida por alguna de estas técnicas para utilizarla.

Las hormigas son uno de los insectos que más han llamado la atención de las personas debido a su comportamiento social. Una de las habilidades más sorprendentes que tienen es la de encontrar un camino de su hormiguero hacia alguna fuente de alimento. Si bien una sola hormiga no podría hacerlo por sí misma, es la cooperación de todas ellas para lograr un bien común lo que hace la diferencia en la búsqueda. El objetivo de un algoritmo de hormigas es la solución de problemas de optimización a partir de la simulación de las técnicas utilizadas por dichos animales en la solución de problemas de su entorno.

Algunos comportamientos que han motivado a los algoritmos de colonia de hormigas son: exploración, división de tareas y transporte colectivo. Estas actividades las realizan mediante la estigmergia, que es un concepto introducido por el biólogo Pierre-Paul Grasse en el año de 1959 y habla sobre una forma de comunicación mediante la modificación del ambiente. Como resultado de esa definición podemos decir que la idea detrás de un algoritmo de hormigas es el uso de una estigmergia artificial para coordinar agentes artificiales (Dorigo, 1992).

La optimización por colonia de hormigas (ACO, por sus siglas en inglés) es una metaheurística de optimización combinatoria que consta de agentes artificiales basados en hormigas que al simular su comportamiento cooperativo permiten resolver una gran variedad de problemas de teoría de grafos (Dorigo and Stützle, 2004). La idea básica consiste en que, por cada iteración, cada hormiga construya una propuesta de solución y deje un rastro de feromona inversamente proporcional al costo que conlleva dicha solución; la feromona incrementará la probabilidad de que otras hormigas sigan esa misma ruta y en cada iteración la feromona total de la instancia disminuirá en un factor constante, de modo que las soluciones más cortas tengan mayor concentración de feromona. La solución aceptada será aquella en la que el costo sea menor. Esta técnica fue desarrollada por Marco Dorigo en su tesis doctoral en 1992 (Dorigo, 1992) y su desarrollo comenzó al observar los resultados de los experimentos de doble puente sobre hormigas (Goss et al., 1989b).

Al querer modelar este comportamiento por medio de la computadora, se hicieron algunos ajustes y se construyó la primera variante de ACO llamada Ant System, orientada a obtener rutas mínimas y a atacar el problema del agente viajero. El algoritmo aplicado a un grafo es bastante sencillo, el primer paso es inicializar la feromona $\tau_{ij}$ de cada arco o arista, por lo general se utiliza el valor de 1 aunque depende totalmente del problema. Después, cada hormiga se pone en modo búsqueda o forward lo que significa que va a explorar el espacio de búsqueda hasta encontrar una solución, y una vez que se construyó una solución se eliminan los posibles ciclos encontrados, se cambia el modo búsqueda de la hormiga y se toma su camino de regreso, depositando feromona en cada adyacencia que conforma la propuesta de solución encontrada. Las acciones locales son opcionales y la mayoría de las veces se aplican otros procedimientos como búsqueda local para intentar mejorar aún más las soluciones generadas por ACO.

Sea $k$ una hormiga, la construcción de la solución consiste en que $k$ parte del vértice origen $v_{0} y$, mientras no haya llegado al vértice destino $v_{f}$ , recorre por los distintos vértices para construir una ruta. Si $k$ se encuentra en el vértice $i$, la probabilidad $p_{ij}^{k}$ (probabilidad de que $k$ avance al vértice $j$) está dada por:

Donde $N$ es el vecindario del vértice $i$, es decir, todos los vértices que comparten una adyacencia con $i$ sin incluir al vértice anterior en el recorrido de $k$, a menos que no tenga más vecinos en cuyo caso, debemos regresar sobre nuestro recorrido para evitar estancarnos. Esta construcción puede generar ciclos en el camino por lo que es necesario eliminarlos para conservar el recorrido necesario de la hormiga $k$ para evitar que se deposite feromona de manera inútil. Cada que una hormiga se mueve de un vértice a otro se aplica la fórmula de actualización de feromona $\tau_{ij}\leftarrow (1-\rho )\tau_{ij},\forall (i,j)\in A$ para simular la evaporación de feromona. Cuando la hormiga k logra construir una solución debe actualizar la feromona de la siguiente manera:

Donde $\Delta \tau ^{k}$ es la feromona que la hormiga k deposita.

4. Problema de ruteo de vehículos

---

Los problemas de ruteo son aquellos que conciernen la distribución de bienes y/o servicios entre depósitos y usuarios finales llamados clientes, los cuales se encuentran en una red de caminos en la que dichos servicios serán brindados por una flota de vehículos en un periodo de tiempo específico (Toth and Vigo, 2001). En los últimos años han cobrado relevancia debido a su aplicación en distintas áreas y al impacto positivo que han tenido, sobre todo en logística. Algunos ejemplos de situaciones que pueden ser modeladas como un problema de ruteo son: limpieza de calles, búsqueda de rutas para transporte público, repartidor de combustible, etc.

Los problemas de ruteo constan de 4 partes esenciales para su definición: los clientes, los vehículos, la función objetivo y la red sobre la cual se desarrolla el problema (Rizzoli et al., 2004).

La red representa todas las posibles rutas a seguir dependiendo de las restricciones en distancia, dirección y conexidad entre los distintos componentes del problema de ruteo. La forma más común es mediante un grafo. Se puede hacer una clasificación de problemas de ruteo según el tipo de grafo sobre el cual están representados, de modo que tenemos problemas de ruteo dirigidos, no dirigidos y mixtos. También en la red se ubican los depósitos, que son los lugares de donde parten los vehículos para iniciar su recorrido, se realiza la carga/descarga de la capacidad del vehículo y puede ser también el punto de regreso de estos.

Los clientes son los agentes que demandan su producto/servicio y tienen las siguientes características:

• • En general se encuentran en los vértices del grafo que representa la red de caminos, aunque pueden encontrarse en los arcos y/o aristas.
• Tienen una demanda $q_i$, la cual, debe ser recogida o satisfecha por el vehículo que los visite.
• Pueden tener una ventana de tiempo asociada $W=[w_0,w_1]$, que indica en que intervalos de tiempo pueden atender al vehículo.
• Pueden tener un valor asociado $t_i$ que indica el tiempo que toman en satisfacer su demanda/servicio.
• Si $T$ representa al conjunto de vehículos del problema, un subconjunto $T_{p}\subseteq T$ de modo que solo los vehículos que pertenezcan a él puedan atender sus peticiones.

A pesar de estar definidos de esta manera, a veces no es posible atender a todos los clientes por lo que, en muchos casos, también se les asigna prioridades o penalizaciones de acuerdo al servicio que solicitan.

Los vehículos son los encargados de llevar los bienes del depósito hacia los clientes a través de los posibles caminos en la red y tienen las siguientes características:

• Un depósito origen $d_0$ y pueden o no terminar su recorrido en ese depósito.
• Un valor $Q_i$ que indica la capacidad del vehículo $i$, este valor no debe ser sobrepasado en ningún momento.
• Sea $G=(V,E)$ el grafo asociado a un problema de ruteo, $E_{v}i\subset E$ el subconjunto de arcos asociado al vehículo $i$, que indica los arcos y/o aristas que puede recorrer.
• Un valor $C_i$ que indica el costo de usar el vehículo $i$.

La función objetivo modela algunas restricciones del problema de manera matemática buscando el valor mínimo o máximo posible al evaluar alguna solución candidata. La más utilizada es la minimización de distancia, aunque también se puede trabajar sobre el número de vehículos, el tiempo de servicio, el gasto de combustible, entre muchas otras (así como sus combinaciones). Las soluciones van a depender de la función objetivo que se decida usar y del número de variables a las que se aplica.

En la literatura se encuentran principalmente 3 problemas de ruteo, los cuales, han sido objeto de estudio por muchos científicos. Los problemas son los siguientes: El problema del agente viajero (TSP, por sus siglas en inglés), el problema de ruteo de vehículos (VRP, por sus siglas en inglés) y el problema del cartero chino (CPP, por sus siglas en inglés). Estos problemas son básicos y se les han aplicado bastantes extensiones para adecuarlos a las necesidades actuales y desarrollar nuevas técnicas que ayuden en la búsqueda de sus soluciones.

Hasta ahora los problemas mencionados se han formulado sobre vértices, pero existen también problemas cuyas restricciones obligan a cubrir los arcos o aristas de un grafo; estos problemas reciben el nombre de problemas de ruteo por arcos (ARP, por sus siglas en inglés). El estudio de este tipo de problemas se remonta a los orígenes de la teoría de grafos en el siglo XVIII, cuando Leonhard Euler estudió el famoso problema de los puentes de Königsberg. Este problema consistía en encontrar una ruta que comenzara en cierta parte del mapa, recorriera todos los puentes una vez sin repetirlos y regresara al punto de inicio, es decir, un ciclo Euleriano. Euler demostró que dicho recorrido era imposible y no solo eso, sino que, además, su análisis y demostración del problema se convertirían en la base de la formalización de la teoría de grafos.

El revuelo por este tipo de problemas volvió en 1962 con el estudio del problema del cartero chino (CPP, por sus siglas en inglés) por el matemático Mei-Ko Kuan (Kwan, 1962), el cual, consiste en encontrar la ruta que minimice la distancia recorrida por un cartero que tiene que entregar correspondencia por todas las calles del pueblo y que, al terminar, regrese a la oficina de correos. A diferencia de los anteriores problemas de ruteo, el CPP puede resolverse en tiempo polinomial si el grafo sobre el que se plantea es no dirigido, en otro caso no existe algoritmo que lo pueda resolver en tiempo razonable.

En la vida diaria se tienen problemas que, al transformarlos como una instancia de ruteo por vértices, resultan intratables o alteran la esencia original del problema. Un claro ejemplo sería el problema de encontrar la mejor ruta que debe seguir un camión recolector para recoger la basura de alguna colonia; los vértices serían las intersecciones entre calles, las aristas serían las calles en las que el camión debe realizar su trabajo y otras restricciones podrían ser: priorizar el servicio en un subconjunto de aristas o minimizar el número de aristas repetidas y asegurando que el camión pase por todas las calles de la colonia, es decir, que no deje ninguna arista del grafo sin recorrer.

¿Cómo se puede representar esto en un problema de vértices? La respuesta es que no se puede realizar, de modo que, se requiere otro modelo que permita plantear este problema de manera adecuada, por lo que se necesitan definir algunas variantes del problema de ruteo por arcos.

Al analizar los problemas reales y tratar de plantearlos como un ARP, se observa que entre más complejo sea el problema a resolver, más difícil es encontrar un modelo que permita representarlo con exactitud. Debido a esto, han surgido muchas variantes que parten del problema del cartero chino, por esto, es importante hacer la representación matemática formal del CPP.

De acuerdo a (Rabbani and Mohammadi, 2015), se tiene un grafo $G=(V,E)$ con $n=\left | V\right |$, el problema se puede plantear como un conjunto de ecuaciones matemáticas de la siguiente manera: Si $C_{ij}$ indica el costo de ir del vértice $i$ al vértice $j$ y $X_{ij}$ es el número de veces que se pasa del vértice $i$ al vértice $j$, lo que se busca es minimizar las veces que se pasa por cada arista para que el costo sea mínimo, o sea $min \sum\,_{i=1}^{n}\sum \, _{j=1}^{n}C_{ij}X_{ij}$.

También se debe de asegurar que cada vez que se visita cualquier vértice, debemos salir de él, por lo que la ecuación $\sum \, _{j=1}^{n}X_{ij}- \sum \, _{j=1}^{n}X_{ji}\forall i\in V$ es necesaria. Para asegurar que cada arista sea recorrida al menos una vez, se requiere que la desigualdad $X_{ij}+X_{ji}\geq 1\forall (i,j)\in E$ se cumpla. Por último, es necesario que el número de veces que se recorre cada arista sea un valor entero, esto es $X_{ij}\geq 0\forall i,j \in V X_{ij} \in \mathbb{Z}$.

Este problema puede ser resuelto en tiempo polinomial (Eiselt et al., 1995), lo que significa que existe un algoritmo que nos puede brindar una solución óptima en un tiempo razonable. Sin embargo, existen otras variantes que no pueden resolverse en tiempo polinomial (Lenstra and Kan, 1976), pero que vale la pena enunciar ya que al entender éstas, el análisis de algún otro tipo de problema de ruteo por arcos será más sencillo. Con respecto a las variantes del ARP, existen tantas como combinaciones de restricciones se puedan generar. Sin embargo, con entender estas variantes básicas se puede adentrar más en la teoría de los problemas de ruteo y comprender la mayor parte de los problemas planteados como tal. En (Corberán and Prins, 2010) se presentaron las siguientes variantes:

• Problema mixto del cartero chino (MCPP, por sus siglas en inglés). Dado un grafo mixto $G=(V,E)$ con pesos no negativos, encontrar una caminata cerrada de costo mínimo tal que pase por todas las aristas de $G$ al menos una vez.
• Problema ventoso del cartero (WPP, por sus siglas en inglés). Similar al MCPP excepto que $G$ es dirigida, por lo que ir de un vértice $A$ a un vértice $B$ puede tener un costo distinto que el recorrido de 4B$ hacia $A$. Como se puede apreciar, es una generalización del MCPP.
• Problema del cartero chino jerarquizado (HCPP, por sus siglas en inglés). Variante del CPP en la que se establece una relación de precedencia entre los diferentes subconjuntos en los que se divide el conjunto original de aristas. Dicha relación indica que si tenemos un subconjunto $E_i$ que precede a un conjunto $E_j$ entonces las aristas de $E_i$ deben recorrerse antes que las de $E_j$. En pocas palabras, se debe respetar el orden en el que las aristas deben ser recorridas de acuerdo a su prioridad. Puede resolverse de manera óptima en un tiempo razonable en casos muy especiales.
• Problema de máximo beneficio del cartero chino (MBCPP, por sus siglas en inglés). Se establece un valor de beneficio para cada arista $e \in E$ siendo $e_i$ el beneficio obtenido al pasar por la arista e la $i$-ésima vez. El objetivo es maximizar la suma de los beneficios al salir de un vértice $v$, recorrer todas las aristas y volver a $v$.
• Problema de ruteo por arcos con capacidad y no dirigido (UCARP, por sus siglas en inglés). Sea un grafo $G=(V,E)$ no dirigido, y sea $v_{i} \in V$ un vértice que funciona como depósito con $k$ vehículos idénticos los cuales tienen capacidad $Q$, además se asocia un costo $c_e$ a cada arista $\forall e \in E$ y por último se obtiene un subconjunto de aristas $E_{R} \subseteq E$ a las cuales se debe visitar. Cada arista tiene una demanda $q_{e}\geq 0$ y un costo de procesamiento $p_e$. El objetivo es encontrar un conjunto de rutas para los $k$ vehículos que minimicen el costo de servir a todas las aristas que pertenecen a $E_{R}$, de tal manera que cada ruta contenga el depósito y un conjunto de aristas que fueron recorridas por el vehículo de manera que la suma de la demanda de dichas aristas no exceda $Q$ (Eiselt et al., 1995).
• • Problema de ruteo por arcos con capacidad y ventanas de tiempo (DCARP, por sus siglas en inglés). Similar al UCARP, pero en un grafo dirigido (Eiselt et al., 1995).

Otra cosa importante es que el ARP se puede transformar a una instancia del VRP y viceversa, haciéndolos equivalentes (Yu, 2014). El método para transformar de VRP a CARP (Ghiani and Improta, 2000) consiste, a grandes rasgos, en construir un TSP generalizado, luego un TSP de clusters y después un TSP normal, el cual, puede ser resuelto mediante programación lineal.

5. Metodología propuesta

---

En esta sección se describe con detalle la metodología propuesta para diseñar nuevas rutas para la recolección de residuos sólidos mediante la optimización por colonia de hormigas. La metodología propuesta se divide en cuatro etapas las cuales se muestran en la Figura 1 y serán descritas en las siguientes secciones.

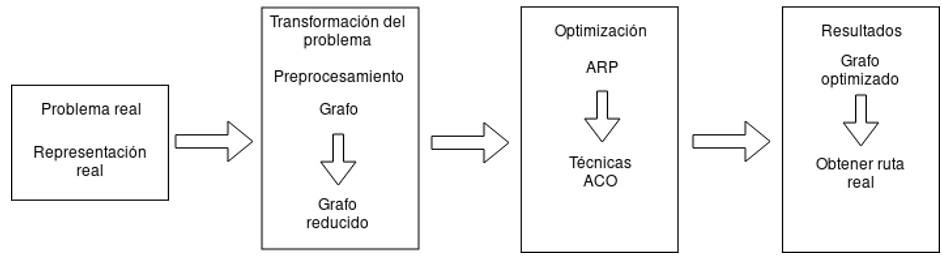Metodología propuesta

6. Delimitación de la zona de prueba

---

La Ciudad de México cuenta con una extensión territorial de 1,485 km cuadrados y se divide en 16 alcaldías con un total de 1863 colonias. En ella habitan 8,851,080 personas y se generan diariamente 12,920 toneladas de basura, lo que significa que cada habitante produce en promedio entre 0.86 y 2.44 kg de desechos. El origen de los residuos generados diariamente proviene principalmente de 3 fuentes: domicilios (48 %), comercios (26 %) y sector de servicios (14 %). Las alcaldías que más residuos generan son Iztapalapa, Gustavo A. Madero y Cuauhtémoc, aportando 41 % del total. Por otro lado, las alcaldías que menos residuos generan por día son Magdalena Contreras, Cuajimalpa y Milpa Alta aportando el 4 % del total.

En la Ciudad de México se cuenta con 2652 vehículos recolectores de los cuales 1698 son de carga trasera y de doble compartimiento, 155 rectangulares, 39 tubulares, 291 de volteo y 469 de otros tipos. Para realizar la operación de estos vehículos en las 1828 colonias donde se brinda el servicio, se cuenta con 6507 choferes y 1781 rutas de recolección.

Para el manejo de los residuos sólidos, la Ciudad de México cuenta con 12 estaciones de transferencia, 2 plantas de selección, 2 plantas compactadoras, 8 plantas de composta y 5 sitios de disposición final. Cada delegación se encarga de brindar servicios de limpia y recolección a sus colonias. Los camiones hacen un promedio de 2 viajes diarios para transportar la basura a las 12 estaciones de transferencia antes mencionadas. De acuerdo al Manual Técnico sobre generación, recolección y transferencia de residuos sólidos municipales (Secretaria de Desarrollo Social, 2001) los tres métodos más comunes de recolección de residuos son de parada fija, de acera y de contenedores.

La alcaldía Milpa Alta es la segunda demarcación más grande de la Ciudad de México, tiene una extensión territorial de 228 km cuadrados y se ubica al sureste de la ciudad. De acuerdo a datos del INEGI, Milpa Alta cuenta con una población de 115,895 habitantes siendo la alcaldía con menos personas en la Ciudad de México (Delegación Milpa Alta, 2017). En ella se generan 119 toneladas de basura al día correspondientes a 0.86 kg por habitante y cuenta con 58 vehículos recolectores, de los cuales 6 son de carga trasera, 9 de doble compartimiento, 27 de volteo y 16 de otras características. Milpa Alta brinda el servicio de recolección a 12 colonias, a través de 86 rutas distintas (Gobierno de la Ciudad de México, 2016). Cabe resaltar que el nivel de eficiencia en la recolección de residuos orgánicos de esta alcaldía es del 80 %, siendo la mejor de la ciudad en este ámbito.

7. Transformación del problema

---

Debido a que la alcaldía no contaba con un mapa actualizado de las calles donde se presta el servicio de recolección de residuos en Milpa Alta, se realizó una búsqueda de plataformas de terceros que permitieran el uso y descarga de sus mapas. Esta búsqueda solo arrojó una opción llamada OpenStreetMap contributors, la cual es una página web que proporciona mapas de todo el mundo y además permite descargar regiones delimitadas por el usuario. Estos mapas son editados por la comunidad y se permite el libre manejo de los mismos y los datos se pueden usar bajo la licencia de Open Database License.

El mapa descargado de la página web antes mencionada corresponde al pueblo de Villa Milpa Alta, véase Figura 2. La descarga se obtiene en un formato. son el cual resulta sencillo de manipular, ya que este guarda información relevante como nodos, caminos y distancias. Una vez realizada la descarga, se puede visualizar el mapa utilizando software específico, en nuestro caso, se utilizó Java Open Street Maps ya que no solo permite la visualización del mapa urbano, sino que además permite editar la información del mismo. Este software resulta crucial para el siguiente paso que consiste en eliminar información no necesaria del mapa para la solución de nuestro problema.

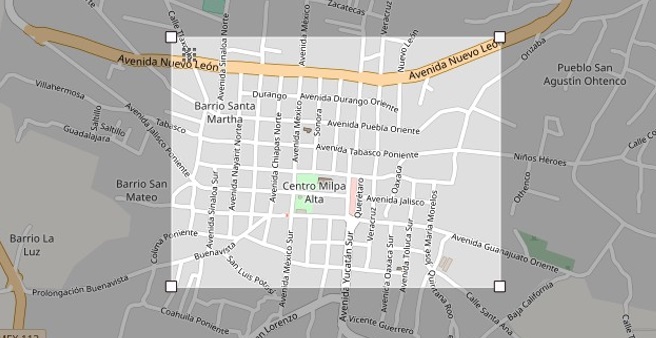Vista del mapa a descargar a través de OpenStreetMap

Para lograr obtener una representación matemática formal del problema, únicamente se tomará en cuenta la información necesaria para construirla, es decir, calles (arcos), intersecciones de calles (nodos o vértices) y las distancias entre cada intersección (pesos de cada arco).

Existen dos principales razones por las que se realizó una limpieza al mapa, la primera se debió al número excesivo de nodos utilizados para dar precisión a las calles, ya que se utilizaban sobre todo para representar curvas; si se reduce la cantidad de vértices en el grafo al mínimo, entonces reducirá la dimensión de la matriz de adyacencias. La otra razón es que existen muchas calles que se utilizaban como privadas, andadores, callejones, entre otras por lo que resultan imposibles de transitar para un camión recolector, es por esto que es innecesario considerarlas para la construcción de las rutas.

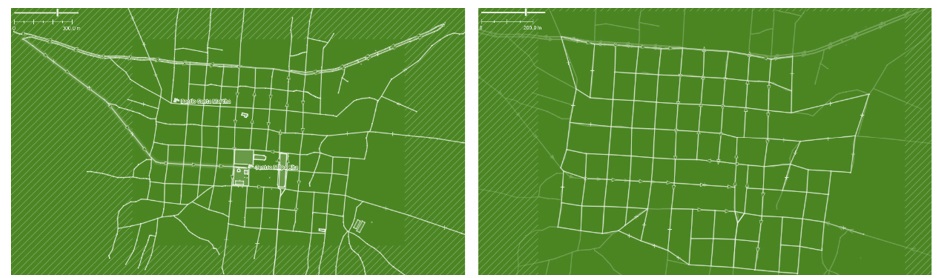Antes (izq.) y después (der.) de la eliminación de nodos de precisión

En la Figura 3 se observa el estado de una calle antes y después de eliminar los nodos de precisión. Con esta acción se pasa de tener cerca de 500 nodos a solo 105, siendo una reducción considerable en la magnitud del problema.

En el mapa de la Figura 4 se puede observar el resultado final de la limpieza del grafo, se aprecian mucho menos vértices o nodos. Por otro lado, las calles que no son necesarias se pintaron de gris. Este es el mapa definitivo con el que se construirá la matriz de adyacencias.

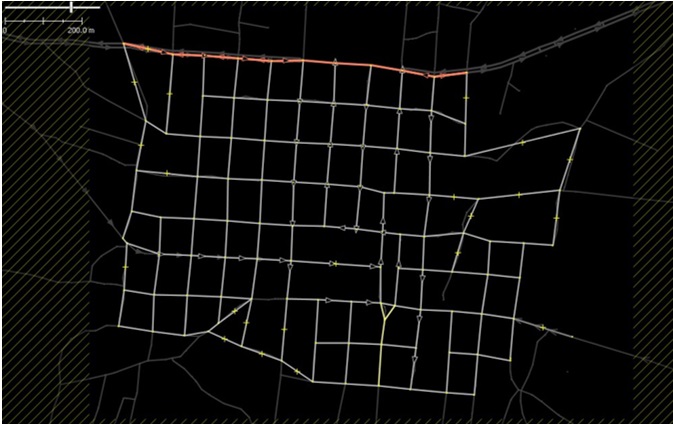Mapa después del proceso de limpieza; las calles sombreadas se eliminaron

Una vez que se obtiene el mapa definitivo sobre el que se va a trabajar, se construye la matriz de adyacencias que representará al grafo mixto. Como primer paso, se construyó un objeto de tipo JSON (Javascript Object Notation, por sus siglas en inglés) utilizando como llaves los identificadores de los nodos; a cada llave le corresponde un objeto que incluye sus adyacencias y su ubicación geográfica. Cada elemento de la lista de adyacencias incluye un identificador al nodo con el cual comparte un arco y la distancia asociada a dicho arco. A partir de este objeto, se puede iterar fácilmente para construir la matriz de adyacencias, la cual es necesaria para aplicar la técnica de optimización elegida.

8. Optimización

---

Una vez que se realizó la limpieza del mapa y se obtuvo un formato adecuado para trabajar, el siguiente paso es la aplicación de la técnica de optimización al problema en estudio. La técnica que se eligió está basada en la descripción del algoritmo de colonia de hormigas utilizado en el artículo “An Ant Colony Optimization for the Capacitated Arc Routing Problem” (Tsai and Ting, 2016), el cual cuenta con 6 etapas que serán descritas en la siguiente sección.

En la primera se inicializan los parámetros y se asigna el valor inicial de feromona a cada arco. El segundo paso consiste en la construcción de una solución factible al problema. Para construir una solución es necesario asignar un vehículo inicial y agregar arcos a su ruta, dichos arcos se seleccionan de acuerdo a una regla de transición. Una vez que ya se visitaron todos los arcos requeridos, se finaliza el proceso de construcción de solución. En caso de que el vehículo exceda su capacidad, se deja de añadir arcos a la ruta de este y se repite el proceso con un nuevo vehículo.

Una vez finalizada la construcción de una solución válida, se aplica la regla de actualización local con el fin de modificar los niveles de feromona (esta regla será descrita en el apartado de parámetros). En el momento en que todas las hormigas han concluido este proceso, inicia la etapa de búsqueda local. En este cuarto paso, los autores originales utilizan 3 técnicas de búsqueda local que son: intercambio, 2-óptimo e inserción

Sin embargo, para este trabajo solo se utilizará la técnica de 2-óptimo. Esta técnica fue propuesta por G. A. Croes (1958) y consiste en realizar intercambios en el orden en que se visitan los arcos para evaluar el nuevo costo; este proceso se realiza hasta que ya no se obtenga mejora alguna. Después de realizar el proceso de búsqueda local, se aplica la regla de actualización global de feromona que será descrita más adelante. Los pasos anteriores se realizan hasta que se complete el número total de iteraciones.

Para representar una solución se utiliza una lista de arcos los cuales están unidos de manera implícita por las distancias más cortas entre ellos. De este modo resulta sencillo realizar operaciones con las rutas como calcular su distancia total, actualizar feromona, entre otras. Para distinguir las rutas entre un vehículo y otro, se utiliza el símbolo 0. Para ejemplificar esto se muestra la Figura 5 que representa una solución de 3 vehículos para 8 arcos. El primer vehículo cubrirá en su ruta a los arcos 5, 6 y 8. El segundo a los arcos 1 y 3, y, por último, el tercer vehículo cubrirá los arcos 2, 4 y 7.

Representación de solución

Para la ejecución del algoritmo se utilizarán tres funciones distintas: la función de transición, la actualización local de feromona y la actualización global de feromona. La función de transición tiene como objetivo seleccionar el siguiente arco para continuar la construcción de la solución. La actualización local de feromona la aplica cada hormiga inmediatamente después de recorrer la ruta más corta entre el arco i y j mientras construye una solución. Además de la actualización local de feromona, esta variante de ACO tiene una actualización global de feromona llevada a cabo por la mejor ruta local y global, esto con el fin de balancear la explotación de la mejor ruta obtenida por las hormigas y la exploración de nuevas rutas para encontrar una mejor.

La búsqueda local es un proceso utilizado para mejorar la calidad de una solución. Existen varios tipos de búsqueda local; en este trabajo se va a utilizar la técnica de 2-optimo (2-opt, como se conoce comúnmente en inglés) la cual consiste en intercambiar el orden de visita de los arcos para evaluar si es más conveniente realizarlo de esa forma o de la manera original. Este proceso se repite hasta que ya no se encuentra una mejora y solo se va a llevar a cabo en la ruta de cada camión, es decir, el proceso sobre la ruta de un vehículo es independiente de los demás. El nombre de 2-opt procede de la idea detrás del algoritmo, que consiste en retirar 2 arcos de la ruta y sustituirlos por otros en búsqueda de una mejora. El algoritmo 1 describe el proceso realizado por la búsqueda local en cada ruta, también muestra la función 2optSwap, la cual, realiza el intercambio del orden en la ruta. La función calculaDistancia toma una ruta y calcula la distancia recorrida agregando el trayecto del depósito al inicio y del final al depósito. La función reverse toma una lista y la devuelve, invirtiendo el orden de sus entradas.

9. Resultados experimentales

---

En esta sección se presentan los resultados obtenidos con la metodología propuesta. Antes de aplicar la metodología propuesta en el problema real, se realizó primero una validación utilizando varios Benchmarks. Para esto se utilizaron dos de los benchmark más conocidos para el problema CARP. Los benchmark representan un conjunto de instancias del problema, los cuales, ya tienen una solución óptima conocida o un mínimo conocido, según sea el caso. La razón por la cual es importante el uso de un benchmark es para verificar el desempeño del algoritmo, brindando información sobre el comportamiento del mismo bajo ciertos parámetros. Para esto se utilizarán tres instancias del set de benchmark KSHS, que corresponden a las instancias 1, 2 y 6.

La solución óptima para cada uno de ellos es conocida, por lo que resultan ideales para comparar resultados con aquellos obtenidos por la técnica elegida; las distancias óptimas se muestran en la Tabla 1. Además, se realizará una prueba con la instancia egl-s4-C perteneciente al benchmark EGL, ya que el tamaño de esta instancia (140 vértices y 190 aristas) es más parecido al problema real. Cabe destacar que no se conoce la solución óptima de la última instancia; sin embargo, se tiene un mínimo conocido el cuál se utilizará como referencia para el análisis de los resultados.

Tabla 1
Soluciones óptimas por instancia

Para realizar la verificación se realizaron distintas configuraciones de parámetros (β, ρ, número de hormigas e iteraciones); por cada configuración se ejecutó el algoritmo 30 veces para las instancias de KSHS. Una vez que se obtuvieron los resultados, se elige la mejor configuración para utilizarla en la instancia perteneciente al benchmark EGL y se ejecuta el algoritmo 30 veces (solo se utilizó una configuración debido a la magnitud de la instancia), esto con el fin de obtener una muestra de buen tamaño para realizar un análisis de los resultados. Los valores propuestos para cada parámetro se presentan en la Tabla 2.

Tabla 2
Valores propuestos por parámetro

Tomando en cuenta las restricciones anteriores y utilizando la configuración obtenida gracias a los benchmarks, se procedió a evaluar la propuesta con el problema real.

10. Resultados usando los diferentes Benchmark

---

Después de realizar las ejecuciones de las tres instancias antes mencionadas se registraron los resultados para cada una de las 144 configuraciones; debido a la gran cantidad de resultados, únicamente se registraron las veinte mejores ejecuciones por configuración en una tabla. Los valores que se tabularon son el mínimo, máximo, promedio y desviación estándar de las soluciones obtenidas en la ejecución correspondiente. Además, se anexa la gráfica de la evolución de la solución para la mejor ejecución y, por último, se muestran las gráficas con las mejores soluciones por configuración de parámetros que resulten significativas para el análisis de los resultados sobre el benchmark.

El benchmark KSHS1 es la instancia más pequeña del set KSHS ya que solo cuenta con 8 vértices y 15 aristas. La restricción de capacidad por vehículo para esta instancia es de 150, la distancia total de todas las aristas es de 14661 y se requieren 4 vehículos para resolver este problema.

Las veinte mejores configuraciones, de acuerdo a la calidad de las soluciones obtenida en ellas se presentan en la Tabla 3.

Tabla 3

Resultados por configuración en la instancia kshs1

En la Tabla 3 se puede apreciar que el óptimo fue alcanzado en 17 configuraciones distintas (11.8 % del total de configuraciones), y se aprecia que la configuración 6 presenta la menor desviación estándar y promedio de todas, esto indica que además de lograr alcanzar el óptimo, tuvo el mejor comportamiento en cuanto a la calidad de soluciones encontradas. Al comparar con la siguiente mejor configuración (configuración 3), se puede observar que a pesar de que ρ disminuyo en 0.1, se obtuvo prácticamente el mismo comportamiento. Sin embargo, se observa que, al disminuir el número de hormigas, las soluciones comienzan a tener más distancia entre ellas, afectando al promedio y, por ende, a la desviación. Esto es debido a que, al reducir el número de hormigas, estamos limitando la capacidad de exploración del algoritmo en el grafo.

En general, las mejores configuraciones tienen un valor para β de 3 y ρ de 0.3, pero dependen enormemente del número de hormigas no solo para encontrar una buena solución, sino para que el promedio de las soluciones disminuya y así obtener soluciones de una mejor calidad. En la Figura 6, se muestra la evolución de la mejor ejecución obtenida para la configuración 6. En ella se puede observar que en las primeras iteraciones de la ejecución es cuando la distancia obtenida disminuye de manera precipitada y alcanza un punto donde ya no se obtiene una mejora hasta varias iteraciones después, siendo la iteración 275 cuando se obtiene la distancia óptima de 14661.

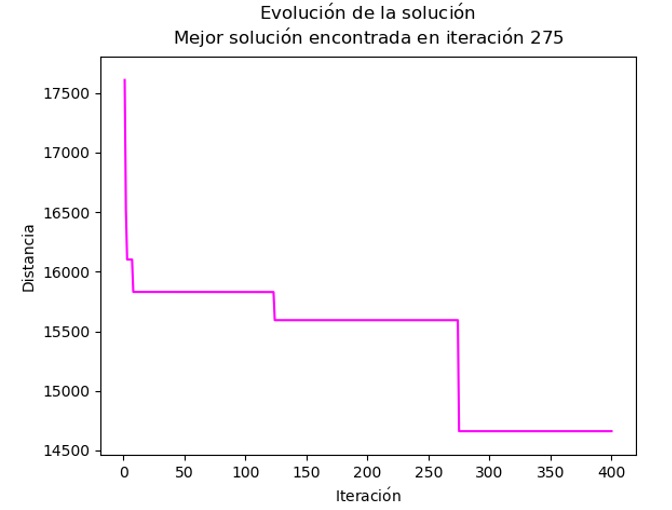Evolución de la mejor solución para la configuración 6

El benchmark KSHS2 cuenta con 10 vértices y 15 aristas. La restricción de capacidad por vehículo para esta instancia es de 150. La distancia total de todas las aristas es de 9863 y se requieren 4 vehículos para resolver este problema. Las veinte mejores configuraciones, de acuerdo a la distancia mínima obtenida en ellas se presentan en la Tabla 4.

A diferencia de la instancia anterior, el óptimo solo fue alcanzado en 3 configuraciones distintas (2.08 % del total de configuraciones). Tal y como se observa en la tabla, la configuración 2 obtuvo la distancia óptima, sin embargo, la configuración 9 obtuvo la mejor desviación estándar. Todas las configuraciones que lograron obtener el óptimo utilizaron un valor de β = 3 y 100 hormigas. Por otro lado, la configuración 9 tuvo un muy buen desempeño aún sin haber conseguido la distancia óptima (tan solo por una diferencia de 60), obtuvo el mínimo de los máximos y el promedio de las soluciones es el segundo mejor, por lo que también se considera una buena configuración.

Tabla 4

Resultados por configuración en la instancia kshs2

En la Figura 7, se muestra la evolución de la mejor ejecución encontrada por la configuración 2 ya que obtuvo el resultado óptimo y, además, presenta la menor desviación estándar. Esta ejecución encontró el resultado óptimo en la iteración 39 y solo hubo 2 variaciones en su evolución.

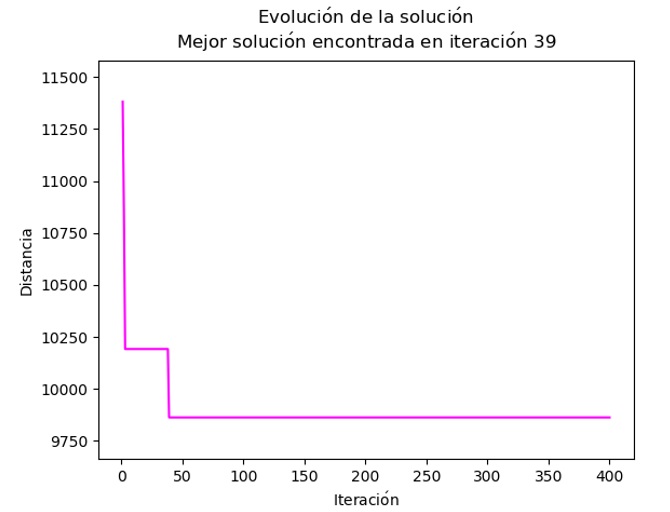Evolución de la mejor solución en la configuración 2

La instancia del benchmark KSHS6 cuenta con 9 vértices y 15 aristas. La restricción de capacidad por vehículo para esta instancia es de 150. La distancia total de todas las aristas es de 10197 y se requieren 3 vehículos para resolver este problema. Las veinte mejores configuraciones, de acuerdo a la distancia mínima obtenida en ellas se presentan en la Tabla 5.

Tabla 5

Resultados por configuración en la instancia kshs6

En esta instancia, el óptimo solo fue alcanzado en la configuración 1 (0.69 % del total de configuraciones) y, además, se tuvo el menor rendimiento del algoritmo. La segunda mejor solución está 100 unidades por encima del óptimo y se obtuvo en 11 configuraciones distintas. El mejor promedio de todas corresponde a la configuración 1 pero la mejor desviación estándar fue para la configuración 12, cuyo promedio es el noveno mejor. Nuevamente, el óptimo fue alcanzado con β = 3, ρ = 0.1, 100 hormigas y 400 iteraciones. En la Figura 8, se muestra la evolución de la mejor solución de la configuración 1 y la iteración en la que fue encontrado el óptimo.

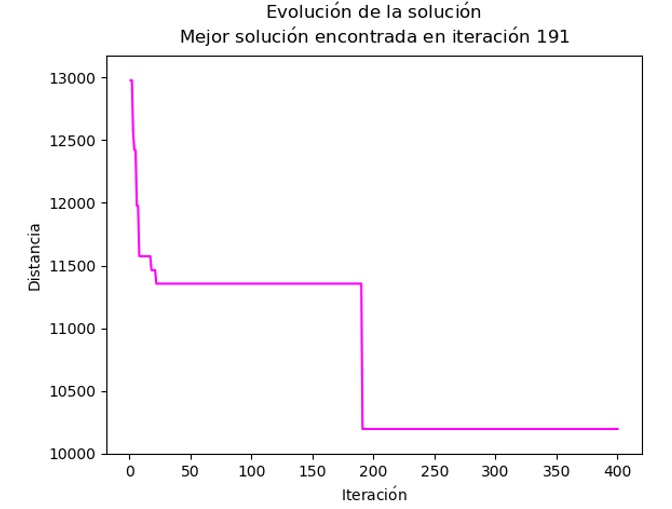Evolución de la solución para la mejor configuración

A partir de los resultados anteriores, se observa que la mejor configuración es β = 3, ρ = 0.1, 100 hormigas y 400 iteraciones. Esta configuración fue utilizada en la instancia de egl-s4-C, que cuenta con 140 vértices y 280 aristas; el mínimo conocido para esta instancia es de 20179 [min]. En la Tabla 6 se observa los mínimos reportados por otros autores y en la Tabla 7 se puede apreciar el mínimo, máximo, promedio y desviación estándar obtenidos al utilizar la configuración elegida.

Tabla 6

Mínimos reportados para la instancia egl-s4-C

Tabla 7

Resultados en la instancia egl-s4-C

En esta instancia no se logra alcanzar el óptimo en ninguna ejecución. A pesar de que la configuración elegida fue la mejor en el caso de las instancias KSHS, en este caso no tuvo un desempeño similar, esto en gran medida por el aumento tan repentino del espacio de búsqueda y por el número de iteraciones tan reducido para este espacio. Sin embargo, los resultados obtenidos si se acercaron a los reportados en la literatura, por lo que se puede decir que el algoritmo funciona adecuadamente. La evolución de la solución en la ejecución que obtuvo la menor distancia se muestra en la Figura 9.

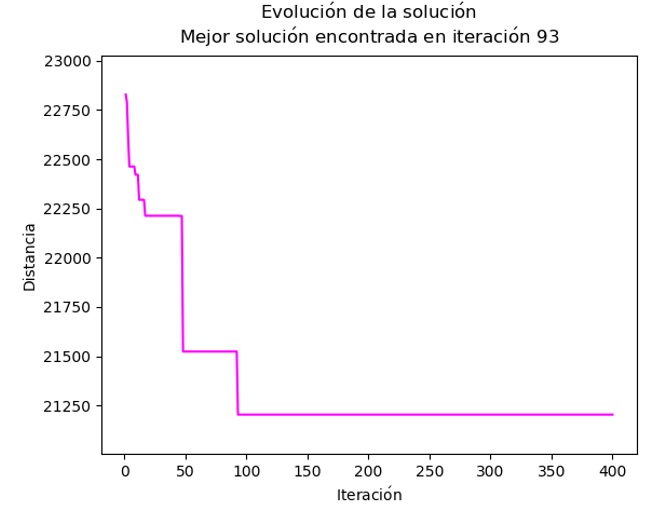Evolución de la solución para la mejor configuración

En todas las instancias del benchmark KSHS, se obtuvo el óptimo cuando se tenían los siguientes valores: β = 3, ρ = 0.1 y 100 hormigas. En la instancia 1, fueron necesarias 400 iteraciones para obtener el resultado óptimo, y en las otras dos, bastaron 100 iteraciones para encontrarlo. Debido a que el mejor valor de β es dependiente de la técnica y del problema, no se puede asegurar que el obtenido en estos experimentos sea el valor ideal; en este trabajo se utilizaron los valores propuestos en la literatura. Por otro lado, ρ sí tiene un efecto conocido ya que altera la evaporación de la feromona. En este trabajo, los mejores resultados se obtuvieron con el valor de ρ antes mencionado; otras configuraciones donde se obtuvo el óptimo y con un valor distinto de ρ presentan una mayor desviación estándar, lo que equivale a un comportamiento menos ordenado por parte de las hormigas, esto debido a que la evaporación de la feromona fue más rápida y, por ende, hubo menos convergencia hacia una misma solución, ocasionando una mayor exploración.

En el caso de la instancia egl-s4-C, los resultados fueron buenos, aunque, debido a que el espacio de búsqueda de la instancia es muy grande en comparación a las otras instancias, probablemente al incrementar el número de iteraciones y/o de hormigas mejoraría la calidad de las soluciones, acercándose aún más a los resultados reportados por otros autores.

Los autores originales de la técnica en la que se basó el algoritmo presentado utilizan 3 técnicas de búsqueda local en conjunto, hecho por el cual las soluciones que obtienen resultan muy buenas en tan pocas iteraciones, reportando que 150 iteraciones son suficientes para resolver los benchmarks. Por otro lado, el algoritmo que se presenta en este trabajo más sencillo y requiere de 400 iteraciones (quizá más) para obtener buenos resultados debido a que solo considera una técnica de búsqueda local, por lo que se debe nivelar esa falta de mejora continua en las soluciones encontradas con una mayor exploración del espacio de búsqueda.

Como conclusión final, el algoritmo propuesto puede atacar sin problema instancias del CARP, aunque será necesario la experimentación sobre cada instancia si se desea obtener una configuración paramétrica ideal para cada una.

11. Resultados usando en Milpa Alta

---

A partir de los resultados obtenidos en la sección de benchmarks, se eligió una configuración de parámetros que demostró su eficacia en todas las instancias en las que se probó. Dicha configuración será utilizada para la aplicación de la técnica de optimización al problema de recolección de basura en la colonia Villa Milpa Alta. Se realizarán 30 ejecuciones utilizando la configuración β = 3, ρ = 0.1 y 100 hormigas; cada ejecución contará con 400 iteraciones debido a la dimensión del problema. Por cada ejecución, se guardará el mejor resultado obtenido y una vez concluidas todas las iteraciones, se obtendrá el mínimo, máximo, promedio y desviación estándar de dichos valores, esto con el fin de centrar la atención en las mejores soluciones encontradas.

Además, se considerarán las siguientes restricciones durante la aplicación de la metodología propuesta:

1. Los arcos preservan el sentido original de las calles, es decir, importa el orden en el que se recorran los vértices.
2. Como consecuencia de la regla anterior, una calle de doble sentido se convierte en dos calles, cada una con un sentido.
3. Existe un vértice utilizado como depósito, de él partirán todos los camiones; también será el destino de los mismos una vez que agoten su capacidad de carga. Este punto se ubicó lo más cercano posible a la estación de transferencia.
4. Todos los arcos deben ser visitados al menos una vez por alguno de los camiones recolectores.
5. El grafo se ajusta al mapa descargado, por lo que pueden existir diferencias con el estado actual de las calles de Villa Milpa Alta.
6. El cálculo de la basura generada diariamente en la región se obtuvo a partir de la cantidad de residuos por persona al día en la alcaldía Milpa Alta, multiplicada por el número de habitantes de la colonia.
7. La cantidad de basura obtenida en el punto anterior se distribuyó de manera uniforme sobre la distancia, esto con el fin de asignar una cierta cantidad de residuos a cada arco.
8. El número de camiones a utilizar es de tres, esto debido a los cálculos realizados para encontrar la cantidad de basura producida diariamente en la zona.
9. La capacidad de carga de los camiones se fijó en seis toneladas.
10. No se cuenta con las rutas actuales que se utilizan para la recolección de residuos, este trabajo presentará una propuesta.

Tomando en cuenta las restricciones anteriores y utilizando la configuración obtenida gracias a los benchmarks, se obtuvieron los resultados de la Figura 10. Cabe destacar que la distancia obtenida es la suma de las distancias recorridas por cada camión, incluyendo salida y regreso al depósito.

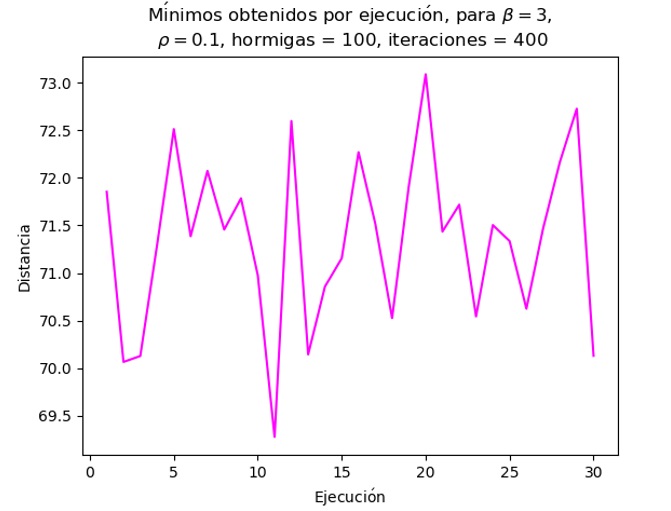Mejores resultados por ejecución para el problema de Villa Milpa Alta

Los resultados exactos obtenidos después de ejecutar el algoritmo (truncados a tres decimales) se muestran en la Tabla 9, mientras que en la Tabla 8 se muestra el máximo, promedio y desviación estándar de los mejores resultados.

Se observa que los resultados arrojan distancias de entre 69 y 73 km por lo que la máxima diferencia encontrada entre ellas es de 4 km aproximadamente, esto demuestra que el algoritmo tuvo un comportamiento similar en todas las ejecuciones.

La mayoría de los resultados obtenidos se encontró en la franja de 70.5 a 72.5 km, lo que puede indicar que debajo de esa distancia empieza a ser más difícil encontrar una solución y/o que el algoritmo se estancó en esa región. Sin embargo, se obtuvo un resultado de 69.27 km en la iteración 100 de la ejecución 11; en la gráfica se identifica de manera sencilla pues es el pico que se encuentra en la parte más baja.

Este mejor resultado no está tan alejado del promedio de soluciones obtenidas por el algoritmo, sin embargo, es el único que se encontró por debajo de los 70 km. La desviación estándar obtenida indica que la configuración utilizada hace que el comportamiento de las soluciones sea estable, esto es bueno ya que se pueden esperar soluciones dentro del mismo rango y además hace notar el trabajo de la colonia de hormigas, alejándose de un comportamiento al estilo de búsqueda aleatoria.

Con respecto a la evolución de la solución durante el proceso del algoritmo, el mejor resultado se obtuvo en la iteración 100 de la ejecución correspondiente; de la iteración 1 a la 100 tuvo un muy buen desempeño pues mejoró en varias ocasiones la calidad de la solución. El hecho de que no haya podido mejorar la solución en 300 iteraciones más puede ser por varias razones, entre ellas las más probables son: la exploración que realizaron las hormigas no fue exhaustiva o se encontró un mínimo local (incluso la solución óptima). Este comportamiento se puede apreciar en la Figura 11.

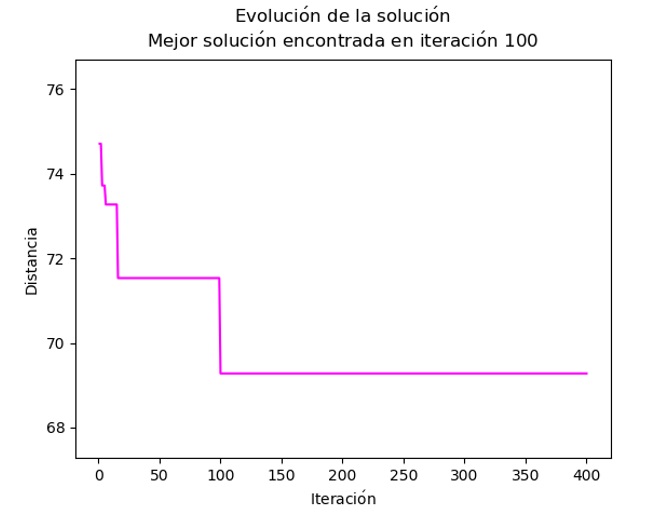Evolución de la solución en el problema de Villa Milpa Alta

Debido a la complejidad del problema, no se cuenta con un medio para decir que las so- luciones encontradas son buenas o malas, mucho menos se puede hablar de un óptimo ya que sería necesario obtener todas las soluciones posibles para poderlas comparar entre sí. Debido a que las rutas de recolección no se proporcionaron, no es posible realizar una comparación con los resultados descritos anteriormente, y las rutas actualmente en uso.

Tabla 8

Datos estadísticos de los resultados obtenidos

Tabla 9

Mejores resultados por ejecución para el problema de Villa Milpa Alta

Dentro de la mejor solución obtenida también se analiza la distancia a recorrer por cada camión. En este caso se obtuvieron los siguientes valores: 25.949, 26.481 y 16.486 km. Para mostrar las rutas generadas, se graficó el mapa de la colonia Villa Milpa Alta y se dibujó la ruta sobre sus calles; cada calle está representada por una flecha de color negro que indica el sentido de circulación, las flechas azules y rojas pertenecen al recorrido del camión, el color rojo indica que se realizó el servicio de recolección en esa calle y el color azul indica que el camión transitó por esa calle, pero no recogió basura. El depósito se encuentra en la parte inferior derecha de cada imagen y corresponde al vértice 107.

Es interesante observar que el algoritmo dividió el mapa en dos partes, ya que la primera ruta brinda el servicio de recolección en la zona norte y oeste principal- mente, mientras que la segunda ruta da servicio a la parte sur y este, la última ruta solo cubre algunas calles a las cuales no se les dio servicio en las rutas anteriores, enfocándose principalmente en la zona noreste del mapa. Las primeras dos rutas recorren casi la misma distancia mientras que la tercera solo es para terminar el trabajo que no pudieron hacer las otras, este comportamiento se observa en las Figuras 12, 13 y 14. Otro punto importante al analizar las figuras es que los camiones no dan servicio en algunas calles, esto resulta poco intuitivo de primera mano ya que la mayoría de las personas optaría por una estrategia glotona o greedy (recogiendo basura por todas las calles que transite hasta llenar su capacidad) al momento de crear rutas de recolección. Esto también tiene un impacto en la implementación de este trabajo en la vida real ya que los habitantes tendrían que identificar de algún modo el camión que les corresponde.

La forma en la que se construyó el algoritmo y en que se codificó el grafo no permiten que se agreguen camiones adicionales a las soluciones, ya que se trabaja con el número de camiones justo para la cantidad de residuos que genera la colonia. En caso de que se quisiera utilizar un número menor de camiones, uno o varios de ellos tendrían que cubrir más de una ruta. Además de esto, el hecho de considerar las calles de doble sentido como dos arcos con direcciones opuestas hace que en algunos momentos el algoritmo opte por hacer una vuelta en “U”, lo que sería poco viable en el problema real. Se necesitan más datos sobre el mapa y restricciones sobre el grafo para lograr evitar al 100 % este tipo de comportamientos.

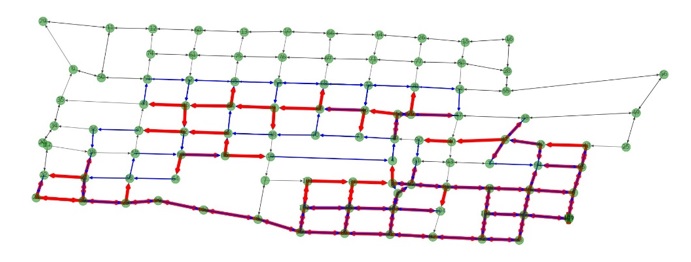Primera ruta generada

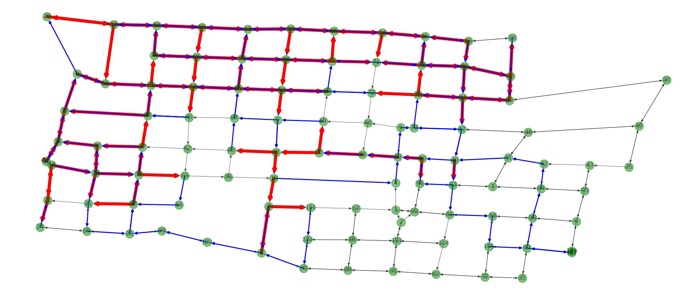Segunda ruta generada

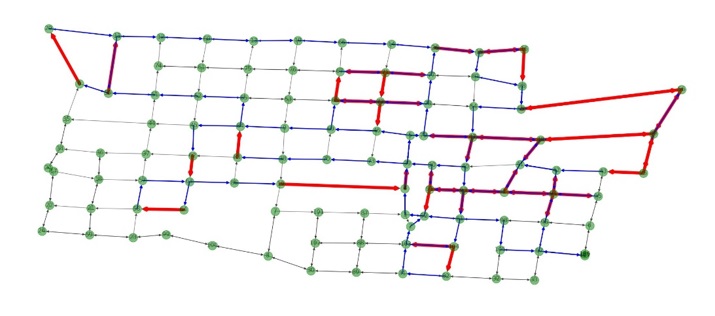Tercera ruta generada

12. Conclusiones

---

La problemática de la recolección de residuos en la Ciudad de México aumenta año con año, esto hace que cada vez sea más difícil encontrar soluciones factibles que se puedan llevar a cabo para atacar de manera efectiva el problema. Uno de los puntos clave en la recolección es la generación de rutas, las cuales se siguen obteniendo a través del criterio y experiencia de los operadores de los vehículos de recolección. Este trabajo tuvo como uno de sus objetivos presentar una propuesta para optimizar la creación de rutas de recolección tomando como caso de estudio la colonia Villa Milpa Alta, de la alcaldía que lleva el mismo nombre.

En el proceso de optimización de rutas de recolección, la obtención del grafo para aplicar la técnica de optimización tuvo varias dificultades y limitaciones. En primer lugar, no existe una plataforma gubernamental para descargar los datos actualizados de la zona geográfica sobre la cual se desarrolló el tema, por lo que, se tuvo que recurrir a otras alternativas que presentaban algunos datos erróneos, incompletos y desactualizados. Otra dificultad fue que una vez que se obtuvieron los datos fue necesario ajustarlos a las necesidades del caso de estudio. Este proceso tomó mucho tiempo debido a que se tenía que corroborar los datos calle por calle, con el fin de que el grafo estuviera lo más apegado a la realidad como fuera posible.

A pesar de la gran cantidad de artículos referentes al problema CARP, pocos son los que explican de una manera detallada la implantación de la técnica y el procedimiento que siguieron para resolver su problema. Además, la dificultad del problema CARP hace que muchas de las técnicas utilizadas por otros autores fueran muy complejas de implementar. La elección de la variante de ACO utilizada en este trabajo se debió a que era la única que no solo mostraba buenos resultados en problemas similares al de este trabajo, sino que, además, la claridad de su explicación facilitó la puesta en práctica.

Al observar los resultados de los benchmarks se comprobó la calidad de la técnica elegida y se encontró una configuración que funcionó de buena manera en el problema real. En especial la instancia egl-s4-C fue de gran ayuda ya que sus dimensiones eran similares a las del problema a resolver y, a pesar de no tener una solución óptima registrada, tenía varios resultados obtenidos por otros autores, los cuales no estuvieron tan alejados de los valores que se obtuvieron con este programa.

Para poder comparar de manera adecuada los resultados obtenidos en el problema real sería necesario contar con las rutas utilizadas actualmente en la colonia Villa Milpa Alta. Sin embargo, la alcaldía no brindó la información requerida, por lo que no fue posible comparar las rutas obtenidas con las actuales.

Con respecto a las configuraciones, sería adecuado realizar distintas variaciones de parámetros, tal y como se hizo en los benchmarks, para obtener un conjunto de resultados y poderlos analizar y comparar entre sí, con el fin de observar la influencia de cada parámetro en la calidad de la solución. Esto también ayudaría a determinar si existe alguna configuración que brinde un mejor desempeño en este problema, ya que es importante recordar que no existe una mejor configuración para todos los problemas, sino que el desempeño de cada una depende del mismo. En problemas de gran magnitud, como el del presente trabajo, se requiere de mucho tiempo y poder computacional para probar varias configuraciones, siendo esto una enorme limitante para realizar las comparaciones antes mencionadas.

La metodología propuesta es tan flexible y general que podría extender sin problema a toda la Ciudad de México. Aunque el espacio de búsqueda crecería considerablemente, el uso de un equipo de cómputo más poderoso, podría ayudar en la ejecución de los algoritmos propuestos de forma rápida. Como trabajo futuro, se está considerando la paralelización del algoritmo para encontrar las rutas óptimas en un tiempo menor. Sin embargo, el método de recolección de basura actual, no permite aplicar técnicas de optimización de una manera sencilla, ya que obliga a tomar en cuenta casi todas las calles de una determinada región. En otros trabajos se hace hincapié en la reducción del espacio del problema debido al punto antes mencionado; para poder hacer algo similar en la ciudad de México sería necesario realizar algunos cambios al sistema actual de recolección. Uno de ellos podría ser establecer horarios fijos de servicio a ciertas calles, esto provocaría que el problema se reduzca solo a las calles a las que se dará servicio y no a toda la colonia, reduciendo la complejidad. Otra propuesta sería el uso de contenedores donde las personas depositen su basura, así, los camiones solo tendrían que pasar a los contenedores en vez de recorrer todas las calles. También se podrían establecer regiones geográficas dentro del área a la que se dará servicio y asignar vehículos a cada zona, con el fin de aplicar la técnica de optimización a cada zona en vez de aplicarla a toda la región, convirtiendo cada zona en un subproblema del problema original, disminuyendo así su complejidad.

El proceso de cambiar el modelo de recolección actual por otro más eficiente, no será fácil ya que se necesitará nueva infraestructura y disposición por parte de la población para llevarlo a cabo. Sin embargo, esta propuesta muestra que la ciencia puede aplicarse a la solución de problemas complejos, los cuales se presentan cotidianamente en nuestras ciudades.

Referencias

• [min, ] Benchmarks. Accessed: 2018-09-01.
• Angelelli, E. and Speranza, M. G. (2002). The Application of a Vehicle Routing Model to a waste-collection problem: two case studies. Palgrave Macmillan Journals.
• Astolfi, A. (2006). Optimization, an introduction.
• Aynodkar, N. A. and Bhosale, S. M. (2015). Application of arc routing problem for municipal solid waste collection in Kolhapur city, India.
• Berge, C. (1970). Graphs. Elsevier Science Publishing Company.
• Chva´tal, V., Cook, W., Dantzig, G. B., Fulkerson, D. R., and Johnson, S. M. (2010). Solution of a Large-Scale Traveling-Salesman Problem Berlin: Springer Berlin Heidelberg. pp. 7–28
• Corbera´n, A. and Prins, C. (2010). Recent results on arc routing problems: An annotated bibliography. Networks, 56 (1):50–69.
• Croes, G. A. (1958). A method for solving traveling salesman problems.
• Dantzig, G. B. and Ramser, J. H. (1959). The truck dis-patching problem. Manage. Sci.
• Dorigo, M. (1992). Optimization, Learning and Natural Algorithms. Dipartimento di Elettronica.
• Dorigo, M. and Stu¨tzle, T. (2004). Ant Colony Optimization The MIT Press.
• Dror, M. (2000). Arc Routing - Theory, solutions and applications. Kluwer Academic Publishers.
• Eiselt, H. A., Gendreau, M., and Laporte, G. (1995). Arc Routing Problems Part II: The Rural Postman Problem. Operations Research.
• Fukasawa, R., Longo, H., Lysgaard, J., Araga˜o, M. P. d., Reis, M., Uchoa, E., and Werneck, R. F. (2006). Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Mathematical Programming, 106 (3):491–511.
• Ghiani, G. and Improta, G. (2000). An efficient transfor- mation of the generalized vehicle routing problem. European Journal of Operatio- nal Research, pp. 11–18
• Gobierno de la Ciudad de México (2016). Inventario de Residuos Sólidos de la Ciudad de Me´xico. Secretaría del Medio Ambiente de la Ciudad de Méico.
• Golden, B. L., Dearmon, J. S., and Baker, E. K. (1983). Computational experiments with algorithms for a class of routing problems. Computers and Operations Research, (10): pp. 47–59.
• Golden, B. L. and Wong, R. T. (1981). Capacitated arc routing problems. Networks, 11 (3):305–315.
• Goss, S., Aron, S., Deneubourg, J., and Pasteels, J. (1989a). Self- organized shortcuts in the Argentine ant. Naturwissenschaften, 76 O(12):579–581
• Goss, S., Aron, S., Deneubourg, J. L., and Pasteels, J. M. (1989b). Self-organized shortcuts in the Argentine ant. Naturwissenschaften
• Grimaldi, R. P. (1998). Matemáticas discreta y combinatoria: una introducción con aplicaciones. México, Addison Wesley Longman.
• Holland, J. H. (1992). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. USA: MIT Press.
• Ismail, Z. and Loh, S. L. (2009). Ant colony optimization for solving solid waste collection scheduling problems. (5): 199–205.
• Johnson, M. R. G. D. S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness (Series of Books in the Mathematical Sciences). W. H. Freeman
• K., M. (1932). Das Botenproblem, in: Ergebmisse eines Mathematischen Kolloquiums 2.
• Koza, J. R. (1992). Genetic Programming: On the Programming of Com- puters by Natural Selection. USA: MIT press.
• Kwan, M.-K. (1962). Graphic programming using odd or even points
• Lacomme, P., Prins, C., and Ramdane-Cherif, W. (2004a). Competitive memetic algorithms for arc routing problems. Annals of Operations Research, 131 O(1):159–185.
• Lacomme, P., Prins, C., and Tanguy, A. (2004b). First Competitive Ant Colony Scheme for the CARP. Berlin: Springer Berlin Heidelberg, pages 426–427
• Lenstra, J. K. and Kan, A. H. G. R. (1976). On general routing problems.Networks, 6 (3):273–280.
• Liu, J. and He, Y. (2012). Ant colony algorithm for waste collection vehicle arc routing problem with turn constraints. In 2012 Eighth International Conference on Computational Intelligence and Security, pages 35–39.
• Longo, H., Poggi de Aragao, M., and Eduardo, U. (2006). Solving capacitated arc routing problems using a transformation to the cvrp. Computers & Operations Research, (33), 1823–1837.
• Martello, S. and Toth, P. (1990). New York New York: John Wiley & Sons, Inc.
• Miiller-Merbach, H. (1983). Zweimal travelling salesman.
• Osman, I. H. and Laporte, G. (1996). Metaheuristics: A bibliography. Annals of Operations Research, 63 (5):511–623.
• Otoo, D., Amponsah, S. K., and Sebil, C. (2014). Capacitated Clustering and Collection of Solid Waste in Kwadaso Estate, Kumasi. Journal of Asian Scientific Research, 4 (8):460–472.
• Parkinson, A. R., Balling, R. J., and Hedengren, J. D. (2013). Optimization methods for engineering design. Applications and theory. Brigham Young University.
• Pemmaraju, S. and Skiena, P. S. (2003).Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. R. Cambridge University Press.
• Pereira, F. and Tavares, J. (2009)Bio-Inspired Algorithms for the Vehicle Routing Problem, 161 Springer, N/A, spr edition.
• Prins, C. (2009). A GRASP Evolutionary Local Search Hybrid for the Vehicle Routing Problem. Berlin: Springer Berlin Heidelberg, pages 35–53
• Rabbani, M. and Mohammadi, S. (2015). Modelling a multi depot k-chinese postman problem with consideration of priorities for servicing arcs. American Scientific Publishers.
• Rizzoli, A. E., Oliverio, F., Montemanni, R., and Gambardella, L. M. (2004).Ant colony optimisation for vehicle routing problems: from theory to applications. Technical report.
• Russell, S. and Norvig, P. (2010). Artificial Intelligence A Modern Approach. Prentice Hall.
• Secretaría de Desarrollo Social (2001). Manual Te´cnico sobre generacio´n, recoleccio´n y transferencia de residuos so´lidos municipales. Gobierno Federal.
• Shan-Huen, H. and Tsan-Hwan, L. (2014). Using Ant Colony Optimization to solve Periodic Arc Routing Problem with Refill Points. Journal of Industrial and Production Engineering.
• Toth, P. and Vigo, D., editors (2001).The Vehicle Routing Problem. USA: Society for Industrial and Applied Mathematics.
• Tsai, H.-S. and Ting, C.J. (2016). An ant colony optimization for the capacitated arc routing problem.
• Ufuktepe, U. and Bacak Turan, G. (2005). Applications of graph coloring.
• Vidal, T. (2017).Node, edge, arc routing and turn penalties: Multiple problems—one neighborhood extension. (65).
• Vidal, T., Crainic, T. G., Gendreau, M., and Prins, C. (2014). A unified solution framework for multi-attribute vehicle routing problems. European Journal of Operational Research, 234 (3):658 – 673.
• Von F. Voigt, B. (1831). Das handlungsreisendenproblem, tsp.
• Wohlk, S. (2008). A decade of capacitated arc routing. Aarhus University.
• Xing, L. N., Rohlfshagen, P., Chen, Y. W., and Yao, X. (2011). A hybrid ant colony optimization algorithm for the extended capacitated arc routing problem. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 41 O(4):1110–1123.
• Xue, W. and Cao, K. (2016). Optimal routing for waste collection: a case study in Singapore. International Journal of Geographical Information Science, 30 (3):554–572.
• Yu, H. (2014). Optimization of Vehicle Routing and scheduling with travel time variability-application in winter road maintenance. Department of civil and environmental Engineering.