Introduction
Personnel selection aims to place the right people to the right place in a workplace. It is a sub-phase of an administrative process, and the selection is included in the "integration" phase. This activity is a set of tasks that follows a methodology of decision-making, the one determining if a worker could be hired or not. The hiring body must evaluate each candidate’s set of skills and experiences. The fulfillment of this objective faces different obstacles, e.g. the subjectivity of both the employer and the applicant. However, the personnel selection works with basic principle that it is the person who adapts to the job and not vice versa (Weihrich and Koontz, 2015). The process itself is not usually fully validated until an employee is hired. This selection is commonly considered as three-phase process (Figure 1).
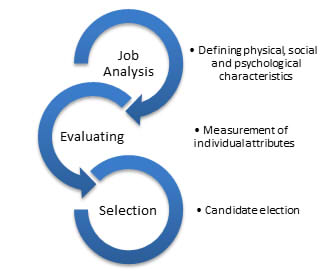 |
Personnel selection process (own elaboration) |
Figure 1. Personnel selection process (own elaboration)
The selection process can become complicated in large organizations where different areas work towards diverse set of objectives. What is more, organizations sometimes state ambiguous objectives and confusing goals, which are difficult or impossible to achieve. Ibarra Colado (1994) called these organizations as complex organizations. The selection of a personnel in complex organizations can become an extremely difficult task requiring additional instruments to analyze all candidates’ information. The growing importance attached to personnel selection process has paved the way for analytical decision-making approaches (Dursun and Karsak, 2010).
To facilitate this process, many organizations from various areas (Economics, Social Sciences, Medical Sciences) have started using personnel selection methods based on Multi-criteria Decision Analysis (MCDA) or Fuzzy logic. For example, the application of MCDA for the personnel selection can be found in Chen and Cheng (2005). The antecedent of this model can be found in Liang and Wang (1994) who proposed an algorithm and a diffuse classification method. Karsak (2001) used the concept of ideal and inferior solutions for the selection of the most appropriate candidate.
Sport team as a complex organization
A sport team is seen as a complex organization if we consider the following characteristics:
- Consists of several interconnected units (loose coupling), weakly cohesive and fragmented tasks (for example between technical management, medical service, finance, marketing, etc.).
- Strong ambiguity of preferences exists, having several contradictory objectives (for example contradictories between obtaining higher income, promoting the sport or providing a good show).
- Indeterminate technology, it is an immaterial process that does not clearly define inputs and outputs, team procedures, the integration of each player, individual performance, technique, etc.
- Fluid participation in the decision processes. Although there is a previously defined strategy at the moment of a game, players face specific situations that must be solved immediately. In this case, players enter or exit the decision-making processes. Similarly, made decision introduce new problems, as well as have a great capacity to influence the decisions of others.
Similarly, as the personnel selection in complex organizations, it is of a high importance to select the right player for the right position. In this case, MCDA methods are applied in a similar way, helping coaches (managers) to select the best possible candidate for a specific position or evaluate an importance of predefined attributes. For example, Ozceylan (2016) applied Analytic Hierarchy Process (AHP) to evaluate importance of football skills for players in Turkish league. Linear programming for the selection of the main team was then used. Huang, Lin and Hu (2015) applied AHP to determine the importance of the indicators of potential badminton players. Kamble et al. (2011) applied AHP for a selection of cricket players for batsmen, bowlers, all-rounders and wicket keeper positions. Boon and Sierksma (2003) employed linear programming model for optimal team selection in volleyball. Bhattacharjee and Saikia (2016) used binary integer programming for selecting players of a cricket team, whereas Ahmed, Deb and Jindal (2013) used multi-objective optimization and decision-making approaches for a similar purpose.
Further, two-stage optimization models can be applied for a team/player selection. Tavana et al. (2013) proposed a two-phase framework for player selection and team formation in football. In the first phase, the authors evaluated players with a fuzzy ranking method and selected top performers for inclusion in the team. In the second phase, alternative combinations of the selected players were evaluated with a Fuzzy Inference System (FIS) to select the best combinations for a team formation. Similarly, Qader et al. (2017) presented a methodology to assess and rank football players based on MCDA. In the first part, players are assessed using anthropometric test, fitness-related test and skills-related test. Then, Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) method is used to obtain the ranking of these players. Dadelo et al. (2014) developed integrated model of TOPSIS and expert judgement assessment and ranking (based on statistical data and subjective coaches’ evaluation) to ensure greater efficiency in the assessment, rating and selection of basketball players.
This article aims to propose personnel selection methods based on decision-making models for complex organizations characterized by situations of loose coupling, ambiguity or anarchists. We propose the use of a combination of AHP and TOPIS for a selection of the Mexican football team for the world cup Russia 2018.
The article is divided as follows: in the first part, the concept of complex organizations is exposed. In the second part, the proposed methodology for a sports organization is explained. In the third part the achieved results are presented, followed by a discussion over the main contributions of the work. We conclude the article with the final remarks and potential application of the proposed methodology.
Materials and Methods
Analytic Hierarchy Process (AHP)
Analytic Hierarchy Process was developed by Saaty (1977, 1980) and works with both qualitative and quantitative evaluation of preferences. To obtain criteria priorities, pairwise comparisons based on the fundamental verbal/numerical 1-9 scale is required (Table 7). The number of necessary comparisons for each comparison matrix is $ n ({n - 1})/2$ where $n$ is the number of criteria. Each criterion gains a geometric mean of its comparisons, which are then normalized.
An important requirement is to test consistency of our stated preferences, as human-made decisions can be mutually inconsistent because of the human nature. The most commonly used method for consistency check was developed by Saaty (1977), who proposed a consistency index (CI) related to eigenvalue method. CI is obtained as
|
\begin{equation}\text{CI} = \dfrac{\lambda_{max} - n}{n - 1} \end{equation} |
where &\lambda_{max}$ is the maximal eigenvalue of the pairwise comparison matrix. The consistency ratio (CR) is given by
|
\begin{equation}\text{CR} = \dfrac{\text{CI}}{\text{RI}} \end{equation} |
where RI is the random index obtained in Table 1.
 |
AHP - Random indices (Saaty, 1977) |
The priorities are considered consistent if the consistency ration is less than 10%. SuperDecisions software is used to count the criteria preferences and to test consistency of the preferences. The AHP method is used to count priorities of players attributes based on expert evaluation.
Technique of Order Preference Similarity to the Ideal Solution (TOPSIS)
The fundamental idea of TOPSIS is that the best solution is the one, which has the shortest distance from the ideal solution, and vice versa the farthest distance from the inferior solution. (Ishizaka and Nemery, 2013) The performances of $n$ alternatives $a$ with respect to $m$ criteria $i$ are collected in decision matrix $X = (x_{ij})$, where $i=1, 2, ... , m$ and $j=1, 2, ..., n$. First, the performances of different criteria are normalized in order to be able to compare the measure of different units. Using the distributive normalization, we get
|
\begin{equation} r_{ij}\dfrac{x_{ij}}{\sqrt{\sum_{j=1}^nx^{2}_{ij}}} \text{ for i}=1, 2, ..., m \text{ and j} = 1, 2, ..., n. \end{equation} |
The normalized performances $r_{ij}$ are weighted with its corresponding weight $w_{i}$ to get weighted normalized decision matrix as
|
\begin{equation} v_{ij}=w_{i} \cdot r_{ij} \end{equation} |
Using the weighted normalized performances, we identify ideal and inferior alternatives considering the best and worst virtual performances. For the ideal alternative as
|
\begin{equation} a^{+}=(v^{+}_{i},...,v^{+}_{m}) \end{equation} |
and for the inferior alternative as
|
\begin{equation} a^{-}=(v^{-}_{i},...,v^{-}_{m}) \end{equation} |
where $v^{+}_{i}= \text{max}(v_{ij})$ if the criterion $i$ is to be maximized and $v^{-}_{i}= \text{min}(v_{ij})$ if the criterion $i$ is to be minimized.
To count the distance of each alternative from the ideal alternative, we get
|
\begin{equation} d^{+}_{i}= \sqrt{\displaystyle\sum_{i}(v^{+}_{i}-v_{ij})^{2}},i=1,2,...,m \end{equation} |
and the distance from the inferior alternative as
|
\begin{equation} d^{-}_{i}= \sqrt{\displaystyle\sum_{i}(v^{-}_{i}-v_{ij})^{2}},i=1,2,...,m \end{equation} |
The closeness coefficient of each alternative to the ideal solution is obtained as
|
\begin{equation} C_{i}=\dfrac{d^{-}_{i}}{d^{+}_{i}+d^{-}_{i}} \end{equation} |
The closeness coefficient is always between 0 and 1, where 1 refers to the ideal (preferred) solution.
The TOPSIS method is used to count the closeness coefficients of all players to identify the ideal players for team selection.
Data
In the analysis, we use data based on EA Sports players’ evaluation, which is publicly available online (SoFIFA, 2017). EA Sports uses help of 300 data editors and feedback from 9,000 data reviewers, which is combined to create 300 different data fields and 35 distinct attributes. These are then synthesized to create an individual player’s overall rating. The whole database includes around 18,000 players from leagues around the world.
For the purpose of the analysis, we have constructed two different databases of the top 150 Mexican players evaluated by SoFIFA. The first database includes the top 150 players and their evaluation linked to August 2013. This information is used to validate the proposed methodology. The second database includes the top 150 players linked to August 2017. This information is used for the selection of the Mexican team for the 2018 FIFA World Cup in Russia. Both databases include complete players’ evaluation based on 32 distinguish attributes (Table 8). The selection of the players did not consider proportional balance between positions (goalkeeper, defense, midfielder and forwards) as most of the players are able to play in multiple positions. However, the balance of players is sufficient for the calculation (Table 2).
Selection of attributes and their importance
Mexican national team has been using different formations during their last games depending the opponents and home/away games (4-3-3, 4-5-1, 4-4-2 and 5-3-2). However, and for the purpose of this analysis, we consider seven basic positions no matter of the selected formation (Figure 2). In this scheme, #1 refers to goalkeeper (GK), #2 to central back (CB), #3 to left back (LB) and right back (RB), #4 to central defensive midfielder (CDM, CM), #5 to central attacking midfielder (CAM, CM), #6 to left midfielder/wing (LM, LW) and right midfielder/wing (RM, RW) and #7 to forward/striker (ST, CF). Seven basic positions can be considered as the abilities/skills for LB and RB are basically the same, similarly in case of LM and RM. In some cases, positions #4 and #5 can be considered as one (see e.g. Ozceylan, 2016). However, we see significant differences between a defensive and offensive midfielder. In the other formation, the main difference holds in number of players in each position.
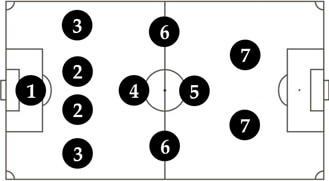 |
Basic positions for 4-4-2 formation. |
Figure 2.Basic positions for 4-4-2 formation
Table 2 summarizes the distribution of the pre-selected players in each database regarding the seven basic positions. As most of the players are able to play in multiple positions, the sum does not hold 150 players. In accordance to the official FIFA regulations (FIFA, 2017), each qualified team can nominate 23 players in total, from those 3 must be goalkeepers. The Mexican selection for the 2006 FIFA World Cup included 3 goalkeepers, 9 defenders, 5 midfielders and 6 forwards, for the 2010 FIFA World Cup 3 goalkeepers, 8 defenders, 4 midfielders and 8 forwards, whereas for the 2014 FIFA World Cup the team included 3 goalkeepers, 9 defenders, 6 midfielders and 5 strikers (not considering multiple positions). Take this into account, we seek to select 3 goalkeepers, 9 defenders, 6 midfielders and 5 forwards. More precise, we seek to select 3 goalkeepers, 5 central backs, 2 left backs, 2 right backs, 2 central defensive midfielders, 2 central attacking midfielders, 1 left midfielder, 1 right midfielder and 5 forwards for the 2018 FIFA World Cup selection.
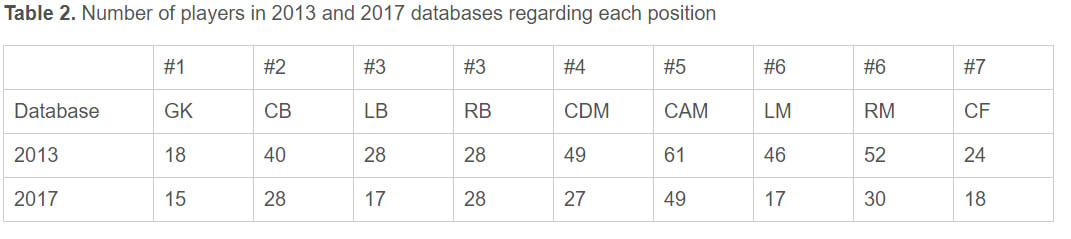 |
Number of players in 2013 and 2017 databases regarding each position. |
As 32 different attributes exist for each player (Table 8) the players’ evaluation and selection would be too difficult. Therefore, we limit the evaluation to only eight most important attributes to each position. The selection of the eight most important attributes requires a qualitative perspective and recognizes a necessary subjective approach, for which we request experts’ opinion. The team of experts included: Hugo Salcedo (international football analyst), Eduardo Bacas (Argentinian ex-football player and football analyst), Damián Zamogilny (Argentinian ex-football player and football analyst), Cecilio de los Santos (Uruguayan ex-football player and football analyst) and Raúl Sarmiento (football commentator). All these experts work in division of Mexican television network Televisa.
Prior to the interview, we prepare cards for each desirable attribute of a player, in total 32 cards, on the obverse with the name of an attribute and on the back a basic explanation in Spanish (Table 8). Attributes represent qualitative linguistic categories. The task of the experts was to select eight attributes by position. The experts were interviewed separately, so one's answers did not influence those of another expert. The attributes can be repeated for all positions without restrictions. In addition, we asked each expert to evaluate the importance of the criteria selected using the AHP scale (Table 7). We use SuperDecisions to tell the importance of the attributes for each position. The consistency index of all evaluations varied between 0% and 2.7% (with an average of .485% and SD .52), that is, significantly lower than the consistency level of 10%
As expected, the experts’ selection of the attributes was not unanimous. Therefore, to get the eight most important attributes for each position, we have counted global weighted importance for each position. The global weighted importance was obtained as an average from the individual experts’ evaluations multiplied by the number of occurrences of a particular attribute among all experts. We than normalized the global weighted importance to obtain the total importance equal to 100%. In this way we convert linguistic labels, of qualitative order, into values of a quantitative order.
Table 3 shows the selection of all attributes.
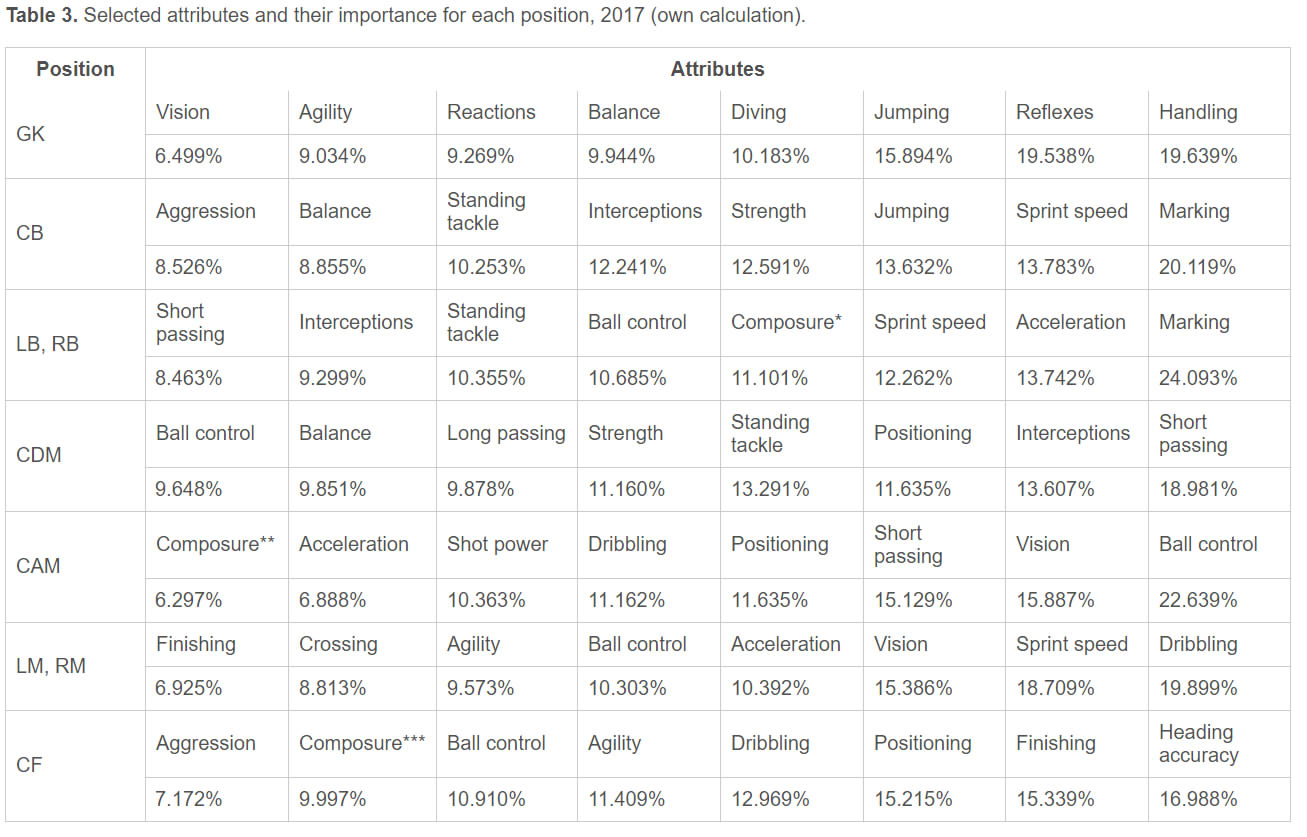 |
Selected attributes and their importance for each position, 2017 (own calculation). |
Model validation
Before selecting the Mexican football team for the 2018 World Cup in Russia, we have evaluated the methodology using ex post data. Using the selected attributes for each position along with SoFIFA data from August 2013, we have selected Mexican football team for the 2014 World Cup in Brazil. Table 4 compares the result of the selection with the World Cup team based on the results from TOPSIS. In case of the World Cup team, we do not distinguish the seven basic positions, as we do in case of the Selected team. The methodology used for the selection proposed 13 same players out of 23 players (56.52% accordance). Although the accordance of both selections is a bit under 60%, the methodology has proved its usability and applicability. The selection has been made based on the experts’ perception of the most important attributes for each position in 2017, i.e. four years later the original selection.
Table 4 also shows the distance from the ideal player for each position and the ranking. For example, Jonathan Orozco was selected as the best goalkeeper with score .7636, i.e. his distance is 23.64% to the ideal combination of all goalkeepers’ skills in the sample. In some cases, some players were selected as ideal candidates to more positions at the same time. This happened due to the universality of some players. In this case, we kept a player for a position with the higher overall score. For example, Carlos Salcido was selected for LB position (.8345), CB (.7099) and CDM (.7733). We kept Carlos Salcido for the LB position due to the shortest distance to the ideal case. For the two other positions, we have selected the following player with the highest score (for CB Hiriam Mier and for CDM Carlos Peña).
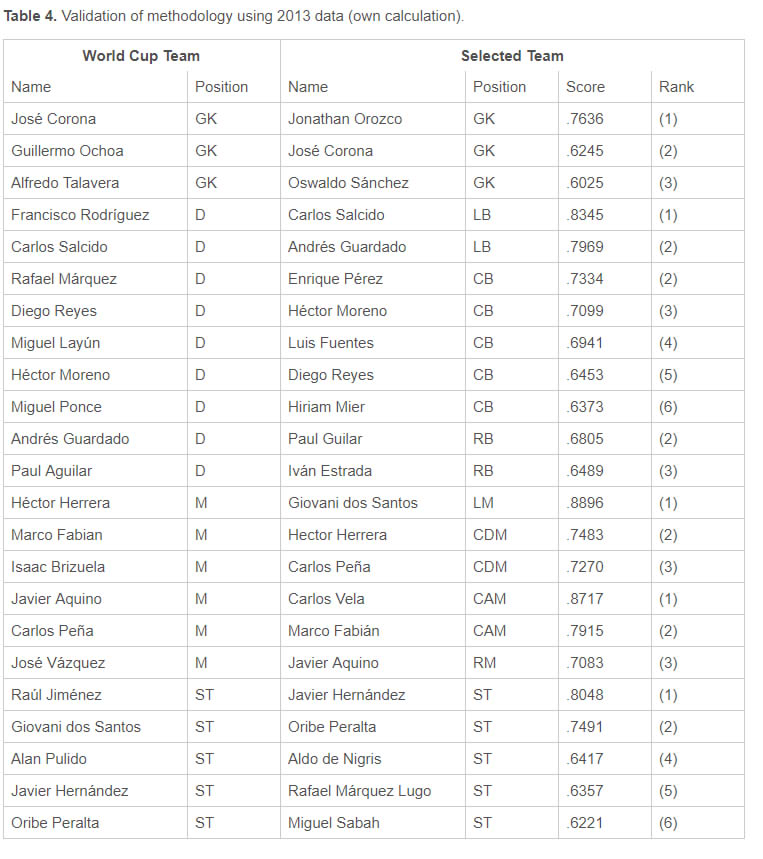 |
Validation of methodology using 2013 data (own calculation). |
Results
In this section, we present the results of the selection of the Mexican team for the 2018 FIFA World Cup in Russia. The selection is based on SoFIFA data published in August 2017, as well as the experts’ selection of the eight most important attributes for each position. The selection of the players is based on the same principles as in it was made in the validation. Furthermore, we have included substitutes (for each position one), for a broader discussion on possible changes in the main selection.
The selected team based on the TOPSIS calculation is presented in Table 5. The average score of the whole selected team is .7176, which denotes a distance of 28.24% from a team of ideal players. Considering this threshold, only 11 players of the main team are evaluated above. In general, with a closer look, the above-evaluated players are in attacking positions (CAM, LM, RM) with an exception of defensive right backs. Players on these positions have great skills in each of the selected attribute, resulting in overall short distance from the ideal case. For example, in CAM position the first three players (two in the main team and one substitute) are ranked highly above the average (.8490). Thus, the head coach of the Mexican team has high variability in selecting a player for a CAM.
On the other hand, the CB position might be seen as problematic as all the selected players are below the team average (.6164 for the main team, .6104 including the substitute player). There is no a player who surpasses his teammates in most of the attributes selected by the experts. As the differences between the players are not big, each player can excel in 1-2 attributes, whereas can be average in the rest of the attributes. Nevertheless, the below-average result for CBs can also be seen positively as the defense is not greatly depended on only one player. This might be the case of LB position where Héctor Moreno is the evident number one option (.7634) compare to Luis Fuentes (.6718). It is correct to say that the first option for the LB position was Miguel Layún (.7820). However, Miguel Layún better fits to RB position (.8665) for which he should be kept.
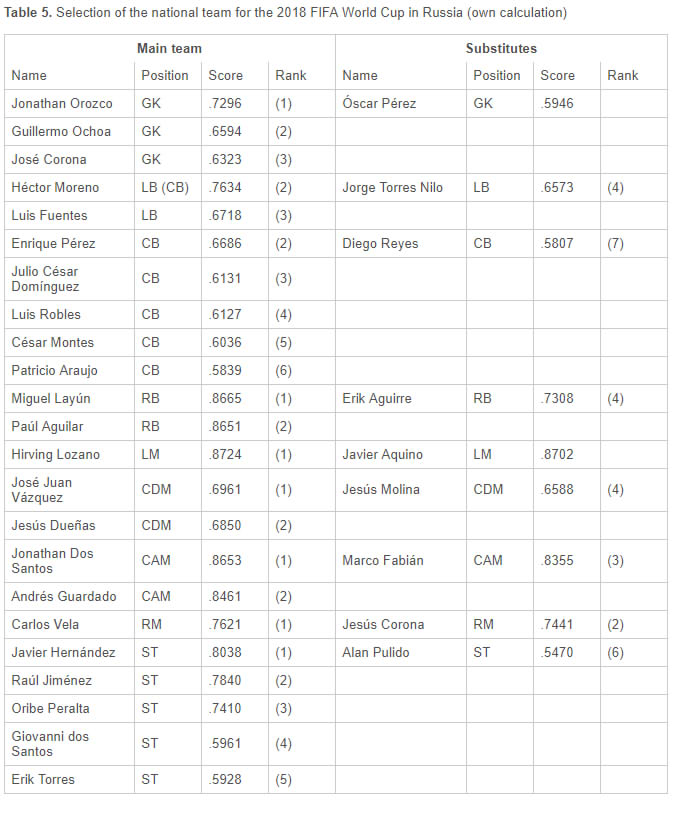 |
Selection of the national team for the 2018 FIFA World Cup in Russia (own calculation) |
It is evident that there is variability to occupy all positions, which makes the selection a complex (loose coupling organization). As a result, the head coach has distinct variability within the selected team for all positions. Table 6 shows the variability (universality) of players and how well each player fits to a particular position. For example, Jesús Dueñas can play in RB (.7669), CDM (.6850) and CM (.6627) position and in each one evaluated around the team’s average. This variability is desirable as the team’s formation changes regarding the opponent team, as well as regarding a phase of a game. In some cases, the variability is only in a theoretical perspective. For example, Patricio Araujo can play as CB (.5839), as well as CDM (.2648) and CAM (.2094). However, the evaluation of Patricio Araujo in the latter ones are significantly below the positions average (.6905, .8557 respectively). There are four better players for CDM position and five for the CAM position in the selection. We can see this theoretical variability in the case of Jonathan dos Santos for right midfielder position (.5724) and Giovanni dos Santos for striker position (.5961). In both cases, the difference between the best fit position and the alternative position is significant.
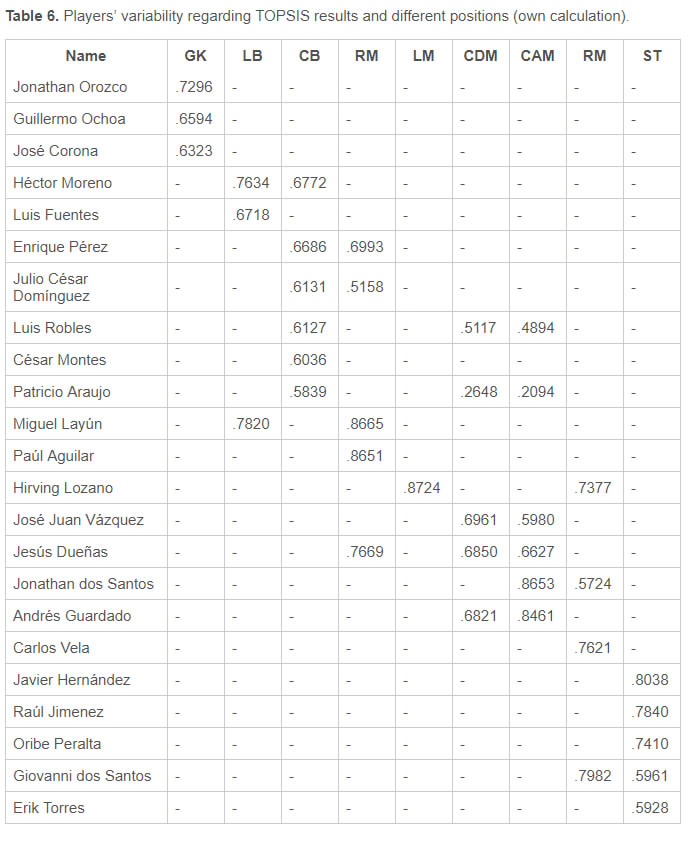 |
Selection of the national team for the 2018 FIFA World Cup in Russia (own calculation) |
Discussion
The process of players selection can be seen as a problem of a complex organization that includes many diffuse, vague, ambiguous, undefined, and even contradictory variables. Methods of operations research (Tavana et al., 2013; Sierksma, 2003; Ahmed, Deb and Jindal, 2013) and decision-making theory (Huang, Lin and Hu, 2015; Kamble et al., 2011; Ozceylan, 2016; Qader et al., 2017; Dadelo et al., 2014) are extensively used to support this process.
Common result of this selection is a list of players best-fit to a particular position. Then the team quality is presented as a sum of individual player’s capabilities (qualities). However, these models do not consider the interrelationships between players; in this article, we address this problem by retaking the organizational theories of ambiguity, pointing out that individual members have preferences and expectations that affect their performance; the sum of the individual behaviors affects the decisions of the organization, but this sum is not linear; the environment affects the form of decisions.
Liemhetcharat and Veloso (2014) pointed out that single-agent capabilities may not be known up front, e.g., as in ad hoc teams, as well as that a team performance goes beyond single-agent capabilities and depends on the specific synergy among agents). This can be a case of the proposed analysis in this article. The analysis tends to propose options for the final selection. From this reason, and to address the problem of single-agent capabilities, we have included substitute players for each position, which can give higher freedom to the final selection process. The results should then be seen as support for the final decision-making.
Head coaches have the final decision regarding players’ selection. Thus, they must consider inter-relations in the team formation. A team full of the top players might not be successful if the chemistry between players does not work. In this case, coaches use their experience and intuitions, so a strictly quantitative process loses effectiveness. Giske et al. (2013) analyzed decision-making styles of elite and non-elite football coaches. The results show that coaches tend to be predominantly rational or intuitive in their decision-making style, with almost no evidence of the avoidant decision-making style. Moreover, expert coaches are characterized by greater use of intuition in their decision-making than the non-experts, due to their level of experience. However, this intuitive decision-making, which rely on feelings and impressions, can be less effective (Harren, 1979). Therefore, coaches need to find a balance between objective and subjective decisions. This balance can be found using the MCDA methods to structure the selection process.
The process we propose does not negate both perspectives (subjective and objective) nor superimpose one focus on another (qualitative and quantitative). Rather, the proposed process helps us to manage the ambiguous nature of complex organizations, advances the paradigm of complexity in the Administration, which allows to resize the relation of the subject with the object necessary to refresh the organizational understanding (Jiménez-Bandala, 2015).
For the post-analysis, i.e. how well a team has been selected, performance evaluation can be used. Comparative analysis of different team selections can justify whether the selection led to desirable outcomes. The comparative analysis can evaluate different levels, such as national teams (Flégl, 2014), league clubs’ (Carmichael, Thomas and Ward, 2000; Barros and Leach, 2006; García-Sánchez, 2007) or players’ performance analysis (Tiedemann, Francksen and Latacz-Lohmann, 2011). Moreover, the comparative analysis can evaluate specific aspects of a game. Boscá et al. (2009) assessed offensive and defensive aspects in Italian and Spanish football. The higher the productivity of a team is the easier can be justified the selection.
Team’s quality is considered as the main factor that influences teams’ performance. However, there are many other social, economic or demographic factors that have direct impact on the performance (Andrade Rosas and Flegl, 2019). Moreover, football results also depend on collective offensive and defensive behavior of each team (Vilar et al., 2013).
Other complex organizations that can also resort to this method would be the political parties when selecting their candidates to occupy positions by popular election, where it seems contradictory to reconcile knowledge and skills with popularity and prestige, as well as ethical values. The universities and the selection of researchers; hospitals in the selection and integration of highly specialized medical teams; the selection of religious ministers, etc.
Last but not least, this method could be incorporated into other equally ambiguous processes in an organization for example in the choice of suppliers (Boran, et.al., 2009; Lima, Osiro and Ribeiro, 2014), since it implies multiple variables (product quality, delivery time, payment terms) and multiple objectives (cost savings, payment flexibility) including subjective factors such as trust and good treatment.
Conclusion
In this article, we have proposed new methodology of personnel selection based on Multi-criteria Decision Analysis aiming to complex organizations. We incorporate qualitative and quantitative approaches into the process, recognizing subjective and objective perspectives of decision makers. The proposed methodology was demonstrated on the selection of the Mexican national football team for the 2018 World Cup in Russia. We have validated the methodology on the 2014 World Cup in Brazil using de ad-hoc data. The validation proposed 13 out of 23 players selected for the final national team (56.52% accordance). Although the accordance of both selections is a bit under 60%, the methodology has proved its usability and applicability. It is almost impossible to have 100% accordance as football continuously evolves and, consequently, the criteria importance is continuously changing.
Although we have demonstrated the usability of the methodology in football, it can easily be applied in different areas. For managerial sciences, it involves enriching the understanding of organizational phenomena from the paradigm of complexity, recognizing dualities chaos-order, loose-strict coupling, multiple rationalities, diverse articulations between levels of analysis and recurrent transdisciplinary dialogues.
Appendix
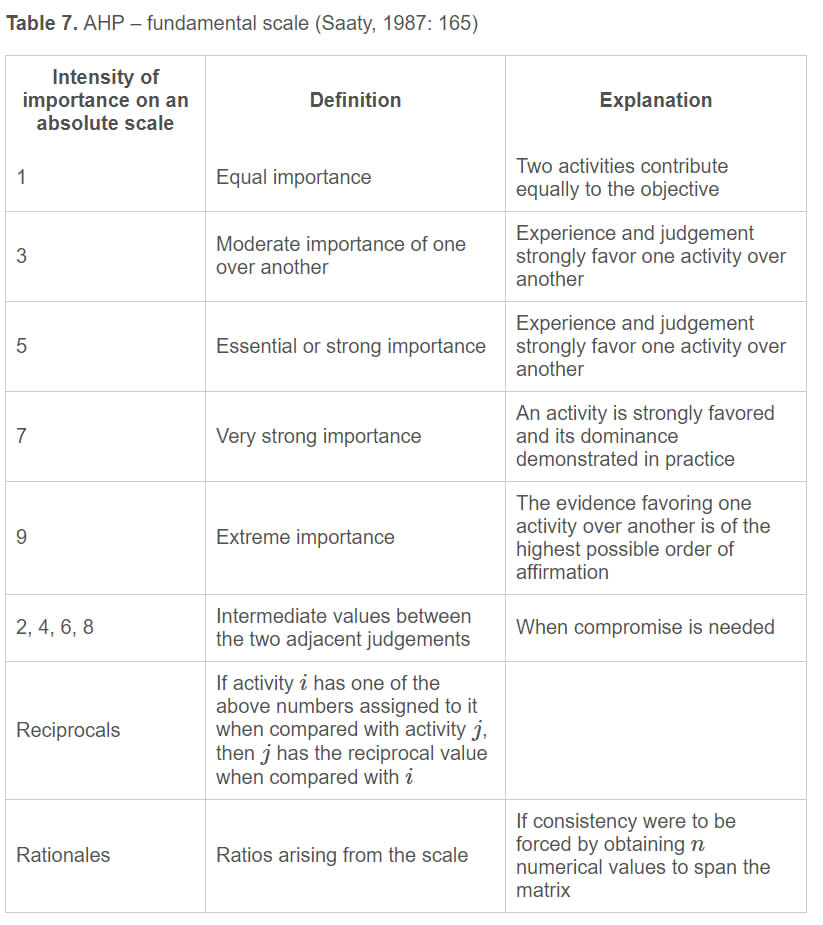 |
AHP – fundamental scale (Saaty, 1987: 165) |
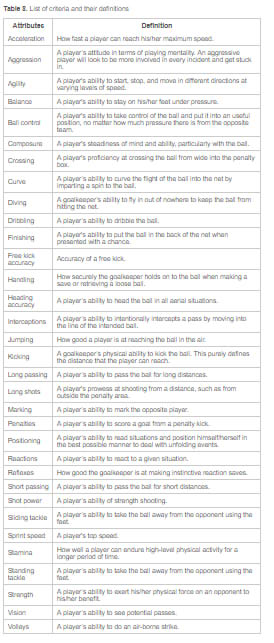 |
List of criteria and their definitions |
 |
Mexican national selection, November 2017 (Selección Mexicana de Fútbol, 2017) |