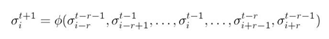
José Manuel Gómez Soto Investigador SNI, Nivel Candidato Universidad Autónoma de Zacatecas
E-mail: jmgomezgoo@gmail.com
Harold V McIntosh
Departamento de Aplicación de Microcomputadoras Instituto de Ciencias,
Universidad Autónoma de Puebla
Recibido: Agosto 17, 2010. Aceptado: Agosto 17, 2010
Resumen
La caracterización de las densidades de los autómatas celulares es un tema relevante en el estudio de estos modelos. Los autómatas celulares se han utilizado en muchas aplicaciones tales como la modelación de problemas de dinámica de fluidos, el estudio de materiales magnéticos en el procesamiento de imágenes, etcétera. Una caracterización de la densidad de estos autómatas permite realizar estudios matemáticos más profundos de los fenómenos que simulan. En este trabajo se propone caracterizar la densidad de los autómatas celulares unidimensionales con retardo utilizando los polinomios de densidad.
La caracterización de la densidad en estos autómatas celulares es importante ya que las transmisiones de señales con retardo están en muchos sistemas de la naturaleza. Entre ellos se encuentra la regularización del gen, las neuronas cerebrales y las señales en cascada en organismos multicelulares. Determinar entonces el comportamiento de la densidad en estos modelos nos dirá más acerca del fenómeno que se simula con ellos y acerca del modelo mismo, obtendremos más información sobre que tan robusto es el espacio temporal, cómo cambia su dinámica y cómo se afecta su capacidad de procesamiento de información.
Palabras clave: Autómata celular con retardos, caracterización de densidades, Polinomios de densidad.
Characterization of Densities in One-Dimensional Binary Cellular Automata with Delay Abstract
The characterization of the density of cellular automata is an important subject in the study of these models. Cellular automata have been used in many applications such as modeling of fluid dynamics problems; the study of magnetic materials in image processing, etcetera. A characterization of the density of these robots enables deeper mathematical study of simulating phenomena. In this work we characterize the density of one-dimensional cellular automata with delay using the density polynomials.
The characterization of these cellular automata density is important because signal transmission is delayed in many natural systems. Among them is the adjustment of the gene, brain cells and cascade signals in multicellular organisms. Then determining the behavior of the density in these models will tell us more about the phenomenon being simulated with and about the model itself. We get more information about how robust the temporary space is, how it changes its dynamics and how it affects their information processing ability.
Keywords: cellular automaton delays, characterization of density, density polynomials.
Introducción
Los autómatas celulares propuestos inicialmente por John von Neumann como un modelo para demostrar matemáticamente que las máquinas se pueden autoreproducir [1] han sido utilizados para modelar fenómenos que van desde la modelación de problemas de dinámica de fluidos [2–3], en el estudio de materiales magnéticos [4–5], en el procesamiento de imágenes [6], en el estudio de sistemas ecológicos [7–8], en robótica [9], en modelos de crecimiento mediante agregación por difusión limitada [10], en encriptamiento de información [11], en la propagación de virus o epidemias [12], en medios excitables [13], hasta la modelación de tráfico [14] y el crecimiento de las manchas urbanas [15]. A raíz de todas estas aplicaciones es deseable tener una formalización matemática de las propiedades de los autómatas celulares.
Dentro de esta formalización se encuentra determinar el comportamiento de las densidades. Un modelo de autómata celular propuesto para realizar estudios en sistemas donde existe un retardo en la transmisión de información se conoce como autómata celular con retados. Sobre estos autómatas celulares haremos la caracterización de las densidades mediante los polinomios de densidad. [16]
La caracterización de la densidad en estos autómatas celulares es importante ya que las transmisiones de señales con retardo están en muchos sistemas de la naturaleza. Entre ellos se encuentra la regularización del gen, las neuronas cerebrales y las señales en cascada en organismos multicelulares. Determinar entonces el comportamiento de la densidad en estos modelos no dirá más acerca del fenómeno que se simula con ellos y acerca del modelo mismo. Obtendremos más información sobre qué tan robusto es el espacio temporal de estos autómatas celulares, cómo cambia su dinámica y cómo se afecta su capacidad de procesamiento de información.
1. Autómatas celulares con retardos
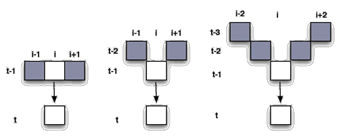
Dadas N células en un espacio unidimensional, donde cada cual está identificada de manera única mediante el índice i ∈ {0, 1,..., N−1}. Sea n << N el tamaño de la vecindad local, r = (n − 1)/2 el radio de dicha vecindad y el estado de la célula i. El tiempo es discreto y todas las células se actualizan en paralelo. Entonces el mapeo define la dinámica de la célula i de un autómata celular con retardo espacio temporal (Esto se ilustra también con la Figura 1).
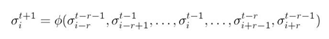

– 1. Panel de en medio: en un autómata celular con retardo y radio 1, el estado de la célula i depende del estado de la celda i en el tiempo t – 1 y de los estados de las células i − 1 e i + 1 en el tiempo t − 2. Panel derecho: en un autómata celular con retardo y radio = 2 es un autómata celular donde el estado de la célula i depende del estado de la célula i en el tiempo t – 1, de los estados de las células i – 1 e i + 1 en el tiempo t – 2 y de los estados de las células i – 2 e i + 2 en el tiempo t − 3.
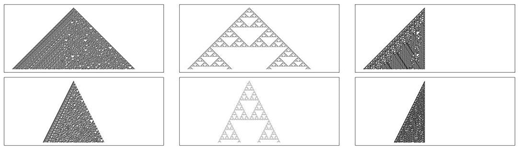
Ejemplos de los espacios fase de los autómatas celulares con retardos respecto de los convencionales se pueden apreciar en la Figura 2.
2. Polinomios de densidad en autómatas celulares con retardos
Al igual que en los autómatas celulares convencionales, el cálculo de los polinomios de densidad [16] se basa en la iteración de las funciones de densidad de preimágenes de los autómatas celulares:
Dada f(x) la función de densidad de preimágenes para cualquier conjunto de bloques de células; el comportamiento de la densidad del estado s se obtiene de manera iterativa mediante la orbita de x: x, f(x), f2(x), f (x)... donde x está dada por las vecindades que mapean en el estado s. A cada conjunto de preimágenes que se obtenga en cada generación se le aplicará la teoría del campo medio 1, para obtener el polinomio de cada generación.
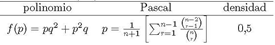
donde j = 1... |A| y es la delta de Kronecker es decir, = 1 si u = v y = 0 si
u ≠ v.
La función o polinomio que caracteriza el comportamiento de la densidad del estado s es la primer función de la serie que cumpla con para i ≥ 1. Dicho polinomio establece el comportamiento de las densidades del autómata celular y de manera indirecta indica la regla de evolución local que lo genera.
La diferencia en este proceso con respecto de los autómatas celulares convencionales radica en el cálculo de las preimágenes. En los autómatas celulares con retardos este cálculo consiste en encontrar las configuraciones de acuerdo con la estructura mostrada en Figura 3. Los ancestros de la primera generación se calculan en la configuración x1x2x3 que mapea en el estado 1. Para obtener las preimágenes de la segunda generación se calculan las configuraciones x’1x’2x’3x’4x’5x’6 donde x’1x’2x’6 x1, x’2x’3x’4 x2 y x’6x’4x’1 x’3. Y para obtener las preimágenes de la tercera generación se calculan las configuraciones x’’1x’’2x’’3x’’4x’’5x’’6x’’7x’’8x’’9x’’10x’’11x’’12x’’13x’’14x’’15, donde x’’1x’’2x’’12,
x’’1, x’’2x’’3x’’13, x’’2, x’’3x’’4x’’14, x’’3, x’’4x’’5x’’6 x’’4, x’’14x’’6x’’7
x’’5 y x’’15x’’7x’’8 x’’6. De esta manera se continua para las siguientes generaciones, manteniendo una convención de enumeración en forma de espiral1 hacia al centro1 como se ilustra también en la Figura 3.

Izquierda: primera generación. En medio: segunda generación.
3. Caso de estudio
Para ilustrar lo anterior calcularemos los polinomios de densidad que caracteriza el autómata celular con retardo 170. La regla local de esta regla está dada por {000, 010,
100, 110} → 0, {111, 101, 011, 001} → 1. De esta manera el estado 1 tiene las preimágenes {111, 101, 011, 001}. Si aplicamos esta regla a estos bloques,2 se obtienen los polinomios de densidad f(p) = p3+2p2q+pq2. Ahora se requiere calcular las
preimágenes de {111, 101, 011, 001}. Las preimágenes x′1x′2x′3x′4x′5x′6 para {111, 101,
011, 001} son {001011, 001111, 011011, 011111, 101011, 101111, 111011, 111111},
{001001, 001101, 011001, 011101, 101001, 101101, 111001, 111101}, {000011, 000111,
010011, 010111, 100011, 100111, 110011, 110111}, {000001, 000101, 010001, 010101,
100001, 100101, 110001, 110101} cuyo polinomio correspondiente es: f(p) = p6 + 5qp5+ 10q2p4+ 10q3p3+ 5q4p2+ q5p. Dado que los coeficientes que se presentan son
, coeficientes del triangulo de Pascal, usaremos la misma técnica empleada en [16] para demostrar convergencia y determinar la densidad en que se estabiliza el autómata celular, antes de continuar calculando preimágenes. Nótese que por la potencia del polinomio este pertenece al renglón n = 6 por lo que su relación con el triángulo de Pascal está dada por:
1 Es claro que puede haber muchas formas de realizar esta enumeración.
2 Este paso es equivalente a la teoría del campo medio.
a 1:![]()
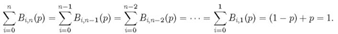
Ahora, dada la propiedad del triángulo que determina la suma cualquier renglón igual
Entonces la densidad del autómata celular está dada por:
![]()
Dado que
![]()
entonces
![]()
y
![]()
dividiendo 3 entre 4 se tiene:
![]()
Sustituyendo lo anterior en 2 tenemos:
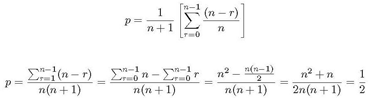
Por lo que el polinomio que puede caracterizar el comportamiento de este autómata celular con retardo con la regla 170, es el siguiente polinomio que converge densidad de 1/2:
f(p) = p6 + 5qp5 + 10q2p4 + 10q3p3 + 5q4p2 + q5p
4. Resultados
De las 88 reglas elementales fundamentales de los autómatas celulares con retado, al igual que en los autómatas celulares convencionales, las reglas que convergen en 0 en los autómatas celulares con retardo también lo hacen, a saber, las reglas 0, 8, 32, 40, 128, 160, 168. Y las reglas que mostraron convergencia en la familia de sus polinomios en los autómatas celulares convencionales también lo hacen en los autómatas celulares con retardo y, además, convergen en la misma densidad a pesar que las familias de los polinomios se encuentran en otros reglones con respecto de los convencionales.
Los autómatas celulares con retardo que convergen son:
Las reglas 10, 12, 34:
![]()
Las reglas 170, 184, 204:
![]()
Las reglas 2, 4:

Las reglas 15, 29, 51:

La regla 1:
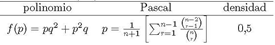
Las reglas 3, 5:

La regla 24:
Las reglas 76, 42:
![]()
La regla 138:
![]()
La regla 200:
![]()
El resto de las reglas se calcularon por el método de Montecarlo [16] obteniéndose las mismas aproximaciones que en los autómatas celulares convencionales.
5. Conclusiones
El único efecto que tienen los autómatas celulares con retardo r = 1 con respecto a los convencionales es que la evolución tiende a alargarse pero en términos de densidades el comportamiento se mantiene. Ello implica que las propiedades de computación universal de la regla 110 se mantienen en los autómatas celulares con retardo, teniendo así un dispositivo computacional con otro ciclo de tiempo. Lo mismo se puede concluir para las reglas con otras propiedades, como la regla 30, que genera números aleatorios. La cuestión a investigar en un futuro es si sucede lo mismo para los autómatas celulares con retardo en r = 2, r = 3,... r = n y por lo tanto sea posible tener las características del autómata celular en cualquier ciclo de tiempo.
Referencias
[1] Von Neumann, J. (1966). Theory of self-reproducing automata. (Editors by A. W. Burks), U.S.A.: University of Illinois Press, 388pp.
[2] Frisch, U.; Hasslacher, B. y Pomeau, Y. (1986). Lattice-Gas Automata for the Navier- Stokes Equation, Physics Review Letters, no. 56, U.S.A.: The American Physical Society, abril, pp. 1505-1508.
[3] Rothman, D. H. y Zaleski, S. (1997). Lattice–Gas Cellular Automata: Simple Models of Complex Hydrodinamics, Collection Alea Saclay: vol. 5, UK: Cambridge University Press, 320pp.
[4] Vichniac, G. Y. (1984). Simulating physics with cellular automata, Physica D: Nonlinear Phenomena, vol. 10, no. 1-2, UK. Elsevier, enero, pp. 96-116.
[5] Pomeau, Y. (1984). Invariant in cellular automata, Journal of Physics A. Mathematical and General, vol. 17, no. 8, UK. Elsevier, junio, pp. L415-L418.
[6] Kendall, P., Jr. y Michael J. B. Duff. (1984). Modern Cellular Automata: Theory and Applications, UK: Plenum Press, 364pp.
[7] Tilman, D. y Kareiva, P. (eds.). (1997). Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions, Monographs in Population Biology Vol. 30, New Jersey: Princeton University Press, 380pp.
[8] Gómez Soto, J. M. (2008). Computation of explicit preimages in one-dimensional cellular automata applying the De Bruijn Diagram. Journal of Cellular Automata, vol. 3, no. 3, Philadelphia: Old City Publishing, pp. 219-230.
[9] Butler, Z.; Kotay, K.; Rus, D. y Tomita, K. Cellular Automata for Descentralized Control of Self-Reconfigurable Robots, [En línea] Disponible en:
<http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.29.1204&rep=rep1&type= pdf>, consultado: agosto 2009.
[10] Spittle, J. A. y Brown, S. G. R. (1995). A Cellular Automaton Model of Steady-State Columnar-Dendritic Growth in Binary Alloys, Journal of Materials Science., vol. 30, no. 16, UK: Springer, pp. 3989-3994.
[11] Gutowitz, H. A. (1993). Cryptography with Dynamical Systems, en E. Goles y N. Boccara,(eds.) Cellular Automata and Cooperative Phenomena, Kluwer Academic Press.
[12] Fuks, H. y Lawniczak, A. T. (2001). Individual-based lattice model for spatial spread of epidemics, Discrete Dynamics in Nature and Society, vol. 6, no. 3, E.U.A.: Hindawi Publishing Corporation, pp. 191-200.
[13] Winfree, A. T. (1987). When Times Break Down: The Three-Dimensional Dynamics of Electronics Waves and Cardiac Arrhythmias. U.S.A.: Princeton University Press, 340pp.
[14] Boccara, N. y Fuks, H. (2000). Critical Behavior of a Cellular Automaton Highway Traffic Model, Journal of Physics A: Mathematical and general, vol. 33, no. 17, UK. Elsevier, pp. 3407-3415.
[15] Manrubia, S. C.; Zanette, D. H. y Solé, R. V. (1999). Transient Dynamics and Scaling Phenomena in Urban Growth. Fractals: Complex Geometry, Patterns and Scaling in Nature and Society, UK. World Scientific, vol. 7, no. 1, marzo, pp. 1-8.
[16] Gómez Soto, J. M.; McIntosh V., H. y Chapa Vergara, S. (s/a). Density Characterization in One-dimensional Cellular Automata. En preparación.
Bibliografía
Deutsch, A. y Dormann, S. (2004). Cellular Automata Modeling of Biological Pattern Formation. Boston: Birkhauser, 334pp.
Dresden, M. y Wong, M. (1975). Life Games and Statistical Models. Proceedings of the National Academy of Sciences. vol. 72, no. 3, E.U.A.: Stanford University Highwire Press, marzo, pp. 956-960. [En línea] Disponible en:
<http://www.pnas.org/content/72/3/956.full.pdf>, consultada: agosto de 2009.
Gutowitz, H. A. (1987). Local Structure Theory for Cellular Automata. Tesis de doctorado, E.U.A.: Rockefeller University.
Levin, S. A.; Powell, T. M. y Steele, J. H. (eds). (1983). Patch Dynamics. Lectures Notes in Biomathematics, Berlin: Springer Verlag.
Langton, C. G. (1990). Computation at the Edge of Chaos: Phase Transitions and Emergent Computation. Physica D: Nonlinear Phenomena, vol. 42, no. 1-3, UK. Elsevier, June, pp. 12-37.
Toffoli, T. y Margolus, N. (1987). Cellular Automata Machines. E.U.A.: The MIT Press, 259pp.
Wolfram, S. (1984). Universality and Complexity in Cellular Automata. Physica D: Nonlinear Phenomena, vol. 10, no. 1-2, UK. Elsevier, January, pp. 1-35.
Wolfram, S. (Ed.) (1986). Theory and Applications of Cellular Automata. Singapore: World Scientific Press, 570pp, ISBN 9971-50-124-4.